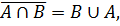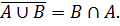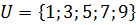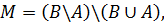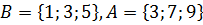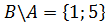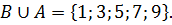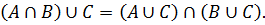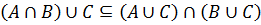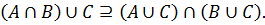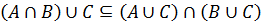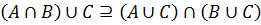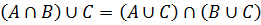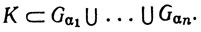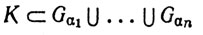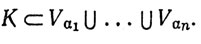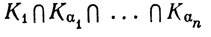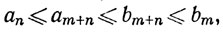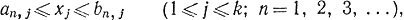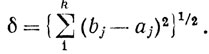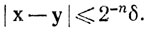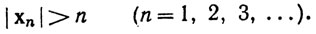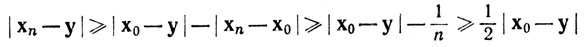Что такое семейство множеств

Топология (семейство множеств)

Смотреть что такое «Топология (семейство множеств)» в других словарях:

ЦЕНТРИРОВАННОЕ СЕМЕЙСТВО МНОЖЕСТВ — семейство, пересечение любого конечного множества элементов к рого не пусто. Напр., счетное семейство состоящее из подмножеств натурального ряда чисел вида центрировано. Центрированным будет любое семейство, пересечение всех элементов к рого не… … Математическая энциклопедия

ТОПОЛОГИЯ — в широком смысле область математики, изучающая топологич. свойства разл. матем. и физ. объектов. Интуитивно, к топологич. относятся качественные, устойчивые свойства, не меняющиеся при деформациях. Матем. формализация идеи о топологич. свойствах… … Физическая энциклопедия

Теория множеств — Теория множеств раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой… … Википедия

Относительная топология — Индуцированная или относительная топология в общей топологии это естественный способ задания топологии на подмножестве топологического пространства. Основная конструкция индуцированной топологии. Пусть X множество, и задано семейство отображений… … Википедия

ОПЕРАТОРНАЯ ТОПОЛОГИЯ — топология в пространстве L(E, F).непрерывных линейных отображений одного топологического векторного пространства Ев другое топологии, пространство F, превращающая пространство L(E, F).в топологическое векторное пространство. Пусть F локально… … Математическая энциклопедия

Дискетная топология — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия

Континуум (топология) — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия

Общая топология — Общая топология, или теоретико множественная топология раздел топологии, в котором изучаются понятия «непрерывности» и «предела» в наиболее общем смысле. Содержание 1 Область изучения 2 История 3 … Википедия

ЛОКАЛЬНО ВЫПУКЛАЯ ТОПОЛОГИЯ — такая (не обязательно отделимая) топология т на действительном или комплексном топологическом векторном пространстве Е, обладающая базисом из выпуклых окрестностей точек пространства Е, что линейные операции в Енепрерывны относительно топологии т … Математическая энциклопедия

Источник

Математика часто оперирует абстрактными объектами, для задания связи между которыми существуют различные операции, такие как пересечение и объединение множеств. Понятие множества является интуитивным, не определяемым. Оно обычно ассоциируется с набором чего-либо, группой каких-то предметов или живых объектов, совокупностью некоторых условий, рассматривается как класс, семейство в некоторой классификации, промежуток числовой прямой. Например, в геометрии рассматриваются линии как множества точек.

То, из чего состоит множество, называется его элементами.

Графическим изображением, служащим для наглядности рассматриваемых объектов, является круг Эйлера.

Что такое пересечение множеств

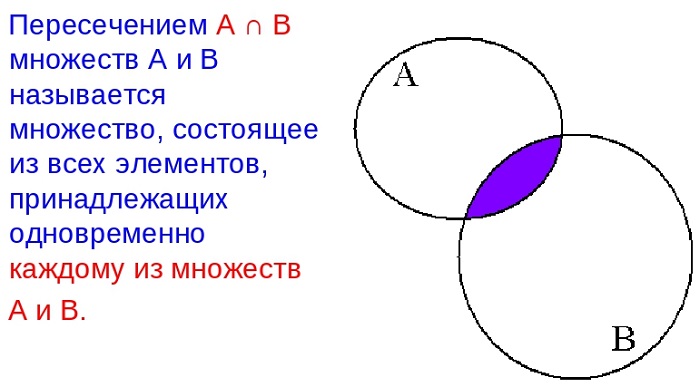
Для любого набора множеств их пересечением называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из заданных. Другими словами, это совокупность всех общих элементов.

С помощью кругов Эйлера-Венна пересечение можно изобразить так:

Часто применяется для определения решений систем уравнений и неравенств.

Ассоциируется с обычным умножением двух числовых объектов.

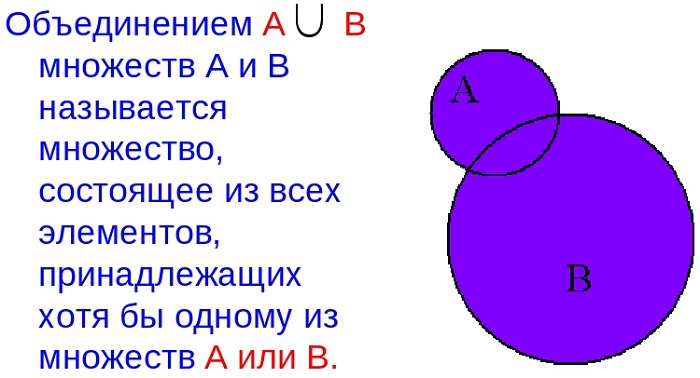
Что такое объединение множеств

Изображение кругами Эйлера выглядит следующим образом:

Часто используется при решении уравнений и неравенств, подчёркивая наличие серий корней и решений, нескольких используемых промежутков числовой прямой.

В обычной математике близко по смыслу с операцией, называемой «сложение».

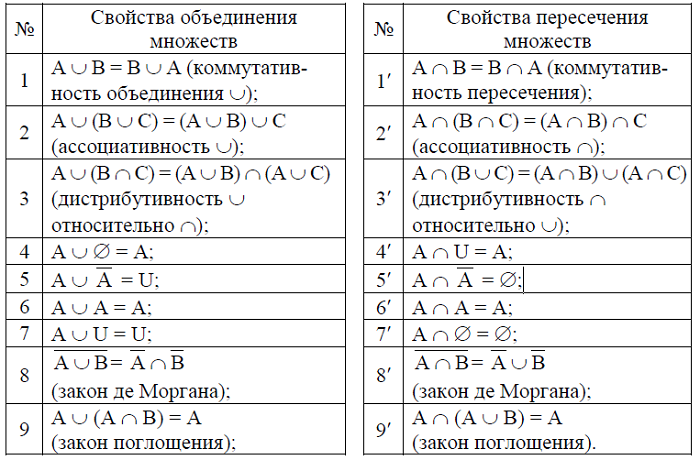
Свойства пересечения и объединения множеств

Для решения задач нужно знать о следующих свойствах:

1. Коммутативность (перестановочность):

Эти свойства распространяются на любое количество компонентов. Следуют из определения операций.

2. Ассоциативность (расстановка скобок):

Данные свойства также применимы к большому количеству компонентов. Позволяют опускать скобки и упрощать запись.

3. Дистрибутивность (раскрытие скобок):

(A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C);

(A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C).

4. Закон идемпотентности (идентичности):

Множество, не содержащее ни одного элемента, называется пустым. Обозначается перечёркнутым нулём: Ø

Выполнение операций с Ø:

Прослеживается аналог со сложением и умножением на ноль.

Операции над множествами

Помимо объединения и пересечения существуют другие операции:

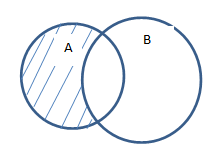
Для двух множеств A и B можно определить их разность как набор элементов, входящих в A и не содержащихся в B:

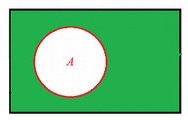
Рассматривая некоторое множество в качестве содержащего все остальные, можно прийти к понятию «дополнение», как к совокупности всех элементов, не входящих в A:

Благодаря этой операции свойства объединения и пересечения можно расширить/

Примеры решения задач

Задача №1

Выписать все элементы множества

При поиске M операции выполняются последовательно.

B \ A состоит из всех элементов B, которые не принадлежат A, поэтому:

B ∪ A включает в себя все элементы, принадлежащие хотя бы одному из множеств A или B. Таким образом:

M = (B \ A) \ (B ∪ A) состоит из всех элементов B \ A, которые не принадлежат B ∪ A, следовательно, M = Ø.

Задача №2

Доказать методом включений тождество:

Необходимо доказать выполнение включений:

Выбирается произвольный x из (A ∩ B) ∪ C. По определению операции объединения x ∈ B ∩ A или x ∈ C.

Если x ∈ B ∩ A, то по определению пересечения x ∈ B и x ∈ A.

Так как x ∈ A, то x ∈ C ∪ A; так как x ∈ B, то x ∈ C ∪ B, следовательно, x ∈ (A ∪ C) ∩ (B ∪ C).

Если x ∈ C, то x ∈ C ∪ A и x ∈ C ∪ B, а значит: x ∈ (A ∪ C) ∩ (B ∪ C).

Поскольку x ∈ (A ∩ B) ∪ C был выбран произвольно, утверждается, что любой элемент этого множества содержится в (A ∪ C) ∩ (B ∪ C), то есть:

Выбирается произвольный y из (A ∪ C) ∩ (B ∪ C).

По определению операции пересечения y ∈ C ∪ A и y ∈ C ∪ B.

Так как y ∈ C ∪ A, то y ∈ A или y ∈ C; так как y ∈ C ∪ B, то y ∈ C или y ∈ B. Таким образом, y ∈ C или y ∈ A и y ∈ B.

Если y ∈ A и y ∈ B, то y ∈ B ∩ A, а, следовательно, y ∈ (A ∩ B) ∪ C; если y ∈ C, то также y ∈ (A ∩ B) ∪ C.

Поскольку y из (A ∪ C) ∩ (B ∪ C) выбирался произвольно, утверждается, что любой элемент этого множества содержится в (A ∩ B) ∪ C, то есть

Из пунктов 1 и 2 вытекает, что

Источник

Теория множеств

Тео́рия мно́жеств — раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой математики. [источник не указан 479 дней]

Содержание

История

Наивная теория множеств

Первый набросок теории множеств принадлежит Бернарду Больцано («Парадоксы бесконечного», 1850). В этой работе рассматриваются произвольные (числовые) множества, и для их сравнения определено понятие взаимно-однозначного соответствия.

Программа Кантора вызвала резкие протесты со стороны многих современных ему крупных математиков. Особенно выделялся своим непримиримым к ней отношением Леопольд Кронекер, полагавший, что математическими объектами могут считаться лишь натуральные числа и то, что к ним непосредственно сводится (известна его фраза о том, что «бог создал натуральные числа, а всё прочее — дело рук человеческих»). Полностью отвергли теорию множеств и такие авторитетные математики, как Герман Шварц и Анри Пуанкаре. Тем не менее, другие крупные математики — в частности, Готлоб Фреге, Рихард Дедекинд и Давид Гильберт — поддержали Кантора в его намерении перевести всю математику на теоретико-множественный язык. В частности, теория множеств стала фундаментом теории меры и интеграла, топологии и функционального анализа.

Однако вскоре выяснилось, что установка Кантора на неограниченный произвол при оперировании с бесконечными множествами (выраженный им самим в принципе «сущность математики состоит в её свободе») является изначально порочной (см. Кризис математических основ). А именно, был обнаружен ряд теоретико-множественных антиномий: оказалось, что при использовании теоретико-множественных представлений некоторые утверждения могут быть доказаны вместе со своими отрицаниями (а тогда, согласно правилам классической логики высказываний, может быть «доказано» абсолютно любое утверждение).

После обнаружения антиномии Рассела часть математиков (например, Л. Э. Я. Брауэр и его школа) решила полностью отказаться от использования теоретико-множественных представлений. Другая же часть математиков, возглавленная Д. Гильбертом, предприняла ряд попыток строго обосновать ту часть теоретико-множественных представлений, которая казалась им наиболее ответственной за возникновение антиномий, на основе заведомо надёжной финитной математики. Логический аппарат усовершенствовал Бертран Рассел в работах, позднее собранных в его монографии «Начала математики» (1910—1913). В 1904—1908 гг. Эрнст Цермело предложил первую версию аксиоматической теории множеств.

Аксиоматическая теория множеств

Особенностью аксиоматического подхода является отказ от лежащего в основе программы Кантора представления о действительном существовании множеств в некотором идеальном мире. В рамках аксиоматических теорий множества «существуют» исключительно формальным образом, и их «свойства» могут существенно зависеть от выбора аксиоматики. Этот факт всегда являлся мишенью для критики со стороны тех математиков, которые не соглашались (как на том настаивал Гильберт) признать математику лишённой всякого содержания игрой в символы. В частности, Н. Н. Лузин писал, что «мощность континуума, если только мыслить его как множество точек, есть единая некая реальность», место которой в ряду кардинальных чисел не может зависеть от того, признаётся ли в качестве аксиомы континуум-гипотеза, или же её отрицание.

В настоящее время наиболее распространённой аксиоматической теорией множеств является ZFC — теория Цермело — Френкеля с аксиомой выбора. Вопрос о непротиворечивости этой теории (а тем более — о существовании модели для неё) остаётся нерешённым.

Не всеми математиками аксиома выбора принимается безоговорочно. Так, например Эмиль Борель и Анри Лебег считают, что доказательства, полученные при помощи этой аксиомы, имеют другую познавательную ценность, чем доказательства, независимые от неё. Другие же математики, такие как Феликс Хаусдорф и Адольф Френкель, принимают аксиому выбора безоговорочно, признавая за ней ту же степень очевидности, что и за другими аксиомами Цермело — Френкеля. [2]

Основные понятия

В основе теории множеств лежат первичные понятия: множество и отношение быть элементом множества (обозначается как [3] — «x есть элемент множества A», «x принадлежит множеству A»). Среди производных понятий наиболее важны следующие:

Для множеств определены следующие бинарные отношения:

Источник

Что такое семейство множеств

Компактные множества

2.31. Определение. Открытым покрытием множества Е в метрическом пространстве X мы будем называть семейство 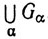α> открытых подмножеств пространства X, такое, что Е⊂.

2.32. Определение. Подмножество К метрического пространства X называется компактным, если каждое открытое покрытие множества К содержит конечное подпокрытие.

Понятие компактности имеет большое значение в анализе, особенно в связи с непрерывностью (гл. 4).

Ясно, что каждое конечное множество компактно. Существование широкого класса бесконечных компактных множеств в R k будет следовать из теоремы 2.41.

Мы заметили ранее (в п. 2.29), что если E⊂Y⊂X, то множество Е может быть открытым относительно Y, не будучи открытым относительно X. Свойство множества Е быть открытым зависит, таким образом, от пространства, в которое оно погружено. То же верно и в отношении свойства множества быть замкнутым.

2.33. Теорема.Допустим, что К⊂Y⊂X. Множество К компактно относительно X в том и только в том случае, когда оно компактно относительно Y.

В силу этой теоремы мы сможем во многих ситуациях рассматривать компактные множества как метрические пространства сами по себе, не обращая никакого внимания на объемлющее пространство. В частности, хотя почти бессмысленно говорить об открытых пространствах или о замкнутых пространствах (каждое метрическое пространство X служит открытым подмножеством самого себя и замкнутым подмножеством самого себя), имеет смысл говорить о компактных метрических пространствах.

Так как К⊂Y, то из (22) следует, что

Тем самым доказано, что множество К компактно относительно Y.

2.34. Теорема.Компактные подмножества метрических пространств замкнуты.

2.35. Теорема.Замкнутые подмножества компактных множеств компактны.

Следствие.Если F замкнуто, а К компактно, то F∩К компактно.

Доказательство. Теоремы 2.26 (b) и 2.34 показывают, что множество F∩K замкнуто, а так как F∩K⊂K, то по теореме 2.35 множество F∩K компактно.

пусто. Мы получили противоречие с услсзиями теоремы.

Доказательство. Если бы никакая точка множества К не была предельной точкой множества Е, то каждая точка q∈К имела бы окрестность V_q, содержащую не более одной точки множества Е (а именно точку q, если q∈E). Ясно, что никакое конечное подсемейство семейства q> не может покрыть множество Е;, то же верно и для К, так как Е⊂K. Но это противоречит компактности множества К.

и пусть I_n,j = [a_n,j, b_n,j]. При каждом j последовательность n,j> удовлетворяет предположениям теоремы 2.38. Значит, существуют вещественные числа x_j * (1≤j≤k), такие, что

2.40. Теорема.Любая k-мерная клетка компактна.

Доказательство. Пусть I есть k-мерная клетка, состоящая из всех точек x = (x₁. x_k), таких, что a_j≤j≤k. Положим

Тогда 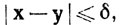если х∈I, у∈I.

Допустим, что вопреки утверждению теоремы существует открытое покрытие α> множества I, не содержащее конечного подпокрытия множества I. Положим c_j = (a_j + b_j) /₂ Сегменты [a_j, c_j] и [c_j, b_j] определяют тогда 2 k k-мерных клеток Q_i, объединение которых есть I. Хотя бы одно из этих множеств Q_i (обозначим его I₁) не может быть покрыто никаким конечным подсемейством семейства α> (в противном случае так была бы покрыта вся клетка I). Теперь мы разобьем I₁ и продолжим этот процесс. Мы получим последовательность n>, обладающую следующими свойствами:

(b) I_n не покрывается никаким конечным подсемейством семейства α>;

(c) если х∈I_n и y∈I_n, то

2.41. Теорема.Если множество Е из R k обладает одним из трех следующих свойств, то оно обладает и двумя другими:

(a) Е ограничено и замкнуто;

(с) каждое бесконечное подмножество множества Е имеет предельную точку, принадлежащую Е.

Если множество Е не ограничено, то оно содержит точки х_n, такие, что

Множество S, состоящее из этих точек х_n, бесконечно и, очевидно, не имеет предельных точек в R k и тем более в Е.

Таким образом, из (с) следует, что множество Е ограничено.

для всех n, за исключением некоторого конечного множества; это показывает, что у не является предельной точкой множества S (теорема 2.22).

Таким образом, S не имеет предельных точек в Е; значит, множество Е замкнуто, если выполнено (с).

Следует отметить в связи с этой теоремой, что (b) и (с) эквивалентны в любом метрическом пространстве (упражнение 13), но что из (а) в общем случае не следуют (b) и (с). Например, это так в пространстве 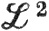, которое обсуждается в гл. 10. Один пример дается также в упражнении 9.

Источник

ДИСКРЕТНОЕ СЕМЕЙСТВО МНОЖЕСТВ

— семейство подмножеств Атопологич. пространства такое, что каждая точка пространства имеет окрестность, к-рая пересекает самое большее один элемент семейства А.

Смотреть что такое «ДИСКРЕТНОЕ СЕМЕЙСТВО МНОЖЕСТВ» в других словарях:

ЛОКАЛЬНО КОНЕЧНОЕ ПОКРЫТИЕ — покрытиетопологич. пространства его подмножествами такое, что у каждой точки есть окрестность, пересекающаяся лишь с конечным числом элементов этого покрытия. Не из всякого открытого покрытия прямой можно выделить Л. к. п.: достаточно рассмотреть … Математическая энциклопедия

Глоссарий общей топологии — Эта страница глоссарий. См. также основную статью: Общая топология В этом глоссарии приведены определения основных терминов, используемых в общей топологии. Курсивом выделены ссылки внутри глос … Википедия

Словарь терминов общей топологии — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч … Википедия

Дискетная топология — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия

Замкнутое отображение — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия

Замкнутое подмножество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия

Компонента связности — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия

Континуум (топология) — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия

Конус над топологическим пространством — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия

Локально стягиваемое пространство — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия

Источник