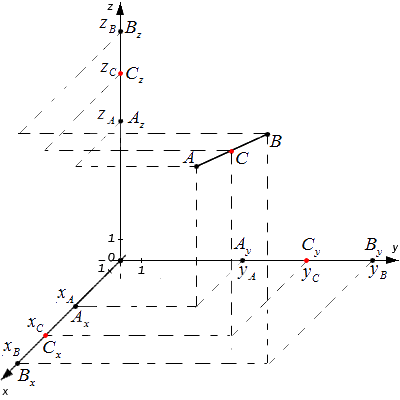
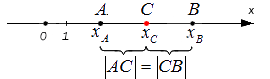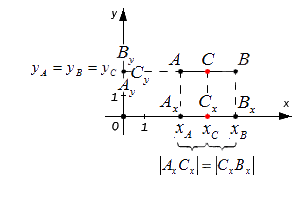Что такое середина отрезка может ли быть середина луча
Нахождение координат середины отрезка: примеры, решения
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
И далее мы рассмотрим, как же определять координаты середины отрезка (точки C ) при заданных координатах концов отрезка ( A и B ), расположенных на координатной прямой или в прямоугольной системе координат.
Середина отрезка на координатной прямой
Из первого равенства выведем формулу для координаты точки C : x C = x A + x B 2 (полусумма координат концов отрезка).
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
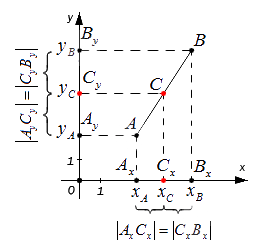
Середина отрезка на плоскости
x C = x A + x B 2 и y C = y A + y B 2
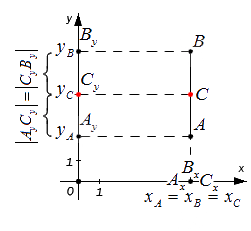
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Середина отрезка в пространстве
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Следовательно, точка C имеет координаты:
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Решение
Решение
Ответ: 58
Решение
Что такое середина отрезка
Ответ или решение 2
Определение координат середины отрезка
Определение середины отрезка графически
Для определение середины отрезка графически нужны:
Действия проводится в следующем порядке:
1) один конец циркуля с иглой устанавливается в любой конец отрезка;
2) раскрываем циркуль на расстояние визуально большее, чем половина отрезка и меньшее, чем весь отрезок;
3) проводим вторым концом циркуля с грифелем над отрезком дугу и под отрезком такую же дугу;
4) переносим иглу циркуля в другой конец отрезка;
5) вторым концом циркуля с грифелем над отрезком проводим дугу до пересечения с первой дугой над отрезком;
6) аналогично находим точку пересечения двух дуг под отрезком;
7) проводим через две полученные точки прямую;
8) точка пересечения исходного отрезка и проведенной прямой является серединой заданного отрезка.
Середина отрезка — это такая точка, которая делит отрезок (множество, которое состоит из двух точек, расположенных на прямой (концы отрезка), и точек, которые лежат между ними) на две равные части. Концы отрезка и его середину обычно обозначают латинскими буквами: A и B — концы, C — середина, C и D — концы, E — середина и т. д.
Зная координаты конца и начала отрезка, можно вычислить координаты его середины.
Пусть концы отрезка AB имеют координаты A (x₁; y₁) и B (x₂; y₂). Тогда координаты середины отрезка будут равны:
Зная координаты конца и начала отрезка, также можно вычислить расстояние, которое отделяет середину отрезка от его концов. Для этого необходимо вычислить длину отрезка по формуле:
Отрезок
Отрезок — это часть прямой, ограниченная двумя точками, лежащими на этой прямой. Точки, определяющие границы отрезка, называются концами отрезка.
Отрезок обозначается двумя большими латинскими буквами, поставленными при его концах: отрезок AB или BA.
Длина отрезка
Длина отрезка — это расстояние между концами отрезка. Любой отрезок имеет длину, бо́льшую нуля:
Измерение длины отрезка осуществляется путём сравнения данного отрезка с длиной единичного отрезка. Единичный отрезок — это отрезок, длина которого принимается за единицу. Следовательно:
длина отрезка – это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке.
Чаще всего используются единичные отрезки равные 1 мм, 1 см, 1 дм, 1 м или 1 км. Измерить длину отрезка можно линейкой или любым другим прибором для измерения длины:
Свойства длин отрезков:
Равные отрезки
Равные отрезки — это отрезки, имеющие одинаковую длину. Если наложить равные отрезки друг на друга, то их концы совпадут.
Пример. Возьмём два отрезка CD и LM:
Если расположить отрезки параллельно друг над другом так, чтобы точка C была над точкой L, то станет видно, что точка D располагается над точкой М:
Значит длины отрезков равны, следовательно CD = LM.
Сравнение отрезков
Сравнить два отрезка — это значит определить, равны они, или один больше другого.
Сравнить два отрезка можно, отложив на прямой оба отрезка из одной точки в одну и туже сторону. Для этого можно воспользоваться циркулем.
Чтобы отложить на прямой отрезок равный данному, сначала помещают ножки циркуля так, чтобы острия их концов упирались в концы отрезка, а затем, не изменяя раствора циркуля, переносят его так, чтобы оба его конца находились на прямой.
При сравнении двух отрезков возможно получение одного из представленных результатов: отрезки будут равны, первый отрезок будет больше второго или первый отрезок будет меньше второго.
Пример. Если отложить на прямой от любой точки, например C, в одну сторону два отрезка CA и CB и точка A окажется между точками C и B, то отрезок CA меньше отрезка CB (или CB больше отрезка CA):
Если точка B окажется между точками C и A, то отрезок CA больше отрезка CB (или CB меньше отрезка CA):
CA > CB или CB Пример. Сравнить длину отрезков AB и AC.
Так как отрезок AB имеет большую длину, чем отрезок AC, то
Так как отрезки AB и AC имеют одинаковую длину, то
Если при измерении отрезков их длины равны, то и отрезки равны.
Середина отрезка
Середина отрезка — это точка, делящая отрезок на две равные части.
Отрезок
Определение отрезка
Определение 1. Отрезок (или отрезок прямой )− это часть прямой, ограниченная двумя точками.
Определение 2. Отрезок − это множество, состоящая из двух различных точек данной прямой и всех точек, лежащих между ними.
Точки, ограничивающие отрезки называются концами отрезка, а точки, которые находятся между концами отрезка называются внутренними точками.
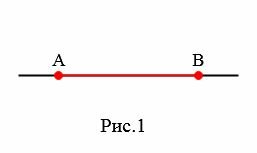 |
На рисунке 1 отрезок выделен красным цветом. Точки A и B концы отрезка, а точки между ними − внутренние точки.
Обозначение отрезков
Отрезки обозначаются с помощью его конечных точек. Отрезок на рисунке 1 обозначается так: AB или BA. Порядок следования имен конечных букв не имеет значения.
Сравнение отрезков
Для сравнения отрезков нужно:
Если два других конца совместяться, то отрезки равны. Если же конец одного отрезка находится внутри другого, то длина первого отрезка меньше второго.
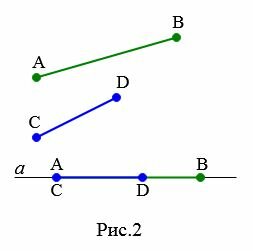 |
Пусть даны два отрезка AB и CD (Рис.2). Требуется сравнить эти отрезки, т.е. определить какой из них больше. Отложим эти отрезки на прямой a. Как видим, точка D находится внутри отрезка AB. Значит отрезок CD меньше отрезка AB. Это обозначается так: CD Определение 3. Точка отрезка,делящая его на два равных отрезка называется серединой отрезка.
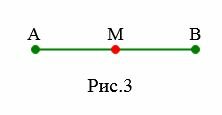 |
На рисунке 3 \( \small M \) является серединой отрезка \( \small AB \) поскольку \( \small AM = MB \).
Длина отрезка
Для определения длины отрезка его нужно сравнить с другим отрезком, принятым за единицу измерения.
В качестве единицы измерения можно взять, например, сантиметр. В этом случае для определения длины отрезка узнают, сколько раз в данном отрезке укладывается сантиметр. Этот показатель и является длиной отрезка выраженная в сантиметрах. Если длина отрезка AB равна трем сантиметрам, то пишут AB=3см.
Если отрезок, принятый за единицу измерения не укладывается целое число раз в измеряемом отрезке, то его обычно делят на 10 равных частей и определяют сколько раз одна такая часть укладывается в остатке. Одна десятая часть сантиметра называется миллиметром. В итоге получаем длину отрезка в сантиметрах и миллиметрах.
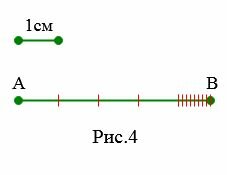 |
На Рис.4 1см укладывается в отрезке AB 4 раза и в остатке укладывается ровно 8 одну десятую часть сантиметра. Поэтому можно писать: AB=4см 8мм или AB=4.8см.
Направленный отрезок
Если для отрезка определить направление, то такой отрезок называется направленным отрезком. Направленный отрезок имеет начальную точку и конечную точку. В конечной точке направленного отрезка рисуют стрелку (Рис.5)
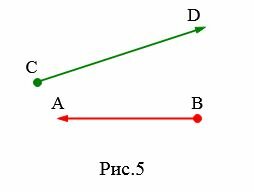 |
Для обозначения направленных отрезков сначала пишется начальная точка, а затем конечная точка. На рисунке 2 верхний направленный отрезок обозначают так: \( \small \overrightarrow
Как определить середину отрезка с помощью циркуля?
В этой статье вы узнаете, как разделить тот или иной отрезок с помощью такого инструмента, как циркуль. Ведь не всегда есть линейка под рукой. Такие знания пригодятся на практике.
Геометрия – это предмет, который изучается в школе и имеет применение на практике. Благодаря знаниям этого предмета можно узнать площадь, объем той или иной фигуры, или емкости, а также с легкостью разделить отрезок пополам с помощью сподручных инструментов. Узнаем дальше, как определить середину отрезка с помощью циркуля.
Как определить середину отрезка с помощью одного циркуля?
Интересно то, что определить середину отрезка с помощью циркуля можно и без линейки – это доказал еще в восемнадцатом веке итальянец Маскерони. Процесс построения сложнее, чем с помощью двух этих инструментов, но знания по этому поводу не помешают. Вначале определимся, что такое отрезок. Отрезком называют прямую, ограниченную двумя точками. И, чтобы найти середину отрезка, придется построить множество окружностей и найти множество точек их пересечения на них, пока не найдется середина отрезка.
ВАЖНО: Поиск середины отрезка сводится к нескольким шагам. Вначале отрезок следует удлинить ровно в два раза благодаря окружности большего диаметра, а потом рядом построений уже и найти саму точку отрезка, что делит его пополам.
Как построить середину отрезка с помощью циркуля и линейки?
Еще можно построить середину отрезка с помощью циркуля, линейки. Сделать это намного проще, чем в предыдущем варианте. Вам не понадобится рисовать множество окружностей разного диаметра, а достаточно построить лишь две одинаковые, а после провести перпендикуляр через точки пересечения с линиями окружности. Еще этот перпендикуляр называют серединным, что означает прямую, которую проводят под углом 90 градусов к отрезку.
Далее будет представлен мастер-класс на эту тему в подробностях и наглядно:
Итак, среднюю точку отрезка нашли, теперь еще и не помешает доказать, что именно CD – срединный перпендикуляр, и он делит отрезок пополам. Это сделать просто. Ведь две окружности, что образуют линию, имеют одинаковый радиус, диаметр. А у окружностей все точки на линии одинаково удалены от ее центра. Значит точки C и D также находятся на одинаковых расстояниях от точек A и B. Прямая которая соединяет точки D и C может быть лишь одна в плоскости. И точка пересечения на отрезке находится на одном и том же расстоянии. Все это и требовалось прояснить.