Что такое середина отрезка в геометрии 7 класс определение кратко

Отрезок

Отрезок — это часть прямой, ограниченная двумя точками, лежащими на этой прямой. Точки, определяющие границы отрезка, называются концами отрезка.

Отрезок обозначается двумя большими латинскими буквами, поставленными при его концах: отрезок AB или BA.

Длина отрезка

Длина отрезка — это расстояние между концами отрезка. Любой отрезок имеет длину, бо́льшую нуля:

Измерение длины отрезка осуществляется путём сравнения данного отрезка с длиной единичного отрезка. Единичный отрезок — это отрезок, длина которого принимается за единицу. Следовательно:

длина отрезка – это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке.

Чаще всего используются единичные отрезки равные 1 мм, 1 см, 1 дм, 1 м или 1 км. Измерить длину отрезка можно линейкой или любым другим прибором для измерения длины:

Свойства длин отрезков:

Равные отрезки

Равные отрезки — это отрезки, имеющие одинаковую длину. Если наложить равные отрезки друг на друга, то их концы совпадут.

Пример. Возьмём два отрезка CD и LM:

Если расположить отрезки параллельно друг над другом так, чтобы точка C была над точкой L, то станет видно, что точка D располагается над точкой М:

Значит длины отрезков равны, следовательно CD = LM.

Сравнение отрезков

Сравнить два отрезка — это значит определить, равны они, или один больше другого.

Сравнить два отрезка можно, отложив на прямой оба отрезка из одной точки в одну и туже сторону. Для этого можно воспользоваться циркулем.

Чтобы отложить на прямой отрезок равный данному, сначала помещают ножки циркуля так, чтобы острия их концов упирались в концы отрезка, а затем, не изменяя раствора циркуля, переносят его так, чтобы оба его конца находились на прямой.

При сравнении двух отрезков возможно получение одного из представленных результатов: отрезки будут равны, первый отрезок будет больше второго или первый отрезок будет меньше второго.

Пример. Если отложить на прямой от любой точки, например C, в одну сторону два отрезка CA и CB и точка A окажется между точками C и B, то отрезок CA меньше отрезка CB (или CB больше отрезка CA):

Если точка B окажется между точками C и A, то отрезок CA больше отрезка CB (или CB меньше отрезка CA):

CA > CB или CB Пример. Сравнить длину отрезков AB и AC.

Так как отрезок AB имеет большую длину, чем отрезок AC, то

Так как отрезки AB и AC имеют одинаковую длину, то

Если при измерении отрезков их длины равны, то и отрезки равны.

Середина отрезка

Середина отрезка — это точка, делящая отрезок на две равные части.

Источник

Отрезок

Определение отрезка

Определение 1. Отрезок (или отрезок прямой )− это часть прямой, ограниченная двумя точками.

Определение 2. Отрезок − это множество, состоящая из двух различных точек данной прямой и всех точек, лежащих между ними.

Точки, ограничивающие отрезки называются концами отрезка, а точки, которые находятся между концами отрезка называются внутренними точками.

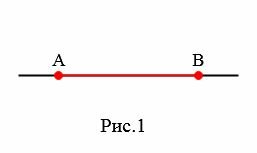На рисунке 1 отрезок выделен красным цветом. Точки A и B концы отрезка, а точки между ними − внутренние точки.

Обозначение отрезков

Отрезки обозначаются с помощью его конечных точек. Отрезок на рисунке 1 обозначается так: AB или BA. Порядок следования имен конечных букв не имеет значения.

Сравнение отрезков

Для сравнения отрезков нужно:

Если два других конца совместяться, то отрезки равны. Если же конец одного отрезка находится внутри другого, то длина первого отрезка меньше второго.

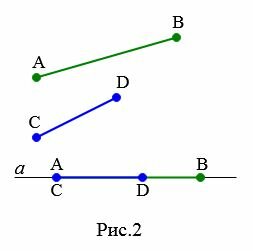Пусть даны два отрезка AB и CD (Рис.2). Требуется сравнить эти отрезки, т.е. определить какой из них больше. Отложим эти отрезки на прямой a. Как видим, точка D находится внутри отрезка AB. Значит отрезок CD меньше отрезка AB. Это обозначается так: CD Определение 3. Точка отрезка,делящая его на два равных отрезка называется серединой отрезка.

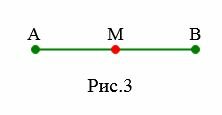На рисунке 3 \( \small M \) является серединой отрезка \( \small AB \) поскольку \( \small AM = MB \).

Длина отрезка

Для определения длины отрезка его нужно сравнить с другим отрезком, принятым за единицу измерения.

В качестве единицы измерения можно взять, например, сантиметр. В этом случае для определения длины отрезка узнают, сколько раз в данном отрезке укладывается сантиметр. Этот показатель и является длиной отрезка выраженная в сантиметрах. Если длина отрезка AB равна трем сантиметрам, то пишут AB=3см.

Если отрезок, принятый за единицу измерения не укладывается целое число раз в измеряемом отрезке, то его обычно делят на 10 равных частей и определяют сколько раз одна такая часть укладывается в остатке. Одна десятая часть сантиметра называется миллиметром. В итоге получаем длину отрезка в сантиметрах и миллиметрах.

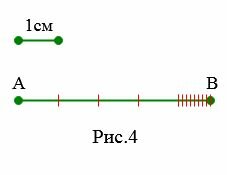На Рис.4 1см укладывается в отрезке AB 4 раза и в остатке укладывается ровно 8 одну десятую часть сантиметра. Поэтому можно писать: AB=4см 8мм или AB=4.8см.

Направленный отрезок

Если для отрезка определить направление, то такой отрезок называется направленным отрезком. Направленный отрезок имеет начальную точку и конечную точку. В конечной точке направленного отрезка рисуют стрелку (Рис.5)

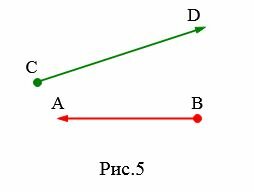Для обозначения направленных отрезков сначала пишется начальная точка, а затем конечная точка. На рисунке 2 верхний направленный отрезок обозначают так: \( \small \overrightarrow \) а нижний отрезок так: \( \small \overrightarrow \) Направленный отрезок называют вектором.

Источник

Что такое середина отрезка

Ответ или решение 2

Определение координат середины отрезка

Определение середины отрезка графически

Для определение середины отрезка графически нужны:

Действия проводится в следующем порядке:

1) один конец циркуля с иглой устанавливается в любой конец отрезка;

2) раскрываем циркуль на расстояние визуально большее, чем половина отрезка и меньшее, чем весь отрезок;

3) проводим вторым концом циркуля с грифелем над отрезком дугу и под отрезком такую же дугу;

4) переносим иглу циркуля в другой конец отрезка;

5) вторым концом циркуля с грифелем над отрезком проводим дугу до пересечения с первой дугой над отрезком;

6) аналогично находим точку пересечения двух дуг под отрезком;

7) проводим через две полученные точки прямую;

8) точка пересечения исходного отрезка и проведенной прямой является серединой заданного отрезка.

Середина отрезка — это такая точка, которая делит отрезок (множество, которое состоит из двух точек, расположенных на прямой (концы отрезка), и точек, которые лежат между ними) на две равные части. Концы отрезка и его середину обычно обозначают латинскими буквами: A и B — концы, C — середина, C и D — концы, E — середина и т. д.

Зная координаты конца и начала отрезка, можно вычислить координаты его середины.

Пусть концы отрезка AB имеют координаты A (x₁; y₁) и B (x₂; y₂). Тогда координаты середины отрезка будут равны:

Зная координаты конца и начала отрезка, также можно вычислить расстояние, которое отделяет середину отрезка от его концов. Для этого необходимо вычислить длину отрезка по формуле:

Источник

Термины, определения и формулы по геометрии за 7 класс

Геометрия – наука, занимающаяся изучением геометрических фигур (в переводе с греческого слово «геометрия» означает «землемерие»).

В планиметрии изучаются свойства фигур на плоскости. В стереометрии изучаются свойства фигур в пространстве.

Отрезок — это часть прямой, ограниченная двумя точками. Эти точки называются концами отрезка.

Угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.

Лучи называются сторонами угла, а точка — вершиной угла.

Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности.

Радиус окружности – отрезок, соединяющий центр окружности с какой-либо её точкой.

Отрезок, соединяющий две точки окружности, называется ее хордой.

Хорда, проходящая через центр окружности, называется диаметром.

Круг — это часть плоскости, ограниченная окружностью.

Угол называется развёрнутым, если обе его стороны лежат на одной прямой. ( Развёрнутый угол равен 180°).

Две геометрические фигуры называются равными, если их можно совместить наложением.

Середина отрезка — это точка отрезка, делящая его пополам, т.е. на два равных отрезка.

Биссектриса угла — это луч, исходящий из вершины угла и делящий его на два равных угла.

Угол называется прямым, если он равен 90°.

Угол называется острым, если он меньше 90° (т.е. меньше прямого угла).

Угол называется тупым, если он больше 90°, но меньше 180°. (т.е. больше прямого, но меньше развёрнутого).

Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными. Сумма смежных углов равна 180°.

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. Вертикальные углы равны.

Расстоянием от точки до прямой называется длина перпендикуляра, проведённого из этой точки к прямой.

Перпендикулярные прямые — прямые, которые при пересечении образуют прямой угол.

Параллельные прямые — прямые, лежащие в одной плоскости и не имеющие общих точек.

Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой и трех отрезков, соединяющих эти точки. Точки называются вершинами, а отрезки — сторонами треугольника.

Сумма углов треугольника равна 180°.

Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

Если все три угла треугольника острые, то треугольник называется остроугольным.

Если один из углов треугольника тупой, то треугольник называется тупоугольным.

Если один из углов треугольника прямой, то треугольник называется прямоугольным.

Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две стороны, образующие прямой угол — катетами.

(Т. о соотношениях между сторонами и углами треугольника) В треугольнике против большей стороны лежит больший угол, и обратно, против большего угла лежит большая сторона.

В прямоугольном треугольнике гипотенуза больше катета.

(Признак равнобедр. треугольника) Если два угла треугольника равны, то треугольник равнобедренный.

(Т. Неравенство треугольника) Каждая сторона треугольника меньше суммы двух других сторон.

Если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.

Теорема – утверждение, справедливость которого устанавливается путём рассуждений. Сами рассуждения называются доказательством теоремы.

Первый признак равенства треугольников

«Если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.»

Сокращенно его называют равенство «по двум сторонам и углу между ними».

На рисунке 1 представлен треугольник ABС. Который имеет три вершины (А, В и С). И стороны – АВ, АС и ВС.

Треугольники считаются равными, когда все их стороны и углы соответственно равны друг другу (в случае, когда равны лишь углы, а стороны пропорциональны, треугольники называются подобными). Таким образом очевидно, что равные треугольники можно наложить друг на друга – и они полностью совпадут.

Доказательство первого признака равенства треугольников

Два треугольника: ABC и DEF (рисунок 2).

По условию теоремы две пары отрезков этих треугольников равны между собой (АС = FD и СВ = EF). Углы между отрезками также равны (т.е. ∠АСВ = ∠EFD).

Доказать, что треугольник ABC равен треугольнику DEF.

Поскольку имеется равенство углов (∠АСВ = ∠EFD), треугольники можно наложить друг на друга, так чтобы вершина С совпадала с вершиной F.
При этом отрезки СА и СВ наложатся на отрезки FE и FD.
А поскольку отрезки двух треугольников равны между собой (АС = FD и СВ = EF по условию), то отрезок АВ также совпадёт со стороной ED.
Это в свою очередь даст совмещение вершин А и D, В и Е.
Следовательно, треугольники полностью совместятся, а значит, они равны.
Теорема доказана.

Второй признак равенства треугольников

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Как и в доказательстве первого признака, нужно убедиться, достаточно ли этого для равенства треугольников, можно ли их полностью совместить?

1. Так как MN=PR, то эти отрезки совмещаются, если совместить их конечные точки.

2. Так как∡N=∡R и∡M=∡P, то лучи MK и NK наложатся соответственно на лучи PT и RT.

3. Если совпадают лучи, то совпадают точки их пересечения K и T.

4. Совмещены все вершины треугольников, то есть ΔMNK и ΔPRT полностью совместятся, значит они равны.

Третий признак равенства треугольников

Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.

Опять попробуем совместить треугольникиΔMNK и ΔPRT наложением и убедится, что соответственно равные стороны гарантирует и равенство соответственных углов этих треугольников и они полностью совпадут.

Совместим, например, одинаковые отрезки MK иPT. Допустим, что точки N и R при этом не совмещаются.

Пусть O — середина отрезка NR. Соответственно данной информацииMN=PR, KN=TR. Треугольники MNR и KNR равнобедренные с общим основанием NR.

Поэтому их медианы MO и KO являются высотами, значит перпендикулярны NR. Прямые MO и KO не совпадают, так как точки M, K, O не лежат на одной прямой. Но через точку O прямой NR можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию.

Доказано, что должны совместиться и вершины N и R.

Третий признак позволяет назвать треугольник очень сильной, устойчивой фигурой, иногда говорят, что треугольник — жёсткая фигура. Если длины сторон не меняются, то углы тоже не меняются. Например, у четырёхугольника такого свойства нет. Поэтому разные поддержки и укрепления делают треугольными.

Перпендикуляр к прямой

Из точки не лежащей на прямой можно провести перпендикуляр к этой прямой и притом только один

Медианы,биссектриссы и высоты треугольника

В любом треугольнике медианы пересекаются в одной точке. Биссектрисы пересекаются в одной точке. Высоты или их продолжения также пересекаются в одной точке

Свойства равнобедренного треугольника

Признаки параллельности двух прямых. Теорема 1

Если при пересечении двух прямых секущей накрест лежащие углы равны то прямые параллельны.

Признаки параллельности прямых.Теорема 2

Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Признаки параллельности прямых. Теорема 3.

Если при пересечении двух прямых секущей сумма односторонних углов равна 180⁰ то прямые параллельны.

Теорема об углах образованных двумя параллельными прямыми и секущей.

Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

Аксиома параллельных прямых.

В одной плоскости с заданной прямой через точку, не лежащую на этой прямой, можно провести только одну прямую, параллельную заданной прямой.

Теоремы об углах, образованных двумя параллельными прямыми и секущей

Теорема Сумма углов треугольника равна 180°.

Рассмотрим произвольный треугольник KLM и докажем, что ∡K+∡L+∡M=180°.

Проведём через вершину L прямую a, параллельную стороне KM.

Углы, обозначенные 1, являются накрест лежащими углами при пересечении параллельных прямых a и KMсекущей KL, а углы, обозначенные 2 — накрест лежащими углами при пересечении тех же параллельных прямых секущей ML.

Очевидно, сумма углов 1, 2 и 3 равна развёрнутому углу с вершиной L, т. е.
∡1+∡2+∡3= 180°или ∡K+∡L+∡M=180°.

Следствия из теоремы о сумме углов треугольника

Следствие 1. Сумма острых углов прямоугольного треугольника равна 90°.

Следствие 2. В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.

Следствие 3. В равностороннем треугольнике каждый угол равен 60°.

Следствие 4. В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или прямой.

Следствие 5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Из равенств ∡KML+∡BML= 180° и ∡K+∡L+∡KML=180° получаем, что ∡BML=∡K+∡L.

Четырёхугольники

Многоугольник — фигура, состоящая из нескольких точек плоскости, поочередно соединённых между собой непересекающимися отрезками.

Выпуклый многоугольник — это многоугольник, который весь лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.

Теорема:Сумма внутренних углов выпуклого n-угольника равна (n-2)*1800.

Параллелограмм- это четырёхугольник, у которого противоположные стороны попарно параллельны.

Свойство:в параллелограмме противоположные стороны равны и противоположные углы равны.

Свойство:диагонали параллелограмма точкой пересечения делятся пополам.

Теорема(признакпараллелограмма): Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.

Теорема(признак параллелограмма): Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.

Теорема(признак параллелограмма): Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.

Трапеция — это четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.Параллельные стороны-основания, непараллельные стороны-боковые.

Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.

Прямоугольная трапеция — это трапеция, у которой один из углов прямой.

Теорема Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пресекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

Прямоугольник — это параллелограмм, у которого все углы прямые.

Свойство: диагонали прямоугольника равны.

Теорема(признакпрямоугольника): если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

Ромб — это параллелограмм, у которого все стороны равны.

Свойство: диагонали ромба взаимно перпендикулярны и делят его углы пополам.

Квадрат — это прямоугольник, у которого все стороны равны.

Площадь

Площадь плоской фигуры-это количество единичных квадратов, вмещающихся в данную фигуру.

Площадь квадрата равна квадрату его стороны.

Площадь прямоугольника равна произведению его смежных сторон.

Площадь параллелограмма равна произведению его основания на высоту.

Площадь треугольника равна половине произведения его основания на высоту.

Площадь прямоугольного треугольника равна произведению его катетов.

Если высоты двух треугольников равны, то их площади относятся как основания.

Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

Площадь трапеции равна полусумме её оснований на высоту.

Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Теорема(обр.): если квадрат одной стороны треугольника равен сумме квадратов двух других его сторон, то треугольник прямоугольный.

Подобные треугольники

Отрезки m и n пропорциональны отрезкам m1и n1,если отношения их длин равны m:m1= n: n1.

Подобные треугольники — это треугольники,у которых соответственные углы равны, а сходственные стороны пропорциональны.

Коэффициент подобия — это число, равное отношению сходственных сторон подобных треугольников.

Теорема: Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Свойство биссектрисы тр-ка: биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.

Теорема(первый признак подобия треугольников): если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

Теорема(второй признак подобия треугольников): если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.

Теорема(первый признак подобия треугольников): если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.

Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.

Теорема: Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

Среднее пропорциональное(среднее геометрическое)двух величин – это квадратный корень из произведения этих величин.

С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.

С. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы,заключённым между катетом и высотой, проведённой из вершины прямого угла.

Синус острого угла прямоугольного треугольника — это отношение противолежащего катета к гипотенузе.

Косинус острого угла прямоугольного треугольника- это отношение прилежащего катета к гипотенузе.

Окружность

Касательная к окружности – это прямая, имеющая с окружностью только одну общую точку.

Т. Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.

Т.(обр.) Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.

Центральный угол – это угол с вершиной в центре окружности.

Дуга окружности измеряется центральным углом, который на неё опирается.

Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность.

Т.Вписанный угол равен половине дуги, на которую он опирается.

С. Вписанные углы, опирающиеся на одну и ту же дугу, равны.

С. Вписанный угол, опирающийся на полуокружность, — прямой.

Т. Если две хорды окружности пересекаются, произведение отрезков одной хорды равно произведению отрезков другой хорды.

Источник