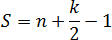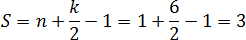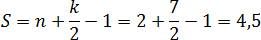Что такое сетка в математике
Метод узлов в задаче B5
Существует замечательная формула, которая позволяет считать площадь многоугольника на координатной сетке почти без ошибок. Это даже не формула, а настоящая теорема. На первый взгляд, она может показаться сложной. Но достаточно решить пару задач — и вы поймете, насколько это крутая фишка. Так что вперед!
Для начала введем новое определение:
— это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки.
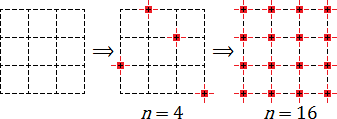
На первой картинке узлы вообще не обозначены. На второй обозначены 4 узла. Наконец, на третьей картинке обозначены все 16 узлов.
Какое отношение это имеет к задаче B5? Дело в том, что вершины многоугольника в таких задачах всегда лежат в узлах сетки. Как следствие, для них работает следующая теорема:
Теорема. Рассмотрим многоугольник на координатной сетке, вершины которого лежат в узлах этой сетки. Тогда площадь многоугольника равна:
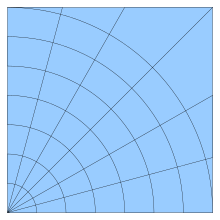
где n — число узлов внутри данного многоугольника, число узлов, которые лежат на его границе (граничных узлов).
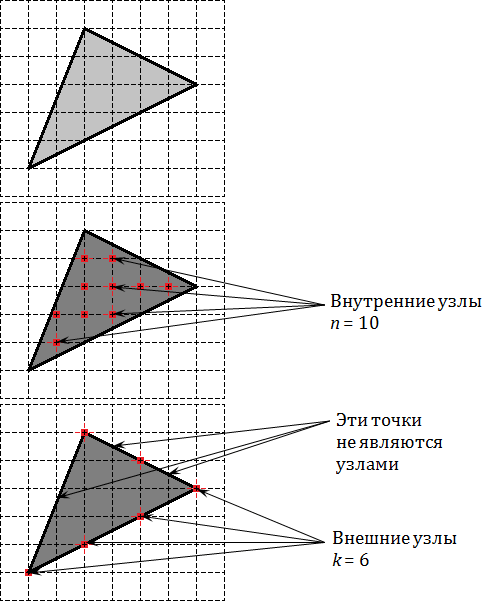
В качестве примера рассмотрим обычный треугольник на координатной сетке и попробуем отметить внутренние и граничные узлы.
На первой картинке дан обычный треугольник. На второй отмечены его внутренние узлы, число которых равно На третей картинке отмечены узлы лежащие на границе, их всего
Возможно, многим читателям непонятно, как считать числа Начните с внутренних узлов. Тут все очевидно: закрашиваем треугольник карандашом и смотрим, сколько узлов попало под закраску.
С граничными узлами чуть сложнее. Граница многоугольника — замкнутая ломаная, которая пересекает координатную сетку во многих точках. Проще всего отметить какую-нибудь «стартовую» точку, а затем обойти остальные.
Граничными узлами будут только те точки на ломаной, в которых одновременно пересекаются
Посмотрим, как все это работает в настоящих задачах.
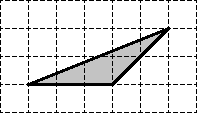
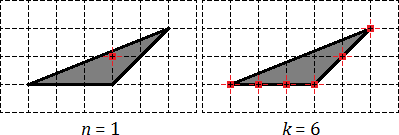
Задача. Найдите площадь треугольника, если размер клетки равен 1 x 1 см:
Для начала отметим узлы, которые лежат внутри треугольника, а также на его границе:
Получается, что внутренний узел всего один: Граничных узлов — целых шесть: три совпадают с вершинами треугольника, а еще три лежат на сторонах.
Теперь считаем площадь по формуле:
Вот и все! Задача решена.
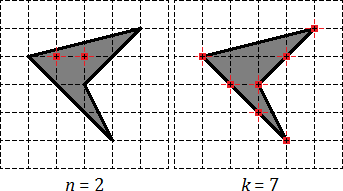
Задача. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см. Ответ дайте в квадратных сантиметрах.
Снова отмечаем внутренние и граничные узлы. Внутренних узлов всего Граничных узлов: из которых 4 являются вершинами четырехугольника, а еще 3 лежат на сторонах.
Остается подставить числа в формулу площади:
Обратите внимание на последний пример. Эту задачу реально предлагали на диагностической работе в 2012 году. Если работать по стандартной схеме, придется делать много дополнительных построений. А методом узлов все решается практически устно.
Важное замечание по площадям
Но формула — это еще не все. Давайте немного перепишем формулу, приведя слагаемые в правой части к общему знаменателю. Получим:
Числа n и k — это количество узлов, они всегда целые. Значит, весь числитель тоже целый. Мы делим его на 2, из чего следует важный факт:
Площадь всегда выражается целым числом или дробью. Причем в конце дроби всегда стоит «пять десятых»: 10,5; 17,5 и т.д.
Таким образом, площадь в задаче B5 всегда выражается целым числом или дробью Если ответ получается другим, значит, где-то допущена ошибка. Помните об этом, когда будете сдавать настоящий ЕГЭ по математике!
Сетка (геометрия)
Оглавление
Классификация
Сетки делятся на разные категории в зависимости от их топологии и геометрии. Принципиальное различие проводится между структурированными и неструктурированными сетками.
Текстурированная сетка
В случае структурированных сеток также возможны сложные структуры, в которых система сеток является регулярной, но в целом изогнутой или адаптированной к сложной геометрии. Также используются многоблочные структуры, в которых сетка формируется из нескольких структурированных блоков разного размера. Такие структурированные сетки могут быть созданы только частично автоматически.
В случае криволинейных сеток (англ. Curvilinear grids ) линии сетки задаются параметризованными кривыми. Однако термин довольно необычный. Тогда говорят просто о структурированных сетках.
Прямоугольные сетки (англ. Rectilinear grids ) полностью разделяют комнату на аксиально параллельные области, которые не обязательно должны быть одинакового размера. В трехмерном пространстве создаются кубоиды разного или одинакового размера.
Регулярная сетка (английский регулярная сетка ) полностью делит пространство на ось-параллельной прямоугольных участки, указанные кромки вдоль оси всегда имеют одинаковую длину.
Неструктурированная сетка
Неструктурированные сетки (англ. Unstructured grids ) не имеют заданной топологии и однородной геометрии ячеек сетки. Неструктурированные сети в основном являются результатом процесса адаптации. Известны также сетки из сложных ячеек, так называемые многогранные сетки. Структура ячеек здесь аналогична структуре мыльной пены.
Неструктурированные сетки можно очень гибко использовать, а также легко создавать автоматически. Однако управление данными сложнее, чем со структурированными сетками. С одной стороны, точки сетки не расположены в регулярном порядке, как в случае со структурированными сетками, а должны сохраняться индивидуально. С другой стороны, с самого начала неясно, какие ячейки примыкают к той или иной ячейке сетки. Эта информация о соседстве должна либо храниться явно при генерации сетки, либо она должна вычисляться сложным образом во время выполнения. Поэтому неструктурированные гриды обычно требуют многократных требований к памяти, чем структурированные гриды, и обычно вызывают более высокие вычислительные затраты.
Генерация сетки
Треугольная сетка
Адаптивные сетки
Также проводится различие между адаптивной и неадаптивной дискретизацией.
Неадаптивные решетки имеют одинаковое разрешение по всему объему. В случае небольших геометрических структур или областей с сильными изгибами, острыми углами или по-разному заданными параметрами материала грубая сетка с большими ячейками сетки больше не достаточна для дискретизации таких проблемных областей с достаточной точностью. Глобальное уточнение сетки в основном бесполезно из-за связанного с этим увеличения времени хранения и вычислений.
Здесь используется метод атаки на адаптивную генерацию сетки (англ. Adaptive meshing ), вот бы где еще ожидать отличных результатов, ошибка, сетка выбирает отлично. Это делается либо посредством априорного знания рассматриваемой проблемы, например, меньших элементов на поверхности компонентов или в сильно искривленных или тонких точках, либо с помощью методов, которые динамически уточняют, где ошибка велика, на основе заданных оценок ошибки. Последнее особенно важно в случае временных проблем, то есть, если проблемные области со временем меняют свое положение.
Приложения
технология
Геодезия
числовая математика
Эффективное построение сетки с использованием сеточных последовательностей
Замечали ли вы, что расчёт простой с виду модели иногда занимает много времени? Это может происходить из-за того, что автоматически созданная сетка содержит слишком много элементов. В таком случае бывает полезно переключиться c дефолтных на ручные настройки сетки (user-controlled mesh) для того, чтобы самостоятельно отредактировать сеточную последовательность в пакте COMSOL Multiphysics®. На одном из учебных примеров мы продемонстрируем все преимущества данного метода.
Выбор точной и эффективной сетки
Построение сетки — важный этап при моделировании, так как он напрямую определяет затраты вычислительных ресурсов при расчете. Более того, создание сетки — один из наиболее ресурсоёмких этапов при настройке и расчёте модели методом конечных элементов.
Как же правильно построить сетку для конкретной модели? Как правило, под этим выражением подразумевается выбор подходящего типа и размера конечных элементов. В COMSOL Multiphysics доступно четыре типа конечных элементов: тетраэдры, гексаэдры (параллелепипеды), треугольные призмы (призмы) и пирамиды. А также девять предустановленных размеров: от Очень мелкого (Extremely fine) до Очень крупного (Extremely coarse).

На рисунке изображены различные типы конечных элементов. Слева направо: тетраэдр, гексаэдр, треугольная призма и пирамида.
Как и другие доступные инструменты в COMSOL Multiphysics, построение сетки — очень гибкая и настраиваемая функция. Всего за насколько шагов вы легко построите сетку на каждой отдельной поверхности или каждом домене. По умолчанию автоматическая сетка с учетом физики (physics-controlled mesh) строится из конечных элементов разного типа и размера. Она может стать неплохой отправной точкой для изучения различных операций в построителе сеток и собственных модификаций путем добавления, перемещения, отключения и удаления узлов. Каждая операция выполняется последовательно согласно порядку, заданному в сеточной последовательности в узле Mesh (Сетка). Её настройка помогает уменьшить затраты на вычислительные ресурсы путём изменения числа, типа и размера конечных элементов. Эффективность и точность моделирования при этом сохраняется.
Настройка сеточной последовательности в COMSOL Multiphysics®
Теперь давайте разберём построение сетки на учебном примере электронного компонента, установленного на печатной плате с помощью шарикового припоя. Такой элемент может сильно нагреваться при длительной работе. Перегрев может как повредить устройство, так и создать опасность возгорания.
В данном примере длительное воздействие высокой температуры может привести к ползучести припоя, который удерживает компонент на плате. В конечном итоге это может деформации и разрушению соединения. Давайте же разберём на данном учебном примере, как настройка сетки может помочь нам в изучении такого устройства.
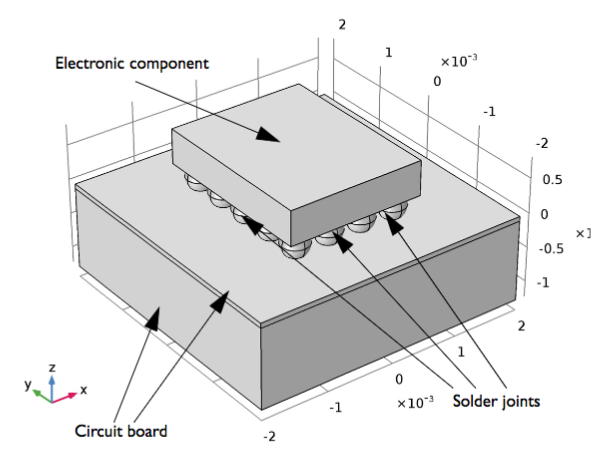
Электронный компонент, установленный на печатной плате с использованием шарикового припоя.
Для начала давайте автоматически построим сетку с учетом физики (physics-controlled mesh). По умолчанию — это произвольная тетраэдральная сетка. Размер конечного элемента устанавливается Нормальным (Normal), а сеточная последовательность, состоящая из узлов Размер (Size) и Произвольная тетраэдральная сетка (Free Tetrahedral), скрыта.
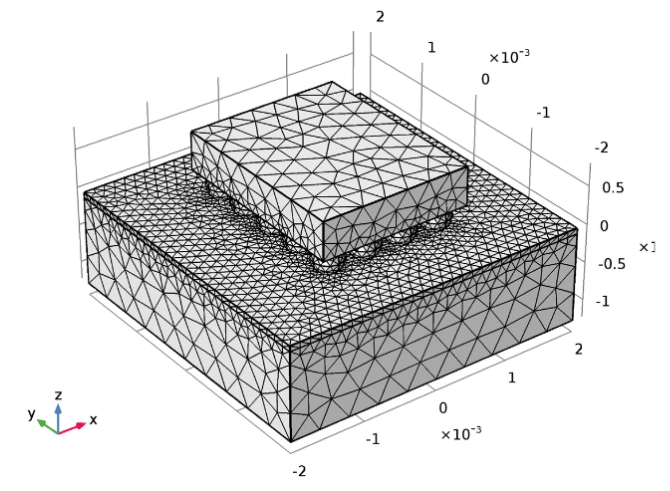
Построенная для электронного компонента сетка по умолчанию.
В результате автоматического построения сетки мы получаем 45000 элементов. В целом, это — неплохое конечно-элементное разбиение. Однако, при таком построении есть области, в которых сетка уж слишком измельчена. Для нашей задачи такая точность не нужна, к тому же, это будет приводить к дополнительным затратам на вычислительные ресурсы при моделировании. Сейчас мы покажем, как настройка сеточной последовательности может уменьшить количество элементов…
Использование локальных размеров и других сеточных операций при настройке сеточной последовательности
Чтобы уменьшить количество элементов, нужно настроить сетку так, чтобы она была более мелкой в местах соединения, то есть в областях шарикового припоя, и более крупной в других. Для этого давайте посмотрим на локальные и глобальные размеры в сеточной последовательности. По умолчанию параметры настройки первого глобального размера будут применяться ко всем элементам в узле Free Tetrahedral 1. Первый элемент сеточной последовательности мы называем глобальным размером (Size), так как он используется для всех последующих узлов по умолчанию, если они не переопределены. Мы же хотим задать свой размер конечных элементов.
Для этого щёлкаем правой кнопкой мыши по узлу Free Tetrahedral 1 и добавляем подузел с локальным размером элемента(Size). Он будет применяться для доменов с нашим шариковым припоем. С помощью такой настройки мы можем выделить именно те части геометрии, в которых нам необходимо получить самые точные результаты. Сделав эти нехитрые шаги, мы уже получаем 28000 конечных элементов, что почти в два раза меньше по сравнению с построенной изначально сеткой по умолчанию.
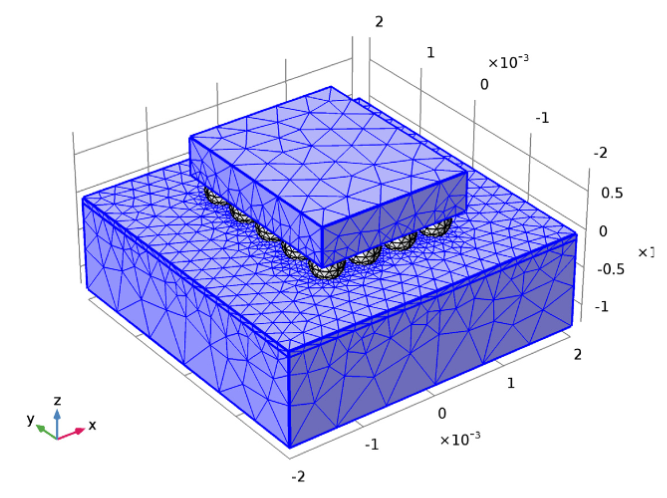
Настроенная сетка, с подробным разрешением только вокруг областей шарикового припоя.
Чтобы ещё больше сократить количество элементов, можно воспользоваться функцией протяжения сетки (Swept). Она поможет ещё немного упростить сетку и сократить вычислительные ресурсы. Применяем узел Free Tetrahedral 1 только к доменам, относящимся к шариковому припою. Теперь мы хотим использовать верхнюю границу печатной платы и нижнюю поверхность электронного компонента в качестве начальных плоскостей для протяжки. Важно отметить, что на некоторых областях этих граней уже построена сетка, так как они соприкасаются с шариковым припоем.
Добавляем узел Free Triangular (свободная треугольная сетка). Добавляя новые узлы в сеточную последовательность, можно переопределять сетку на необходимых нам доменах. Например, в данном случае будет использоваться сетка Free Tetrahedral 1 вместо Free Triangular 1. При желании этот порядок можно изменить, перемещая узлы в сеточной последовательности. Однако, в таком случае вам надо быть внимательнее и не допускать, чтобы узлы зависили от предыдущих операций. В ином случае программа может выдать ошибку.
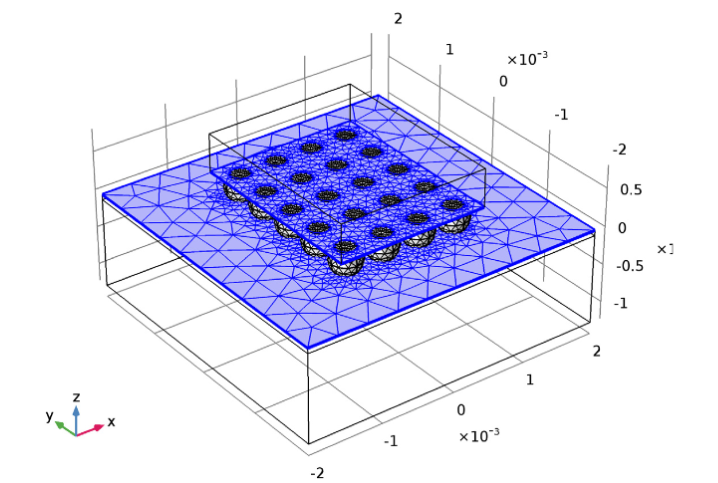
Построение Free Triangular 1сетки на верхней границе печатной платы и нижней поверхности электронного компонента.
Теперь давайте опять обратим внимание на локальные и глобальные размеры в сеточной последовательности. В добавленном узле Free Triangular 1 размер конечных элементов по умолчанию определился согласно первому глобальному размеру (Size). Нам это не подходит. Чтобы переопределить сетку, добавим в узел Free Triangular 1 подузел локальный размер и выберем тип Сoarser (крупная сетка). Построив сетку, мы увидим, что она такая же, как и предыдущая. Это произошло из-за того, что построитель сеток в COMSOL использовал ранее определённую сетку на краях шарикового припоя и глобальный размер для элементов (который мы задали Normal) на внешних границах. Поэтому подузел локальный размер применился только к внутренней области элементов.
Чтобы исправить эту неточность, нужно в первом глобальном размере (Size) поставить самую крупную сетку во всей геометрии. А затем уже можно добавлять локальные подузлы и выбирать более мелкие размеры конечных элементов. После этой настройки мы уже сможем переопределять размер элементов для функции Swept (сетка протяжкой) с помощью подузла Coarser. В результате получаем количество конечных элементов, равное примерно 17000.
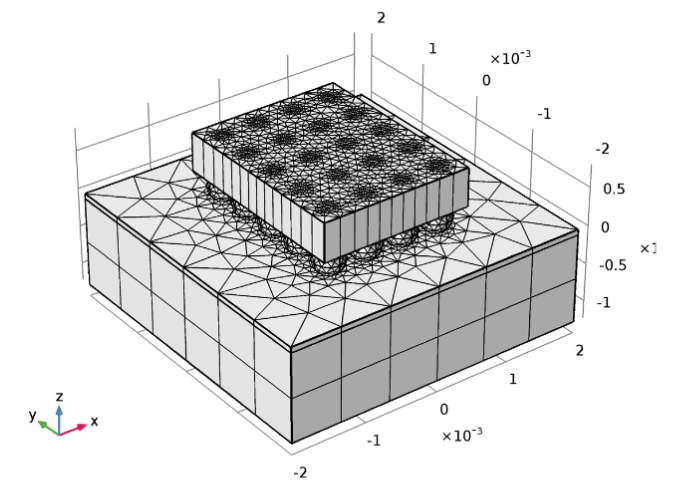
Построение ещё более измельчённой сетки с использованием функции протяжки.
Можно ещё более точно оптимизировать и донастроить сетку путём указания направления протяжки. Построив сетку таким образом, мы получили 21000 конечных элементов. В важных для нас областях, а именно — доменах с шариковым припоем, сетка была измельчена.
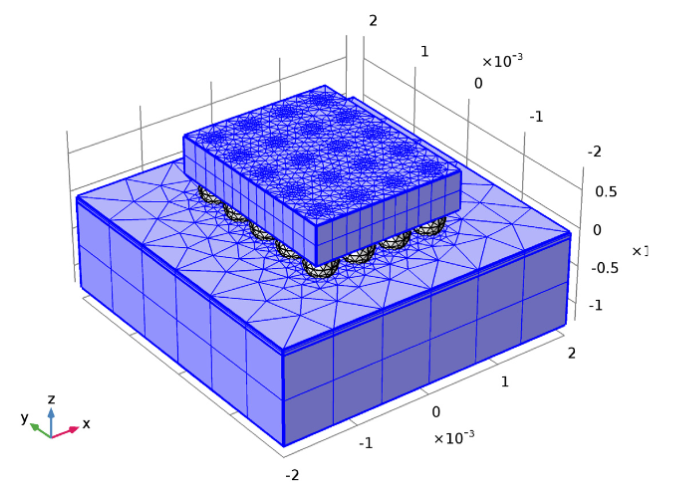
Измельчённая сетка в важных для расчета областях, при сохранении более крупного размера в остальных доменах.
Таким образом, можно сделать вывод о том, что настройка сеточной последовательности – это мощный инструмент при создании модели. Он позволяет уменьшить количество конечных элементов, оптимизировать затраты на вычислительные ресурсы и уменьшить время моделирования, сохраняя при этом точность результатов. Желаете узнать больше об эффективном построении сеток в COMSOL Multiphysics? Изучите дополнительные ресурсы по этой теме, пройдя по ссылкам ниже.
Теория графов. Основные понятия и виды графов
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Теория графов
В переводе с греческого граф — «пишу», «описываю». В современном мире граф описывает отношения. И наоборот: любое отношение можно описать в виде графа.
Теория графов — обширный раздел дискретной математики, в котором системно изучают свойства графов.
Теория графов широко применяется в решении экономических и управленческих задач, в программировании, химии, конструировании и изучении электрических цепей, коммуникации, психологии, социологии, лингвистике и в других областях.
Для чего строят графы: чтобы отобразить отношения на множествах. По сути, графы помогают визуально представить всяческие сложные взаимодействия: аэропорты и рейсы между ними, разные отделы в компании, молекулы в веществе.
Давайте на примере.
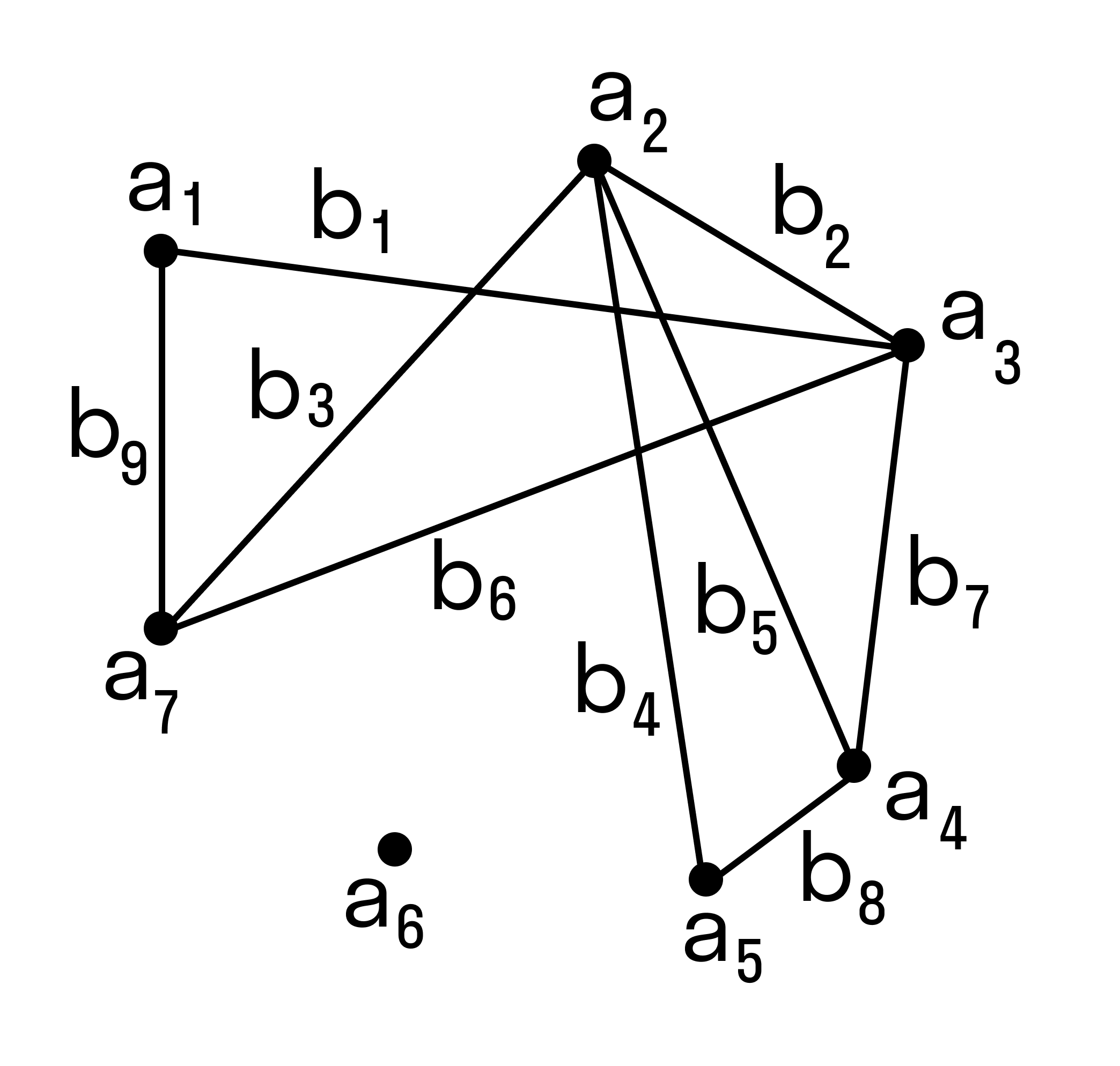
На множестве A зададим отношение знакомства между людьми из этого множества. Строим граф из точек и связок. Связки будут связывать пары людей, знакомых между собой.
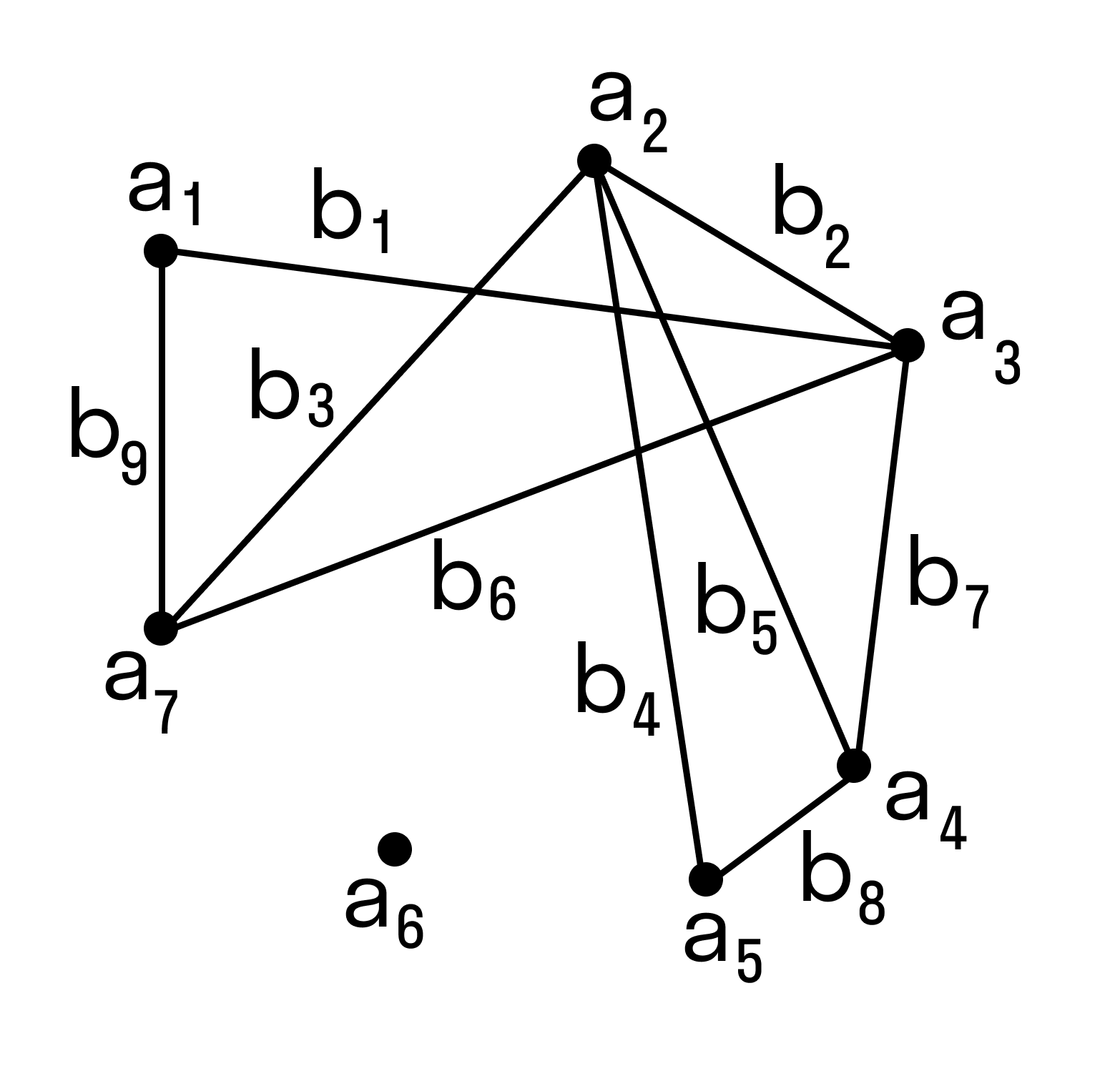
Число знакомых у одних людей может отличаться от числа знакомых у других людей, некоторые могут вовсе не быть знакомы (такие элементы будут точками, не соединёнными ни с какой другой). Так получился граф:
В данном случае точки — это вершины графа, а связки — рёбра графа.
Теория графов не учитывает конкретную природу множеств A и B. Существует большое количество разных задач, при решении которых можно временно забыть о содержании множеств и их элементов. Эта специфика не отражается на ходе решения задачи.
Например, вопрос в задаче стоит так: можно ли из точки A добраться до точки E, если двигаться только по соединяющим точки линиям. Когда задача решена, мы получаем решение, верное для любого содержания, которое можно смоделировать в виде графа.
Не удивительно, что теория графов — один из самых востребованных инструментов при создании искусственного интеллекта: ведь искусственный интеллект может обсудить с человеком вопросы отношений, географии или музыки, решения различных задач.
Графом называется система объектов произвольной природы (вершин) и связок (ребер), соединяющих некоторые пары этих объектов.
Пусть V — (непустое) множество вершин, элементы v ∈ V — вершины. Граф G = G(V) с множеством вершин V есть некоторое семейство пар вида: e = (a, b), где a, b ∈ V, указывающих, какие вершины остаются соединёнными. Каждая пара e = (a, b) — ребро графа. Множество U — множество ребер e графа. Вершины a и b — концевые точки ребра e.
Широкое применение теории графов в компьютерных науках и информационных технологиях можно объяснить понятием графа как структуры данных. В компьютерных науках и информационных технологиях граф можно описать, как нелинейную структуру данных.
Линейные структуры данных особенны тем, что связывают элементы отношениями по типу «простого соседства». Линейными структурами данных можно назвать массивы, таблицы, списки, очереди, стеки, строки. В нелинейных структурах данных элементы располагаются на различных уровнях иерархии и подразделяются на три вида: исходные, порожденные и подобные.
Основные понятия теории графов
Граф — это геометрическая фигура, которая состоит из точек и линий, которые их соединяют. Точки называют вершинами графа, а линии — ребрами.
Лемма о рукопожатиях
В любом графе сумма степеней всех вершин равна удвоенному числу ребер.
Доказательство леммы о рукопожатиях
Если ребро соединяет две различные вершины графа, то при подсчете суммы степеней вершин мы учтем это ребро дважды.
Если же ребро является петлей — при подсчете суммы степеней вершин мы также учтем его дважды (по определению степени вершины).
Из леммы о рукопожатиях следует: в любом графе число вершин нечетной степени — четно.
Пример 1. В классе 30 человек. Может ли быть так, что у 9 из них есть 3 друга в этом классе, у 11 — 4 друга, а у 10 — 5 друзей? Учесть, что дружбы взаимные.
Если бы это было возможно, то можно было бы нарисовать граф с 30 вершинами, 9 из которых имели бы степень 3, 11 — со степенью 4, 10 — со степенью 5. Однако у такого графа 19 нечетных вершин, что противоречит следствию из леммы о рукопожатиях.
Пример 2. Каждый из 102 учеников одной школы знаком не менее чем с 68 другими. Доказать, что среди них найдутся четверо ребят с одинаковым числом знакомых.
Сначала предположим противоположное. Тогда для каждого числа от 68 до 101 есть не более трех человек с таким числом знакомых. С другой стороны, у нас есть ровно 34 натуральных числа, начиная с 68 и заканчивая 101, а 102 = 34 * 3.
Это значит, что для каждого числа от 68 до 101 есть ровно три человека, имеющих такое число знакомых. Но тогда количество людей, имеющих нечетное число знакомых, нечетно. Противоречие.
Путь и цепь в графе
Путем или цепью в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.
Циклом называют путь, в котором первая и последняя вершины совпадают.
Путь или цикл называют простым, если ребра в нем не повторяются.
Если в графе любые две вершины соединены путем, то такой граф называется связным.
Можно рассмотреть такое подмножество вершин графа, что каждые две вершины этого подмножества соединены путем, а никакая другая вершина не соединена ни с какой вершиной этого подмножества.
Каждое такое подмножество, вместе со всеми ребрами исходного графа, соединяющими вершины этого подмножества, называется компонентой связности.
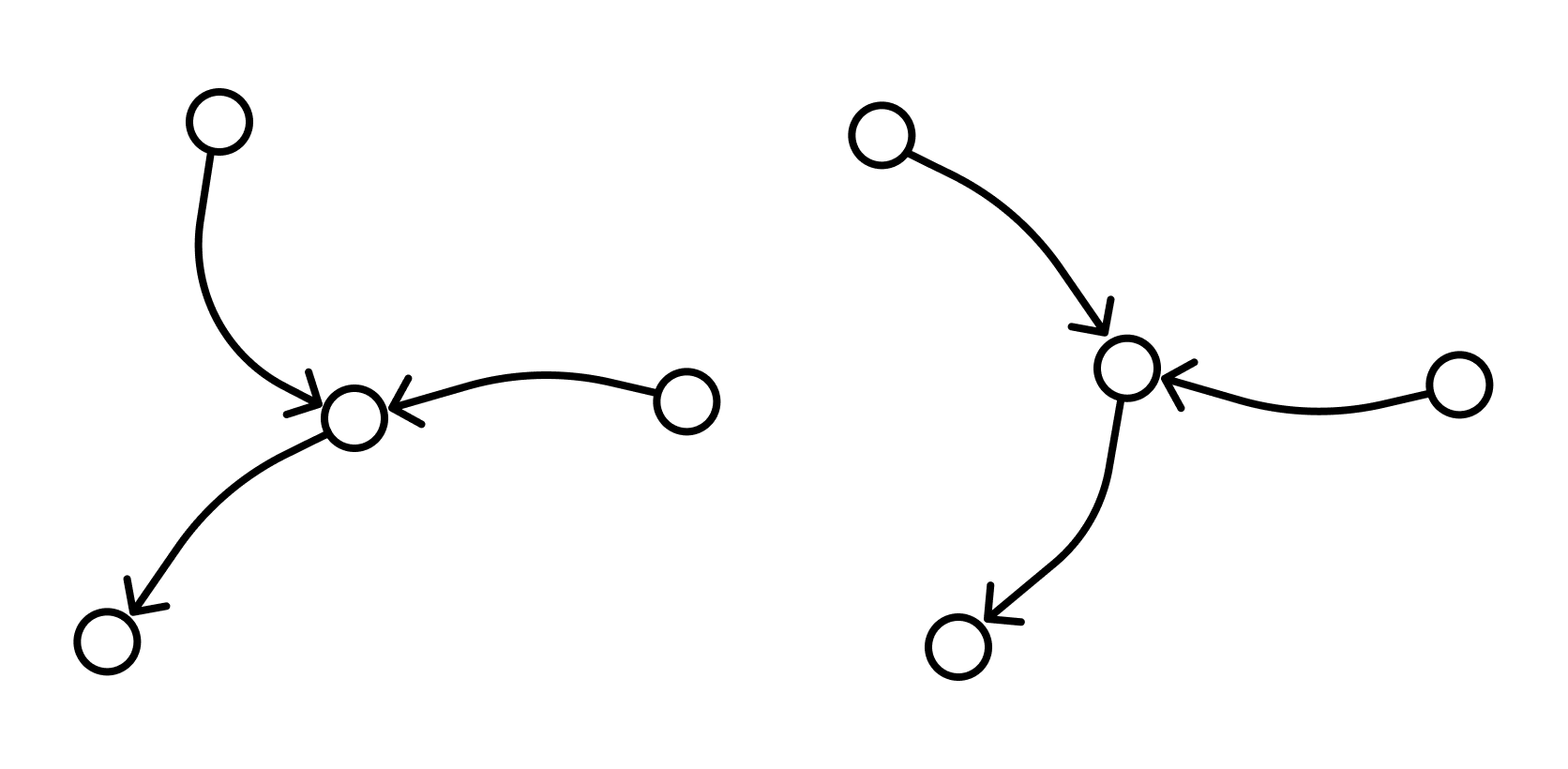
Один и тот же граф можно нарисовать разными способами. Вот, например, два изображения одного и того же графа, которые различаются кривизной:
Два графа называются изоморфными, если у них поровну вершин. При этом вершины каждого графа можно занумеровать числами так, чтобы вершины первого графа были соединены ребром тогда и только тогда, когда соединены ребром соответствующие занумерованные теми же числами вершины второго графа.
Граф H, множество вершин V’ которого является подмножеством вершин V данного графа G и множество рёбер которого является подмножеством рёбер графа G соединяющими вершины из V’ называется подграфом графа G.
Визуализация графовых моделей
Визуализация — это процесс преобразования больших и сложных видов абстрактной информации в интуитивно-понятную визуальную форму. Другими словами, когда мы рисуем то, что нам непонятно — и сразу все встает на свои места.
Графы — и есть помощники в этом деле. Они помогают представить любую информацию, которую можно промоделировать в виде объектов и связей между ними.
Граф можно нарисовать на плоскости или в трехмерном пространстве. Его можно изобразить целиком, частично или иерархически.
Изобразительное соглашение — одно из основных правил, которому должно удовлетворять изображение графа, чтобы быть допустимым. Например, при изображении блок-схемы программы можно использовать соглашение о том, что все вершины должны изображаться прямоугольниками, а дуги — ломаными линиями с вертикальными и горизонтальными звеньями. При этом, конкретный вид соглашения может быть достаточно сложен и включать много деталей.
Виды изобразительных соглашений:
Виды графов
Виды графов можно определять по тому, как их построили или по свойствам вершин или ребер.
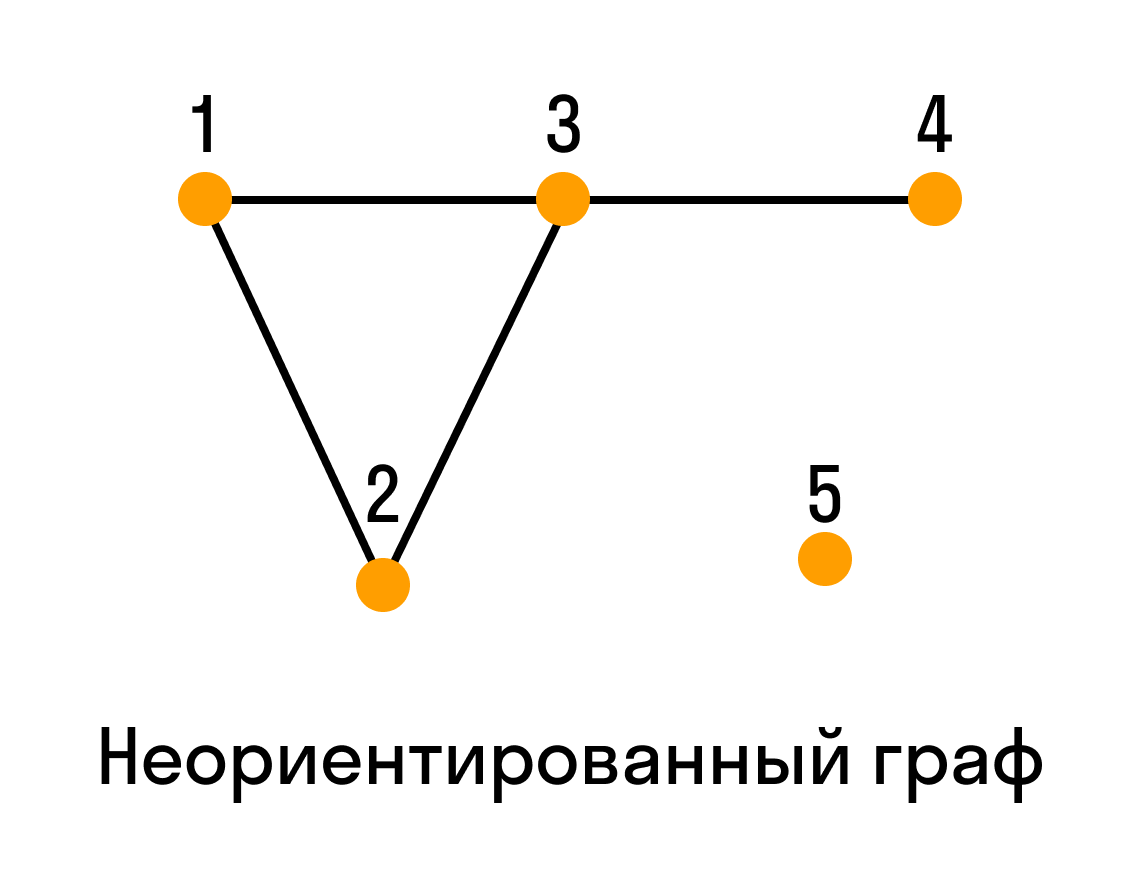
Ориентированные и неориентированные графы
Графы, в которых все ребра являются звеньями, то есть порядок двух концов ребра графа не существенен, называются неориентированными.
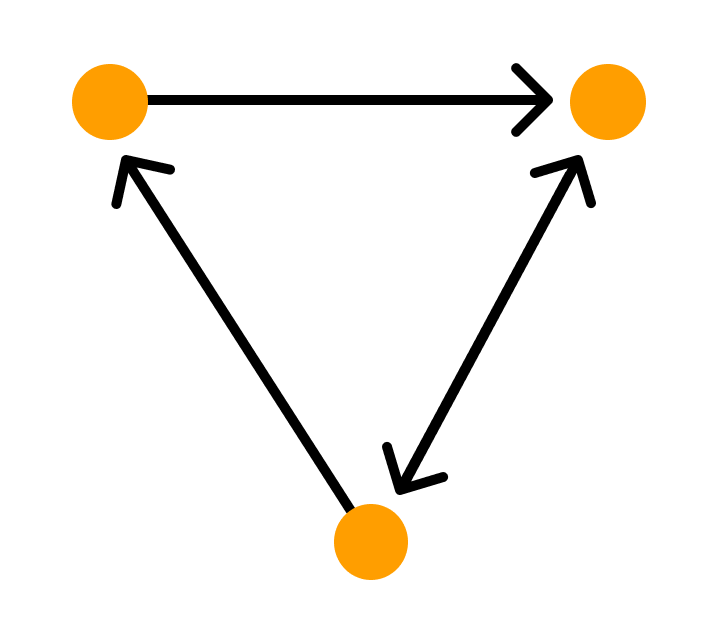
Графы, в которых все ребра являются дугами, то есть порядок двух концов ребра графа существенен, называются ориентированными графами или орграфами.
Неориентированный граф можно представить в виде ориентированного графа, если каждое его звено заменить на две дуги с противоположным направлением.
Графы с петлями, смешанные графы, пустые графы, мультиграфы, обыкновенные графы, полные графы
Если граф содержит петли — это обстоятельство важно озвучивать и добавлять к основной характеристике графа уточнение «с петлями». Если граф не содержит петель, то добавляют «без петель».
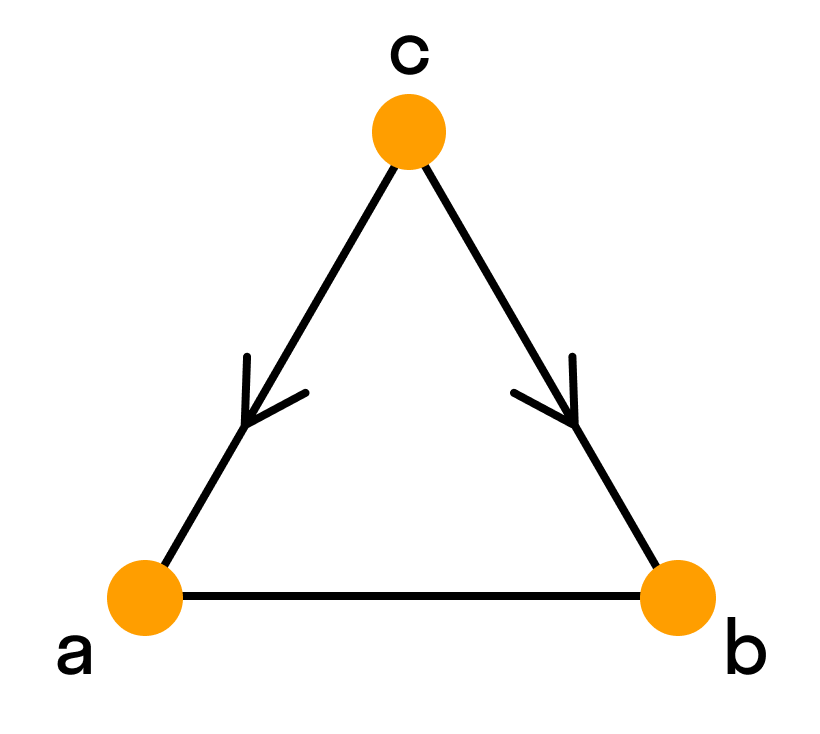
Смешанным называют граф, в котором есть ребра хотя бы двух из упомянутых трех разновидностей (звенья, дуги, петли).
Пустой граф — это тот, что состоит только из голых вершин.
Мультиграфом — такой граф, в котором пары вершин соединены более, чем одним ребром. То есть есть кратные рёбра, но нет петель.
Граф без дуг, то есть неориентированный, без петель и кратных ребер называется обыкновенным.
Граф называют полным, если он содержит все возможные для этого типа рёбра при неизменном множестве вершин. Так, в полном обыкновенном графе каждая пара различных вершин соединена ровно одним звеном.
Двудольный граф
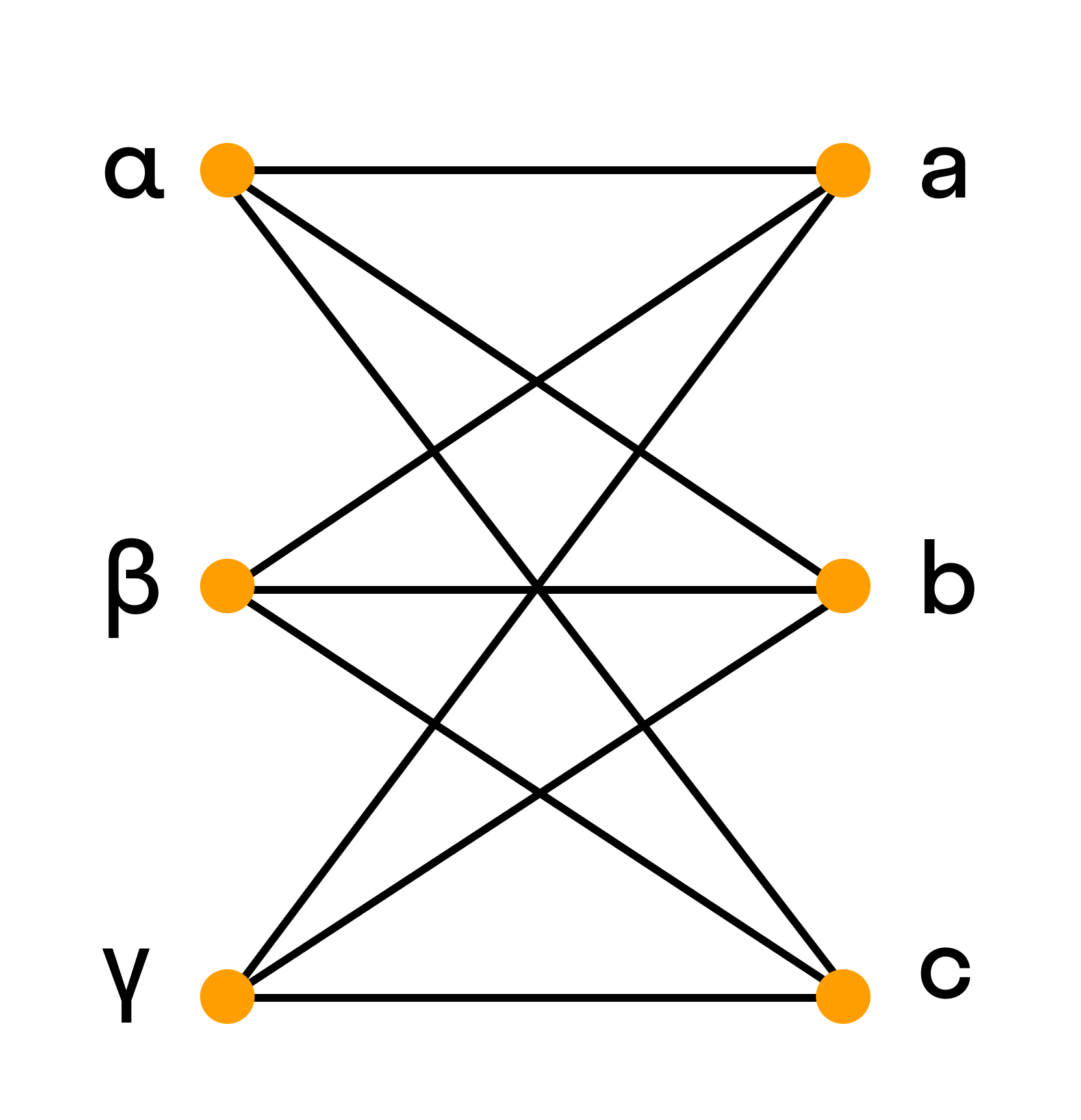
Граф называется двудольным, если множество его вершин можно разбить на два подмножества так, чтобы никакое ребро не соединяло вершины одного и того же подмножества.
Например, полный двудольный граф состоит из двух множеств вершин и из всевозможных звеньев, которые соединяют вершины одного множества с вершинами другого множества.
Эйлеров граф
Эйлеров граф отличен тем, что в нем можно обойти все вершины и при этом пройти одно ребро только один раз. В нём каждая вершина должна иметь только чётное число рёбер.
Пример. Является ли полный граф с одинаковым числом n рёбер, которым инцидентна каждая вершина, эйлеровым графом?
Регулярный граф
Регулярным графом называется связный граф, все вершины которого имеют одинаковую степень k.
Число вершин регулярного графа k-й степени не может быть меньше k + 1. У регулярного графа нечётной степени может быть лишь чётное число вершин.
Пример. Построить регулярный граф, в котором самый короткий цикл имеет длину 4.
Чтобы длина цикла соответствовала заданному условию, нужно чтобы число вершин графа было кратно четырем. Если число вершин равно четырём — получится регулярный граф, в котором самый короткий цикл имеет длину 3.
Увеличим число вершин до восьми (следующее кратное четырем число). Соединим вершины ребрами так, чтобы степени вершин были равны трём. Получаем следующий граф, удовлетворяющий условиям задачи:
Гамильтонов граф
Гамильтоновым графом называется граф, содержащий гамильтонов цикл.
Гамильтоновым циклом называется простой цикл, который проходит через все вершины рассматриваемого графа.
Говоря проще, гамильтонов граф — это такой граф, в котором можно обойти все вершины, и каждая вершина при обходе повторяется лишь один раз.
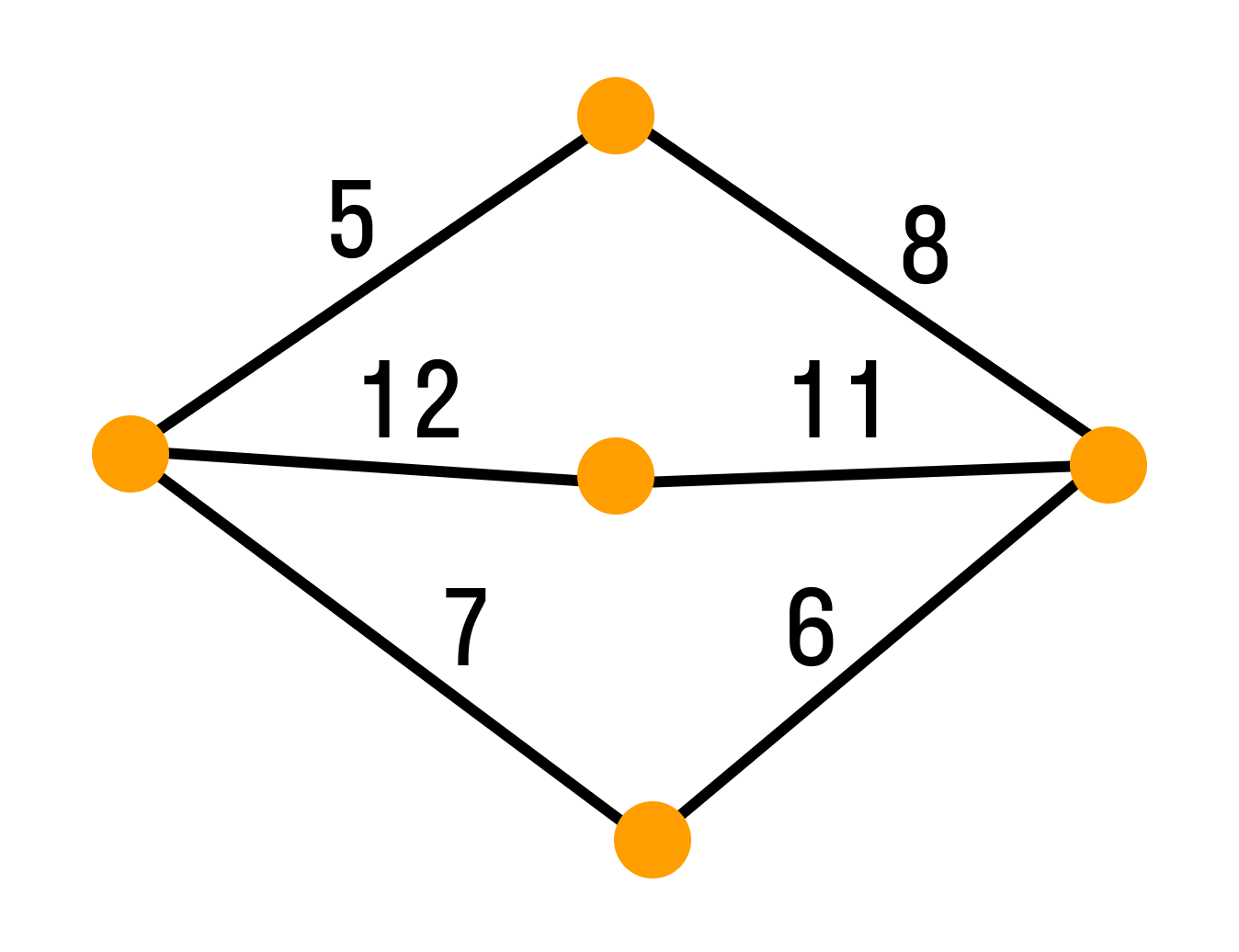
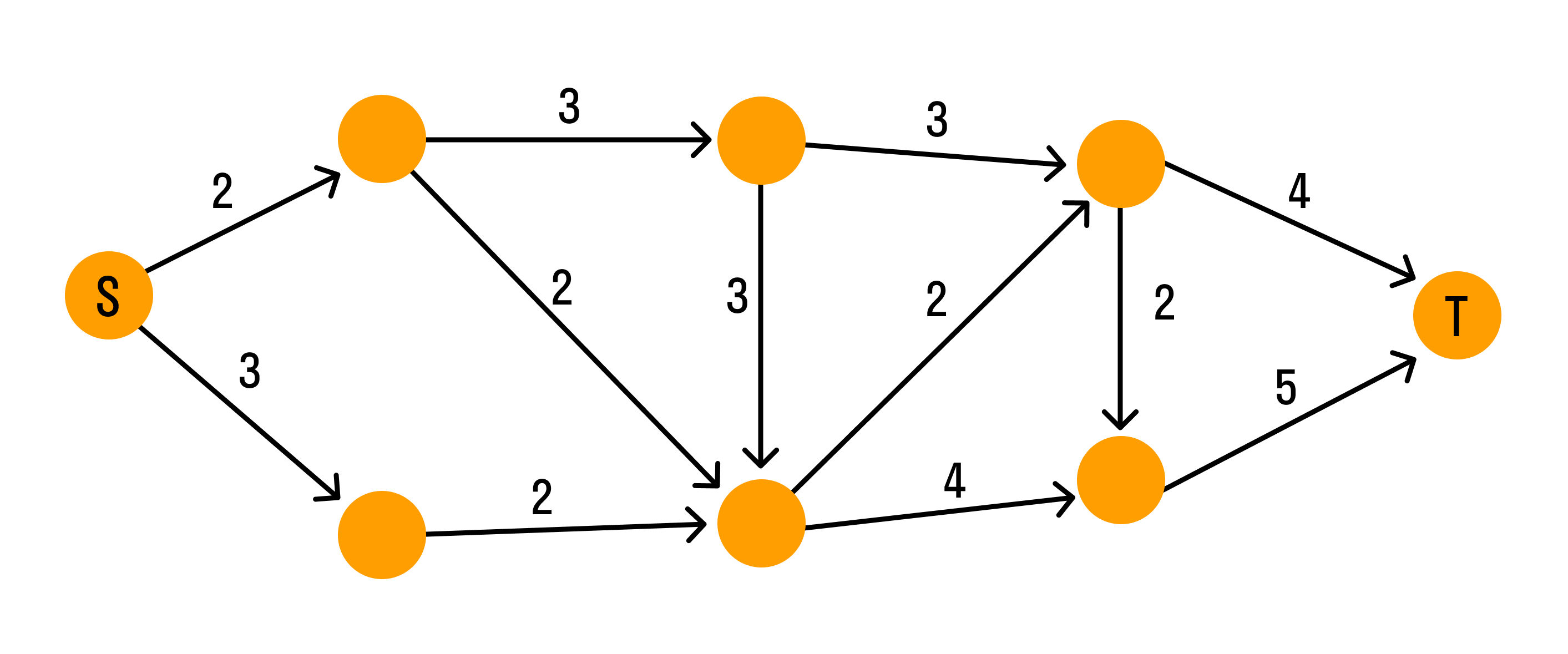
Взвешенный граф
Взвешенным графом называется граф, вершинам и/или ребрам которого присвоены «весы» — обычно некоторые числа. Пример взвешенного графа — транспортная сеть, в которой ребрам присвоены весы: они показывают стоимость перевозки груза по ребру и пропускные способности дуг.
Графы-деревья
Деревом называется связный граф без циклов. Любые две вершины дерева соединены лишь одним маршрутом.
Приведенное соотношение выражает критическое значение числа рёбер дерева, так как, если мы присоединим к дереву ещё одно ребро — будет создан цикл. А если уберем одно ребро, то граф-дерево разделится на две компоненты. Граф, состоящий из компонент дерева, называется лесом.
Определение дерева
Деревом называется связный граф, который не содержит циклов.
Таким образом, в дереве невозможно вернуться в исходную вершину, перемещаясь по ребрам и не проходя по одному ребру два или более раз.
Циклом называется замкнутый путь, который не проходит дважды через одну и ту же вершину.
Простым путем называется путь, в котором никакое ребро не встречается дважды.
Легко проверить, что дерево — это граф, в котором любые две вершины соединены ровно одним простым путем. Если выкинуть любое ребро из дерева, то граф станет несвязным. Поэтому:
Дерево — минимальный по числу рёбер связный граф.
Висячей вершиной называется вершина, из которой выходит ровно одно ребро.
Определения дерева:
Очень часто в дереве выделяется одна вершина, которая называется корнем дерева. Дерево с выделенным корнем называют корневым или подвешенным деревом. Пример: генеалогическое дерево.
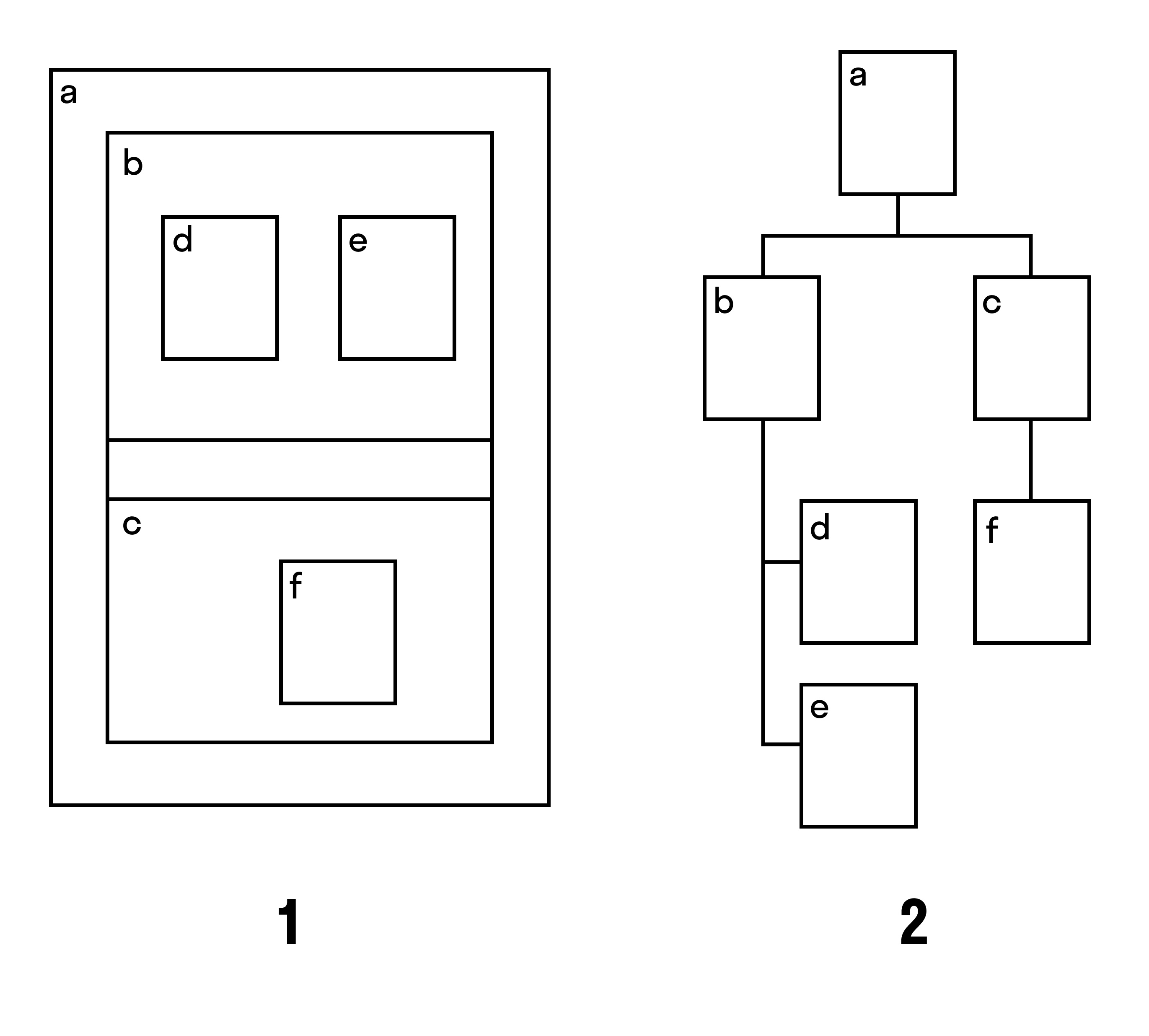
Когда изображают деревья, то часто применяют дополнительные соглашения, эстетические критерии и ограничения.
Например, при соглашении включения (рис. 1) вершины корневого дерева изображают прямоугольниками, а соглашение — опрокидывания (рис. 2) подобно классическому соглашению нисходящего плоского изображения корневого дерева. Вот так могут выглядеть разные изображения одного дерева:
Теоремы дерева и их доказательства
В дереве с более чем одной вершиной есть висячая вершина.
Доказательство первой теоремы:
Пойдем из какой-нибудь вершины по ребрам. Так как в дереве нет циклов, то мы не вернемся в вершину, в которой уже побывали. Если у каждой вершины степень больше 1, то найдется ребро, по которому можно уйти из неё после того, как мы пришли в нее.
Но поскольку количество вершин в дереве конечно, когда-нибудь мы остановимся в некоторой вершине. Противоречие. Значит, когда-нибудь мы дойдём в висячую вершину. Если же начать идти из неё, то мы найдём вторую висячую вершину.
В дереве число вершин на 1 больше числа ребер.
Доказательство второй теоремы:
Докажем по индукции по количеству вершин в дереве n. Если в дерево одна вершина, то факт верен. Предположим, что для всех n