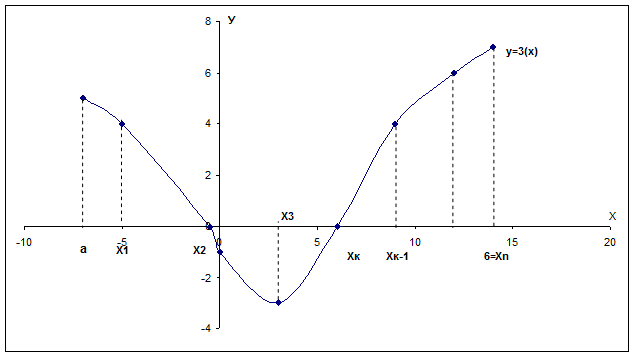
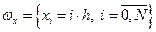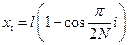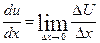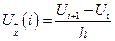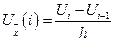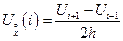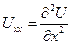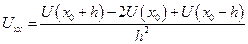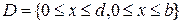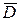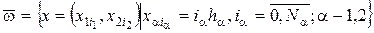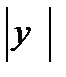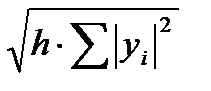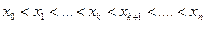Что такое сеточная функция
Сетки и сеточные функции



Метод конечных разностей.
Метод конечных разностей или меток сеток на сегодняшний день является одним из самых распространенных методов приближенного решения краевых задач. Суть метода в следующем:
1. Область непрерывного изменения аргумента заменяется областью дискретного аргумента, выделяются точки, называемые узлами. Наносится сетка.
2. Область непрерывного изменения функции заменяется областью дискретного изменения функции, когда функция определена только в узлах сетки и называется сеточной функцией.
3. Все производные, входящие в определяющие уравнение и краевые условия заменяются (аппроксимируются) алгебраическими соотношениями сеточных функций.
4. Вместо интегрирования дифференциального уравнения записывают разностную схему и решают систему линейных алгебраических уравнений.
При использовании МКР нужно:
2. Выбрать разностную схему;
3. Определить точность аппроксимации;
4. Проанализировать устойчивость и сходимость разностной схемы к точному решению;
5. Провести тестовый расчет.
Свойства разностного решения и, в частности, его близость к точному решению зависит от точного выбора сетки.
Рассмотрим несколько видов сеток.
1. Равномерная сетка
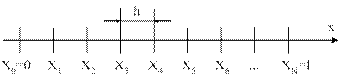 |
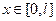
Разобьем этот отрезок точками 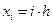
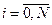
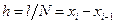
2. Неравномерная сетка получается в том случае, когда 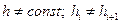
пример:
3. Сетка на плоскости.
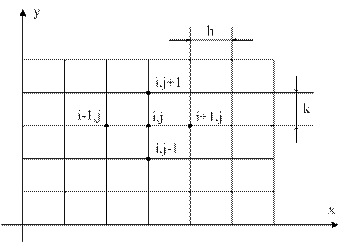 | Если шаги сетки по каждому из переменных (x, y) одинаковы, то сетка называется равномерной. Если же хотя бы по одной переменной шаг непостоянен, то сетка – неравномерная. Введение сетки: 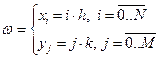 |
Метод конечных разностей сводится к замене производных, входящих в уравнения и краевые условия, разностными отношениями.
Классическое определение производной функции одной переменной записывается в виде:
Разложим функцию U в ряд Тейлора в окрестностях точки x0
 | 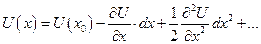 Положим, что Положим, что 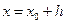 , получим: , получим: 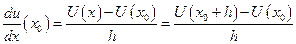 *11 Это равенство называется правой разностью. *11 Это равенство называется правой разностью. |
Другая форма записи правой разности:
Если 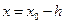
Существует также третья форма записи разностного отношения, называемая центральной разностью:
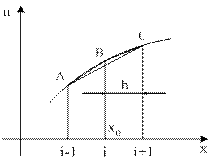
Если задана функция u(x), то графически интерпретация производных трёх типов содержат:
AB – левая разность;
CB – правая разность;
АС – центральная разность.
Узлы, которые задействованы в аппроксимации производной, называются шаблонами аппроксимации.
Получим разностное соотношение для второй производной:
Сначала представим Uxx через Ux, используя правую разность:
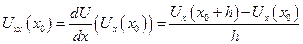
Далее производные 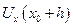
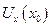
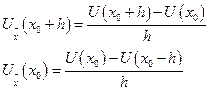
Подставив (5.2) в (5.1), получим:
С использованием сетки вторая производная имеет вид:
Сетки и сеточные функции
Метод конечных разностей (МКР)
Основные понятия
МКР, или метод сеток, в настоящее время является одним из наиболее распространенных методов приближенного решения краевых задач.
Суть метода в следующем:
1. Область непрерывного изменения аргумента (отрезок, прямоугольник и т.д.) заменяется конечным (дискретным) множеством точек (узлов), называемым сеткой.
2. Вместо функции непрерывного изменения аргумента рассматриваются функции дискретного аргумента, определенные в узлах сетки и называемые сеточными функциями.
3. Производные, входящие в дифференциальные уравнения и краевые условия, заменяются (аппроксимируются) разностными соотношениями, т.е. линейными комбинациями значений сеточных функций в некоторых узлах сетки.
4. В результате краевая задача для дифференциального уравнения заменяется системой линейных, если исходная задача была линейной, алгебраических уравнений – разностной схемой.
Если, полученная таким образом задача разрешима и ее решение при измельчении сетки приближается (сходится) к решению исходной задачи для дифференциального уравнения, то оно и принимается за приближенное решение исходной задачи.
Несмотря на внешнюю простоту метода, прежде, чем приступить к решению конкретной задачи, необходимо уметь дать ответы на следующие вопросы:
1) как выбрать сетку?
2) Как написать разностную схему?
3) Насколько хорошо разностная схема аппроксимирует исходную задачу?
4) Устойчива ли разностная схема и в каком смысле?
5) Какова скорость сходимости решения разностной задачи к решению исходной задачи?
Сетки и сеточные функции
Свойства разностного решения и, в частности, его близость к точному решению зависит от выбора сетки. Расположение узлов сетки в области может быть произвольным и определяться спецификой решаемой задачи. Рассмотрим несколько примеров
1) равномерная сетка на отрезке
2) неравномерная сетка на отрезке
Очевидно, что 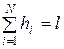
3) равномерная сетка на плоскости
Рассмотрим множество функций 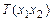
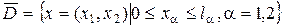
например,
Построим на каждом отрезке 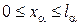
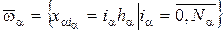
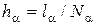
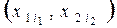
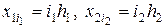
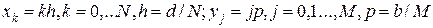
Эта сетка равномерна по каждому из переменных 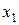
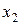

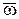
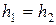
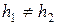
4) сетка на плоскости в произвольной области
Пусть на плоскости 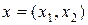
Тогда на плоскости получим сетку с узлами 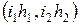

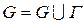
Узлы, попавшие внутрь G, назовем внутренними узлами и обозначим их совокупность 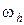

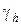
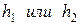
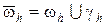
Построение разностной схемы проводится таким образом, чтобы получаемая в результате решения сеточная функция была как можно ближе к искомой непрерывной функции.
Вместо функций 
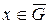
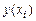
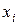
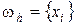
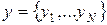
Для оценки близости приближенного решения (решения на сетке) к точному решению исходной краевой задачи можно использовать два способа
1. Производится интерполяция сеточной функции на все точки области G, после чего определяется норма разности 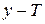
2. Точное решение 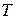
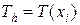
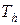
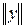
а) сеточный аналог чебышевской нормы в пространстве непрерывных функций С
б) сеточный аналог гильбертовой нормы в 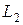

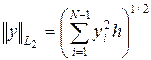
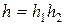
Тогда если при бесконечном дроблении сетки величина 
Сеточная функция. Пространство сеточных функций. Нормы сеточных функций
Функция y=y(xi) дискретного аргумента xi называется сеточной функцией, определенной на сетке 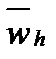
Сеточная область wh зависит от параметра h. При различных значениях параметра h имеем различные сеточные области. Поэтому и сеточные функции yh(x) зависят от параметра h.
Функции u(x) непрерывного аргумента являются элементами функционального пространства H. Множество сеточных функций yh(x) образует пространство Hh. Таким образом, в методе сеток пространство H заменяется на Hh сеточных функций yh(x).
Так как рассматривается множество сеток
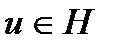



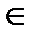
Соответствие функций u(x) и uh можно установить различными способами, например,
uh=u(x), x 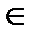
В линейном пространстве Hh введем норму ||.||Hh, которая является аналогом нормы ||.||Н в исходном пространстве Н. Обычно принято выбирать норму в пространстве Hh так, чтобы при стремлении к нулю h она переходила в ту или иную норму функций, заданных на всем отрезке, т.е. чтобы выполнялось условие: 

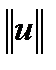
Условие (2) называют условием согласования в пространствах Hh и Н.
Рассмотрим простейшие типы норм в Hh для случая сеток wh=
1. Норма 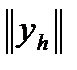
удовлетворяет условию (2), если в качестве Н рассматривать пространство непрерывных функций с нормой 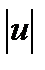
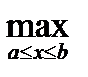

а сеточную функцию определять как yh(x)=uh(x), x 
2. Норма 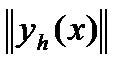
а сеточную функцию определять в виде yh=uh(x), x 
Сеточные функции
Дата добавления: 2015-01-16 ; просмотров: 1018 ; Нарушение авторских прав
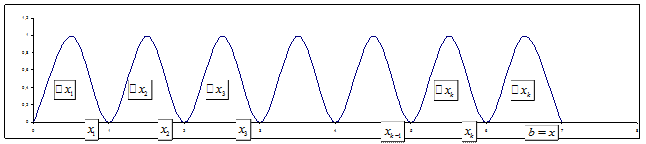
Пусть функция 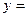

Разобьём 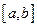
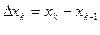
Если шаг сетки 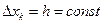
Если область определении функции
D(ƒ)= 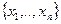
(в общем случае, множество 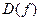
Для удобства выполнения взаимно однозначна отображение.
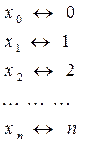
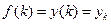
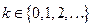
В экономике сеточная функция встречается:
1. Рост процентного вклада
2. Величина долга по займу с регулярными выплатами
4. Модель делового цикла (Самуэльсона-Хикса)