Что такое симметрическая разность множеств
Симметрическая разность
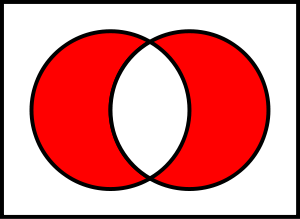
Симметрическая разность двух множеств — это теоретико-множественная операция, результатом которой является множество элементов этих множеств, принадлежащих только одному из них. Симметрическая разность множеств 


Содержание
Определение
Симметрическую разность можно ввести двумя способами:
Понятие симметрической разности можно обобщить на число множеств, большее двух.
Свойства
Пример
См. также
Литература
Полезное
Смотреть что такое «Симметрическая разность» в других словарях:
СИММЕТРИЧЕСКАЯ РАЗНОСТЬ — множеств одна из операций над множествами. Пусть имеются два множества Аи В. Тогда их симметрическая разность обозначается ADB и определяется равенствами где символы означают соответственно операции объединения, пересечения, разности и дополнения … Математическая энциклопедия
СИММЕТРИЧЕСКАЯ РАЗНОСТЬ — порядка пв точке хфункции действительного переменного f(x) выражение Часто также симметрич. разностью называют выражение получающееся из вышеприведенного заменой hна 2h. Если функция f(x).имеет в точке хпроизводную fn (х).порядка п, то Т. П.… … Математическая энциклопедия
Разность множеств — Не следует путать с Симметрическая разность. Разность двух множеств это теоретико множественная операция, результатом которой является множество, в которое входят все элементы первого множества, не входящие во второе множество. Обычно… … Википедия
АЛГЕБРА ЛОГИКИ — система алгебраич. методов решения логич. задач, а также совокупность задач, решаемых такими методами. А. л. в узком смысле слова алгебраич. (табличное, матричное) построение классич. логики высказываний, в котором рассматриваются… … Философская энциклопедия
Симметричность — может означать: Симметрия Симметричная операция (от нескольких операндов) Симметричная функция (от нескольких переменных) Симметрический многочлен в математической логике: Симметричное отношение в линейной алгебре: Симметричный тензор… … Википедия
Теория множеств — Теория множеств раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой… … Википедия
Операции над множествами — Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико множественными операциями или сет операциями. В результате операций из исходных множеств получаются новые … Википедия
Операция над множествами — Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико множественными операциями или сет операциями. В результате операций из исходных множеств получаются новые … Википедия
ИСЧИСЛЕНИЕ КЛАССОВ — аксиоматич. (см. Аксиоматический метод) описание логики классов. И. к. рав нообъёмно исчислению одноместных предикатов (см. Логика предикатов): у этих исчислений совпадают классы как исходных формул, так и выводимых формул (теорем);… … Философская энциклопедия
Бинарные операции над упорядоченными множествами
В предыдущей статье я писал о бинарных операциях над неупорядоченными множествами. В этой статье мы рассмотрим алгоритмы с меньшей сложностью выполнения, для упорядоченных множеств.
I. Пересечение упорядоченных множеств
Пересечение двух упорядоченных множеств A и B — это множество только с теми элементами A и B, которые одновременно принадлежат обоим множествам, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных множеств A и B соответственно.
Сделал небольшую анимацию, чтобы показать как работает алгоритм.
Пример реализации на javascript:
Обращение к функции:
II. Разность упорядоченных множеств
Разность двух упорядоченных множеств A и B — это множество с элементами A, не совпадающими с элементами B, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных упорядоченных множеств A и B соответственно.
III. Объединение упорядоченных множеств
Объединение двух упорядоченных множеств A и B — это множество с элементами A и элементы множества B, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных упорядоченных множеств A и B соответственно.
IV. Симметрическая разность упорядоченных множеств
Симметрическая разность двух упорядоченных множеств A и B — это такое множество, куда входят все те элементы первого упорядоченного множества, которые не входят во второе упорядоченное множество, а также те элементы второго упорядоченного множества, которые не входят в первое упорядоченное множество. Сложность алгоритма O(2(m+n)), где m и n — длины входных упорядоченных множеств A и B соответственно.
По сути это вычитание множеств, сначала A из B, затем B из A.
Что такое симметрическая разность множеств
Объединение множеств X и Y — это множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств X или Y, т.е. принадлежат X или принадлежат Y.
Объединение X и Y обозначается через X∪Y
Формально x∈X∪Y ⇔ x∈X или x∈Y
Пример 3. Если X — множество точек левого круга и Y — множество точек правого круга, то
X∪Y — заштрихованная область, ограниченная обоими кругами.
представляет собой множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств данной системы М.
Для объединенных множеств справедливы:
справедливость которых вытекает из того, что левая и правая части равенств состоят из одних и тех же элементов.
Очевидно, что X∪∅ = X. Отсюда можно видеть, что ∅ играет роль нуля в алгебре множеств.
2. Пересечение множеств
Пересечение множеств X и Y — это множество, состоящее из всех тех и только тех элементов, которые принадлежат как множеству X, так и множеству Y.
Пересечение множеств обозначается X∩Y.
Формально x∈X∩Y ⇔ x∈X и x∈Y
Пример 5. Если Х — множество точек левого круга, а Y — множество точек правого круга, то X∩Y представляет собой заштрихованную область, являющуюся общей частью обоих кругов.
Множества X и Y называются непересекающимися (дизъюнктными), если они не имеют общих элементов, то есть если X∩Y=∅.
Частный случай: кортеж длины 1 —
кортеж длины 0 — или ∧ — пустой кортеж.
Отличие кортежа и обыкновенного множества: в кортеже могут быть одинаковые элементы.
Упорядоченные множества, элементами которых являются вещественные числа, будем называть векторами или точками пространства (n-мерного).
Два вектора равны, если они имеют одинаковую длину и соответствующие координаты их равны.
Компонентами кортежа (вектора) могут быть также компоненты кортежи (векторы):
Пример. Слова в предложении,
Прямое произведение множеств
Прямым (декартовым) произведением множеств X и Y называется множество, состоящее из всех тех и только тех упорядоченных пар, первая компонента которых принадлежит множеству X, а вторая принадлежит множеству Y.
Пример 3. Пусть X и Y — отрезки вещественной оси. Прямое произведение X*Y изображается заштрихованным прямоугольником. См. рис. б).
Прямое произведение изменяется при изменении порядка сомножителей т.е.
Очевидно X*Y = ∅ ⇔ X = ∅ или Y = ∅.
Частным случаем прямого произведения является понятие степеней (декартовых) множества — прямое произведение одинаковых множеств
M s =M*M*. *M, M 1 =M, M 0 =∧.
Обычно R — множество вещественных чисел, тогда R 2 =R*R — вещественная плоскость и R 3 =R*R*R — трехмерное вещественное пространство.
Проекция множества.
Операция программирования множества тесно связана с операцией проектирования кортежа и может применяться лишь к таким множествам, элементами которых являются кортежи одинаковой длины.
Пусть M — множество, состоящее из кортежей длины S. Тогда пролинией множества M будем называть множество пролиний всех кортежей из М
Очевидно что если М=Х*Y то Пр1М=Х, Пр2М=Y
и если Q⊆Х*Y то Пр1Q⊆Х и Пр2Q⊆Y
Пусть V — множество векторов одинаковой длины S.
В общем случае ПрiV — вовсе не обязательно прямое произведение: оно может быть подмножеством.
> 
>
СОДЕРЖАНИЕ
Характеристики
А \ треугольник В \ треугольник С> 
> 
>
Симметричная разница также может быть выражена с помощью операции XOR ⊕ для предикатов, описывающих два набора в нотации создателя множеств :
Симметричная разница также может быть выражена как объединение двух множеств за вычетом их пересечения :
Из свойства инверсий в булевой группе следует, что симметричная разность двух повторяющихся симметричных разностей эквивалентна повторяющейся симметричной разности соединения двух мультимножеств, где для каждого двойного множества обе могут быть удалены. Особенно:
Пересечение распределяется по симметричной разнице:
К другим свойствам симметричной разницы относятся:
Эта операция имеет те же свойства, что и симметричная разность множеств.
Повторяющаяся симметричная разность в некотором смысле эквивалентна операции над мультимножеством множеств, дающей набор элементов, которые находятся в нечетном количестве множеств.
Как и выше, симметричная разность набора наборов содержит только элементы, которые находятся в нечетном количестве наборов в коллекции:
Симметричная разность на пространствах с мерой
Пока существует понятие «насколько велик» набор, симметричная разница между двумя наборами может считаться мерой того, насколько «далеко друг от друга» они находятся.
является псевдометрикой на Σ. d μ становится метрикой, если Σ рассматривается по модулю отношения эквивалентности X
Расстояние Хаусдорфа против симметричной разности
Расстояние Хаусдорфа и (площадь) симметричной разности являются псевдометриками на множестве измеримых геометрических фигур. Однако они ведут себя совершенно иначе. На рисунке справа показаны две последовательности фигур: «Красный» и «Красный ∪ Зеленый». Когда расстояние Хаусдорфа между ними становится меньше, площадь симметричной разницы между ними становится больше, и наоборот. Продолжая эти последовательности в обоих направлениях, можно получить две последовательности, в которых расстояние Хаусдорфа между ними сходится к 0, а симметричное расстояние между ними расходится, или наоборот.
Симметричная разница
> 

>
А \ треугольник В \ треугольник С> 

> 

>
Симметричная разница также может быть выражена с помощью операции XOR ⊕ для предикатов, описывающих два набора в нотации создателя множеств :
Симметричная разница также может быть выражена как объединение двух множеств за вычетом их пересечения :
Из свойства инверсий в булевой группе следует, что симметричная разность двух повторяющихся симметричных разностей эквивалентна повторяющейся симметричной разности соединения двух мультимножеств, где для каждого двойного множества обе могут быть удалены. В частности:
Пересечение распределяется по симметричной разнице:
К другим свойствам симметричной разницы относятся:
Эта операция имеет те же свойства, что и симметричная разность множеств.
Повторяющаяся симметричная разность в некотором смысле эквивалентна операции над мультимножеством наборов, дающей набор элементов, которые находятся в нечетном количестве наборов. [ требуется разъяснение ]
Как и выше, симметричная разность набора наборов содержит только элементы, которые находятся в нечетном количестве наборов в коллекции:
Пока существует понятие «насколько велик» набор, симметричная разница между двумя наборами может считаться мерой того, насколько «далеко друг от друга» они находятся.
является псевдометрикой на Σ. d μ становится метрикой, если Σ рассматривается по модулю отношения эквивалентности X
Расстояние Хаусдорфа и (площадь) симметричной разности являются псевдометриками на множестве измеримых геометрических фигур. Однако они ведут себя совершенно иначе. На рисунке справа показаны две последовательности фигур: «Красный» и «Красный ∪ Зеленый». Когда расстояние Хаусдорфа между ними становится меньше, площадь симметричной разницы между ними становится больше, и наоборот. Продолжая эти последовательности в обоих направлениях, можно получить две последовательности, в которых расстояние Хаусдорфа между ними сходится к 0, а симметричное расстояние между ними расходится, или наоборот.