Что такое симметричная разность множеств
Диаграммы Эйлера-Венна
Что такое диаграммы Эйлера-Венна
Диаграмма Эйлера-Венна — геометрическая схема, которая используется для моделирования множеств и для схематичного изображения и отношений между ними.Диаграмма позволяет наглядно отразить различные утверждения о множествах. При использовании этого метода универсальное множество изображается в виде прямоугольника, подмножества изображают кругами. Диаграммы нашли свое применение в математике, логике, менеджменте и других прикладных направлениях.
Для отражения отношений между множествами математики Джон Венн и Леонард Эйлер использовали для способа. Если Венн использовал для обозначения множеств замкнутые фигуры, то Эйлер использовал круги.
Диаграммы Эйлера-Венна являются важным частным случаем кругов Эйлера. Диаграммы изображают все 2^n комбинаций n свойств, что является конечной булевой алгеброй. В случае n = 3 диаграмма Эйлера-Венна обычно состоит из трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приближенно равным длине стороны треугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Принцип построения
Построение диаграммы Эйлера-Венна — это изображение большого прямоугольника, который представляет универсальное множество U. Внутри прямоугольника изображаются замкнутые фигуры, обозначающие множества. Если множеств не более 3, то изображаются круги, и эллипсы, если множеств 4. Фигуры пересекаются в наиболее общем случае, требуемом задачей, что обозначается соответствующим образом.
Предположим, что на диаграмме изображен круг, представляющий множество А. Область в середине круга множества А отражает истинность выражения А, в то время как область вне круга обозначает ложь. Логическая операция будет отображаться на диаграмме при помощи штриховки тех областей, в которых ее значения истинны. В соответствии с алгеброй логики, конъюнкция множеств А и B будет истинна только тогда, когда истинны оба множества. Тогда на диаграмме будет отмечена область пересечения множеств.
С помощью диаграмм Эйлера-Венна можно доказать все законы алгебры, представляя их графически. Это возможно через выполнение следующего алгоритма:
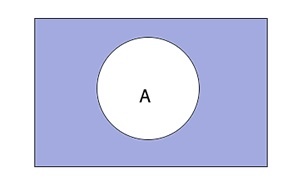
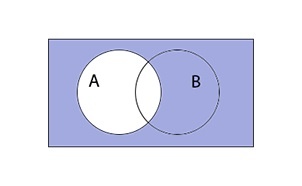
Дополнение множества
При этом не все элементы, не являющиеся элементами А, могут быть включены в \(\overline A.\) Принято считать, что все множества, которые участвуют в решении задачи, являются подмножествами некоторого общего универсального множества U. Учитывая это, дополнение \overline A определяется следующим образом:
Таким образом выглядит дополнение \(\overline A\) графически:
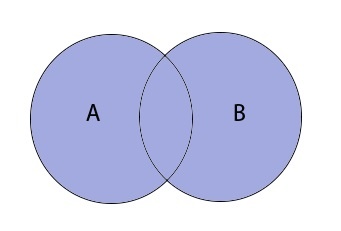
Объединение множеств
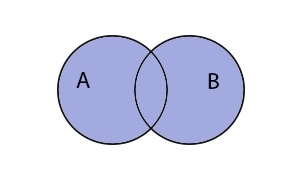
Объединение записывается следующим образом:
Таким образом объединение множеств выглядит графически:
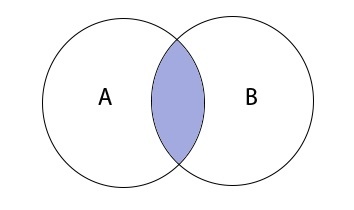
Пересечение множеств
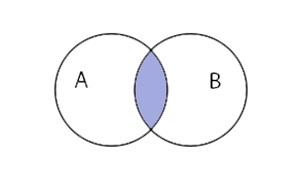
Пересечение множеств записывается следующим образом:
Таким образом пересечение множеств выглядит графически:
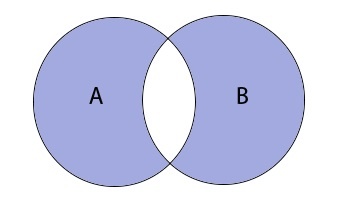
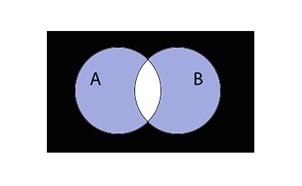
Симметричная разность множеств
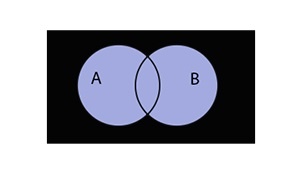
Симметричная разность A \ B — это такое множество, куда входят все те элементы первого множества, которые не входят во второе множество, а, также те элементы второго множества, которые не входят в первое множество
Разность множеств записывается следующим образом:
\(A\bigtriangleup B=(A\backslash B)\cup(B\backslash A)\)
Таким образом разность выглядит графически:
Разность множеств
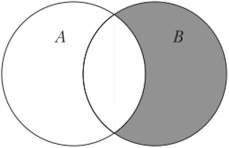
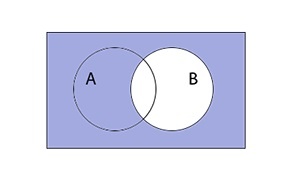
Разностью A \ B является множество элементов A, не входящих в B.
Разность множеств записывается следующим образом:
Таким образом разность выглядит графически:
Использование диаграмм Эйлера-Венна для доказательства логических равенств
Рассмотрим, как диаграммы Эйлера-Венна применяются для доказательства логических равенств.
Предположим, что перед нами конъюнкция множеств \(A\;\wedge\;B\)
В первую очередь обратим внимание на левую часть равенства. Построим диаграмму для множеств А и B. Графически отметим дизъюнкцию, заштриховав оба круга цветом.
Теперь отобразим инверсию, заштриховав область за пределами множеств.
Обратим внимание на правую часть равенства. В первую очередь отобразим инверсию A штриховкой область за пределами круга множества A цветом.
Проведем аналогичную операцию с множеством B.
Теперь штриховкой черным цветом всех областей пересечения отобразим конъюнкцию инверсий множеств А и B.
При сравнении области для отображения правой и левой частей, становится очевидно, что они равны. Справедливость логического равенства доказана с помощью диаграммы Эйлера-Венна.
Примеры задач с решением
Задача
Группа туристов из 100 человек пробыла в городе N три дня. За это время в ресторане питались 28 туристов, фастфуде — 42, кофейне — 30. И в ресторане, и в фастфуде побывало 10 человек; в ресторане и кофейне — 8; в фастфуде и кофейне — 5. Все во всех трех местах побывали три человека. Сколько туристов питалось в других местах и не посетило ни одного из перечисленных?
Решение
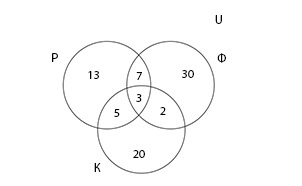
В условии задачи три множества — Р, Ф и К. Туристы, которые пытались в ресторане, фастфуде и кофейне, соответственно. Универсальное множество U — это множество всех туристов группы. Запишем условие задачи, где n(X) — количество элементов множества X.
Необходимо найти \(n(Р\;\cup\;Ф\;\cup\;К)\;=\;n\;(U\;\backslash\;(Р\;\cap\;Ф\;\cap\:К))\)
В решении задачи поможет представление данных графически с помощью диаграммы Эйлера-Венна. Составляя ее, важно помнить, что если в \(Р\;\cap\;Ф\;\cap\:К\) три элемента, а в множестве \(Р\;\cap\;Ф\) — 10 элементов, то в диаграмме в месте пересечений множеств Р и Ф мы проставляем 7 элементов, так как 3 элемента уже учтено.
Теперь, когда на диаграмме все элементы учтены по одному разу, можно вычислить количество туристов, которые побывали хотя бы одном из заведений.
Тогда, количество туристов, которые не побывали ни в ресторане, ни в фастфуде, ни в кофейне можно вычислить следующим образом:
Ответ: 20 туристов не побывали ни в одном из указанных заведений.
Задача
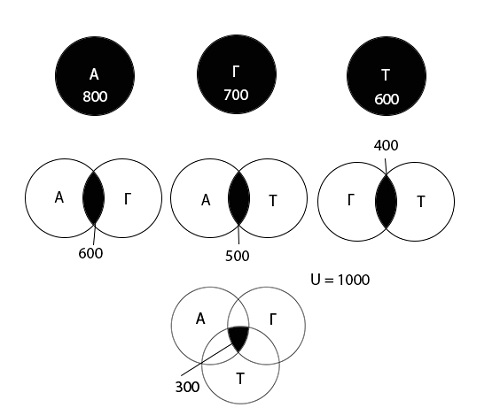
На олимпиаде по математике школьникам предложили решить три задачи: одну по алгебре, одну по геометрии, одну по тригонометрии. В олимпиаде участвовало 1000 школьников. Результаты олимпиады были следующие: задачу по алгебре решили 800 участников, по геометрии — 700, по тригонометрии — 600. 600 школьников решили задачи по алгебре и геометрии, 500 — по алгебре и тригонометрии, 400 — по геометрии и тригонометрии. 300 человек решили задачи по алгебре, геометрии и тригонометрии. Сколько школьников не решило ни одной задачи?
Решение
Начнем с определения множеств и введения обозначений. В данном случае, их три:
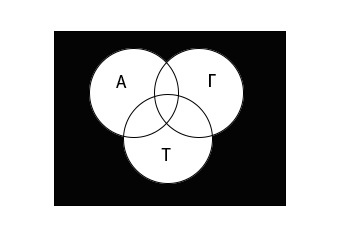
Используя диаграмму Эйлера-Венна графически изобразим информацию, данную в условии задачи.
Теперь используя диаграмму, обозначим область, которую необходимо найти:
Определим количество школьников для всех возможных областей.
Обозначим искомую область А = 0, Г = 0, Т = 0 как «х».
Найдем остальные области:
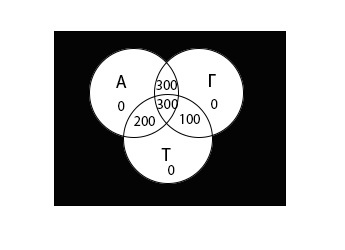
Теперь внесем значения всех областей в диаграмму:
\((A\;\cup\;Г\;\cup\;Т)\;=\; 0 + 0 + 0 + 300 + 300 + 200 + 100 = 900\)
Ответ: 100 школьников не решило ни одной задачи.
Бинарные операции над упорядоченными множествами
В предыдущей статье я писал о бинарных операциях над неупорядоченными множествами. В этой статье мы рассмотрим алгоритмы с меньшей сложностью выполнения, для упорядоченных множеств.
I. Пересечение упорядоченных множеств
Пересечение двух упорядоченных множеств A и B — это множество только с теми элементами A и B, которые одновременно принадлежат обоим множествам, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных множеств A и B соответственно.
Сделал небольшую анимацию, чтобы показать как работает алгоритм.
Пример реализации на javascript:
Обращение к функции:
II. Разность упорядоченных множеств
Разность двух упорядоченных множеств A и B — это множество с элементами A, не совпадающими с элементами B, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных упорядоченных множеств A и B соответственно.
III. Объединение упорядоченных множеств
Объединение двух упорядоченных множеств A и B — это множество с элементами A и элементы множества B, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных упорядоченных множеств A и B соответственно.
IV. Симметрическая разность упорядоченных множеств
Симметрическая разность двух упорядоченных множеств A и B — это такое множество, куда входят все те элементы первого упорядоченного множества, которые не входят во второе упорядоченное множество, а также те элементы второго упорядоченного множества, которые не входят в первое упорядоченное множество. Сложность алгоритма O(2(m+n)), где m и n — длины входных упорядоченных множеств A и B соответственно.
По сути это вычитание множеств, сначала A из B, затем B из A.
Симметрическая разность
Симметрическая разность двух множеств — это теоретико-множественная операция, результатом которой является множество элементов этих множеств, принадлежащих только одному из них. Симметрическая разность множеств 


Содержание
Определение
Симметрическую разность можно ввести двумя способами:
Понятие симметрической разности можно обобщить на число множеств, большее двух.
Свойства
Пример
См. также
Литература
Полезное
Смотреть что такое «Симметрическая разность» в других словарях:
СИММЕТРИЧЕСКАЯ РАЗНОСТЬ — множеств одна из операций над множествами. Пусть имеются два множества Аи В. Тогда их симметрическая разность обозначается ADB и определяется равенствами где символы означают соответственно операции объединения, пересечения, разности и дополнения … Математическая энциклопедия
СИММЕТРИЧЕСКАЯ РАЗНОСТЬ — порядка пв точке хфункции действительного переменного f(x) выражение Часто также симметрич. разностью называют выражение получающееся из вышеприведенного заменой hна 2h. Если функция f(x).имеет в точке хпроизводную fn (х).порядка п, то Т. П.… … Математическая энциклопедия
Разность множеств — Не следует путать с Симметрическая разность. Разность двух множеств это теоретико множественная операция, результатом которой является множество, в которое входят все элементы первого множества, не входящие во второе множество. Обычно… … Википедия
АЛГЕБРА ЛОГИКИ — система алгебраич. методов решения логич. задач, а также совокупность задач, решаемых такими методами. А. л. в узком смысле слова алгебраич. (табличное, матричное) построение классич. логики высказываний, в котором рассматриваются… … Философская энциклопедия
Симметричность — может означать: Симметрия Симметричная операция (от нескольких операндов) Симметричная функция (от нескольких переменных) Симметрический многочлен в математической логике: Симметричное отношение в линейной алгебре: Симметричный тензор… … Википедия
Теория множеств — Теория множеств раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой… … Википедия
Операции над множествами — Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико множественными операциями или сет операциями. В результате операций из исходных множеств получаются новые … Википедия
Операция над множествами — Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико множественными операциями или сет операциями. В результате операций из исходных множеств получаются новые … Википедия
ИСЧИСЛЕНИЕ КЛАССОВ — аксиоматич. (см. Аксиоматический метод) описание логики классов. И. к. рав нообъёмно исчислению одноместных предикатов (см. Логика предикатов): у этих исчислений совпадают классы как исходных формул, так и выводимых формул (теорем);… … Философская энциклопедия
> 
>
СОДЕРЖАНИЕ
Характеристики
А \ треугольник В \ треугольник С> 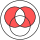
> 
>
Симметричная разница также может быть выражена с помощью операции XOR ⊕ для предикатов, описывающих два набора в нотации создателя множеств :
Симметричная разница также может быть выражена как объединение двух множеств за вычетом их пересечения :
Из свойства инверсий в булевой группе следует, что симметричная разность двух повторяющихся симметричных разностей эквивалентна повторяющейся симметричной разности соединения двух мультимножеств, где для каждого двойного множества обе могут быть удалены. Особенно:
Пересечение распределяется по симметричной разнице:
К другим свойствам симметричной разницы относятся:
Эта операция имеет те же свойства, что и симметричная разность множеств.
Повторяющаяся симметричная разность в некотором смысле эквивалентна операции над мультимножеством множеств, дающей набор элементов, которые находятся в нечетном количестве множеств.
Как и выше, симметричная разность набора наборов содержит только элементы, которые находятся в нечетном количестве наборов в коллекции:
Симметричная разность на пространствах с мерой
Пока существует понятие «насколько велик» набор, симметричная разница между двумя наборами может считаться мерой того, насколько «далеко друг от друга» они находятся.
является псевдометрикой на Σ. d μ становится метрикой, если Σ рассматривается по модулю отношения эквивалентности X
Расстояние Хаусдорфа против симметричной разности
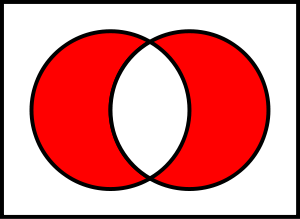
Расстояние Хаусдорфа и (площадь) симметричной разности являются псевдометриками на множестве измеримых геометрических фигур. Однако они ведут себя совершенно иначе. На рисунке справа показаны две последовательности фигур: «Красный» и «Красный ∪ Зеленый». Когда расстояние Хаусдорфа между ними становится меньше, площадь симметричной разницы между ними становится больше, и наоборот. Продолжая эти последовательности в обоих направлениях, можно получить две последовательности, в которых расстояние Хаусдорфа между ними сходится к 0, а симметричное расстояние между ними расходится, или наоборот.
Симметричная разница
> 
>
Содержание
Свойства [ править ]
А \ треугольник В \ треугольник С> 
> 
>
Симметричная разница также может быть выражена с помощью операции XOR ⊕ над предикатами, описывающими два набора в нотации построителя множеств :
Симметричная разница также может быть выражена как объединение двух множеств за вычетом их пересечения :
Симметричная разность коммутативна и ассоциативна :
Из свойства инверсий в булевой группе следует, что симметричная разность двух повторяющихся симметричных разностей эквивалентна повторяющейся симметричной разности соединения двух мультимножеств, где для каждого двойного множества обе могут быть удалены. Особенно:
Пересечение распределяется по симметричной разнице:
К другим свойствам симметричной разницы относятся:
Эта операция имеет те же свойства, что и симметричная разность множеств.
Повторяющаяся симметричная разность в некотором смысле эквивалентна операции над мультимножеством наборов, дающей набор элементов, которые находятся в нечетном количестве наборов. [ требуется разъяснение ]
Как и выше, симметричная разность набора наборов содержит только элементы, которые находятся в нечетном количестве наборов в коллекции:
| △ M | = ∑ l = 1 n ( − 2 ) l − 1 ∑ 1 ≤ i 1 i 2 … i l ≤ n | M i 1 ∩ M i 2 ∩ … ∩ M i l | <\displaystyle |\triangle M|=\sum _
Симметричная разница в пространствах мер [ править ]
Пока существует понятие «насколько велик» набор, симметричная разница между двумя наборами может считаться мерой того, насколько «далеко друг от друга» они находятся.
является псевдометрикой на Σ. d μ становится метрикой, если Σ рассматривается по модулю отношения эквивалентности X
| μ ( X ) − μ ( Y ) | = | ( μ ( X ∖ Y ) + μ ( X ∩ Y ) ) − ( μ ( X ∩ Y ) + μ ( Y ∖ X ) ) | = | μ ( X ∖ Y ) − μ ( Y ∖ X ) | ≤ | μ ( X ∖ Y ) | + | μ ( Y ∖ X ) | = μ ( X ∖ Y ) + μ ( Y ∖ X ) = μ ( ( X ∖ Y ) ∪ ( Y ∖ X ) ) = μ ( X △ Y ) <\displaystyle <\begin
Расстояние Хаусдорфа против симметричной разности [ править ]
Расстояние Хаусдорфа и (площадь) симметричной разности являются псевдометриками на множестве измеримых геометрических фигур. Однако они ведут себя совершенно иначе. На рисунке справа показаны две последовательности фигур: «Красный» и «Красный ∪ Зеленый». Когда хаусдорфово расстояние между ними становится меньше, площадь симметричной разницы между ними становится больше, и наоборот. Продолжая эти последовательности в обоих направлениях, можно получить две последовательности, в которых расстояние Хаусдорфа между ними сходится к 0, а симметричное расстояние между ними расходится, или наоборот.