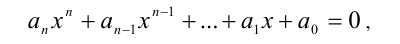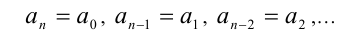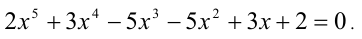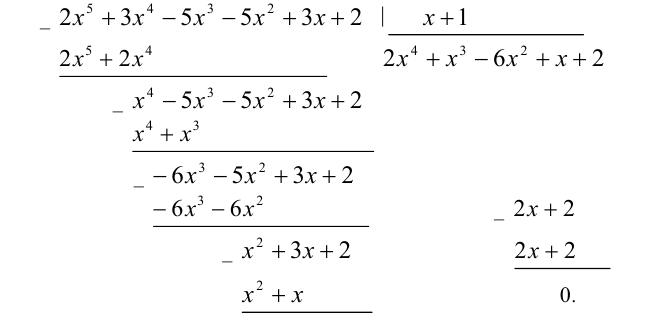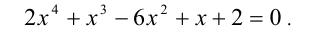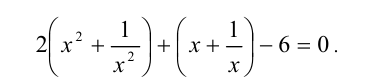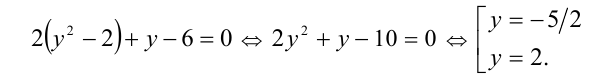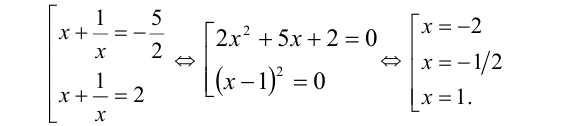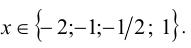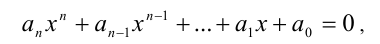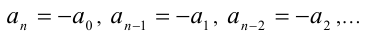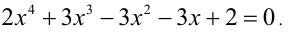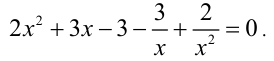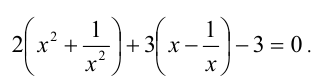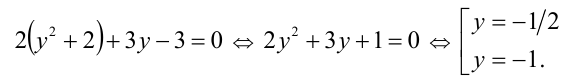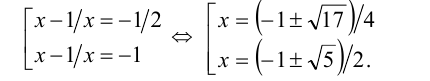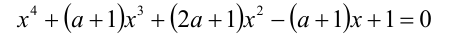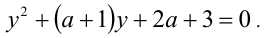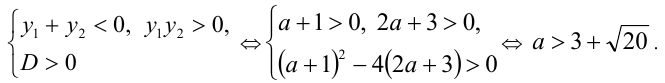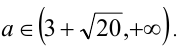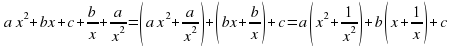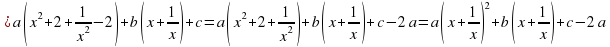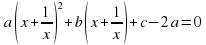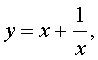Что такое симметричные уравнения
Симметрические и кососимметрические уравнения
Симметрические и кососимметрические уравнения
где равноотстоящие от концов многочлена коэффициенты равны, т.е.
Рассмотрим отдельно решение симметрических уравнений чётной и нечётной степеней [30].
Если 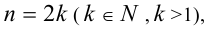
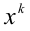
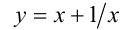
Если же 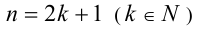
Пример №189.
Решить уравнение
Решение:
Очевидно, имеем симметрическое уравнение 5-й степени. Решаем его по изложенной выше схеме. Одним из корней уравнения будет число x = — 1. Найдём другие корни:
Решим симметрическое уравнение 4-й степени
Поделим для этого обе части уравнения на 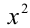
Обозначим у = x + (1/x), тогда
Выполняя обратную подстановку, получаем
Объединяя полученные решения, приходим к ответу:
где равноотстоящие от концов многочлена коэффициенты являются противоположными числами, т.е.
Решение кососимметрических уравнений чётной и нечётной степени во многом аналогично решению соответствующих симметрических уравнений.
Если 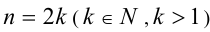
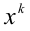
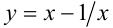
Пример №190.
Решить уравнение
Решение:
Это кососимметрическое уравнение 4-й степени. Поскольку x = 0 не является корнем уравнения, то поделим обе его части на 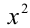
Перепишем последнее уравнение в виде
Положим у = х — (1/x), тогда получим
Выполняя обратную подстановку, получаем 4 решения
Пример №191.
Найти все значения параметра а , при которых уравнение
на промежутке 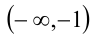
Решение:
Так как 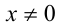
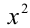
Поскольку функция у =x — (1/x) возрастает на промежутке 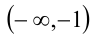
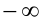
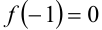
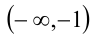
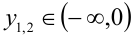
Ответ:
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Симметрические системы уравнений и системы, содержащие однородные уравнения
Разделы: Математика
Цели урока:
Тип урока: урок изучения нового материала.
Используемые технологии обучения:
Оборудование: компьютер, мультимедийный проектор.
За неделю до урока учащиеся получают темы творческих заданий (по вариантам).
I вариант. Симметрические системы уравнений. Способы решения.
II вариант. Системы, содержащие однородное уравнение. Способы решения.
Каждый ученик, используя дополнительную учебную литературу, должен найти соответствующий учебный материал, подобрать систему уравнений и решить её.
По одному учащемуся от каждого варианта создают мультимедийные презентации по теме творческого задания. Учитель при необходимости проводит консультации для учащихся.
Содержание урока
I. Мотивация учебной деятельности учащихся
Вступительное слово учителя
На предыдущем уроке мы рассматривали решение систем уравнений методом замены неизвестных. Общего правила выбора новых переменных не существует. Однако, можно выделить два вида систем уравнений, когда есть разумный выбор переменных:
II. Изучение нового материала
Учащиеся II варианта отчитываются о проделанной домашней работе.
1. Демонстрация слайдов мультимедийной презентации «Системы, содержащие однородное уравнение» (презентация 1).
Учащиеся записывают в тетради:
2. Работа в парах учащихся, сидящих за одной партой: учащийся II варианта объясняет соседу по парте решение системы, содержащей однородное уравнение.
Отчёт учащихся I варианта.
1. Демонстрация слайдов мультимедийной презентации «Симметрические системы уравнений» (презентация 2).
Учащиеся записывают в тетради:
2. Работа в парах учащихся, сидящих за одной партой: учащийся I варианта объясняет соседу по парте решение симметрической системы уравнений.
III. Закрепление изученного материала
Работа в группах (в группу по 4 ученика объединяются учащиеся, сидящие за соседними партами).
Каждая из 6 групп выполняет следующее задание.
Определить вид системы и решить её:
Учащиеся в группах анализируют системы, определяют их вид, затем, в ходе фронтальной работы обсуждают решения систем.
симметрическая, введем новые переменные x+y=u, xy=v
содержит однородное уравнение.
Пара чисел (0;0) не является решением системы.
IV. Контроль знаний учащихся
Самостоятельная работа по вариантам.
Решите систему уравнений:
Учащиеся сдают тетради учителю на проверку.
V. Домашнее задание
1. Выполняют все учащиеся.
Решите систему уравнений:
2.Выполняют «сильные» учащиеся.
Решите систему уравнений:
VI. Итог урока
Вопросы:
С какими видами систем уравнений вы познакомились на уроке?
Какой способ решения систем уравнений применяется при их решении?
Сообщение оценок, полученных учащимися в ходе урока.
Факультатив по математике «Симметрические и возвратные уравнения»
Описание разработки
Материал разделен на 3 части:
3) самостоятельная работа. Решение самостоятельной работы и её разбор помугут выяснить усвоена ли тема.
Симметрическим(симметричным) уравнением 3-ей степени называют уравнение вида
Решение уравнения осуществляется при помощи разложения левой части уравнения на множители
Симметрическими(симметричными) уравнениями 4-ой степени называют уравнения вида
Содержимое разработки
Факультатив по математике
Разработка занятия по теме:
Симметрические(симметричные) и возвратные уравнения.
Симметрическим(симметричным) уравнением 3-ей степени называют уравнение вида
ax 3 + bx 2 + bx + a = 0, где a, b – заданные числа.
Решение уравнения осуществляется при помощи разложения левой части уравнения на множители:
ax 3 + bx 2 + bx + a= (ax 3 + a) + (bx 2 + bx) = a(x 3 + 1) + bx(x + 1)= a(x + 1)(x 2 – x + 1) + bx(x + 1) = (x + 1)(ax 2 + ax + a + bx) = (x + 1)( ax 2 + (a + b)x + a) = 0 

Симметрическими(симметричными) уравнениями 4-ой степени называют уравнения вида
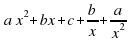
Преобразуем левую часть уравнения :
В результате этого преобразования уравнение принимает вид
Если теперь обозначить
то уравнение станет квадратным уравнением:
Аналогично решается второе уравнение.
Решение похоже на решение симметрического уравнения
ax 4 + bx 3 + cx 2 + dx + e = 0 Ӏ : х 2
ax 2 +bx + c + 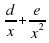
(ax 2 + 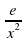
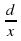
Делаем замену: у = bx + 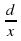
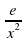
1) Решить уравнение: 2x 3 + 7x 2 + 7x + 2 = 0.
2(х 3 + 1) + 7х(х + 1) = 0
2(х + 1)(х 2 – х + 1) + 7х(х + 1) = 0
(х + 1)(2х 2 – 2х + 2 + 7х) = 0
(х + 1)( 2х 2 + 5х + 2) = 0
х + 1 = 0 и 2х 2 + 5х + 2 = 0
2) Решите уравнение: 2х 4 + 3х 3 – 16х 2 + 3х + 2 = 0
2х 4 + 3х 3 – 16х 2 + 3х + 2 = 0 Ӏ : х 2
2х 2 + 3х – 16 + 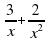
(2х 2 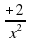
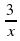
2(х 2 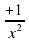
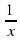
Пусть у = х + 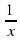
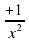
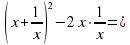
2(у 2 – 2) + 3у – 16 = 0
2х 2 – 5х + 2 = 0, х 0 х 2 + 4х + 1= 0, х 0
D = 25 – 16 = 9 D = 16 – 4 = 12
2(х 2 + ) – 5(х + 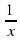
Пусть у = х + 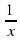
х + 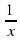
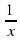
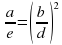
Задание: Решите уравнения:
4х 2 + 12х + = 47 (0,5; 2; )
5х 5 – 6х 4 – 79х 3 – 79х 2 – 6х + 5 = 0 (-1; ; 5)
Математика. Симметрические уравнения и примеры их решения.
Уравнения называются симметрическими уравнениями 3-й степени, если они имеют вид ах 3 + bx 2 + bх + a = 0.
Для того, чтобы успешно решать уравнения такого вида, полезно знать и уметь использовать следующие простейшие свойства возвратных уравнений:
Действительно, если сгруппировать в левой части слагаемые следующим образом: а(х 3 + 1) + bx(х + 1) = 0, то есть возможность вынести общий множитель, т.е. (х + 1)(ах 2 + (b – а)x + а) = 0, поэтому, х + 1 = 0 или ах 2 + (b – а)x + а = 0, первое уравнение и доказывает интересующее нас утверждение.
— У возвратного уравнения корней, равных нулю, нет.
в) При делении многочлена нечетной степени на (х + 1) частное является снова возвратным многочленом и это доказывается по индукции.
Уравнения называются симметрическими уравнениями 4-й степени, если они имеют вид ах 4 + bx 3 + сх 2 + bх + a = 0.
Алгоритм решения подобных уравнений таков:
б) С помощью группировки привести уравнение к виду: а(x 2 + 1/x 2 ) + b(x + 1/x) + c = 0.
в) Ввести новую неизвестную: t = (x + 1/x).
г) Решить в новых переменных полученное квадратное уравнение: аt 2 + bt + c – 2a = 0.
д) Сделать обратную подстановку.
Пример.
6х 4 – 5х 3 – 38x 2 – 5х + 6 = 0.
Решение.
6х 2 – 5х – 38 – 5/х + 6/х 2 = 0.
6(х 2 + 1/х 2 ) – 5(х + 1/х) – 38 = 0.
Вводим t: подстановка (x + 1/x) = t. Замена: (x 2 + 1/x 2 ) = t 2 – 2, имеем:
Вернемся к переменной х. После обратной замены решим два полученных уравнения:
Решить систему симметричных уравнений. Симметрические уравнения. Формула решения квадратного уравнения
Итак, для u получаем уравнение 
Попробуем найти корни уравнения исходной системы среди иррациональных чисел. Однако для этого придется проявить некоторую изобретательность: стандартная замена для симметрических систем здесь, очевидно не работает.
Возводя второе уравнение в куб, получим: Таким образом, по теореме Виета, и являются корнями квадратного уравнения Отсюда и Значит,
Для того, чтобы успешно решать уравнения такого вида, полезно знать и уметь использовать следующие простейшие свойства возвратных уравнений:
Действительно, если сгруппировать в левой части слагаемые следующим образом: а(х 3 + 1) + bx(х + 1) = 0, то есть возможность вынести общий множитель, т.е. (х + 1)(ах 2 + (b – а)x + а) = 0, поэтому,
х + 1 = 0 или ах 2 + (b – а)x + а = 0, первое уравнение и доказывает интересующее нас утверждение.
б) У возвратного уравнения корней, равных нулю, нет.
в) При делении многочлена нечетной степени на (х + 1) частное является снова возвратным многочленом и это доказывается по индукции.
х 3 + 2x 2 + 2х + 1 = 0.
| . | 1 | 2 | 2 | 1 |
| -1 | 1 | 2 – 1 = 1 | 2 – 1 = 1 | 1 – 1 = 0 |
х 3 + 2x 2 + 2х + 1 = (х + 1)(x 2 + х + 1) = 0.
Квадратное уравнение x 2 + х + 1 = 0 не имеет корней.
Алгоритм решения подобных уравнений таков:
б) С помощью группировки привести уравнение к виду:
а(x 2 + 1/x 2) + b(x + 1/x) + c = 0.
в) Ввести новую неизвестную: t = (x + 1/x).
г) Решить в новых переменных полученное квадратное уравнение:
аt 2 + bt + c – 2a = 0.
д) Сделать обратную подстановку.
6х 4 – 5х 3 – 38x 2 – 5х + 6 = 0.
6х 2 – 5х – 38 – 5/х + 6/х 2 = 0.
6(х 2 + 1/х 2) – 5(х + 1/х) – 38 = 0.
Вводим t: подстановка (x + 1/x) = t. Замена: (x 2 + 1/x 2) = t 2 – 2, имеем:
Вернемся к переменной х. После обратной замены решим два полученных уравнения:
Способы решения некоторых видов уравнений высших степеней
Примером такого уравнения может быть уравнение вида (х + а) 4 + (х + b) 4 = c.
(х + 3) 4 + (х + 1) 4 = 272.
Делаем подстановку, о которой говорилось выше:
t = x + (3 + 1)/2 = х + 2, после упрощения: х = t – 2.
(t – 2 + 3) 4 + (t – 2 + 1) 4 = 272.
(t + 1) 4 + (t – 1) 4 = 272.
Убрав скобки с помощью формул, получим:
t 4 + 4t 3 + 6t 2 + 4t + 1 + t 4 – 4t 3 + 6t 2 – 4t + 1 = 272.
2t 4 + 12t 2 – 270 = 0.
Второе уравнение корней не дает, а вот из первого имеем t = ±3.
Для решения подобных уравнений часто оказывается эффективным и метод разложения на множители левой части уравнения.
2. Уравнения вида (х + а)(х + b)(x + c)(x + d) = А, где а + d = c + b.
Методика решения подобных уравнений заключается в частичном раскрытии скобок, а затем введении новой переменной.
(х + 1)(х + 2)(x + 3)(x + 4) = 24.
Вычисляем: 1 + 4 = 2 + 3. Группируем скобки по парам:
((х + 1)(x + 4))((х + 2)(x + 3)) = 24,
(х 2 + 5х + 4)(х 2 + 5х + 6) = 24.
Сделав замену х 2 + 5х + 4 = t, имеем уравнение
t(t + 2) = 24, оно является квадратным:
После выполнения обратной замены, легко находим корни исходного уравнения.
Метод решения заключается в частичном раскрытии скобок, делении обеих частей на х 2 и решении совокупности квадратных уравнений.
Перемножив в левой части первые две и последние две скобки получим:
(х + 14 + 24/х)(х + 11 + 24/х) = 4. Заменой (х + 24/х) = t приходим к квадратному уравнению:
Произведя обратную замену х + 24/х = 10 или х + 24/х = 15, находим корни.
4. Решить уравнение (3х + 5) 4 + (х + 6) 3 = 4х 2 + 1.
Данное уравнение сразу трудно классифицировать и выбрать метод решения. Поэтому сначала преобразуем, используя разность квадратов и разность кубов:
((3х + 5) 2 – 4х 2) + ((х + 6) 3 – 1) = 0. Затем, после вынесения общего множителя, придем к простому уравнению:
(х + 5)(х 2 + 18х + 48) = 0.
f(x)/((х – 4) 2 (х + 2)) = q(x) или f(x) = (х – 4) 2 (х + 2)q(x).
Умножив первые две скобки, и приведя подобные слагаемые, получим: f(x) = (х 3 – 6x 2 + 32)q(х).
х 3 – 6x 2 + 32 – многочлен третьей степени, следовательно, q(x) – некоторое число из R (т. е. действительное). Пусть q(x) есть единица, тогда f(x) = х 3 – 6x 2 + 32.
Ответ: f(x) = х 3 – 6x 2 + 32.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Рациональные уравнения и неравенства
I. Рациональные уравнения.
Формула Виета для многочленов высших степеней.
Системы уравнений второй степени.
Метод введения новых неизвестных при решении уравнений и систем уравнений.
Решение симметрических систем уравнений.
Уравнения и системы уравнений с параметрами.
Графический метод решения систем нелинейных уравнений.
Уравнения, содержащие знак модуля.
Основные методы решения рациональных уравнений
Свойства равносильных неравенств.
Неравенства, содержащие неизвестное под знаком абсолютной величины.
Неравенства с параметрами.
Системы рациональных неравенств.
Графическое решение неравенств.
III. Проверочный тест.
P 1 (x) / Q 1 (x) + P 2 (x) / Q 2 (x) + … + P m (x) / Q m (x) = 0,
Если a=0; b0, то линейное уравнение решений не имеет.
Уравнение прямой имеет вид: y = ax + b.
Решение. Последовательно раскроем скобки, приведём подобные члены и найдём x: 2x – 3 + 4x – 4 = 5, 2x + 4x = 5 + 4 + 3,
Пример 1.2. Решить уравнение
2x – 3 + 2(x – 1) = 4(x – 1) – 7.
Решение. 2x + 2x – 4x = 3 +2 – 4 – 7, 0x = – 6.
2x + 3 – 6(x – 1) = 4(x – 1) + 5.
Решение. 2x – 6x + 3 + 6 = 4 – 4x + 5,
Системы линейных уравнений.
a 1 x 1 + a 2 x 2 + … + a n x n = b,
Система уравнений называется линейной, если все уравнения, входящие в систему, являются линейными. Если система из n неизвестных, то возможны следующие три случая:
система не имеет решений;
система имеет ровно одно решение;
система имеет бесконечно много решений.
Пример 2.4. решить систему уравнений
Решение. Решить систему линейных уравнений можно способом подстановки, который состоит в том, что какого-либо уравнения системы выражают одно неизвестное через другие неизвестные, а затем подставляют значение этого неизвестного в остальные уравнения.
Из первого уравнения выражаем: x= (8 – 3y) / 2. Подставляем это выражение во второе уравнение и получаем систему уравнений
X = (8 – 3y) / 2, 3(8 – 3y) / 2 + 2y = 7.Из второго уравнения получаем y = 2. С учётом этого из первого уравнения x = 1.Ответ: (1; 2).Пример 2.5. Решить систему уравнений
Решение. Система не имеет решений, так как два уравнения системы не могут удовлетворяться одновременно (из первого уравнения x + y = 3, а из второго x + y = 3,5).
Пример 2.6. решить систему уравнений
Решение. Система имеет бесконечно много решений, так как второе уравнение получается из первого путём умножения на 2 (т.е. фактически есть всего одно уравнение с двумя неизвестными).
Ответ: Бесконечно много решений.
Пример 2.7. решить систему уравнений
Решение. При решении систем линейных уравнений удобно пользоваться методом Гаусса, который состоит в преобразовании системы к треугольному виду.
Умножаем первое уравнение системы на – 2 и, складывая полученный результат со вторым уравнением, получаем – 3y + 6z = – 3. Это уравнение можно переписать в виде y – 2z = 1. Складывая первое уравнение с третьим, получаем 7y = 7, или y = 1.
Таким образом, система приобрела треугольный вид
Подставляя y = 1 во второе уравнение, находим z = 0. Подставляя y =1 и z = 0 в первое уравнение, находим x = 1.Ответ: (1; 1; 0).Пример 2.8. при каких значениях параметра a система уравнений
имеет бесконечно много решений? Решение. Из первого уравнения выражаем x:
Подставляя это выражение во второе уравнение, получаем
(a + 1)(– (a / 2)y + a / 2 +1) + 2ay = 2a + 4.
(a + 1)(a + 2 – ay) + 4ay = 4a + 8,
4ay – a(a + 1)y = 4(a + 2) – (a + 1)(a + 2),
ya(4 – a – 1) = (a + 2)(4 – a – 1),
Анализируя последнее уравнение, отметим, что при a = 3 оно имеет вид 0y = 0, т.е. оно удовлетворяется при любых значениях y. Ответ: 3.
Квадратные уравнения и уравнения, сводящиеся к ним.
Формула решения квадратного уравнения.
x 2 + (b / a)x + (c / a) = 0
выделим в левой части полный квадрат
x 2 + (b / a) + (c / a) = (x 2 + 2(b / 2a)x + (b / 2a) 2) – (b / 2a) 2 + (c / a) =
= (x + (b / 2a)) 2 – (b 2) / (4a 2) + (c / a) = (x + (b / 2a)) 2 – ((b 2 – 4ac) / (4a 2)).
Для краткости обозначим выражение (b 2 – 4ac) через D. Тогда полученное тождество примет вид
Возможны три случая:
По формуле разности квадратов выводим отсюда:
x 2 + (b / a)x + (c / a) = (x + (b / 2a) – (D / 2a))(x + (b / 2a) + (D / 2a)) =
= (x – ((-b + D) / 2a)) (x – ((– b – D) / 2a)).
Теорема: Если выполняется тождество
ax 2 + bx + c = a(x – x 1)(x – x 2),
В силу этой теоремы из, выведенного выше, тождества следует, что уравнение
x 2 + (b / a)x + (c / a) = 0,
а тем самым и уравнение ax 2 + bx + c = 0, имеет два корня:
Таким образом x 2 + (b / a)x + (c / a) = (x – x1)(x – x2).
Обычно эти корни записывают одной формулой:
если число D равно нулю (D = 0), то тождество
x 2 + (b / a)x + (c / a) = (x + (b / 2a)) 2 – (D / (4a 2))
Отсюда следует, что при D = 0 уравнение ax 2 + bx + c = 0 имеет один корень кратности 2: X 1 = – b / 2a
3) Если число D отрицательно (D 0, и потому выражение
x 2 + (b / a)x + (c / a) = (x + (b / 2a)) 2 – (D / (4a 2))
является суммой двух слагаемых, одно из которых неотрицательно, а другое положительно. Такая сумма не может равняться нулю, поэтому уравнение
x 2 + (b / a)x + (c / a) = 0
не имеет действительных корней. Не имеет их и уравнение ax 2 + bx + c = 0.
Таким образом, для решения квадратного уравнения следует вычислить дискриминант
Если D = 0, то квадратное уравнение имеет единственное решение:
Если D > 0, то квадратное уравнение имеет два корня:
Пример 3.10. Решить уравнение x 3 – 5x 2 + 6x = 0
Решение. Разложим левую часть уравнения на множители x(x 2 – 5x + 6) = 0,
отсюда x = 0 или x 2 – 5x + 6 = 0.
x 3 – 3x + 2 = 0. Решение. Перепишем уравнение, записав –3x = – x – 2x, x 3 – x – 2x + 2 = 0, а теперь группируемx(x 2 – 1) – 2(x – 1) = 0,(x – 1)(x(x + 1) – 2) = 0,x – 1 = 0, x 1 = 1,x 2 + x – 2 = 0, x 2 = – 2, x 3 = 1.Ответ: x 1 = x 3 = 1, x 2 = – 2.Пример 3.12. Решить уравнение7
Т.е. x 1 = 5; x 2 = 38 / 11.
Найденные значения удовлетворяют ОДЗ.
Ответ: x 1 = 0; x 2 = 5; x 3 = 38 / 11.
Пример 3.13. Решить уравнение x 6 – 5x 3 + 4 = 0
y 2 – 5y + 4 = 0, решив которое получаем Y 1 = 1; Y 2 = 4.
Таким образом, исходное уравнение эквивалентно совокупности
уравнений: x 3 = 1 или x 3 = 4, т. е. X 1 = 1 или X 2 = 3 4
Пример 3.14. Решить уравнение (x 3 – 27) / (x – 3) = 27
Решение. Разложим числитель на множители (по формуле разности кубов):
Научный руководитель: Кулабухов Сергей Юрьевич, кандидат физико-математических наук, педагог дополнительного образования МОУ ДОД ДТДиМ, г. Ростов-на-Дону.