Что такое симметричный отрезок
Осевая и центральная симметрия
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
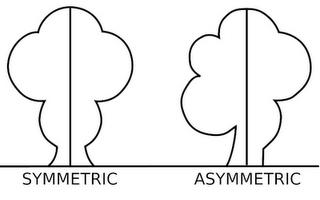
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
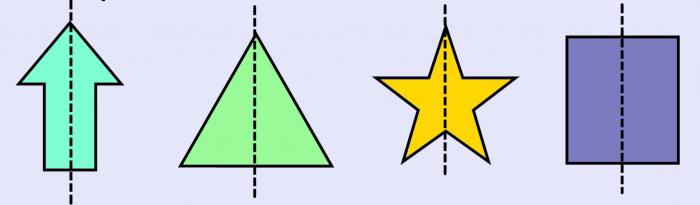
Рассмотрите фигуры с осевой и центральной симметрией.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.
Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 2. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
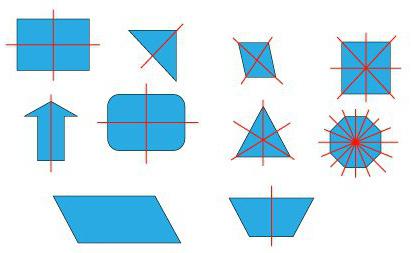
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.
Учебник Моро 4 класс 1 часть. Страница 63
Упражнения
283. Прочитай на странице 105, как связаны между собой числа при вычитании, и заполни таблицу.
284. Реши уравнения.
285. Вычисли и сделай проверку.
286. В магазин привезли хлеб. За день было продано 176 кг хлеба, после чего в магазине осталось на 145 кг хлеба меньше, чем продали. Сколько килограммов хлеба привезли?
1) 176 — 145 = 31 (кг) — масса оставшегося хлеба.
2) 176 + 31 = 207 (кг) — масса привезенного хлеба.
287. В зале 300 мест. Когда школьники заняли 8 полных рядов, в зале осталось 140 свободных мест. Сколько мест в каждом ряду, если все ряды одинаковые?
1) 300 — 140 = 160 (шт) — мест заняли школьники.
2) 160 : 8 = 20 (шт) — мест в одном ряду.
288. 1) Чему равна третья часть отрезка длиной 48 мм?
2) Начерти отрезов АВ. Начерти симметричный ему отрезок.
Отрезок CD (зелёный) симметричен отрезку AB (синий) относительно оси (красная прерывистая линия).
289. Вырази:
1) в миллиметрах:
9 см = 90 мм
80 см = 800 мм
2 м 25 см = 2 250 мм
2) в минутах:
9 ч = 60 • 9 = 540 мин
180 с = 180 : 60 = 3 мин
2 ч 25 мин = 60 • 2 + 25 = 120 + 25 = 145 мин
290. Реши:
Начерти отрезок, пятая часть которого равна 17 мм.
Длина отрезка составит 17 • 5 = 85 мм.
Задание на полях
1) 40 + 120 = 160 — значение зелёного круга.
2) 380 — 160 = 220 — значение синего треугольника.
Урок математики в 3-м классе по теме «Симметрия. Точки симметрии»
На стенде «к уроку» карточки:
1. Организационный момент
Учитель обращает внимание на стенд:
— Дети, начинаем урок с планирования нашей работы.
«:У одного философа по имени Буридан был осёл. Однажды, уезжая надолго, философ положил перед ослом две одинаковые охапки сена. Он поставил скамейку, а слева от скамейки и справа от нее на одинаковом расстоянии положил совершенно одинаковые охапки сена.
Рисунок 1 на доске:
Осел ходил от одной охапки сена к другой, но так и не решил, с какой охапки ему начать. И, в конце концов, умер с голоду».
— Почему осел так и не решил, с какой охапки сена ему начать?
— Что вы можете сказать про эти охапки сена?
(Охапки сена совершенно одинаковы, находились на одинаковом расстоянии от скамейки, значит, они симметричны).
2. Проведем небольшую исследовательскую работу.
— Возьмите лист бумаги (у каждого ребенка на парте лежит лист цветной бумаги), сложите его пополам. Проколите его ножкой циркуля. Разверните.
— Что у вас получилось? (2 симметричных точки).
— Как убедиться в том, что они действительно симметричны? (сложим лист, точки совпадают)
3. На доске:
Как вы думаете, симметричны ли данные точки? (нет). Почему? Как нам убедиться в этом?
Симметричны ли эти точки А и В?
Как мы можем это доказать?
(Измерить расстояние от прямой до точек)
Возвращаемся к нашим листочкам цветной бумаги.
— Измерьте расстояние от линии сгиба (оси симметрии) сначала до одной, а потом до другой точки (но сначала соедините их отрезком).
— Что вы можете сказать про эти расстояния?
— Найдите середину вашего отрезка.
(Является точкой пересечения отрезка АВ с осью симметрии)
4. Обращаем внимание на углы, образованные в результате пересечения отрезка АВ с осью симметрии. (Выясняем с помощью угольника, каждый ребенок работает на своем рабочем месте, один уч-ся на доске).
Вывод детей: отрезок АВ находится под прямым углом по отношению к оси симметрии.
— Сами того не ведая, мы сейчас с вами открыли математическое правило:
Если точки А и В симметричны относительно прямой или оси симметрии, то отрезок, соединяющий эти точки, находится под прямым углом, или перпендикулярен этой прямой. (Слово «перпендикулярен» выписано отдельно на стенде). Слово «перпендикулярен» произносим вслух хором.
5. Обратим внимание, как это правило написано у нас в учебнике.
Работа по учебнику.
Найдите симметричные точки, относительно прямой. Будут ли точки А и В симметричны относительно этой прямой?
6. Работа над новым материалом.
Поучимся строить точки, симметричные данным, относительно прямой.
Учитель учит рассуждать.
Чтобы построить точку, симметричную точке А, нужно перенести эту точку от прямой на то же расстояние вправо.
Далее уч-ся рассуждают у доски.
7. Будем учиться строить отрезки, симметричные данным, относительно прямой. Работа по учебнику.
Учащиеся рассуждают у доски.
8. Устный счет.
На этом мы закончим наше пребывание в Царстве «Геометрия» и проведем небольшую математическую разминку, побывав в царстве «Арифметика».
В то время, когда все работают устно, два учащиеся работают на индивидуальных досках.
А) Выполните деление с проверкой:
Б) Вставив нужные цифры, решите пример и проверьте:
Ответить на этот вопрос мы сможем, если выполним данные программы.
5) Найдите закономерность и помогите записать нужное число:
Далее проверяем решение примеров уч-ся на доске:
9. А сейчас немного отдохнем.
Послушаем «Лунную сонату» Бетховена. Минутка классической музыки. Уч-ся кладут голову на парту, закрывают глаза, слушают музыку.
10. Путешествие в царство алгебры.
Угадай корни уравнения и сделай проверку:
Уч-ся решают на доске и в тетрадях. Объясняют, как догадались.
а) Ася купила 5 бубликов по а рублей и 2 батона по b рублей. Сколько стоит вся покупка?
Составляем выражение: а*5 + b*2
Далее каждый составляет свою задачу по данному выражению, самостоятельно записывает ее решение.
Проверяем. Делимся мнениями.
12. Подведение итогов.
Итак, мы закончили наше путешествие в царство математики.
ВИДЫ СИММЕТРИИ
СИММЕТРИЯ ОТНОСИТЕЛЬНО ПРЯМОЙ (ОСЕВАЯ СИММЕТРИЯ)
Одна точка называются симметричной другой относительно прямой, если данная прямая проходит через середину отрезка, соединяющего эти точки, и перпендикулярна к этому отрезку. Каждая точка прямой а считается симметричной самой себе. Прямая называется осью симметрии фигуры если каждая точка фигуры симметрична относительно некоторой точки той же фигуры.
зеркальная симметрия
Геометрическая фигура называется симметричной относительно плоскости S, если для каждой точки этой фигуры может быть найдена другая точка этой же фигуры, так что отрезок, соединяющий эти точки, перпендикулярен плоскости S и делится этой плоскостью пополам. Плоскость S называется плоскостью симметрии.
Симметричные фигуры, предметы и тела не равны друг другу в узком смысле слова (например, левая перчатка или ботинок не подходит для правой руки или ноги и наоборот). Они называются зеркально равными.
центральная симметрия
Геометрическая фигура (или тело) называется симметричной относительно центра О, если для каждой точки этой фигуры может быть найдена другая точка этой же фигуры, так что отрезок, соединяющий эти точки, проходит через центр О и делится в этой точке пополам. Точка О называется центром симметрии.
поворотная симметрия (симметрия вращения)
При поворотной симметрии переход частей фигуры в новое положение или преобразование исходной фигуры происходит при повороте фигуры на определенный угол вокруг точки, которая называется центром поворота. Поворотная симметрия может рассматриваться на плоскости и в пространстве.
Тело (фигура) обладает симметрией вращения, если при повороте на угол 360°/n (n – целое число, например, 2, 3, 4 и т.д. до бесконечности) вокруг некоторой прямой (оси симметрии) оно полностью совпадает со своим начальным положением. При n = 2 мы имеем осевую симметрию.
симметрия подобия
Представляет собой своеобразный аналог предыдущих симметрий с той лишь разницей, что она связана с одновременным уменьшением или увеличением подобных частей фигуры и расстояний между ними. Простейшим примером такой симметрии являются матрешки.
переносная (трансляционная симметрия)
О такой симметрии говорят тогда, когда при переносе фигуры вдоль прямой на какое-то расстояние, либо расстояние, кратное этой величине, она совмещается сама с собой. Прямая, вдоль которой производится перенос, называется осью переноса.
примеры симметрии геометрических фигур
Разными видами симметрии могут обладать и плоские и объемные фигуры. Например, квадрат, прямоугольник, ромб имеют и центр симметрии и оси симметрии.
Окружность и круг имеют центр симметрии и бесконечно много осей симметрии. Объемные фигуры могут иметь центр симметрии, оси симметрии и обладать зеркальной симметрией.
Правильные многогранники своей симметрией с древних времён привлекали к себе внимание учёных, архитекторов, художников. Их по праву называют самыми симметричными из всех многогранников.
Подробно описал свойства правильных многогранников древнегреческий учёный Платон. Поэтому их называют телами Платона. Правильным многогранникам посвящена 13 книга “Начал” Евклида.
Очень симметричной фигурой является, например, куб. Центром симметрии куба является точка пересечения его диагоналей. Через центр симметрии проходят 9 осей симметрии. Плоскостей симметрии у куба также 9 и проходят они либо через противоположные ребра (6), либо через середины противоположных ребер (3).
Через центр симметрии проходят 9 осей симметрии. Плоскостей симметрии у куба также 9 и проходят они либо через противоположные ребра (6), либо через середины противоположных ребер (3).
Что такое симметрия и асимметрия?
Симметрия ассоциируется с гармонией и порядком. И не зря. Потому что на вопрос, что такое симметрия, есть ответ в виде дословного перевода с древнегреческого. И получается, что она означает соразмерность и неизменность. А что может быть упорядоченней, чем строгое определение местоположения? И что можно назвать более гармоничным, чем то, что строго соответствует размерам?
Что означает симметрия в разных науках?
Биология. В ней важной составляющей симметрии является то, что животные и растения имеют закономерно расположенные части. Причем в этой науке не существует строгой симметрии. Всегда наблюдается некоторая асимметрия. Она допускает то, что части целого не совпадают с абсолютной точностью.
Физика. Система тел и изменения в ней описываются с помощью уравнений. В них оказываются симметричные составляющие, что позволяет упростить все решение. Это выполняется благодаря поиску сохраняющихся величин.
Математика. Именно в ней в основном и дается разъяснение, что такое симметрия. Причем большее значение ей уделяется в геометрии. Здесь симметрия — это способность к отображению у фигур и тел. В узком смысле она сводится просто к зеркальному отображению.
Как определяют симметрию разные словари?
На вопрос, что такое симметрия, словарь Ожегова уже говорит об одинаковости в положении частей относительно точки, прямой или плоскости.
В словаре Ушакова упоминается еще и пропорциональность, а также полное соответствие двух частей целого друг другу.
Когда говорят об асимметрии?
Приставка «а» отрицает смысл основного существительного. Поэтому асимметрия означает то, что расположение элементов не поддается определенной закономерности. В ней отсутствует всякая неизменность.
В живой природе асимметрия играет важную роль. Причем она может быть как полезной, так и вредной. К примеру, сердце помещается в левую половину груди. За счет этого левое легкое существенно меньшего размера. Но это необходимо.
О центральной и осевой симметрии
В математике выделяют такие ее виды:
Что такое ось и центр симметрии? Это точка или прямая, относительно которой любой точке тела найдется другая. Причем такая, чтобы расстояние от исходной до получившейся делилось пополам осью или центром симметрии. Во время движения этих точек они описывают одинаковые траектории.
В ситуациях, когда необходимо найти центр симметрии, нужно поступать следующим образом. Если фигур две, то найти у них одинаковые точки и соединить их отрезком. Потом разделить пополам. Когда фигура одна, то помочь может знание ее свойств. Часто этот центр совпадает с точкой пересечения диагоналей или высот.
Какие фигуры являются симметричными?
Геометрические фигуры могут обладать осевой или центральной симметрией. Но это не обязательное условие, существует множество объектов, которые не обладают ею вовсе. К примеру, параллелограмм обладает центральной, но у него нет осевой. А неравнобедренные трапеции и треугольники не имеют симметрии совсем.
Если рассматривается центральная симметрия, фигур, обладающих ею, оказывается довольно много. Это отрезок и круг, параллелограмм и все правильные многоугольники с числом сторон, которое делится на два.
Центром симметрии отрезка (также круга) является его центр, а у параллелограмма он совпадает с пересечением диагоналей. В то время как у правильных многоугольников эта точка тоже совпадает с центром фигуры.
Если в фигуре можно провести прямую, вдоль которой ее можно сложить, и две половинки совпадут, то она (прямая) будет являться осью симметрии. Интересно то, сколько осей симметрии имеют разные фигуры.
К примеру, острый или тупой угол имеет только одну ось, которой является его биссектриса.
Если нужно найти ось в равнобедренном треугольнике, то нужно провести высоту к его основанию. Линия и будет осью симметрии. И всего одной. А в равностороннем их будет сразу три. К тому же, треугольник обладает еще и центральной симметрией относительно точки пересечения высот.
У круга может быть бесконечное число осей симметрии. Любая прямая, которая проходит через его центр, может исполнить эту роль.
Прямоугольник и ромб обладают двумя осями симметрии. У первого они проходят через середины сторон, а у второго совпадают с диагоналями.
Квадрат же объединяет предыдущие две фигуры и имеет сразу 4 оси симметрии. Они у него такие же, как у ромба и прямоугольника.