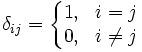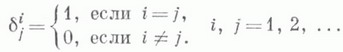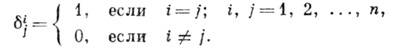Что такое символ кронекера

Символ Кронекера

Например, , но .

Содержание

Использование

Также может использоваться в соответствии со своим определением для записи разнообразных результатов или условий и в других контекстах.

История

Примечания

См. также

Полезное

Смотреть что такое «Символ Кронекера» в других словарях:

Символ Кронекера — Якоби — Не следует путать с Символ Кронекера. Символ Кронекера Якоби функция, используемая в теории чисел. Иногда называют символом Лежандра Якоби Кронекера или просто символом Кронекера. Является обобщением символов Лежандра и Якоби. Символ Лежандра… … Википедия

Символ Кронекера (значения) — Символ Кронекера математическое понятие, имеющее несколько значений. Символ Кронекера (дельта Кронекера) функция, используемая в линейной алгебре, тензорном анализе символ Кронекера Якоби теоретико числовая функция … Википедия

Символ Лежандра — Символ Лежандра функция, используемая в теории чисел. Введён французским математиком А. М. Лежандром. Символ Лежандра является частным случаем символа Якоби, который, в свою очередь, является частным случаем символа… … Википедия

Символ Якоби — Карл Густав Якоб Якоби (1804 1851). Символ Якоби теоретико числовая функция двух аргументов, введённая К. Якоби в 1837 году. Является квадратичным х … Википедия

КРОНЕКЕРА СИМВОЛ — простейший тензор 2 го ранга в n мерном пространстве, определяемый во всех системах координат равенствами К. с. введён Л. Кронекером (L. Kronecker) в 1866. Употребляется также обобщённый Кронекера символ, тензор более высокого ранга, компоненты к … Физическая энциклопедия

КРОНЕКЕРА СИМВОЛ — функция двух целочисленных переменных m и n, определяемая условием Введен Л. Кронекером (1866) КРОНЕНБЕРГ (Cronenberg) Дейвид (р. 1943) американский кинорежиссер. Признанный мастер фильмов ужасов. Фильм Сканнеры (1981), научно фантастический… … Большой Энциклопедический словарь

Кронекера символ — функция Δmn двух целочисленных переменных m и n, определяемая условием Введён Л. Кронекером (1866). * * * КРОНЕКЕРА СИМВОЛ КРОНЕКЕРА СИМВОЛ, функция двух целочисленных переменных m и n, определяемая условием Введен Л. Кронекером (1866) … Энциклопедический словарь

Источник

Кронекера символ

Символ Кронекера (или ‘дельта Кронекера) — функция двух переменных, которая равна 1, если они равны, и 0 в противном случае. Переменные обычно предполагаются целыми.

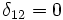
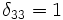
Например, , но .

Т.е. матрица составленная из элементов (δ_ij) является единичной.

Замечание: обычная практика обозначать той же буквой тензор после поднятия или опускания индекса не распространяется на дельту Кронекера! Это верно только в ортонормированных базисах, и, собственно говоря, является признаком, выделяющим ортонормированные базисы из всех.

История

Функция была введена Кронекером в 1866.

Примечания

См. также

Полезное

Смотреть что такое «Кронекера символ» в других словарях:

КРОНЕКЕРА СИМВОЛ — простейший тензор 2 го ранга в n мерном пространстве, определяемый во всех системах координат равенствами К. с. введён Л. Кронекером (L. Kronecker) в 1866. Употребляется также обобщённый Кронекера символ, тензор более высокого ранга, компоненты к … Физическая энциклопедия

КРОНЕКЕРА СИМВОЛ — функция двух целочисленных переменных m и n, определяемая условием Введен Л. Кронекером (1866) КРОНЕНБЕРГ (Cronenberg) Дейвид (р. 1943) американский кинорежиссер. Признанный мастер фильмов ужасов. Фильм Сканнеры (1981), научно фантастический… … Большой Энциклопедический словарь

Кронекера символ — функция Δmn двух целочисленных переменных m и n, определяемая условием Введён Л. Кронекером (1866). * * * КРОНЕКЕРА СИМВОЛ КРОНЕКЕРА СИМВОЛ, функция двух целочисленных переменных m и n, определяемая условием Введен Л. Кронекером (1866) … Энциклопедический словарь

Кронекера символ — функция δnm, зависящая от двух целочисленных аргументов n и m, которая определяется условием Пример применения К. с.: К. с. был введён Л. Кронекером (1866) … Большая советская энциклопедия

КРОНЕКЕРА СИМВОЛ — величина определяемая равенствами При К. с. имеет компонент, матрица к рых является единичной. К. с. введен Л. Кронекером (L. Kronecker, 1866). Обобщением К. с. является совокупность величин имеющих 2р целых (верхних и нижних) индексов, равных + … Математическая энциклопедия

Символ Кронекера — Якоби — Не следует путать с Символ Кронекера. Символ Кронекера Якоби функция, используемая в теории чисел. Иногда называют символом Лежандра Якоби Кронекера или просто символом Кронекера. Является обобщением символов Лежандра и Якоби. Символ Лежандра… … Википедия

Символ Кронекера (значения) — Символ Кронекера математическое понятие, имеющее несколько значений. Символ Кронекера (дельта Кронекера) функция, используемая в линейной алгебре, тензорном анализе символ Кронекера Якоби теоретико числовая функция … Википедия

Символ Лежандра — Символ Лежандра функция, используемая в теории чисел. Введён французским математиком А. М. Лежандром. Символ Лежандра является частным случаем символа Якоби, который, в свою очередь, является частным случаем символа… … Википедия

Символ Кронекера — У этого термина существуют и другие значения, см. Символ Кронекера (значения). Символ Кронекера (или дельта Кронекера) индикатор равенства элементов, формально: функция двух целых переменных, которая равна 1, если они равны, и 0 в противном… … Википедия

Источник

КРОНЕКЕРА СИМВОЛ

— величина определяемая равенствами

При К. с. имеет компонент, матрица к-рых является единичной. К. с. введен Л. Кронекером (L. Kronecker, 1866).

К. с. удобен в различных задачах тензорного исчисления. Напр., определитель

Лит.:[1] Kronecker L., Vorlesungen fiber die Theorie der Determinanten, Lpz., 1903. Л. Я. Купцов.

Полезное

Смотреть что такое «КРОНЕКЕРА СИМВОЛ» в других словарях:

КРОНЕКЕРА СИМВОЛ — простейший тензор 2 го ранга в n мерном пространстве, определяемый во всех системах координат равенствами К. с. введён Л. Кронекером (L. Kronecker) в 1866. Употребляется также обобщённый Кронекера символ, тензор более высокого ранга, компоненты к … Физическая энциклопедия

КРОНЕКЕРА СИМВОЛ — функция двух целочисленных переменных m и n, определяемая условием Введен Л. Кронекером (1866) КРОНЕНБЕРГ (Cronenberg) Дейвид (р. 1943) американский кинорежиссер. Признанный мастер фильмов ужасов. Фильм Сканнеры (1981), научно фантастический… … Большой Энциклопедический словарь

Кронекера символ — функция Δmn двух целочисленных переменных m и n, определяемая условием Введён Л. Кронекером (1866). * * * КРОНЕКЕРА СИМВОЛ КРОНЕКЕРА СИМВОЛ, функция двух целочисленных переменных m и n, определяемая условием Введен Л. Кронекером (1866) … Энциклопедический словарь

Кронекера символ — функция δnm, зависящая от двух целочисленных аргументов n и m, которая определяется условием Пример применения К. с.: К. с. был введён Л. Кронекером (1866) … Большая советская энциклопедия

Символ Кронекера — Якоби — Не следует путать с Символ Кронекера. Символ Кронекера Якоби функция, используемая в теории чисел. Иногда называют символом Лежандра Якоби Кронекера или просто символом Кронекера. Является обобщением символов Лежандра и Якоби. Символ Лежандра… … Википедия

Символ Кронекера (значения) — Символ Кронекера математическое понятие, имеющее несколько значений. Символ Кронекера (дельта Кронекера) функция, используемая в линейной алгебре, тензорном анализе символ Кронекера Якоби теоретико числовая функция … Википедия

Символ Лежандра — Символ Лежандра функция, используемая в теории чисел. Введён французским математиком А. М. Лежандром. Символ Лежандра является частным случаем символа Якоби, который, в свою очередь, является частным случаем символа… … Википедия

Символ Кронекера — У этого термина существуют и другие значения, см. Символ Кронекера (значения). Символ Кронекера (или дельта Кронекера) индикатор равенства элементов, формально: функция двух целых переменных, которая равна 1, если они равны, и 0 в противном… … Википедия

Источник

Дельта Кронекера

Дельта Кронекера естественным образом появляется во многих областях математики, физики и инженерии как средство компактного выражения своего определения, приведенного выше.

Ограничение на положительные или неотрицательные целые числа является обычным явлением, но фактически дельта Кронекера может быть определена на произвольном множестве.

Содержание

Свойства [ править ]

Удовлетворяются следующие уравнения:

Следовательно, матрицу δ можно рассматривать как единичную матрицу.

δ n m = 1 N ∑ k = 1 N e 2 π i k N ( n − m ) <\displaystyle \delta _=<\frac <1>>\sum _^e^<2\pi i<\frac >(n-m)>>

Альтернативная нотация [ править ]

Цифровая обработка сигналов [ править ]

<\text>-\infty

Или, в более общем смысле, где:

Однако это только очень частный случай. В тензорном исчислении базисные векторы в конкретном измерении чаще нумеруются, начиная с индекса 1, а не индекса 0. В этом случае отношения не существует, и фактически дельта-функция Кронекера и функция единичной выборки действительно разные функции, которые случайно перекрываются в одном конкретном случае, когда индексы включают число 0, количество индексов равно 2, а один из индексов имеет нулевое значение. δ [ n ] ≡ δ n 0 ≡ δ 0 n <\displaystyle \delta [n]\equiv \delta _\equiv \delta _<0n>>

Функцию дискретной единичной выборки проще определить как:

δ [ n ] = < 1 n = 0 0 otherwise <\displaystyle \delta [n]=<\begin1&n=0\\0&<\text>\end>>

δ ( t ) = < ∞ t = 0 0 otherwise <\displaystyle \delta (t)=<\begin\infty &t=0\\0&<\text>\end>>

Свойства дельта-функции [ править ]

Дельта Кронекера обладает так называемым свойством просеивания, что для j ∈ ℤ :

Связь с дельта-функцией Дирака [ править ]

Эквивалентно, функция плотности вероятности f ( x ) распределения может быть записана с использованием дельта-функции Дирака как

Обобщения [ править ]

Если рассматривать его как тензор типа (1,1), тензор Кронекера можно записать в виде δ я
j с ковариантным индексом j и контравариантным индексом i :

Этот тензор представляет:

Определения обобщенной дельты Кронекера [ править ]

В терминах индексов обобщенная дельта Кронекера определяется как: [4] [5]

В терминах определителя p × p : [6]

Используя разложение Лапласа ( формула Лапласа ) определителя, она может быть определена рекурсивно : [7]

Когда p = n (размерность векторного пространства), в терминах символа Леви-Чивиты :

Свойства обобщенной дельты Кронекера [ править ]

Обобщенная дельта Кронекера может использоваться для антисимметризации :

Из приведенных выше уравнений и свойств антисимметричных тензоров мы можем вывести свойства обобщенной дельты Кронекера:

Уменьшение порядка путем суммирования индексов может быть выражено тождеством [8]

Используя как правило суммирования для случая p = n, так и связь с символом Леви-Чивиты, выводится правило суммирования символа Леви-Чивита :

Интегральные представления [ править ]

Гребень Кронекера [ править ]

Функция гребенки Кронекера с периодом N определяется (в нотации DSP ) как:

Интеграл Кронекера [ править ]

в то время как нормаль имеет направление

Источник

КРОНЕКЕРА СИМВОЛ

К. с. введён Л. Кронекером (L. Kronecker) в 1866. Употребляется также обобщённый Кронекера символ, тензор более высокого ранга, компоненты к-рого связаны с Леви-Чивиты символом

Полезное

Смотреть что такое «КРОНЕКЕРА СИМВОЛ» в других словарях:

КРОНЕКЕРА СИМВОЛ — функция двух целочисленных переменных m и n, определяемая условием Введен Л. Кронекером (1866) КРОНЕНБЕРГ (Cronenberg) Дейвид (р. 1943) американский кинорежиссер. Признанный мастер фильмов ужасов. Фильм Сканнеры (1981), научно фантастический… … Большой Энциклопедический словарь

Кронекера символ — функция Δmn двух целочисленных переменных m и n, определяемая условием Введён Л. Кронекером (1866). * * * КРОНЕКЕРА СИМВОЛ КРОНЕКЕРА СИМВОЛ, функция двух целочисленных переменных m и n, определяемая условием Введен Л. Кронекером (1866) … Энциклопедический словарь

Кронекера символ — функция δnm, зависящая от двух целочисленных аргументов n и m, которая определяется условием Пример применения К. с.: К. с. был введён Л. Кронекером (1866) … Большая советская энциклопедия

КРОНЕКЕРА СИМВОЛ — величина определяемая равенствами При К. с. имеет компонент, матрица к рых является единичной. К. с. введен Л. Кронекером (L. Kronecker, 1866). Обобщением К. с. является совокупность величин имеющих 2р целых (верхних и нижних) индексов, равных + … Математическая энциклопедия

Символ Кронекера — Якоби — Не следует путать с Символ Кронекера. Символ Кронекера Якоби функция, используемая в теории чисел. Иногда называют символом Лежандра Якоби Кронекера или просто символом Кронекера. Является обобщением символов Лежандра и Якоби. Символ Лежандра… … Википедия

Символ Кронекера (значения) — Символ Кронекера математическое понятие, имеющее несколько значений. Символ Кронекера (дельта Кронекера) функция, используемая в линейной алгебре, тензорном анализе символ Кронекера Якоби теоретико числовая функция … Википедия

Символ Лежандра — Символ Лежандра функция, используемая в теории чисел. Введён французским математиком А. М. Лежандром. Символ Лежандра является частным случаем символа Якоби, который, в свою очередь, является частным случаем символа… … Википедия

Символ Кронекера — У этого термина существуют и другие значения, см. Символ Кронекера (значения). Символ Кронекера (или дельта Кронекера) индикатор равенства элементов, формально: функция двух целых переменных, которая равна 1, если они равны, и 0 в противном… … Википедия

Источник