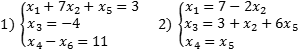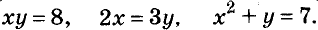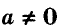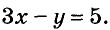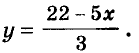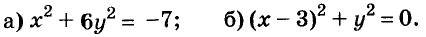Что такое система линейных уравнений

Системы линейных уравнений: основные понятия

— это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:

Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.

Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:

Если в каждом уравнении выбрать по одной разрешенной переменной, получим набор разрешенных переменных для всей системы уравнений. Сама система, записанная в таком виде, тоже будет называться разрешенной. Вообще говоря, одну и ту же исходную систему можно свести к разным разрешенным, однако сейчас нас это не волнует. Вот примеры разрешенных систем:

Обе системы являются разрешенными относительно переменных x ₁, x ₃ и x ₄. Впрочем, с тем же успехом можно утверждать, что вторая система — разрешенная относительно x ₁, x ₃ и x ₅. Достаточно переписать самое последнее уравнение в виде x ₅ = x ₄.

Теперь рассмотрим более общий случай. Пусть всего у нас k переменных, из которых r являются разрешенными. Тогда возможны два случая:

Так, в приведенных выше системах переменные x ₂, x ₅, x ₆ (для первой системы) и x ₂, x ₅ (для второй) являются свободными. Случай, когда есть свободные переменные, лучше сформулировать в виде теоремы:

Обратите внимание: это очень важный момент! В зависимости от того, как вы запишете итоговую систему, одна и та же переменная может быть как разрешенной, так и свободной. Большинство репетиторов по высшей математике рекомендуют выписывать переменные в лексикографическом порядке, т.е. по возрастанию индекса. Однако вы совершенно не обязаны следовать этому совету.

В чем смысл этой теоремы? Чтобы получить все решения разрешенной системы уравнений, достаточно выделить свободные переменные. Затем, присваивая свободным переменным разные значения, будем получать готовые решения. Вот и все — таким образом можно получить все решения системы. Других решений не существует.

Вывод: разрешенная система уравнений всегда совместна. Если число уравнений в разрешенной системе равно числу переменных, система будет определенной, если меньше — неопределенной.

И все бы хорошо, но возникает вопрос: как из исходной системы уравнений получить разрешенную? Для этого существует метод Гаусса.

Источник

Система линейных алгебраических уравнений

В данной публикации мы рассмотрим определение системы линейных алгебраических уравнений (СЛАУ), как она выглядит, какие виды бывают, а также как ее представить в матричной форме, в том числе расширенной.

Определение системы линейных уравнений

Система линейных алгебраических уравнений (или сокращенно “СЛАУ”) – это система, которая в общем виде выглядит так:

Индексы коэффициентов ( a_ij ) формируются следующим образом:

Виды СЛАУ

В зависимости от количества решений, СЛАУ может быть:

Матричная форма записи системы

СЛАУ можно представить в матричной форме:

Пример
Представим систему уравнений ниже в матричном виде:

Пользуясь формами выше, составляем основную матрицу с коэффициентами, столбцы с неизвестными и свободными членами.

Полная запись заданной системы уравнений в матричном виде:

Расширенная матрица СЛАУ

Для примера выше получается так:

– обозначение расширенной матрицы.

Источник

Системы линейных уравнений с примерами решений

Содержание:

Системы уравнений, как и отдельные уравнения, используют для решения сложных и необходимых задач. Системы уравнений бывают с двумя, тремя и более переменными. В этой главе вы ознакомитесь с простейшими системами двух уравнений с двумя переменными. Основные темы лекции:

Уравнения с двумя переменными

До сих пор мы рассматривали уравнение с одной переменной. Однако существуют задачи, решение которых приводит к уравнениям с двумя переменными.

Пример:

На 22 руб. купили несколько книжек по 5 руб. и географических карт — по 3 руб. Сколько купили книжек и карт?

Решение:

Пусть купили х книжки у карт. За книжки заплатили 5х руб., а за карты — 3у руб. Всего заплатили 22 руб., то есть, 5х + Зу = 22.

Это уравнение с двумя переменными. Приведём и другие примеры таких уравнений с двумя переменными:

Уравнение вида ах + by = с, где а, b, с — данные числа, называется линейным уравнением с двумя переменными х и у. Если

Примеры линейных уравнений:

два первых из них — уравнение первой степени с двумя переменными.

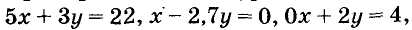
Каждая пара чисел, удовлетворяющая уравнение с двумя переменными, т. е. обращающая это уравнение в верное равенство, называется решением этого уравнения.

Обратите внимание: одно решение состоит из двух чисел, на первом месте записывают значение х, на втором — у. Корнями их не называют.

Чтобы найти решение уравнения с двумя переменными, следует подставить в уравнение произвольное значение первой неременной и, решив полученное уравнение, найти соответствующее значение второй переменной.

Для примера найдем несколько решений уравнения

Уравнение 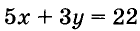также имеет бесконечно много решений, но сформулированную выше задачу удовлетворяет только одно из них: (2; 4).

Два уравнения с двумя переменными называют равносильными, если каждое из них имеет те же решения, что и другое. Уравнения, не имеющие решений, также считаются равносильными.

Для уравнения с двумя переменными остаются справедливыми свойства, сформулированные для уравнений с одной переменной.

Обе части уравнения с двумя переменными можно умножить или разделить на одно и то же число, отличное от нуля. Любой член такого уравнения можно перенести из одной части уравнения в другую, изменив его знак на противоположный. В результате получается уравнение, равносильное данному.

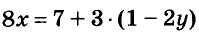
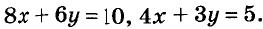
Например, уравнение можно преобразовать так: . Каждое из этих уравнений равносильно друг другу.

Иногда возникает потребность решить уравнение с двумя переменными во множестве целых чисел, то есть определить решения, являющиеся парами целых чисел. Способы решения таких уравнений определил древнегреческий математик Диофант (III в.), поэтому их называют диофантовыми уравнениями. Например, задача о книжках и картах сводится к уравнению 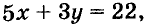где х и у могут быть только целыми (иногда натуральными) числами.

Переменную у из этого уравнения выразим через х:

Будем подставлять в равенство вместо х первые натуральные числа до тех пор, пока не получим целое значение переменной у. Это можно делать устно. Если х = 2, то у = 4. Других натуральных решений уравнение не имеет. Поэтому задача имеет единственное решение: 2 книги и 4 карты.

Пример:

Решение:

а) При любых значениях х и у значения выражения 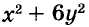не может быть отрицательным числом. Поэтому уравнение не имеет решений.

Пример:

Решение:

График линейного уравнения с двумя переменными

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Система линейных уравнений

Система линейных алгебраических уравнений (линейная система, также употребляются аббревиатуры СЛАУ, СЛУ) — система уравнений, каждое уравнение в которой является линейным — алгебраическим уравнением первой степени.

В классическом варианте коэффициенты при переменных, свободные члены и неизвестные считаются вещественными числами, но все методы и результаты сохраняются (либо естественным образом обобщаются) на случай любых полей, например, комплексных чисел.

Решение систем линейных алгебраических уравнений — одна из классических задач линейной алгебры, во многом определившая её объекты и методы. Кроме того, линейные алгебраические уравнения и методы их решения играют важную роль во многих прикладных направлениях, в том числе в линейном программировании, эконометрике.

Содержание

Соглашения и определения

Общий вид системы линейных алгебраических уравнений:

Матричная запись

СЛАУ может быть представлена и в матричной форме:

.

Здесь — это матрица системы, — столбец неизвестных, а — столбец свободных членов. Если к матрице приписать справа столбец свободных членов, то получившаяся матрица называется расширенной. Теорема Кронекера — Капелли устанавливает необходимое и достаточное условие совместности системы линейных алгебраических уравнений посредством свойств матричных представлений: система совместна тогда и только тогда, когда ранг её матрицы совпадает с рангом расширенной матрицы.

Эквивалентные системы линейных уравнений

Систему, эквивалентную данной, можно получить, в частности, заменив одно из уравнений на это уравнение, умноженное на любое отличное от нуля число. Эквивалентную систему можно получить также, заменив одно из уравнений суммой этого уравнения с другим уравнением системы. В общем, замена уравнения системы на линейную комбинацию уравнений даёт систему, эквивалентную исходной.

Методы решения

Прямые методы дают алгоритм, по которому можно найти точное решение систем линейных алгебраических уравнений. Итерационные методы основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений.

Некоторые прямые методы:

Итерационные методы устанавливают процедуру уточнения определённого начального приближения к решению. При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций. Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений. Суть этих методов состоит в том, чтобы найти неподвижную точку матричного уравнения

,

эквивалентного начальной системе линейных алгебраических уравнений. При итерации в правой части уравнения заменяется, например, в методе Якоби (метод простой итерации) приближение, найденное на предыдущем шаге:

.

Итерационные методы делятся на несколько типов, в зависимости от применяемого подхода:

Среди итерационных методов:

Источник

Что такое система линейных уравнений

Системой m линейных уравнений с n неизвестными называется система вида

где a_ij и b_i (i=1,…,m; b=1,…,n) – некоторые известные числа, а x₁,…,x_n – неизвестные. В обозначении коэффициентов a_ij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы.

Числа, стоящие в правых частях уравнений, b₁,…,b_m называются свободными членами.

Совокупность n чисел c₁,…,c_n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c₁,…,c_n вместо соответствующих неизвестных x₁,…,x_n.

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

Рассмотрим способы нахождения решений системы.

МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов

т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

или короче A∙X=B.

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.

Примеры. Решить системы уравнений.

Найдем матрицу обратную матрице A.

,

Таким образом, x = 3, y = – 1.

Выразим искомую матрицу X из заданного уравнения.

Из уравнения получаем .

Следовательно,

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы.

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A₁₁ элемента a₁₁, 2-ое уравнение – на A₂₁ и 3-е – на A₃₁:

Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

.

Далее рассмотрим коэффициенты при x₂:

Аналогично можно показать, что и .

Наконец несложно заметить, что

Таким образом, получаем равенство: .

Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

Примеры. Решить систему уравнений

Система имеет единственное решение, если Δ ≠ 0.

. Поэтому .

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

.

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x₁. Для этого второе уравнение разделим на а₂₁ и умножим на –а₁₁, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а₃₁ и умножим на –а₁₁, а затем сложим с первым. В результате исходная система примет вид:

Теперь из последнего уравнения исключим слагаемое, содержащее x₂. Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:

Отсюда из последнего уравнения легко найти x₃, затем из 2-го уравнения x₂ и, наконец, из 1-го – x₁.

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

Примеры: Решить системы уравнений методом Гаусса.

Вернувшись к системе уравнений, будем иметь

Выпишем расширенную матрицу системы и сведем ее к треугольному виду.

Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.

Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.

Вернемся к системе уравнений.

Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.

Таким образом, система имеет бесконечное множество решений.

Источник