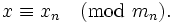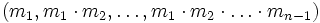Что такое система остаточных классов

Система счисления в остаточных классах (СОК)

Поиски новых путей повышения эффективности выполнения арифметических операций привели к заключению, что в рамках обычной позиционной системы счисления ускорения операций добиться сложно. Следует отметить, что позиционные системы счисления обладают существенным недостатком – наличием межразрядных связей, влияющих на способы реализации арифметических операций. В конечном итоге это приводит к усложнению аппаратуры и снижению быстродействия. Оказалось, что арифметика, в которой межразрядные связи отсутствовали бы, может быть построена на основе непозиционной системы счисления, в частности системы счисления в остаточных классах. В системе остаточных классов числа представляются остатками от деления на выбранную систему оснований и все рациональные операции могут выполняться параллельно над цифрами каждого разряда в отдельности. В то же время системе остаточных классов присущи некоторые недостатки: ограниченность действий этой системы полем целых положительных чисел, трудность определения соотношений чисел по величине, определения выхода результата операции из диапазона и некоторые другие.

причем образование цифр a_i осуществляется следующим образом:

где [] означает целую часть, то есть цифра i-го разряда a_i числа N есть наименьший положительный остаток от деления N на p_i.

Таким образом, в СОK в отличие от обобщенной позиционной системы счисления образование цифры каждого разряда производится независимо друг от друга. Очевидно, что a_i

=k_i + l_i + ,

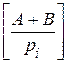
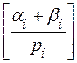
A + B = (k_i + l_i)p_i + .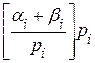

Подставляя полученные выражения в (6), получим:

В случае умножения

Аналогично сложению (A + B) получим:

= k_i l_i p_i + a_i l_i +b_i k_i + .

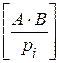
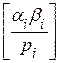
Пример. Сложить числа А = 23 и В = 48 в СОК.

Пусть основаниями системы являются p₁ = 3, p₂ = 5, p₃ = 7.

По выбранным основаниям числа А и В в СОК примут вид:

получим А + В = (2, 1, 1).

Легко проверить, что 23 + 48 = 71, а число 71 = (2, 1, 1) в СОК.

Пример. Умножить число А=14 на В=8 в СОК.

В соответствии с (4) получим:

Таким образом, А∙В = 122 = (1, 2, 1).

Охарактеризуем в общих чертах достоинства и недостатки введенной СОK.

Достоинства:

§ независимость образования разрядов числа, в силу чего каждый разряд несет информацию обо всем исходном числе, а не о промежуточном числе, получившемся в результате формирования младших разрядов (позиционная система счисления). Отсюда вытекает независимость разрядов числа друг от друга и возможность их параллельной обработки, что в свою очередь в дальнейшем позволяет вводить принципиально новые методы арифметического контроля. При введении дополнительного контрольного основания остаток, взятый по этому основанию, при его избыточности позволяет контролировать и исправлять ошибки в цифрах по рабочим основаниям;

§ малоразрядность остатков, представляющих число. Ввиду малого количества кодовых комбинаций открывается возможность построения табличной (не вычислительной) арифметики.

Недостатки:

§ невозможность визуального сопоставления чисел, так как внешняя запись числа не дает представления о его величине;

§ отсутствие простых признаков выхода результата операций за пределы [0,ρ];

§ ограниченность действий системы сферой целых положительных чисел;

§ получение во всех случаях точного результата исключает возможность приближенных вычислений, округлений.

Источник

Введение в модулярную арифметику

Для любой системы взаимно простых чисел p₁, … p_n, любое число X из диапазона [0; M), где M = p₁*p₂*…*p_n взаимооднозначно представимо в виде вектора (a₁, a₂, …, a_n), где a_i = X%p_i (здесь и далее «%» — операция взятия остатка от целочисленного деления X на p_i).
p₁, … p_n – модули системы
a₁, a₂, …, a_n – остатки (вычеты) числа по заданной системе модулей

Прямое преобразование

Прямое преобразование из позиционной системы счисления (обычно в двоичном виде) в систему счисления в остатках заключается в нахождении остатков от деления по каждому из модулей системы.

Пример: Пусть требуется найти представление числа X = 25 по системе модулей (3, 5, 7). X = (25%3, 25%5, 25%7) = (1, 0, 4).

Реализация нахождения вычета в микроэлектронике по заданному модулю строится на следующих свойствах вычетов:
(a+b) % p = (a%p + b%p)%p
(a*b) % p = (a%p * b%p)%p

Любое число X можно записать в виде X%p = (x_n-1*2 n-1 + x_n-2*2 n-2 + x₀*2 0 )%p = ((x_n-1)%p*2 n-1 %p) + ((x_n-2)%p*2 n-2 %p) + … + x₀%p)%p. Поскольку в данном случае x_n-1, … x₀ равны 0 или 1, то фактически нам требуется сложить вычеты вида (2 i %p).

Пример: пусть задано число 25 или в двоичной системе счисления 11001 и требуется найти остаток по модулю 7.
25%7 = (1*2 4 + 1*2 3 + 0*2 2 + 0* 1 + 1*2 0 )%7 = (2 4 %7 + 2 3 %7 + 1%7)%7 = (2 + 1 + 1)%7 = 4

Арифметические операции

Пример: пусть задана система модулей (3, 5, 7), то есть мы можем выполнять операции, результат которых не превышает 3*5*7 = 105. Умножим два числа 8 и 10.
8 = (8%3, 8%5, 8%7) = (2, 3, 1)
10 = (10%3, 10%5, 10%7) = (1, 0, 3)
8*10 = ((2*1)%3, (3*0)%5, (1*3)%7) = (2, 0, 3)
Проверяем
80 = (80%3, 80%5, 80%7) = (2, 0, 3)

Обратное преобразование

Способ, основанный на Китайской теореме об остатках, базируется на следующей идее:
X = (x₁, x₂, … x_n) = (x₁, 0, …, 0) + (0, x₂, …, 0) + … + (0, 0, …., x_n) = x₁*(1, 0, …, 0) + x₂*(0, 1, …, 0) + … + x_n*(0, 0, …, 1).
То есть для обратного преобразования требуется найти систему ортогональных базисов B1 = (1, 0, …, 0), B2 = (0, 1, …, 0), …, BN = (0, 0, …, 1). Эти вектора находятся один раз для заданного базиса, а для их поиска требуется решить уравнение вида: (M_i*b_i)%p_i = 1, где M_i = M/p_i, а b_i – искомое число. В этом случае позиционное представление B_i = M_i*b_i и
X = (x₁*(M₁*b₁) + x₂*(M₂*b₂) + … + x_n*(M_n*b_n))%M

Пример: пусть задана система модулей (3, 5, 7), найдем значения M_i и b_i (0 b₁ = 2
(21*b₂)%5 = 1 => b₂ = 1
(15*b₃)%7 = 1 => b₃ = 1
Теперь преобразуем какое-нибудь число в системе остаточных классов. Положим
X = (2, 3, 1) = (2*35*2 + 3*21*1 + 1*15*1)%105 = (140 + 63 + 15)%105 = 218%105 = 8

Минус этого метода заключается в том, что для обратного преобразования требуется умножение и сложение больших чисел (M₁, …, M_n), а так же операция взятия остатка по модулю большого числа M.

Источник

Система остаточных классов

Автор-составитель: Русачкова Елена

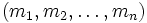
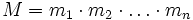
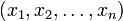
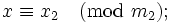
Представление числа в системе остаточных классов основано на понятии вычета и китайской теореме об остатках. СОК определяется набором взаимно простых модулей с произведением так, что каждому целому числу x из отрезка [0,M − 1] ставится в соответствие набор вычетов При этом китайская теорема об остатках гарантирует однозначность представления для чисел из отрезка [0,M − 1].

В СОК арифметические операции (сложение, вычитание, умножение, деление) выполняются покомпонентно, если про результат известно, что он является целочисленным и также лежит в [0,M − 1].

Недостатками СОК является возможность представления только ограниченного количества чисел, а также отсутствие эффективных алгоритмов для сравнения чисел, представленых в СОК. Сравнение обычно осуществляется через перевод аргументов из СОК в смешанную систему счисления по основаниям

Перевод чисел из СОК в десятичную систему счисления Формула перевода имеет вид:

A = a1*B1+a2*B2+…+an*Bn-r*P, где a1, …, an — представление числа А в СОК с основаниями p 1, p2, …, pn; P = p1* p2* …* pn;

r = 0,1,2,… (целые числа), причём r выбирают так, чтобы разность между левой и правой частью выражения была меньше P;

А = (2,4,6) в системе с основаниями: p1 = 3, p2 = 5, p3 = 7. P = p1*p2*p3 = 3*5*7 = 105.

Источник

Что такое система остаточных классов

Система остаточных классов позволяет существенно улучшить параметры вычислительных машин по сравнению с машинами, построенными на той же физико-технологической базе, но в позиционной системе счисления, а также получить новые, более прогрессивные конструктивные и структурные решения. [1]

Система остаточных классов дает возможность эффективно распараллелить арифметические операции, которые называются модульными. Кроме модульных операций часто выполняются и операции, носящие позиционный характер. [2]

Система остаточных классов допускает расширение или сокращение набора оснований без искажения при этом исходного числа. Например, для представления числа используется три основания — pi, Р2, Рз; тогда число изображается в виде A ( ai, а %, с з); если ввести новые основания — р4 и рз, то изображ: ение числа изменится и будет иметь вид А ( а, а %, сез, 4, б) — Аналогичным образом можно сократить набор оснований. Расширение оснований увеличивает диапазон и разрядность представления чисел, а сокращение — уменьшает. Образование остатков о производится независимо друг от друга. Последнее и определяет данную систему счисления как непозиционную; каждый разряд содержит в себе информацию обо всем числе. При выполнении сложения, вычитания и умножения каждая цифра результата зависит лишь от соответствующих цифр операндов. [3]

Система остаточных классов является фундаментальной для теории и практики машинной арифметики и позволяет ставить и решать новые задачи, недоступные для позиционных систем счисления. [4]

Система остаточных классов позволяет распараллелить весь процесс обработки данных, что подтверждает вывод многих авторов о том, что в настоящее время основное внимание уделяется способам параллельной обработки. [5]

Сочетание системы остаточных классов и нейронных сетей, которые дополняют друг друга, вызывает интерес по той причине, что легко реализовать принципы обменных операций между быстродействием, точностью и надежностью с целью создания отказоустойчивого нейрокомпьютера. [6]

Использование системы остаточных классов для кодирования числовой информации дает возможность эффективно распараллеливать алгоритмы выполнения элементарных арифметических операций автономных и неавтономных как П — задач, так и не П — задач, что и обеспечивает высокую производительность и надежность. В [4] показано, что в системе остаточных классов были созданы специализированные ЭВМ с уникальной для машин второго поколения производительностью 1 25 миллионов операций в секунду. [7]

Применение системы остаточных классов обеспечивает независимую и параллельную обработку каждого разряда числа, что и определяет структуру нейрокомпьютера. [8]

Кроме того, система остаточных классов является мощным методом повышения надежности. Показано [116], что система остаточных классов с двумя контрольными основаниями позволяет сохранить работоспособность машины при отказах двух элементов. Но и третий, и четвертый отказы не выводят машину из строя. СОК, является исключительно живучей, приближаясь в этом смысле к биологическим системам. К тому же следует отметить, что при переходе на БИС различия в сложности позиционных и непозиционных ЭВМ становятся незначительными. [9]

Основной теоретико-числовой базой системы остаточных классов ( СОК) является теория сравнений. Вопросы теории сравнений были разработаны выдающимся отечественным математиком П. Л. Чебы-шевым и изложены в его классическом труде Теория сравнений. Система остаточных классов дает нестандартное представление для чисел и используется для повышения эффективности операций над кодами в остатках. Дело в том, что в данной системе числа представляются своими остатками от деления на выбранную систему оснований и все рациональные операции могут выполняться параллельно над цифрами каждого разряда в отдельности. [10]

При выборе модулей системы остаточных классов необходимо учитывать вышеперечисленные свойства простых чисел. Так, при построении многоступенчатой системы остаточных классов можно рекомендовать для выбора модулей высших ступеней простые числа Мерсенна и Ферма, что упростит реализацию арифметических устройств и сократит время выполнения арифметической операции не только в табличном варианте, но и в регистровом варианте арифметических устройств. Кроме того, числа Мерсенна и Ферма можно использовать в качестве модулей системы СОК при байтовом кодировании информации. [11]

Сочетание корректирующих свойств системы остаточных классов и адаптивных свойств искусственных нейронных сетей позволяет реализовать непозиционный нейрокомпьютер с реконфигурируемой в динамике вычислительного процесса структурой. [12]

Для упрощения вычислений в системе остаточных классов желательно, чтобы модули р ( / г Е [1, ]) имели как можно более простое представление. Однако в полной мере экономия в вычислениях может быть достигнута лишь в том случае, когда обработка информации выполняется с помощью специальных вычислительных средств, эффективно представляющих модулярную арифметику. [13]

Нахождение обратных чисел в модульной арифметике (по сложению и умножению)

Модулярная арифметика

Модулярная арифметика часто изучается в школе как «арифметика часов». Если отсчитать 14 часов от 3 часов после полудня, то получится 5 часов утра следующего дня:

Это арифметика по модулю 12.

Обычная запись в модулярной арифметике

читается так: «а сравнимо с b по модулю n». Это соотношение справедливо для целых значений а, b и n ¹ 0, если, и только если

для некоторого целого k.

Отсюда, в частности, следует

Это читается как «n делит (а — b)».Если

то b называют вычетом числа а по модулю n.

Операцию нахождения вычета числа а по модулю n

называют приведением числа а по модулю n или приведением по модулю.

(3+ 14) mod 12 = 17 mod 12 = 5

число 5 является вычетом числа 17 по модулю 12.

Набор целых чисел от 0 до (n-1) называют полным набором вычетов по модулю п. Это означает, что для любого целого а(а>0) его вычет г по модулю n есть некоторое целое число в интервале от 0 до (n-1), определяемое из соотношения

r = a – k * n,

Например, для n =12 полный набор вычетов:

Обычно предпочитают использовать вычеты

но иногда полезны вычеты в диапазоне целых:

Заметим, что

Модулярная арифметика аналогична во многом обычной арифметике: она коммутативна, ассоциативна и дистрибутивна. Точнее говоря, целые числа по модулю n с использованием операций сложения и умножения образуют коммутативное кольцо при соблюдении законов ассоциативности, коммутативности и дистрибутивности.

Фактически мы можем либо сначала приводить по модулю n, а затем выполнять операции, либо сначала выполнять операции, а затем приводить по модулю n, поскольку приведение по модулю n является гомоморфным отображением из кольца целых в кольцо целых по модулю n:

(a + b) mod n = [a(mod n) + b(mod n )] mod n,

(a — b) mod n = [a(mod n) — b(mod n )] mod n,

(a * b) mod n = [a(mod n) * b(mod n )] mod n,

Криптография использует множество вычислений по модулю n, потому что задачи типа вычисления дискретных логарифмов и квадратных корней очень трудны. Кроме того, с вычислениями по модулю удобнее работать, потому что они ограничивают диапазон всех промежуточных величин и результата.

Для модуля n длиной k бит промежуточные результаты любого сложения, вычитания или умножения будут не длиннее 2k бит. Поэтому возведение в степень в модулярной арифметике можно выполнить без генерации очень больших промежуточных результатов.

Вычисление степени числа а по модулю n

можно выполнить как ряд умножений и делений. Существуют способы сделать это быстрее.

Система остаточных классов

Поскольку эти операции дистрибутивны, быстрее произвести возведение в степень как ряд последовательных умножений, выполняя каждый раз приведение по модулю. Это особенно заметно, если работать с длинными числами (200 бит и более).

Например, если нужно вычислить

не следует применять примитивный подход с выполнением семи перемножений и одного приведения по модулю громадного числа:

(a * a * a * a * a * a * a * a) mod n

Вместо этого выполняют три малых умножения и три малых приведения по модулю:

((a 2 mod n) 2 mod n) 2 mod n.

Тем же способом вычисляют

a 16 mod n = (((a 2 mod n) 2 mod n) 2 mod n) 2 mod n.

Вычисление

где х не является степенью 2, лишь немного сложнее. Двоичная запись числа х позволяет представить число х как сумму степеней 2:

x = 25₍₁₀₎ ® 1 1 0 0 1₍₂₎, поэтому 25 = 2 4 + 2 3 + 2 0

Тогда

a 25 mod n = (a * a 24 ) mod n = (a * a 8 * a 16 ) mod n = a * ((a 2 ) 2 ) 2 * (((a 2 ) 2 ) 2 ) 2 mod n = ((((a 2 * a) 2 ) 2 ) 2 * a) mod n.

При разумном накоплении промежуточных результатов потребуется только шесть умножений:

(((((((a 2 mod n) * a) mod n) 2 mod n) 2 mod n) 2 mod n) * a) mod n

Этот метод уменьшает трудоемкость вычислений до 1,5xk операций в среднем, где k-длина числа в битах [123].

Поскольку многие алгоритмы шифрования основаны на возведении в степень по модулю n, целесообразно использовать алгоритмы быстрого возведения в степень.

Источник

Что такое система остаточных классов

Сама сущность современных персональных компьютеров делает их зависящими от систем счисления и от правил, которые определяют связь между числами. Однако, остаточная система, или система остаточных классов, которая является темой этой статьи, представляет дополнительное отклонение от двоичной и десятичной систем чисел, чем последняя друг от друга, так как некоторые основные концепции, такие как использование фиксированных оснований (например, 10 или 2). В результате этих основных различий остаточная арифметика, которая является манипуляцией чисел, выраженных в системе остаточных классов, предлагает необычный набор характеристик. Например, остаточная арифметика обеспечивает возможность суммировать, вычитать или умножать в один этап, невзирая на протяженность чисел, не прибегая к промежуточным цифрам переноса или внутренним задержкам. Таким образом, скорее изменением в системе чисел, чем добавлением логических схем и оборудования, возможно в принципе заставить компьютер работать быстрее. К сожалению, остаточная арифметика также имеет атрибуты, которые являются затруднительными и убыточными настолько, что на практике технология использования не всегда возможна.

Рассмотрим некоторые свойства остаточной арифметики в сравнении с традиционными системами счисления. Для проведения сравнения рассмотрим свойства десятичной системы. Как будет видно далее, система остаточных чисел не имеет всех этих свойств.

Любое положительное целое число х может быть записано в виде

x = + (αn10n + αn-110n-1 + … + α110 + α0), (1)

где αi – это целые десятичные цифры в интервале [0, 9]. Очевидно, что десятичная система счисления не имеет пределов, т.е. любое целое число, невзирая на его значение, может быть выражено в системе. Более того, это уникальное представление, в котором каждое целое число имеет только одно представление. Однако, в отличие от других систем счисления, десятичное представление является безызбыточным, т.е. каждое сочетание αi цифр представляет число и два разных набора αi, не относящихся к одному и тому же числу.

Десятичная система имеет представление весового числа; каждая цифра αi умножается на постоянную величину в определяемой связи. В этом случае постоянная величина или вес – это 10i, а основания степени есть основание системы, то есть 10. Все веса, используемые в этой системе, – это степени одного и того же основания. Такие числовые системы называются системами с фиксированным основанием.

Введем некоторые отличительные свойства систем счисления.

Предел числовой системы определяется как интервал, над которым каждое целое число может быть представлено системой за неимением двух чисел с одним и тем же представлением. Очевидно, что десятичная система имеет неопределенные границы, однако в практике применяются усеченные системы чисел, потому что физические системы могут вместить только ограниченное число цифр. Так в компьютерах числовой предел определяется точно положением длины слова и типом используемой системы счисления.

Представление числа называется уникальным, если каждое число в системе имеет только одно представление. Например, двоичная система счисления, часто используемая в компьютерах, является уникальной. Однако многие обычно используемые системы чисел не являются уникальными. Например, десятичная система счисления, расширенная для включения отрицательных чисел, обычно имеет два представления для нуля: + 0 и – 0. Очевидно, что любая система с представлением знака и величины модуля также не уникальна. Существуют некоторые системы счисления, которые используют попеременные представления для всех чисел. Одна такая система была придумана для того, чтобы ограничить знак переноса до определенного числа цифр, в то время как другая используется для того, чтобы достичь коррекции ошибок в вычислениях. Основной ущерб этих представлений в том, что числа должны быть стандартной специфической формы для некоторых арифметических операций.

Система счисления будет избыточной, если существует меньше чисел, чем комбинаций цифр. Альтернативно разные комбинации могут относиться к одному и тому же числу. Очевидно, неуникальность подразумевает избыточность. Например, двоичная система с четными цифрами, добавленные в последнюю позицию цифр, имеет уникальное представление для каждого числа, и так как половина комбинаций запрещены, это представление является избыточным.

Также десятичная система, представленная в двоичном коде, как определено следующим уравнением, является избыточной:

x = (αn323 + αn222 + αn121 + αn020)10n + …+

+ (α0323 + α0222 + α0121 + α0020)100, (2)

где αi,j или 0 или 1 и 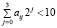для всех i. Избыточность проистекает из факта, что 6 из 16 двоичных комбинаций в каждой десятичной позиции не возникло.

Система счисления является позиционной, если существует набор позиций wi так, чтобы для любого числа х в системе, х может быть выражено в форме

, (3)

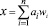
где αi – набор допустимых цифр. Если значения для wi это последовательные степени одного числа, то система счисления имеет фиксированное основание, например, основание 10 – для десятичной системы, основание 2 – для двоичной системы.

Позиционные системы счисления важны, потому что они обычно допускают подходящее сравнение величин двух чисел путем простой операции сравнения цифр в соответствующих позициях. Однако есть исключения, и не каждая позиционная система допускает определение сходного значения величины путем сравнения двух чисел. Например, рассмотрим следующую определяемую связь соотношением для системы счисления:

Источник