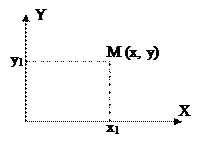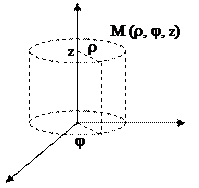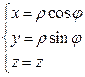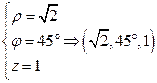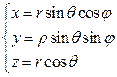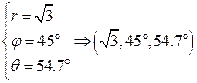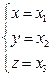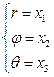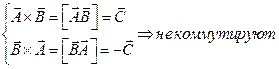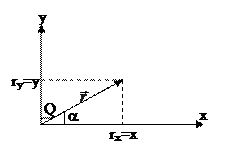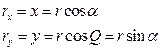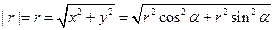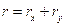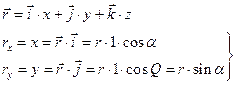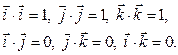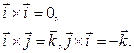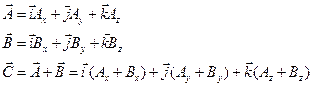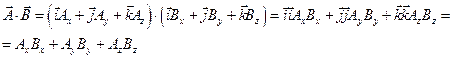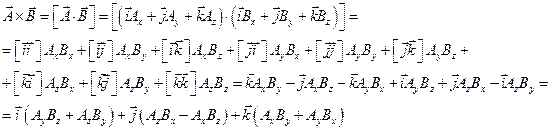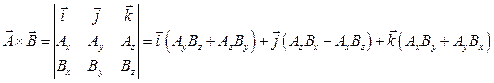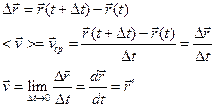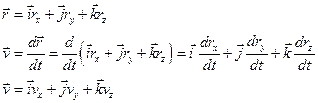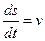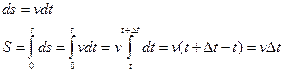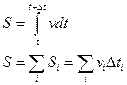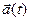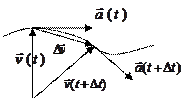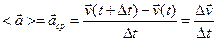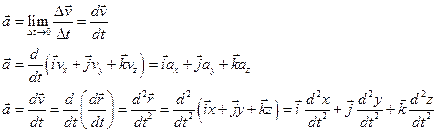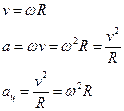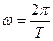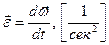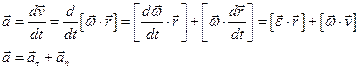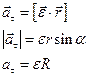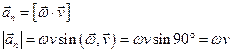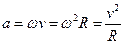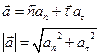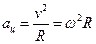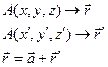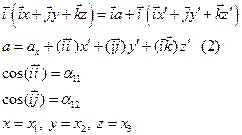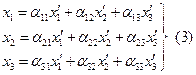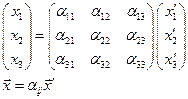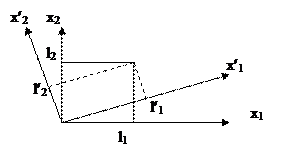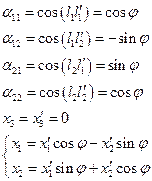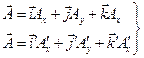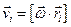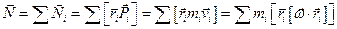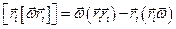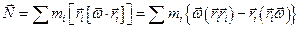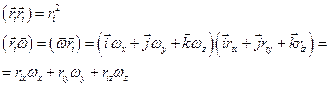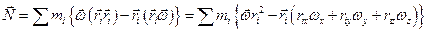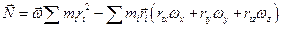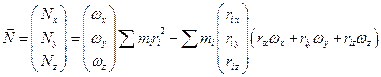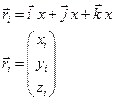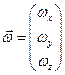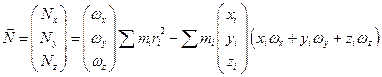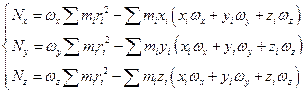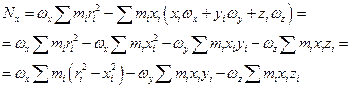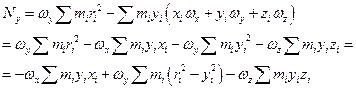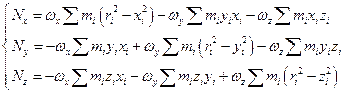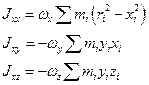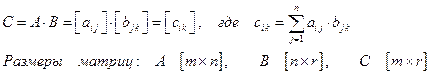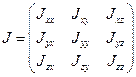Что такое система отсчета система координат

Система отсчёта

Математически движение тела (или материальной точки) по отношению к выбранной системе отсчёта описывается уравнениями, которые устанавливают, как изменяются с течением времени t координаты, определяющие положение тела (точки) в этой системе отсчёта. Эти уравнения называются уравнениями движения. Например, в декартовых координатах х, y, z движение точки определяется уравнениями , , .

В современной физике любое движение является относительным, и движение тела следует рассматривать лишь по отношению к какому-либо другому телу (телу отсчёта) или системе тел. Нельзя указать, например, как движется Луна вообще, можно лишь определить её движение, например, по отношению к Земле, Солнцу, звёздам и т. п.

Содержание

Другие определения

Иногда — особенно в механике сплошных сред и общей теории относительности — систему отсчёта связывают не с одним телом, а с континуумом реальных или воображаемых базовых тел отсчёта, которые задают также систему координат. Мировые линии тел отсчёта «заметают» пространство-время и задают в таком случае конгруэнцию, относительно которой можно рассматривать результаты измерений.

Относительность движения

Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта.

Движущиеся тела изменяют своё положение относительно других тел. Положение автомобиля, мчащегося по шоссе, изменяется относительно указателей на километровых столбах, положение корабля, плывущего в море недалеко от берега, меняется относительно береговой линии, а о движении самолёта, летящего над землей, можно судить по изменению его положения относительно поверхности Земли. Механическое движение — это процесс изменения относительного положения тел в пространстве с течением времени. Можно показать, что одно и то же тело может по-разному перемещаться относительно других тел.

Таким образом говорить о том, что какое-то тело движется, можно лишь тогда, когда ясно, относительно какого другого тела — тела отсчета, изменилось его положение.

Абсолютная система отсчёта

Часто в физике какую-то СО считают наиболее удобной (привилегированной) в рамках решения данной задачи — это определяется простотой расчётов либо записи уравнений динамики тел и полей в ней. Обычно такая возможность связана с симметрией задачи.

С другой стороны, ранее считалось, что существует некая «фундаментальная» система отсчёта, простота записи в которой законов природы выделяет её из всех остальных систем. Например, физики XIX в. считали что, система, относительно которой покоится эфир электродинамики Максвелла, является привилегированной, и поэтому она была названа Абсолютной Системой Отсчета (АСО). В современных представлениях никакой системы отсчёта, выделенной именно таким способом, не существует, так как законы природы, выраженные в тензорной форме, имеют один и тот же вид во всех системах отсчёта — то есть во всех точках пространства и во все моменты времени. Это условие — локальная пространственно-временная инвариантность — является одним из проверяемых оснований физики.

Источник

Кинематика. Система отсчета.

Любое физическое явление представляет собой последовательность событий. Для описания любого события необходимо иметь систему отсчета.

Система координат X, Y, Z, тело отсчета (материальная точка), с которым она связана, и часы для измерения времени образуют систему отсчета, относительно которой рассматривается движение тела.

Телом отсчета называют тело, по отношению к которому рассматривают изменение положения других тел в пространстве.

С телом отсчета сязывается система координат, которая представляет из себя точку отсчета. Для определения положения тела в пространстве в любой момент времени необходимо задать начало отсчета времени.

При решении каждой конкретной задачи выбирают удобную систему отсчета и удобную систему координат, а часы (идеальные) в каждой системе отсчета нужны лишь одни. Однако, тело отсчета, начало отсчета и направления координатных осей выбираются произвольно.

В отличие от геометрии, рассматривая физические явления, при произвольном построении координатной системы неявно подразумеваются два важных свойства пространства в вакууме: однородность и изотропность.

Однородность – это тождественность всех точек пространства. Это очень существенное свойство, которое позволяет пользоваться физикой. Законы физики одинаковы в разных точках Земли, как и в пределах Солнечной системы, что и позволяет помещать начало отсчета в любую удобную точку. Поворачивая координатную систему вокруг начала подразумевается, что от этого ничего не может измениться. Но это означает, что все направления, идущие от данной точки, тождественны по своим свойствам. Это и есть изотропность пространства.

Источник

Что такое система отсчета система координат

Система отсчёта — это совокупность тела отсчета, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точек или тел.

Математически движение тела (или материальной точки) по отношению к выбранной системе отсчёта описывается уравнениями, которые устанавливают, как изменяются с течением времени t координаты, определяющие положение тела (точки) в этой системе отсчёта. Эти уравнения называются уравнениями движения. Например, в декартовых координатах х, y, z движение точки определяется уравнениями

Движущиеся тела изменяют своё положение относительно других тел в пространстве с течением времени. Положение автомобиля, мчащегося по шоссе, изменяется относительно указателей на километровых столбах, положение корабля, плывущего в море недалеко от берега, меняется относительно береговой линии, а о движении самолёта, летящего над землей, можно судить по изменению его положения относительно поверхности Земли. Можно показать, что одно и то же тело при одном и том же движении может одновременно по-разному перемещаться относительно разных тел.

Абсолютная система отсчёта

Часто в физике какую-то СО считают наиболее удобной (привилегированной) в рамках решения данной задачи — это определяется простотой расчётов либо записи уравнений динамики тел и полей в ней. Обычно такая возможность связана с симметрией задачи.

С другой стороны, ранее считалось, что существует некая «фундаментальная» система отсчёта, простота записи в которой законов природы выделяет её из всех остальных систем. Например, физики XIX в. считали что, система, относительно которой покоится эфир электродинамики Максвелла, является привилегированной, и поэтому она была названа Абсолютной Системой Отсчета (АСО). В современных представлениях никакой системы отсчёта, выделенной именно таким способом, не существует, так как законы природы, выраженные в тензорной форме, имеют один и тот же вид во всех системах отсчёта — то есть во всех точках пространства и во все моменты времени. Это условие — локальная пространственно-временная инвариантность — является одним из проверяемых оснований физики.

Иногда абсолютной системой отсчета называют систему, связанную с реликтовым излучением, то есть инерциальную систему отсчета, в которой реликтовое излучение не имеет дипольной анизотропии.

Источник

Системы координат. Системы отсчета

Все механические процессы происходят в пространстве и времени. Это находит отражение в любом механическом законе.

Положение тела в пространстве может быть определено только по отношению к другим телам. Тело отсчета – тело (система неподвижных тел), которое служит для определения положения интересующего нас тела.

Кроме тела отсчета нужна система, которая обеспечивала бы «адреса» других тел. С этой целью вводится система координат. Система координат позволяет определить положение тела в пространстве. Но нужна еще совокупность тела отсчета, связанных с ним координат и синхронизирующих часов – это система отсчета.

Заметим, что удачный выбор системы координат существенно облегчает решение задачи. Рассмотрим основные типы систем координат:

1. Прямоугольная Декартова:

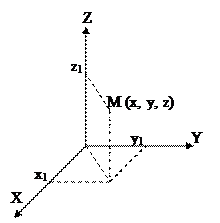
2. Цилиндрическая система координат:

Задание: Найти координаты точки (1,1,1) в цилиндрической системе координат.

3. Сферическая система координат:

Задание: Найти координаты точки (1,1,1) в сферической системе координат.

Формулы, связывающие координаты точки в одной системе отсчета с координатами в другой системе, называют формулами преобразования координат.

Скалярные, векторные величины. Действия над ними. Вычисление компонент вектора. Орты.

Для удобства координаты точки в любой системе координат будем обозначать одной буквой:

Вектор – направленный отрезок прямой, у которого один конец называется началом, а другой конец – концом. Модуль, направление, точка приложения, нулевой вектор.

Два вектора равны, если они имеют одинаковые модули и направление.

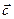
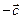
Противоположным вектору называют вектор .

Действия над векторами:

a. Правило треугольника ;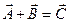

b. Правило прямоугольника;

Если при действии над векторами результат не изменяется при перестановке векторов, то говорят, что вектора обладают свойством коммутативности относительно этого действия.

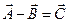
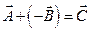
2. Разность векторов или ;

3. Умножение вектора на число ;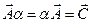

4. Скалярное произведение векторов:

Скалярным произведение векторов называют произведение модулей этих векторов на косинус угла между ними. Т.е. результат скалярного произведения – скаляр.

.

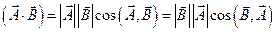
Обладает свойством коммутативности.

Пример: .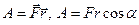

5. Векторное произведение:

В результате векторного произведения получается вектор, модуль которого равен произведению модулей перемножающихся векторов на синус угла между ними. Результирующий вектор направлен перпендикулярно плоскости перемножаемых векторов и направлен в сторону движения правого винта, если вращать его от первого вектора ко второму по кратчайшему пути.

Модуль вектора C равен площади параллелограмма, построенного на A и B.

Компоненты векторных величин.

Скалярное и векторное произведение орт:

Скалярные произведения одноименных орт равны 1, разноименных – 0.

Векторное произведение одноименных орт равно 0. Модуль векторного произведения разноименных орт равен 1.

Действия над векторами в координатной форме.

Компонент суммы двух векторов – сумма компонент слагаемых.

Радиус вектор – вектор, проведенный из начала координат в данную точку.

Перемещение и скорость в векторной и координатной формах.

Траектория – линия, вдоль которой движется тело.

Путь – расстояние вдоль траектории.

Перемещение – кратчайшее расстояние.

Вектором мгновенной скорости называют вектор, равный производной радиус-вектора по времени (направлен по касательной).

При прямолинейном движении .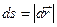

Абсолютное значение скорости (модуль):

В общем случае при прямолинейном движении

Если , то через параметры траектории:

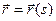
Ускорение в векторной и координатной формах.

вектор среднего ускорения (скорость изменения скорости)

Изменение линейной скорости по направлению (меняется только направление).

Вектор ускорения – вторая производная вектора перемещения по времени.

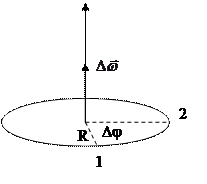
Кинематика вращательной точки. Угловая скорость.

Т – период (время одного оборота).

— линейная частота.

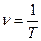
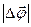
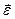
Модуль равен углу поворота и направлен по оси вращения так, что направление поворота отвечает правилу винта.

— угловое ускорение.

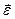
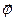
a) При равноускоренном движении вектор направлен в ту же сторону что и .

b) При равнозамедленном – в обратную.

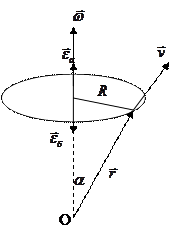
Вектора r, v и a называют естественными или полярными векторами.

Вектора 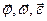— аксиальными.

Аксиальные вектора введены для объяснения физических процессов при вращательном движении. Они, так же как и полярные вектора подчиняются правилу сложения векторов.

Связь между линейными и угловыми величинами.

, r – радиус-вектор.

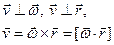
По определению векторного произведения .

a_n=a_ц – изменение скорости по направлению за единицу времени.

a_t – изменение скорости по модулю за единицу времени. При равномерном движении a_t=0.

Преобразование координат и компонент векторов.

Формулы, связывающие координаты точки в одной системе координат с координатами в другой называются преобразование координат.

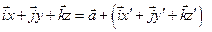(1)

Для определения компоненты x умножим скалярно (1) на i:

Тогда (2) запишем для случая a_x=0 (поворот):

Пример: Преобразование координат для двухмерного случая.

Значение скалярной величины определяется одним числом.

Значение вектора определяется тремя числами, которые называют компоненты вектора.

Более общее определение вектора:

Вектор – это упорядоченная совокупность трех чисел, зависящих от системы координат и преобразующихся при повороте системы отсчета так же, как преобразуются компоненты вектора.

При параллельном переносе компоненты вектора не изменяются:

Вектор тот же, но системы разные.

означает в координатной форме равенство компонент.

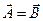
Величины, значения которых не изменяются при преобразованиях, называются инвариантами.

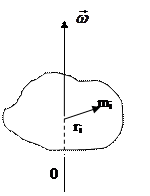
Вращение вокруг неподвижной оси.

Для точки m_i имеем:

Рассмотрим момент импульса относительно оси 0. Общий момент импульса равен:

— двойное векторное произведение.

Аналогично преобразуем N_z .

Введем инерциальные коэффициенты или моменты инерции:

, , .

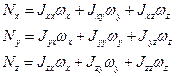
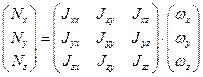
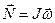
Здесь обозначения аналогичные.

Совокупность величин образует тензор инерции.

Тензор симметричный, т.е. 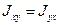и т.д. Таким образом тензор инерции определяется 6 числами.

Главные оси тензора инерции.

Симметричный тензор можно представить наглядно в виде эллипсоида, в данном случае эллипсоида инерции.

Тензор (второго ранга) – упорядоченная система 9 чисел, которые связывают два вектора.

Вектор (тензор первого ранга)– упорядоченная система трех чисел, которые преобразуются при изменении системы координат.

Скаляр (тензор нулевого ранга)– число, не изменяющееся при изменении системы координат.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник