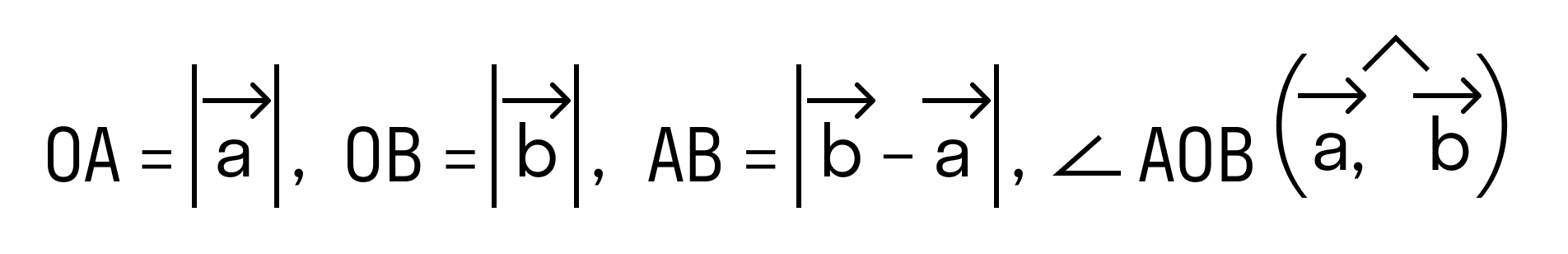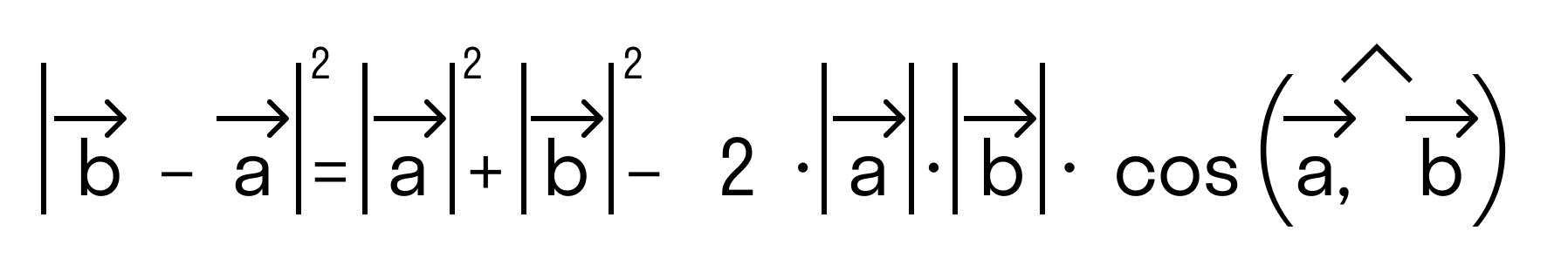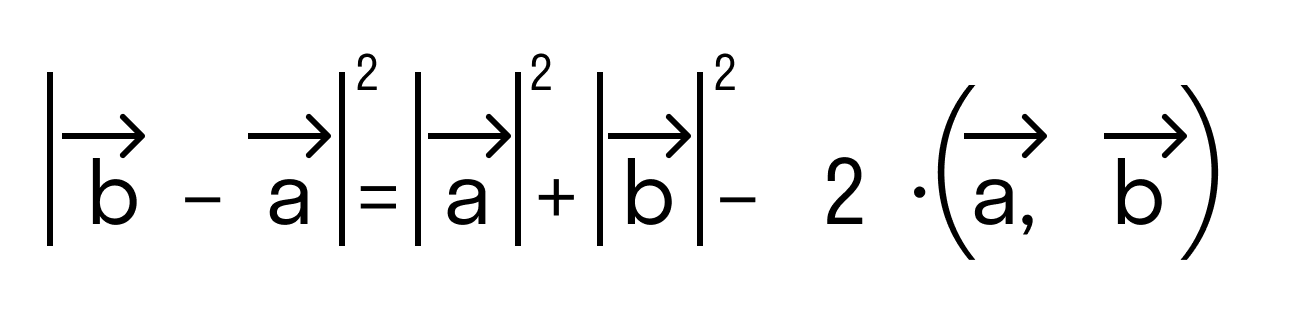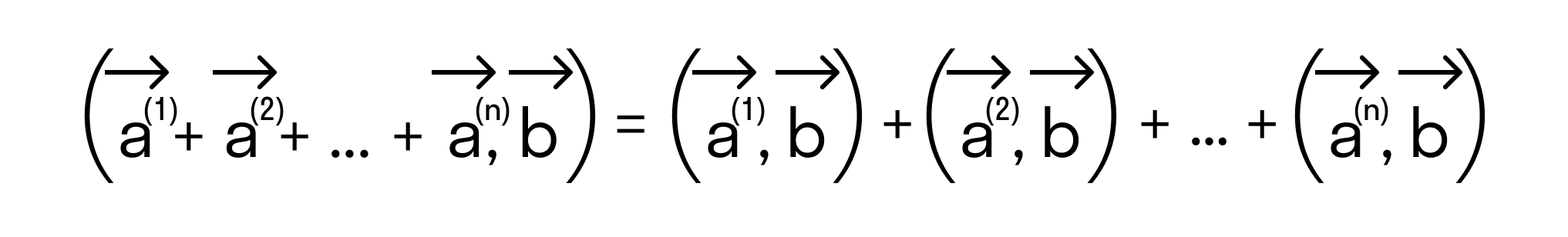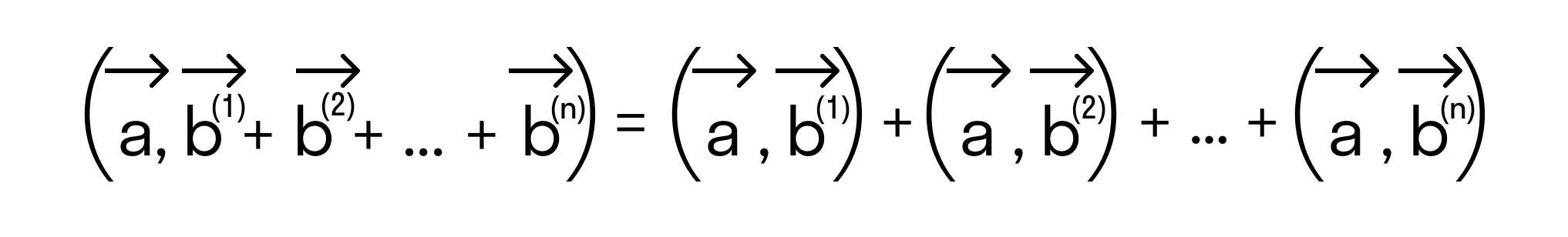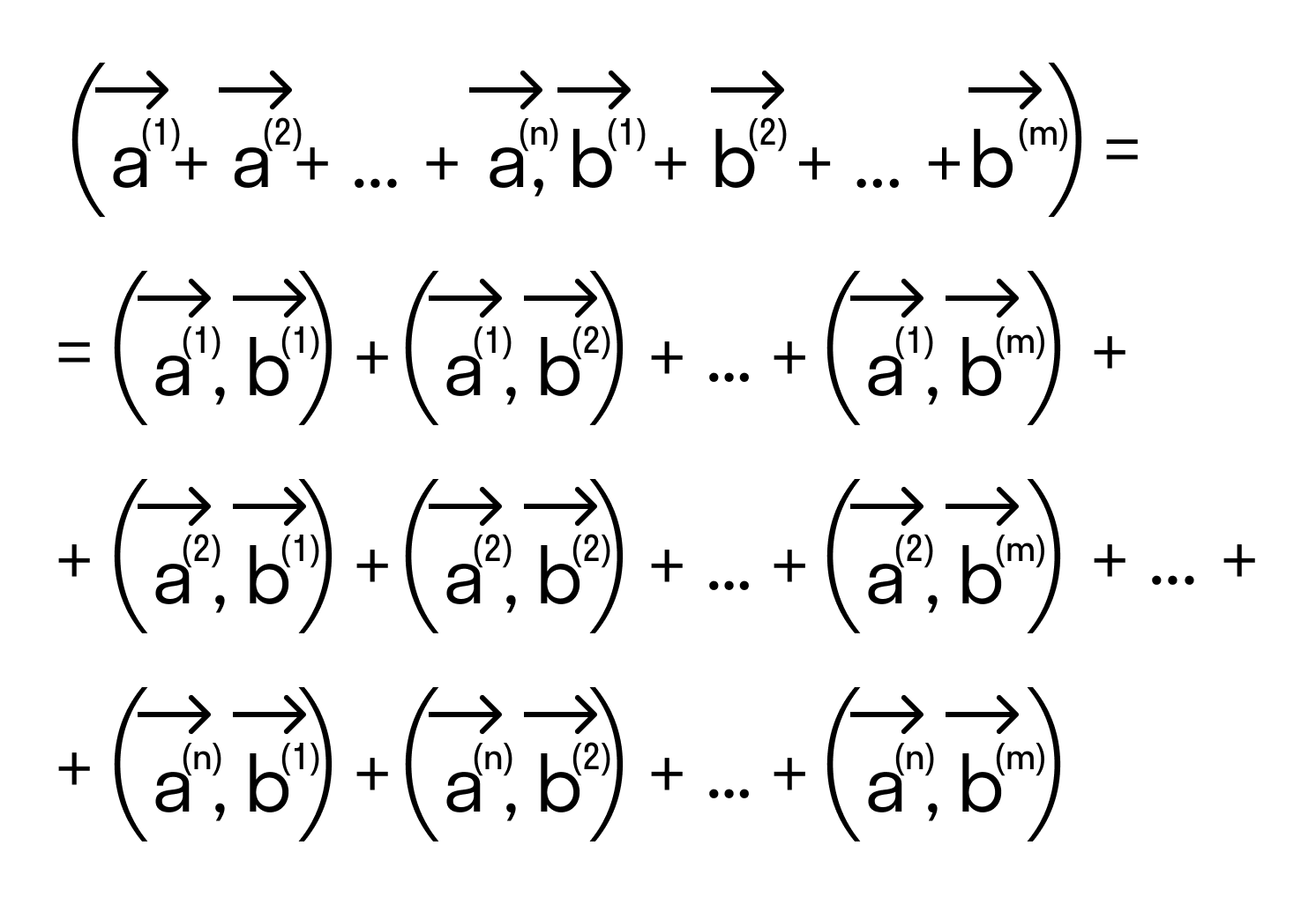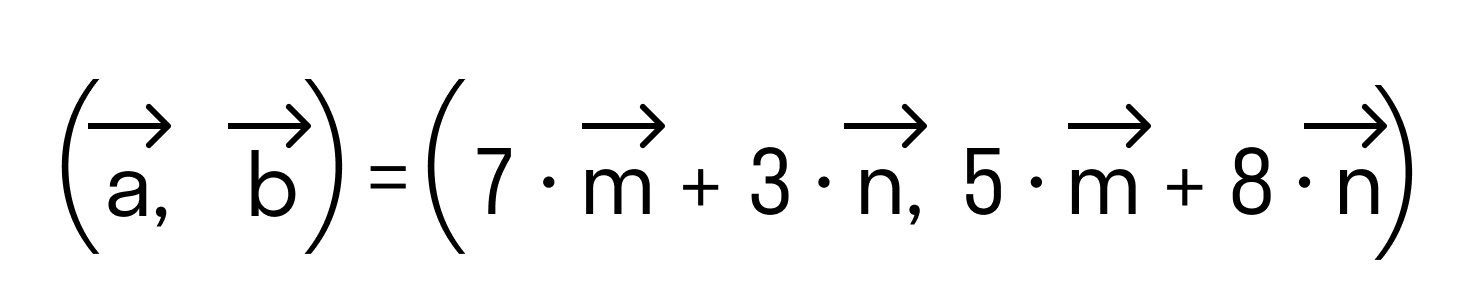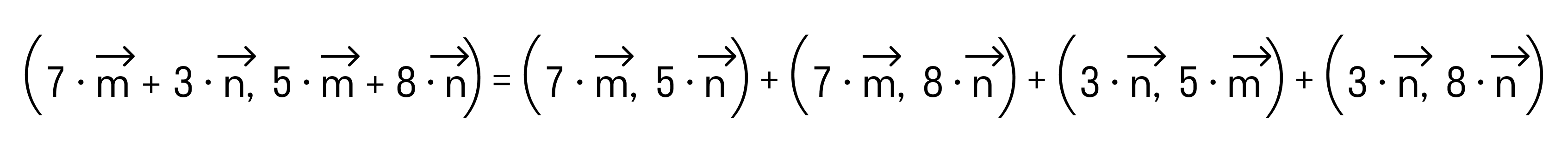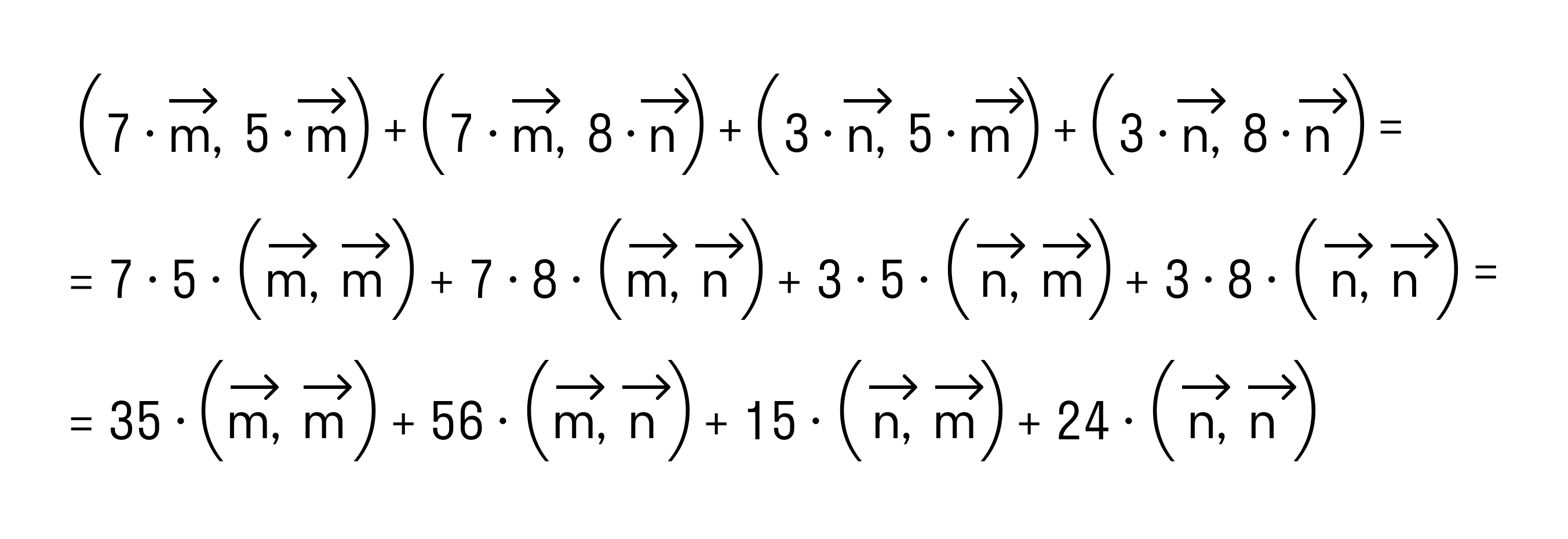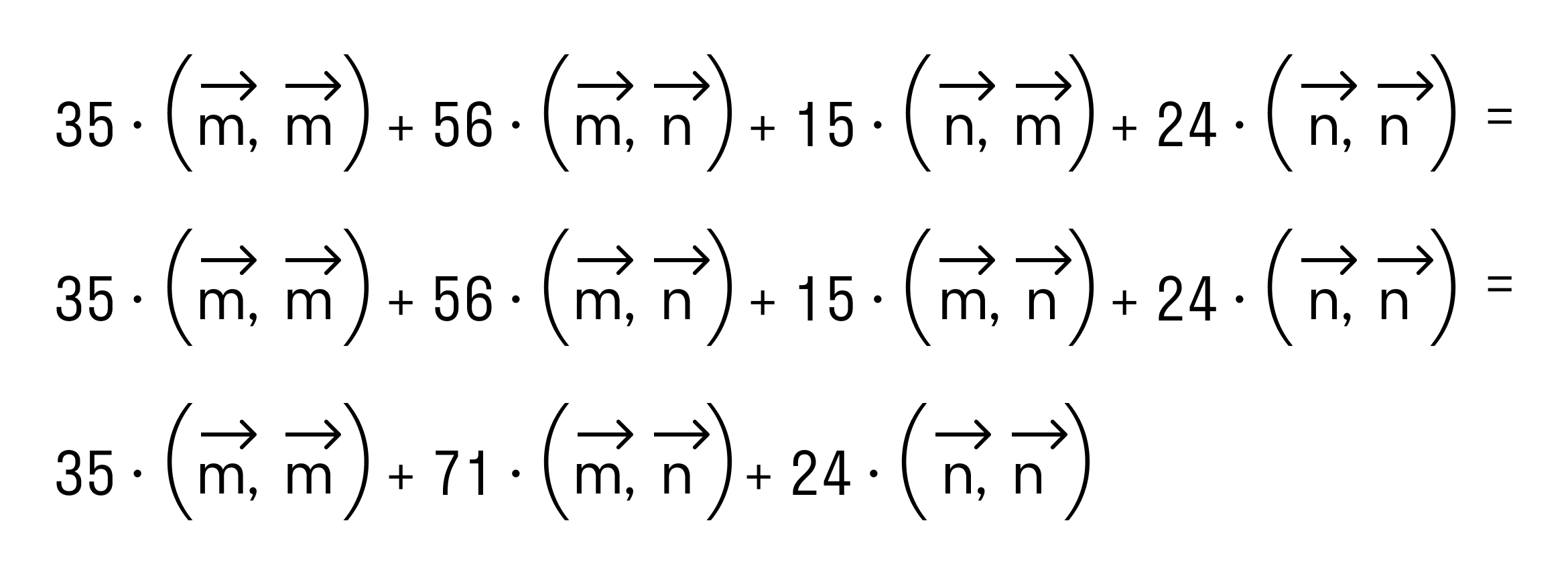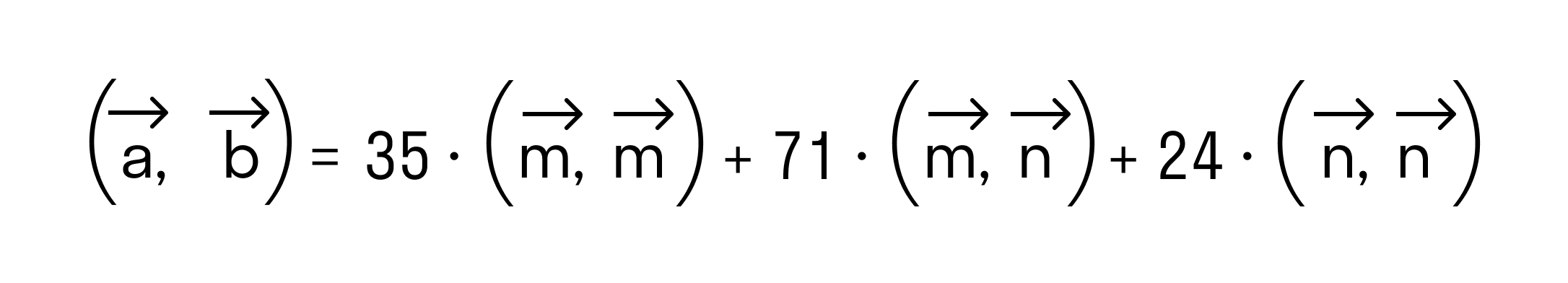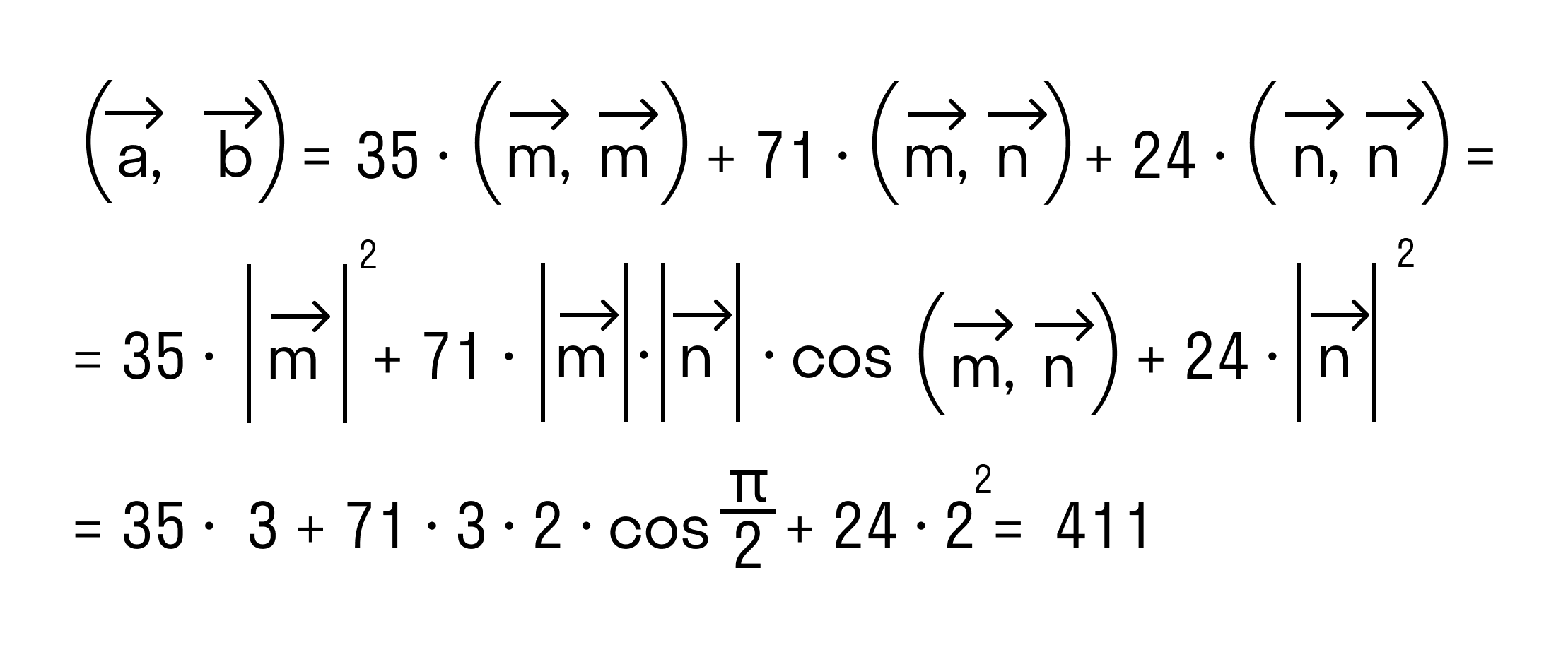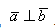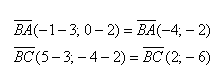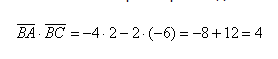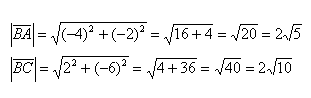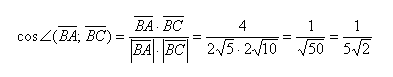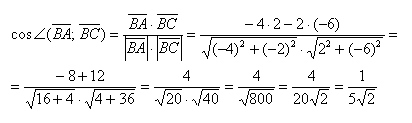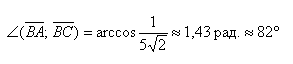Что такое скаляр в математике

Скаляр

Скаляр (от лат. scalaris — ступенчатый) — величина (возможно переменная, то есть функция), каждое значение которой может быть выражено одним числом (чаще всего подразумевается вещественное число).

При смене системы координат скаляр остаётся неизменным (инвариантным), в отличие, например, от компонентов вектора, которые могут быть разными у одного и того же вектора в разных системах координат.

Содержание

Примеры

Важно заметить, что понятие скаляра довольно сильно связано с контекстом. Так, в общепринятом контексте современной физики часть приведённых величин скалярными не являются. [1]

Ошибочные примеры

То же касается координаты тензора любой другой валентности (кроме нулевой).

Ещё одним примером величины, не являющейся, строго говоря, скаляром, является псевдоскаляр (хотя на практике иногда, исходя из соображений удобства или краткости, разграничения между скалярами и псевдоскалярами могут и не проводить, если это не существенно для изложения).

См. также

Примечания

Ссылки

Полезное

Смотреть что такое «Скаляр» в других словарях:

скаляр — а, м. scalaire <лат. scalaris ступенчатый < scalae лестница. Величина, в противоположность вектору, определяемая числовым значением без указания направления. БАС 1. Скалярный ая, ое. Скалярные величины. Уш. 1940: Лекс. СИС 1937: скаля/ры;… … Исторический словарь галлицизмов русского языка

скаляр — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] скаляр Величина, каждое значение которой может быть выражено одним (как правило, действительным) числом; по… … Справочник технического переводчика

СКАЛЯР — (от латинского scalaris ступенчатый) (скалярная величина), величина, каждое значение которой (в отличие от вектора) может быть выражено одним (действительным) числом, вследствие чего совокупность значений скаляра можно изобразить на линейной… … Современная энциклопедия

СКАЛЯР — (от лат. scalaris ступенчатый) (скалярная величина) величина, каждое значение которой (в отличие от вектора) может быть выражено одним (действительным) числом, вследствие чего совокупность значений скаляра можно изобразить на линейной шкале… … Большой Энциклопедический словарь

СКАЛЯР — СКАЛЯР, математическое число, имеющее только величину, в отличие от ВЕКТОРА, который имеет еще и направление. Масса и энергия являются скалярными величинами, тогда как вес и сила представлены векторными величинами … Научно-технический энциклопедический словарь

СКАЛЯР — величина, значение которой характеризуется действительным числом (без учета направления). Напр., температура, концентрация и т.п. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия

Скаляр — [scalar] величина, каждое значение которой может быть выражено одним (как правило, действительным) числом; по отношению к вектору, который можно рассматривать как многомерную величину, С. величина одномерная. Скалярная (числовая) функция одной… … Экономико-математический словарь

СКАЛЯР — величина, каждое значение которой может быть выражено одним действительным числом без учёта направления млн. другой какой либо оценки в выбранной системе единиц, напр. длина, площадь, объём, плотность, работа, температура и др … Большая политехническая энциклопедия

скаляр — а; м. [лат. scalaris ступенчатый] Матем. Величина, имеющая только числовое значение. ◁ Скалярный, ая, ое. С ые величины. * * * скаляр (от лат. scalaris ступенчатый) (скалярная величина), величина, каждое значение которой (в отличие от вектора)… … Энциклопедический словарь

Источник

Скаляры и векторы: что это такое

В физике используется много различных математических величин. Например, ускорение, скорость, сила, работа, мощность и так далее. Ученые делят эти величины на два типа: «скалярные» и «векторные». Что же означают эти типы и чем они отличаются?

Скаляр – это величина, которая описывается только значением. Значение этой величины выражает только число. Примеры скалярных величин: скорость, объем, масса, температура, мощность, энергия, время и т.д. Более о скорости читайте в учебнике по физике за 7 класс В.Г. Баряхтяра.

Вектор – это величина, которая имеет как значение, так и направление. Векторные величины важны при изучении движения. Некоторые примеры векторных величин: сила, скорость, ускорение, перемещение и импульс.

Вектор имеет и направление, и значение, а скаляр имеет только значение. Вы можете сказать, является ли величина вектором, просто если поймете, имеет ли эта величина направление.

Как нарисовать вектор?

Вектор нарисован в виде стрелки с головой и хвостом. Величину вектора часто описывают длиной стрелки. Стрелка указывает в направлении вектора.

Векторы обычно пишутся в виде жирных букв. Они также могут быть написаны в виде стрелки над буквой.

Пример вопросов: скаляр или вектор?

1) Футболист бежал со скоростью 15 км в час по направлению к концу зоны.

Это вектор, так как он представляет и значение (15 км/ч) и направление (по направлению к концу зоны).

2) Температура помещения составляет 15 градусов по Цельсию.

Это скаляр, направления нет.

3) Автомобиль разогнался на север со скоростью 4 м/с2 (четыре метра в секунду в квадрате).

Это вектор, поскольку он имеет как направление, так и величину. Мы также знаем, что ускорение – это векторная величина.

Источник

Скаляр

В общей и линейной алгебре скаляр — элемент основного поля. При этом, любой элемент линейного пространства может быть умножен на скаляр и результатом будет другой, коллинеарный элемент линейного пространства.

В тензорном исчислении скалярами являются тензоры валентности (0,0).

Содержание

Развитие понятия в физике

Важно заметить, что понятие скаляра довольно сильно связано с контекстом. Так, в общепринятом контексте современной физики часть приведённых величин скалярными не являются. [1]

В современной физике, подразумевающей пространственно-временной подход, под скаляром обычно имеется в виду скалярное поле, то есть пространственно-временной скаляр, лоренц-инвариантная величина, не меняющаяся при переходе от одной инерциальной системы отсчёта к другой (а в общей теории относительности и других метрических теориях гравитации — скаляр остается неизменным также и при переходе к неинерциальным системам отсчёта). В этом отличие от ньютоновской физики, где под скаляром понимается обычный скаляр обычного трёхмерного пространства (так, энергия в ньютоновском смысле — скаляр, а в пространственно-временном — лишь компонента четырёхмерного вектора).

Ошибочные примеры

То же касается координаты тензора любой другой валентности (кроме нулевой).

Ещё одним примером величины, не являющейся, строго говоря, скаляром, является псевдоскаляр (хотя на практике иногда, исходя из соображений удобства или краткости, разграничения между скалярами и псевдоскалярами могут и не проводить, если это не существенно для изложения).

Источник

Скалярное произведение векторов

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные определения

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

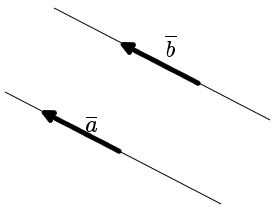
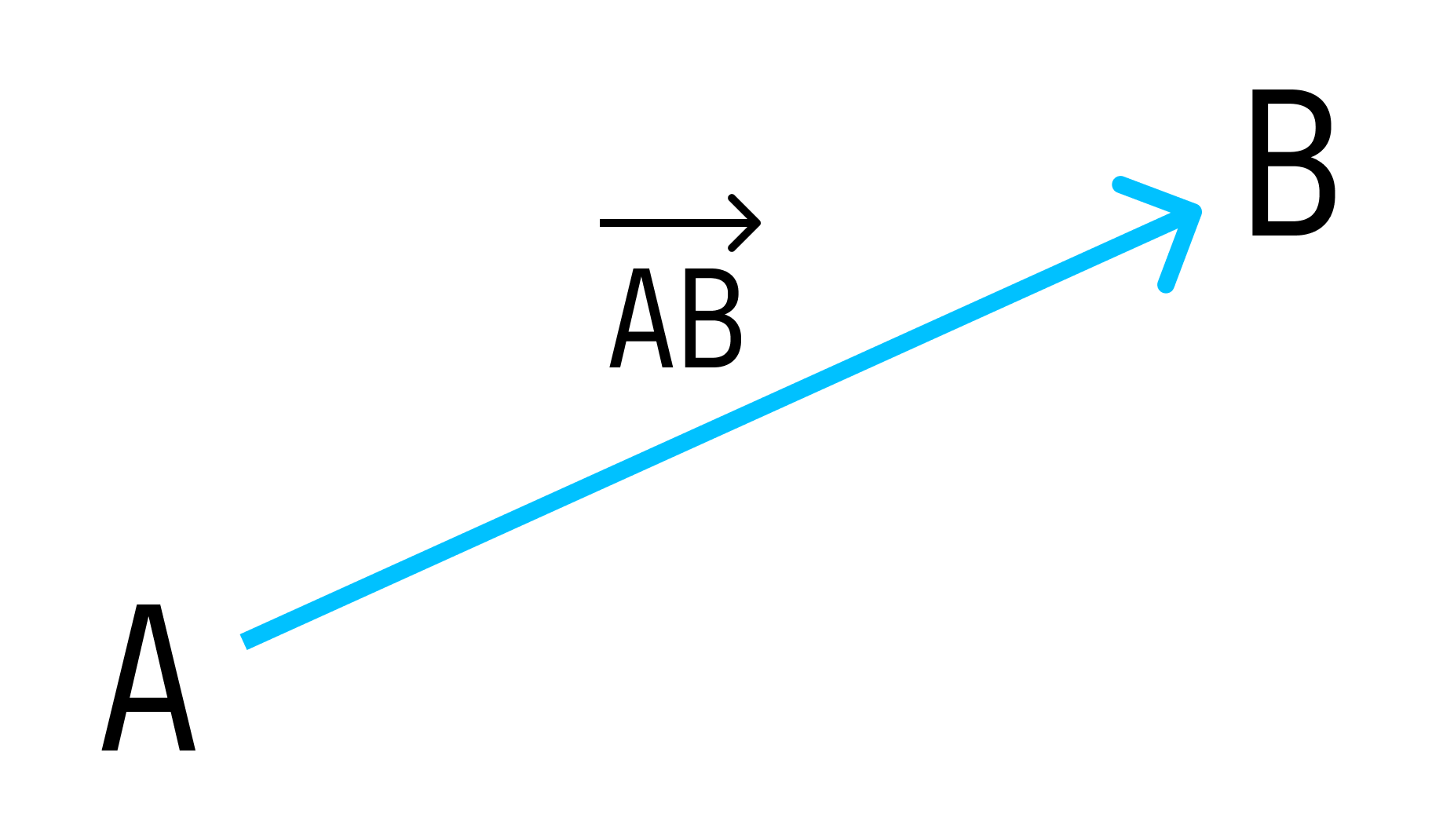
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.

Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.

Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.

Угол между векторами

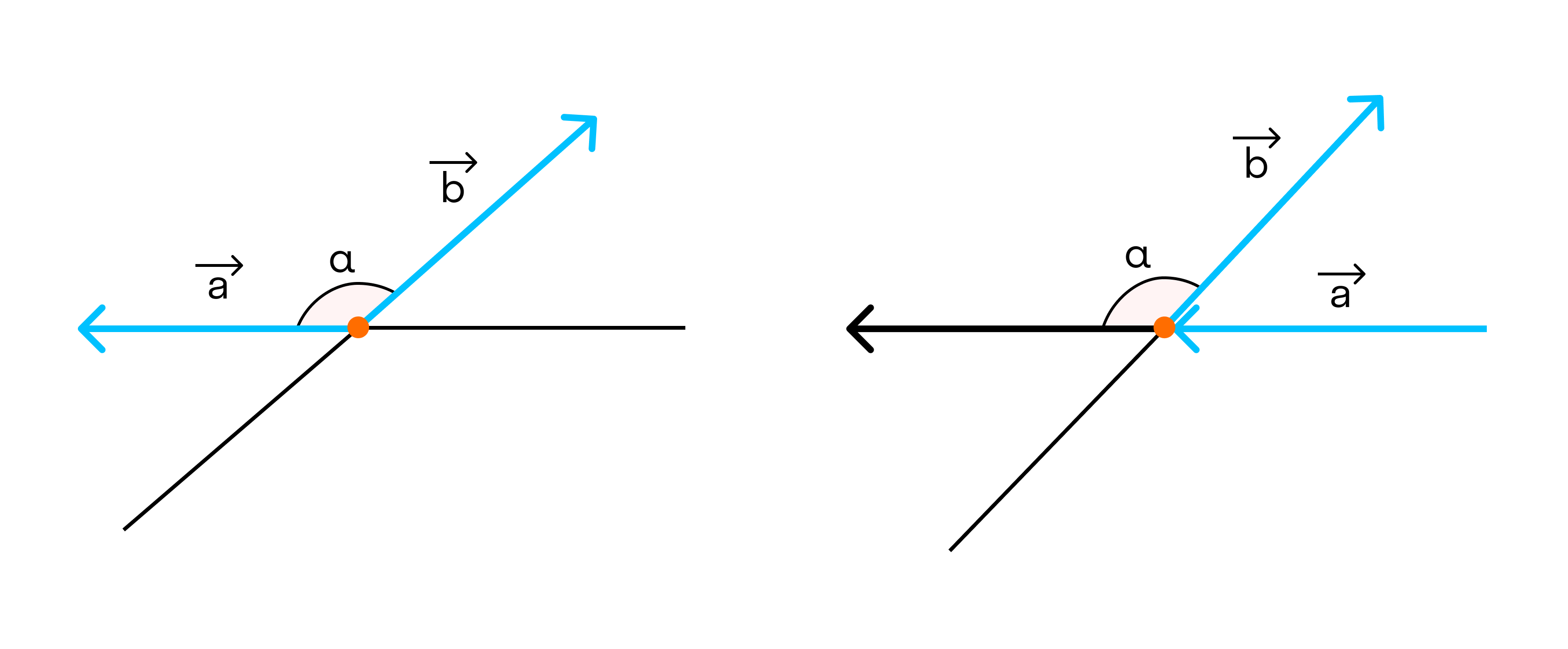
Угол между векторами ∠(→a, →b) может принимать значения от 0° до 180° градусов включительно. Аналитически это можно записать в виде двойного неравенства: 0°=

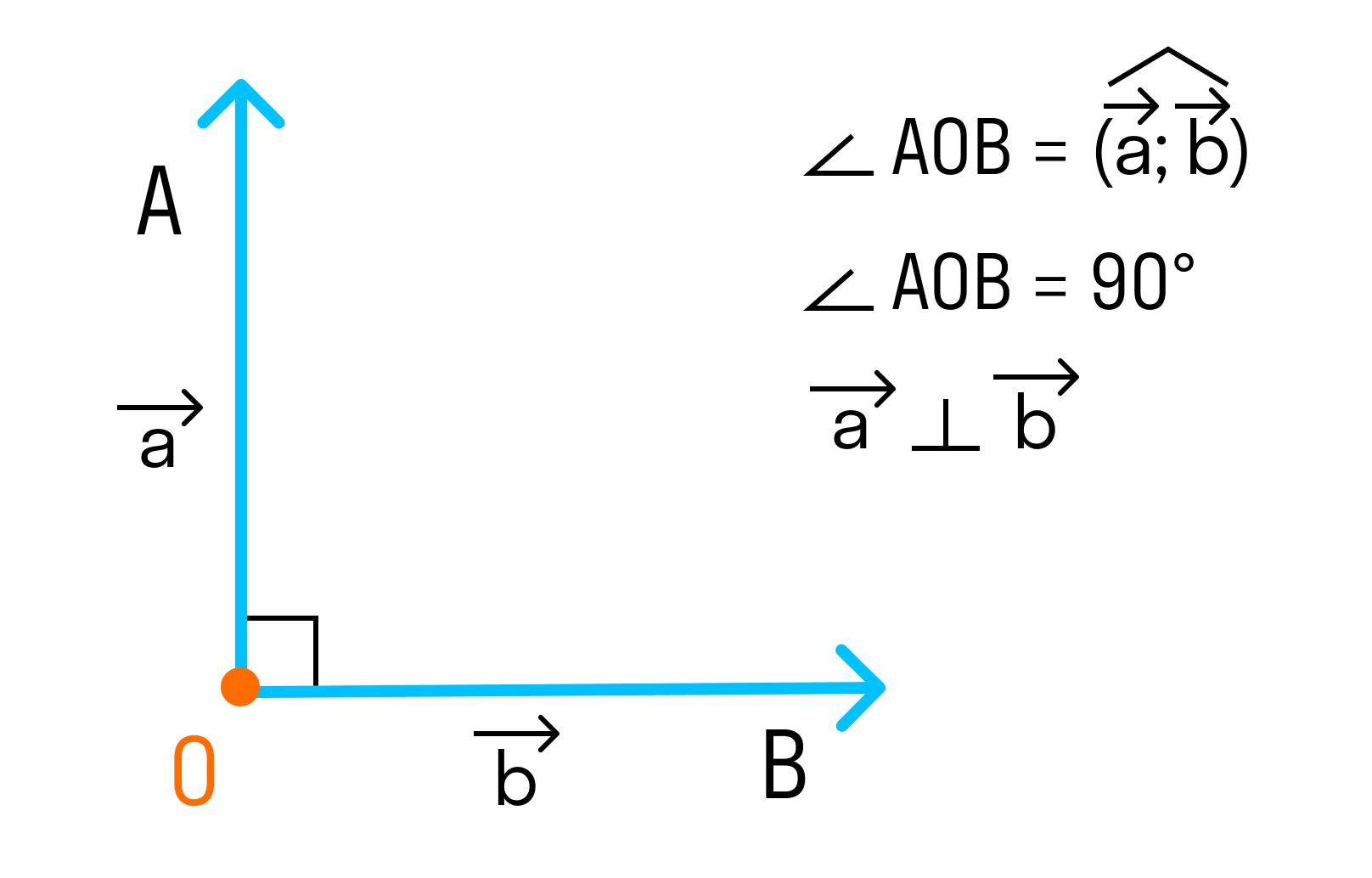
2. Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.

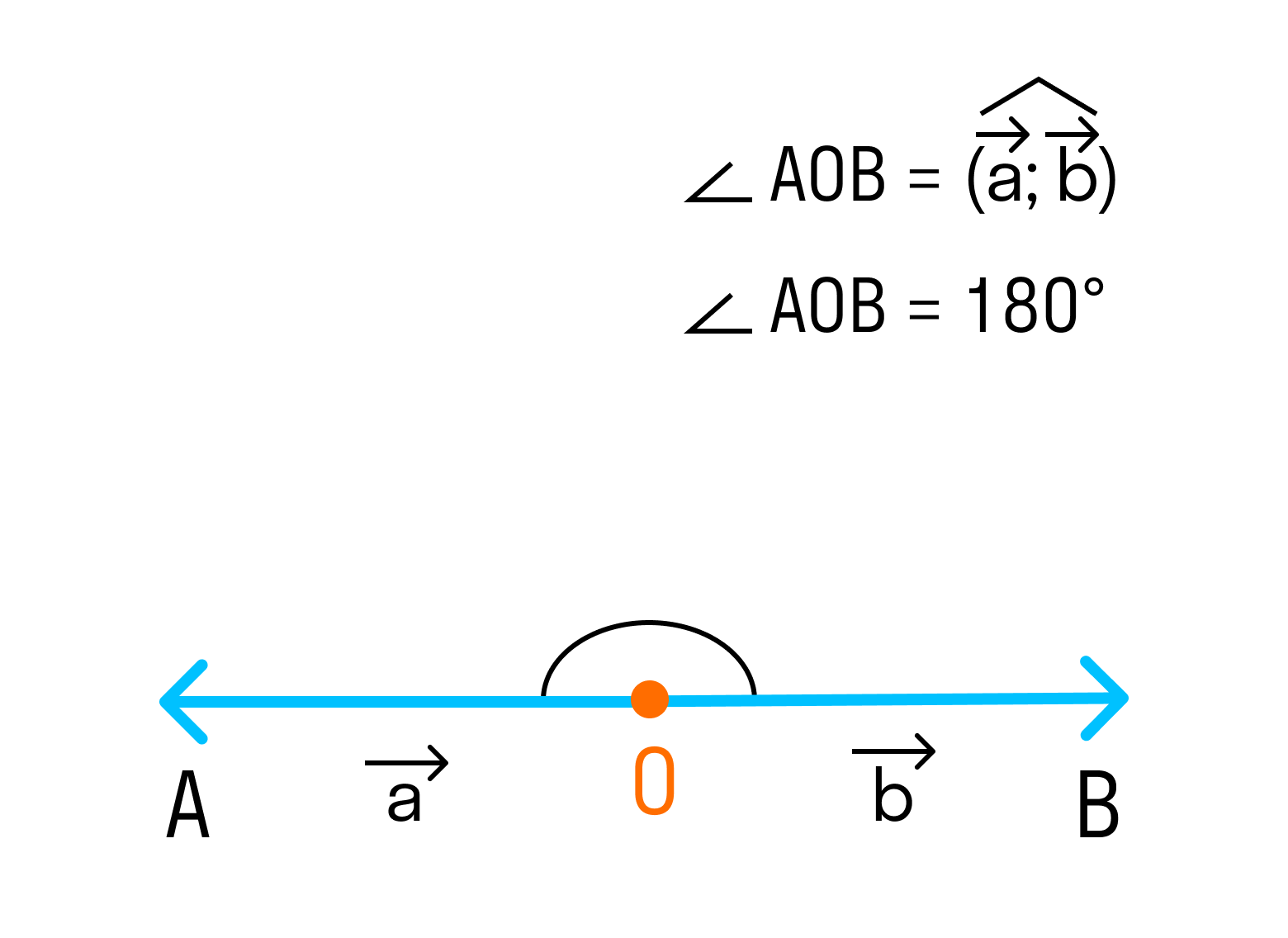
3. Если векторы направлены в разные стороны, тогда угол между ними 180°.

Также векторы могут образовывать тупой угол. Это выглядит так:

Скалярное произведение векторов

Определение скалярного произведения можно сформулировать двумя способами:

Скалярное произведение двух векторов a и b дает в результате скалярную величину, которая равна сумме попарного произведения координат векторов a и b.

Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:

Что важно запомнить про геометрическую интерпретацию скалярного произведения:

Скалярное произведение в координатах

Вычисление скалярного произведения можно произвести через координаты векторов в заданной плоскости или в пространстве.

Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов →a и →b.

То есть для векторов →a = (ax, ay), →b = (bx, by) на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид: (→a, →b) = ax*bx + ay*by

А для векторов →a = (ax, ay, az), →b = (bx, by, bz) в трехмерном пространстве скалярное произведение в координатах находится так: (→a, →b) = ax*bx + ay*by + az*bz

Докажем это определение:

для векторов →a = (ax, ay), →b = (bx, by) на плоскости, заданных в прямоугольной декартовой системе координат.

Отложим от начала координат (точка О) векторы →OB = →b = (bx, by) и →OA = →a = (ax, ay)

то последнее равенство можно переписать так:

а по первому определению скалярного произведения имеем

Записывайтесь на наши курсы по математике для учеников с 1 по 11 классы!

Формулы скалярного произведения векторов заданных координатами

Формула скалярного произведения векторов для плоских задач

В плоской задаче скалярное произведение векторов a = и b = можно найти по формуле:

a * b = ax * bx + ay * by

Формула скалярного произведения векторов для пространственных задач

В пространственной задаче скалярное произведение векторов a = и b = можно найти по формуле:

a * b = ax * bx + ay * by + az * bz

Формула скалярного произведения n-мерных векторов

Свойства скалярного произведения

Свойства скалярного произведения векторов:

a ≠ 0, b ≠ 0, a * b = 0 a ┴ b

Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.

Для примера докажем свойство коммутативности скалярного произведения (→a, →b) = (→b, →a)

По определению (→a, →b) = ax*bx + ay*by и (→b, →a) = bx*ax + by*ay. В силу свойства коммутативности операции умножения действительных чисел, справедливо ax*bx = bx*ax b ay*by = by*ay, тогда ax*bx + ay*by = bx*ax + by*ay.

Следовательно, (→a, →b) = (→b, →a), что и требовалось доказать.

Аналогично доказываются остальные свойства скалярного произведения.

Следует отметить, что свойство дистрибутивности скалярного произведения справедливо для любого числа слагаемых, то есть,

Примеры вычислений скалярного произведения

Пример 1.

Вычислите скалярное произведение двух векторов →a и →b, если их длины равны 3 и 7 единиц соответственно, а угол между ними равен 60 градусам.

У нас есть все данные, чтобы вычислить скалярное произведение по определению:

(→a,→b) = →|a| * →|b| * cos(→a,→b) = 3 * 7 cos60° = 3 * 7 * 1/2 = 21/2 = 10,5.

Ответ: (→a,→b) = 21/2 = 10,5.

Пример 2.

Найти скалярное произведение векторов →a и →b, если →|a| = 2, →|b| = 5, ∠(→a,→b) = π/6.

Используем формулу →a * →b = →|a| * →|b| * cosα.

→a * →b = →|a| * →|b| * cosα = 2 * 5 * cosπ/6 = 10 * √3/2 = 5√3

Пример 3.

Как найти скалярное произведение векторов →a = 7*→m + 3*→n и →b = 5*→m + 8*→n, если векторы →m и →n перпендикулярны и их длины равны 3 и 2 единицы соответственно.

По свойству дистрибутивности скалярного произведения имеем

Сочетательное свойство позволяет нам вынести коэффициенты за знак скалярного произведения:

В силу свойства коммутативности последнее выражение примет вид

Итак, после применения свойств скалярного произведения имеем

Осталось применить формулу для вычисления скалярного произведения через длины векторов и косинус угла между ними:

Пример 4.

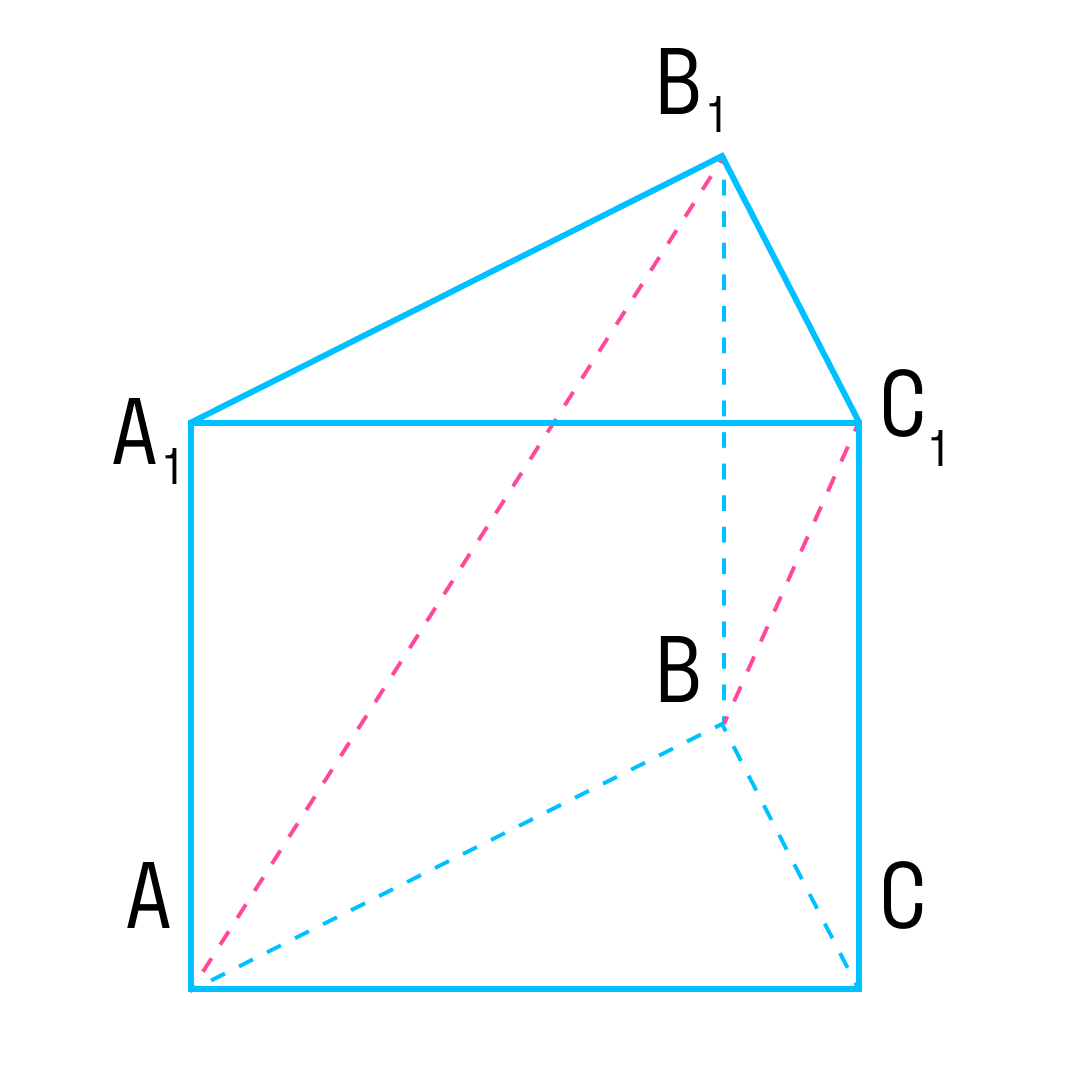
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найти косинус угла между прямыми AB1 и BC1.

Если сделать выносной рисунок основания призмы, получим понятный плоскостной рисунок с помощью которого можно легко найти координаты всех интересующих точек.

Пример 5.

б) Выяснить, будут ли перпендикулярными отрезки KL и MN, если K(3;5), L(-2;0), M(8;-1), N(1;4).

а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение: →ab = 1*6 + 2*(-1) + (-4)*1 = 0, следовательно

Обратите внимание на два существенных момента:

Ответ: а) →a перпендикулярно →b, б) отрезки KL, MN не перпендикулярны.

Пример 6.

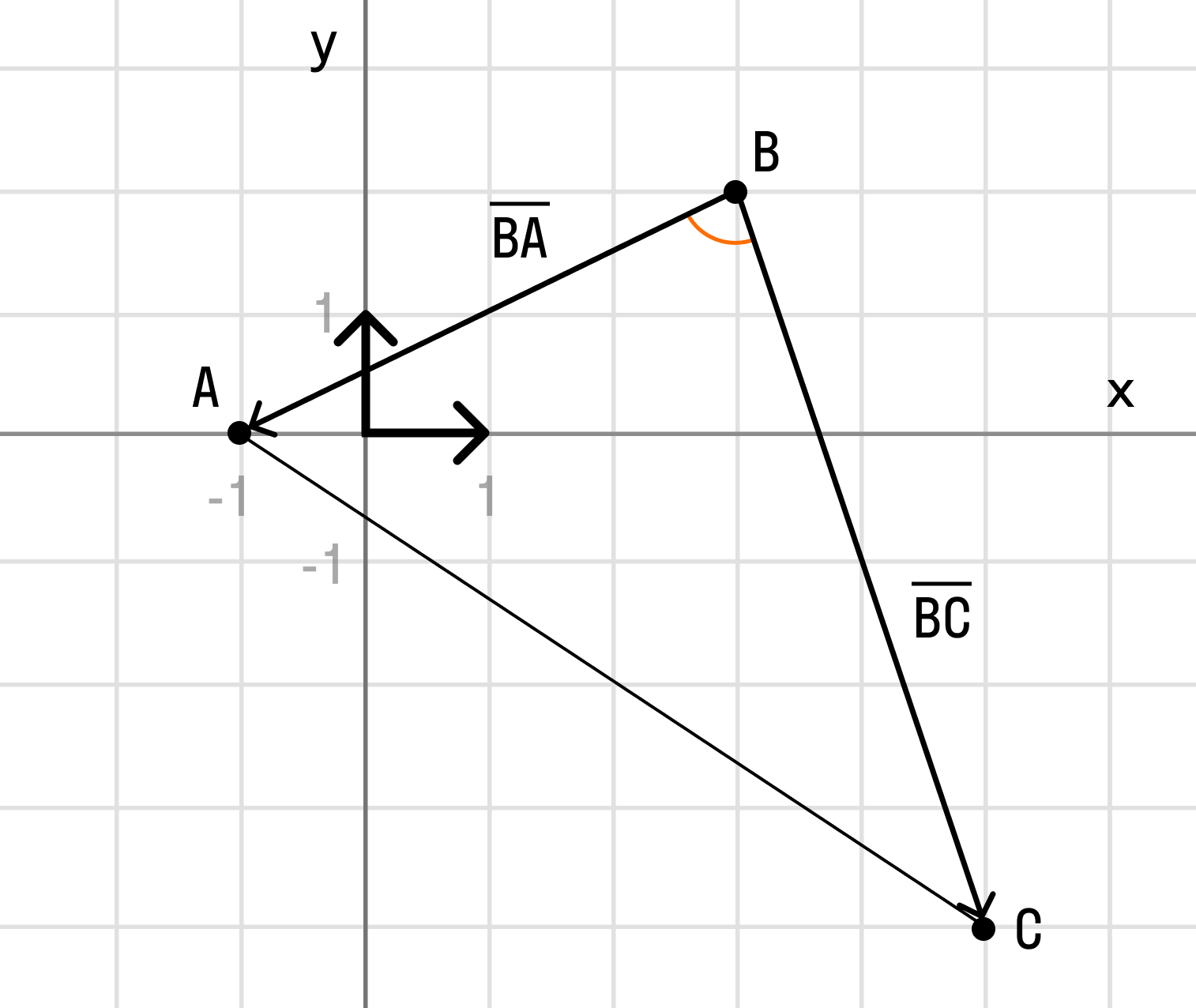
По условию чертеж выполнять не требуется, но для удобства можно сделать:

Требуемый угол ∠ABC помечен зеленой дугой. Сразу вспоминаем школьное обозначение угла: ∠ABC — особое внимание на среднюю букву B — это и есть нужная нам вершина угла. Для краткости можно также записать просто ∠B.

Из чертежа видно, что угол ∠ABC треугольника совпадает с углом между векторами →BA и →BC, иными словами: ∠ABC = ∠(→BA; →BC).

Вычислим скалярное произведение:

Вычислим длины векторов:

Найдем косинус угла:

Когда такие примеры не будут вызывать трудностей, можно начать записывать вычисления в одну строчку:

Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.

Если посмотреть на чертеж, то результат действительно похож на правду. Для проверки угол также можно измерить и транспортиром.

Ответ: ∠ABC = arccos(1/5√2) ≈1,43 рад. ≈ 82°

Важно не перепутать, что в задаче спрашивалось про угол треугольника, а не про угол между векторами. Поэтому указываем точный ответ: arccos(1/5√2) и приближенное значение угла: ≈1,43 рад. ≈ 82°, которое легко найти с помощью калькулятора.

А те, кому мало и хочется еще порешать, могут вычислить углы ∠A, ∠C, и убедиться в справедливости канонического равенства ∠A + ∠B + ∠C = 180°.

Источник

Что такое скаляр в математике

В физике существуют скалярные величины (скаляры) и векторные величины (векторы). Хотя, правильнее в последнем случае все-таки говорить векторная величина, часто говорят, например, «вектор скорости».

Чтобы совсем запутаться, рекомендую обратиться к Википедии: https://ru.wikipedia.org/wiki/Векторная_величина.

Для нас важно понять два момента:

1) Примерами скаляров являются: длина, площадь, время, масса, плотность, температура и т.п.

Для наших задач достаточно понимания скаляра, как величины (числа с размерностью) без направления.

2) Под вектором мы будем понимать направленный отрезок. То есть три числа (мы ведь живем в трехмерном пространстве), которые преобразуются по определенным правилам при переходе от одной системы координат к другой.

Попробуем обойтись без математических формул этих правил. Просто представим в нашем трехмерном пространстве направленный отрезок. Некую стрелку, которая, для простоты, неподвижна, неизменна, и имеет направление от одного конца к другому. Или даже представим, что у нас есть определенная операция перемещения в пространстве. У нее есть величина (расстояние перемещения по прямой из начальной точки в конечную) и направление.

И представим систему координат (например, прямоугольную), которая неподвижна относительно нас, и начало отсчета которой совпадает с началом нашего направленного отрезка.

Отлично! Тогда координаты «заостренного» конца нашего «направленного» отрезка с началом в точке (0,0,0) в этой системе координат будут выражаться тремя числами (А_х, А_y, А_z). Будет ли эта тройка чисел вектором?

Теперь мы берем и поворачиваем произвольно нашу систему координат (но пока не сдвигаем начало координат). Тогда в новой системе координат координаты нашего вектора будут (А_x’, А_y’, А_z’). Заметьте, сам наш вектор (направленный отрезок в трехмерном пространстве) не изменился. Как бы мы не вращали систему координат, тройка чисел будет меняться, но вектор (в смысле направленного отрезка) останется на своем месте. Он смотрит в одну и ту же «точку вселенной». О как! И длина его не меняется из-за вращения системы координат.

А теперь вывод. То, что важно для физики!

Формулы можно посмотреть у Фейнмана или еще где-нибудь. Они пока для понимания не столь важны. А важно следующее!

Теперь посмотрим, что есть что.

Путь вектор или скаляр? Скаляр. Почему?

Далее сами перебираем физические величины и определяем, что есть скаляр, а что вектор!

Источник