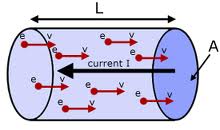
Что такое скорость дрейфа

Дрейф электронов под действием внешнего поля

При приложении к проводнику электрического поля Е в нем возникает электрический ток, плотность которого согласно закону Ома пропорциональна E:

(5.1)

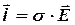
ρ =1/σ (5.2)

Возникновение тока в проводнике свидетельствует о том, что под действием поля электроны приобретают направленное движение, и функция распределения их по состояниям изменяется. Такое направленное движение называют дрейфом электронов, а среднюю скорость этого движения — скоростью дрейфа v_Д. Вычислим ее.

, (5.3)

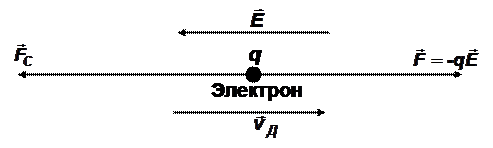
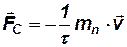
m_n — эффективная масса электрона.

Используя (5.3), уравнение направленного движения электрона в решетке можно записать в следующем виде:

(5.3′)

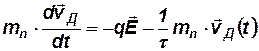
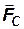
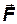
Из (5.3′) видно, что после включения поля скорость направленного движения электронов будет возрастать и они будут двигаться ускоренно до тех пор, пока сила сопротивления , пропорциональная скорости v_Д(t), не окажется равной силе , действующей со стороны поля. Когда эти силы сравняются, результирующая сила, действующая на электрон, и ускорение его движения будут равны нулю.

Начиная с этого момента, направленное движение электронов будет совершаться с постоянной скоростью

(5.4)

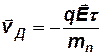
Так как заряд электрона отрицателен, то дрейф происходит в направлении, противоположном .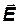

Отношение скорости дрейфа к напряженности поля называют подвижностью носителей:

(5.5)

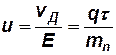
Подобная картина имела бы место при движении свободных электронов сквозь идеально правильную решетку со строго периодическим потенциалом. Электронная волна, описывающая поведение электрона в такой решетке, распространялась бы в ней практически без ослабле­ния, подобно световой волне, распространяющейся в оптически про­зрачной среде.

Причиной появления конечного электрического сопротивления являются всевозможные нарушения решетки, вызывающие искажения периодичности ее потенциала, на которых происходит рассеяние элек­тронных волн и ослабление направленного потока электронов подоб­но рассеянию световых волн и ослаблению светового пучка при про­хождении его через мутную среду.

Источник

Когда к проводнику приложена разность потенциалов, свободные электроны между последовательными столкновениями приобретают скорость в направлении, противоположном электрическому полю (и теряют скорость при движении в направлении поля), таким образом приобретая компонент скорости в этом направлении в дополнение к его случайная тепловая скорость. В результате возникает определенная малая дрейфовая скорость электронов, которая накладывается на беспорядочное движение свободных электронов. Из-за этой скорости дрейфа возникает чистый поток электронов, противоположный направлению поля.

СОДЕРЖАНИЕ

Экспериментальная мера

Формула для оценки скорости дрейфа носителей заряда в материале постоянной площади поперечного сечения имеет вид:

Это также можно записать как:

Но плотность тока и скорость дрейфа j и u на самом деле являются векторами, поэтому это соотношение часто записывается как:

Числовой пример

ты знак равно А электрон м 3 ⋅ м 2 ⋅ C электрон знак равно C s 1 м ⋅ C знак равно м s <\ displaystyle u = <\ dfrac <\ text > <<\ dfrac <\ text > <<\ text > ^ <3>>> <\ cdot> <\ text > ^ <2>\ cdot <\ dfrac <\ text > <\ text >>>> = <\ dfrac <\ dfrac <\ text > <\ text >> < <\ dfrac <1><\ text >> <\ cdot><\ text >>> = <\ dfrac <\ text > <\ text >>>

Источник

Скорость дрейфа

Когда к проводнику приложена разность потенциалов, свободные электроны между последовательными столкновениями приобретают скорость в направлении, противоположном электрическому полю (и теряют скорость при движении в направлении поля), таким образом приобретая компонент скорости в этом направлении в дополнение к его случайная тепловая скорость. В результате возникает определенная малая скорость дрейфа электронов, которая накладывается на беспорядочное движение свободных электронов. Из-за этой скорости дрейфа возникает чистый поток электронов, противоположный направлению поля.

СОДЕРЖАНИЕ

Экспериментальная мера [ править ]

Формула для оценки скорости дрейфа носителей заряда в материале с постоянной площадью поперечного сечения имеет следующий вид: [1]

Это также можно записать как:

Но плотность тока и скорость дрейфа j и u на самом деле являются векторами, поэтому это соотношение часто записывается как:

Числовой пример [ править ]

ты знак равно А электрон м 3 ⋅ м 2 ⋅ C электрон знак равно C s 1 м ⋅ C знак равно м s <\displaystyle u=<\dfrac <\text><<\dfrac <\text><<\text>^<3>>><\cdot ><\text>^<2>\cdot <\dfrac <\text><\text>>>>=<\dfrac <\dfrac <\text><\text>><<\dfrac <1><\text>><\cdot ><\text>>>=<\dfrac <\text><\text>>>

Источник

Микроскопический вид: скорость дрейфа

Физика > Микроскопический вид: скорость дрейфа

Рассмотрите скорость дрейфа электронов: роль проводников и электрического поля в движении зарядов, формула тока и дрейфа, скорость электрических сигналов.

Скорость дрейфа – средняя скорость, достигаемая частичкой из-за электрического поля.

Задача обучения

Основные пункты

Термин

Скорость дрейфа

Электрические сигналы перемещаются на больших скоростях. Достаточно хотя бы взглянуть на телефонные разговоры, транспортируемые токами в проводах и покрывающие огромные дистанции. Свет срабатывает, как только активируется переключатель.

Откуда такая высокая скорость у электрических сигналов? Дело в том, что сила между ними действует быстро на дистанции. Поэтому, когда свободный заряд вставляется в провод, входящий подталкивает к нему другие, которые и дальше нажимают на линии. В итоге, формируется электрическая ударная волна, проходящая сквозь систему практически со световой скоростью.

Когда заряженные частички вставляются в объем проводника, то равное число должно быстро удалиться. Отталкивание между подобными зарядами препятствует увеличению количества зарядов в объеме. Так что, по мере поступления одного заряда, второй убегает практически сразу, транспортируя сигнал вперед

Скорость дрейфа

Хорошие проводники обладает большим запасом свободных зарядов. В металлах – свободные электроны. Отдельный электрон между столкновением с атомами и прочими электронами перемещается на крошечную дистанцию, поэтому их пути оказываются практически случайными. Но проводники наделены электрическим полем, заставляющим электроны дрейфовать в конкретном направлении.

Скорость дрейфа электронов (v_d) – средняя скорость свободных зарядов после воздействия поля. Она довольно небольшая, потому что присутствует много свободных зарядов. Если располагать плотностью свободных электронов в проводнике, то можно высчитать скорость дрейфа. Чем выше плотность, тем ниже скорость.

Свободные электроны часто сталкиваются. Здесь вы видите путь конкретной частички. Скорость дрейфа расположена в противоположном направлении электрическому полю для электронов. Коллизии обычно транспортируют энергию на проводник, нуждаясь в стабильном поступлении энергии для поддержания постоянного тока

Интересно, что x/Δt – величина скорости дрейфа v_d, потому что заряды проходят среднюю дистанцию x за время t. Остальные показатели дают I = qnAv_d.

Плотность тока – электрический ток на единицу площади поперечного сечения.

Источник

Когда к проводнику приложена разность потенциалов, свободные электроны между последовательными столкновениями приобретают скорость в направлении, противоположном электрическому полю (и теряют скорость при движении в направлении поля), таким образом приобретая компонент скорости в этом направлении в дополнение к его случайная тепловая скорость. В результате возникает определенная малая дрейфовая скорость электронов, которая накладывается на беспорядочное движение свободных электронов. Из-за этой скорости дрейфа возникает чистый поток электронов, противоположный направлению поля.

СОДЕРЖАНИЕ

Экспериментальная мера

Формула для оценки скорости дрейфа носителей заряда в материале постоянной площади поперечного сечения имеет вид:

Это также можно записать как:

Но плотность тока и скорость дрейфа j и u на самом деле являются векторами, поэтому это соотношение часто записывается как:

Числовой пример

ты знак равно А электрон м 3 ⋅ м 2 ⋅ C электрон знак равно C s 1 м ⋅ C знак равно м s <\ displaystyle u = <\ dfrac <\ text > <<\ dfrac <\ text > <<\ text > ^ <3>>> <\ cdot> <\ text > ^ <2>\ cdot <\ dfrac <\ text > <\ text >>>> = <\ dfrac <\ dfrac <\ text > <\ text >> < <\ dfrac <1><\ text >> <\ cdot><\ text >>> = <\ dfrac <\ text > <\ text >>>

Источник