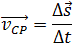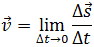Что такое скорость механика

Скорость

Ско́рость (часто обозначается , от англ. velocity или фр. vitesse ) — векторная физическая величина, характеризующая быстроту перемещения и направления движения материальной точки в пространстве относительно выбранной системы отсчёта (например, угловая скорость). Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.

В науке используется также скорость в широком смысле, как быстрота изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще изменения во времени, но также в пространстве или любой другой). Так, например, говорят о скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения, угловой скорости и т. д. Математически характеризуется производной функции.

Содержание

Скорость тела в механике

Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора этой точки:

Здесь — модуль скорости, — направленный вдоль скорости единичный вектор касательной к траектории в точке .

Скорость направлена вдоль касательной к траектории и равна по модулю производной дуговой координаты по времени.

Говорят, что тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).

В общем случае, скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса величина скорости точек на ободе относительно дороги принимает значения от нуля (в точке касания с дорогой) до удвоенного значения скорости автомобиля (в точке, диаметрально противоположной точке касания). Распределение скоростей в твёрдом теле определяется с помощью кинематической формулы Эйлера.

Если скорость тела (как векторная величина) не меняется во времени, то движение тела — равномерное (ускорение равно нулю) и тогда:

Скорость — характеристика движения точки, при равномерном движении численно равная отношению пройденного пути s к промежутку времени t, за который этот путь пройден.

Следует различать координатную и физическую скорости. При введении криволинейных или обобщённых координат положение тел описывается их зависимостью от времени. Производные от координат тела по времени при этом называются координатными скоростями.

Мгновенная и средняя скорость

Следует отличать понятие средней скорости перемещения от понятия средней скорости пути, равной отношению пройденного точкой пути ко времени, за которое этот путь был пройден. В отличие от скорости перемещения, средняя скорость пути — скаляр.

Когда говорят о средней скорости, для различения, скорость согласно выше приведённому определению называют мгновенной скоростью.

Так, хотя мгновенная скорость бегуна, кружащего по стадиону, в каждый момент времени отлична от нуля, его средняя скорость (перемещения) от старта до финиша оказывается равной нулю, если точки старта и финиша совпадают. Заметим, что при этом, средняя путевая скорость остаётся отличной от нуля.

В полярных координатах

Проекции скорости в декартовой системе координат

В то же время , поэтому

Таким образом, координаты вектора скорости — это скорости изменения соответствующей координаты материальной точки:

.

Преобразование скорости

В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S была равна , а скорость системы отсчёта S’ относительно системы отсчёта S равна , то скорость тела при переходе в систему отсчёта S’ будет равна .

Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы. При переходе из системы S в систему S’ необходимо использовать преобразования Лоренца для скоростей:

в предположении, что скорость направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.

Единицы измерения скорости

Соотношения между единицами скорости

См. также

Скорости волн
Групповая скорость | Фазовая скорость | Фронтовая скорость | Сигнальная скорость

Полезное

Смотреть что такое «Скорость» в других словарях:

СКОРОСТЬ — СКОРОСТЬ, скорости, мн. и, скоростей, жен. 1. только ед. (мн. спец.). Та или иная степень быстроты движения. Поезд двигался с большой скоростью. Автомобиль развил бешеную скорость. Эксплоатационная скорость поезда. Поставить рекорд скорости.… … Толковый словарь Ушакова

СКОРОСТЬ — в механике, одна из осн. кинематич. характеристик движения точки; величина векторная, определяемая равенством: v=dr/dt, где r радиус вектор точки, t время. При равномерном движении С. точки численно равна отношению пройденного пути s к промежутку … Физическая энциклопедия

СКОРОСТЬ — СКОРОСТЬ, характеристика поступательного движения точки (тела), численно равная при равномерном движении отношению пройденного пути s к промежуточному времени t, то есть v= s/t. При вращательном движении тела пользуются понятием угловой скорости … Современная энциклопедия

Скорость — СКОРОСТЬ, характеристика поступательного движения точки (тела), численно равная при равномерном движении отношению пройденного пути s к промежуточному времени t, то есть v= s/t. При вращательном движении тела пользуются понятием угловой скорости … Иллюстрированный энциклопедический словарь

СКОРОСТЬ — СКОРОСТЬ, и, мн. и, ей, жен. 1. Степень быстроты движения, распространения, действия. Развить с. Рекорд скорости бега. Двигаться на больших скоростях. С. звука (скорость распространения звуковых волн в среде). С. света (скорость распространения… … Толковый словарь Ожегова

скорость — скорость; мгновенная скорость Скорость точки жидкости, рассматриваемая как векторная функция переменных Эйлера … Политехнический терминологический толковый словарь

СКОРОСТЬ — СКОРОСТЬ, характеристика движения точки (тела), численно равная при равномерном движении отношению пройденного пути к промежутку времени, за которое этот путь пройден. Скорость (физическая) характеризует движение тела в определенном направлении,… … Научно-технический энциклопедический словарь

Скорость — Скорость, лазание на скорость вид скалолазания со следующими специфическими особенностями: большая протяженность большая высота, необходима страховка с веревкой на соревнованиях применяется верхняя страховка относительно несложные движения… … Энциклопедия туриста

Источник

Основы механики для чайников. Часть 1: Кинематика

В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.

Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.

Траектория, радиус-вектор, закон движения тела

Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.

Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.

Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.

Радиус-вектор – вектор, задающий положение точки в пространстве.

Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.

Перемещение и путь

Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.

В системе СИ перемещение и длина пути измеряются в метрах.

Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.

Скорость и ускорение

Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло

А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.

Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.

В системе СИ скорость измеряется в метрах в секунду

Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.

Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости

Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.

Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории

Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.

Здесь R – радиус окружности, по которой движется тело.

Закон равноускоренного движения

Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.

Производная по скорости от времени даст значение ускорения a, которое является константой.

Пример решения задачи

Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.

Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.

Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.

Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.

Источник

Скорость механического движения

Вы будете перенаправлены на Автор24

Механическое движение – это изменение расположения тела в пространстве касательно других точек.

Например, автомобиль движется по дороге и в нем находятся люди. Они осуществляют движение вместе с транспортом по трассе. То есть люди передвигаются в пространстве относительно дороги, но относительно самой машины люди не движутся.

Из этого примера видно, что, изначально необходимо определить тело, рассматриваемое в движении, которое в наук называют точкой отсчета. Система координат тесно взаимосвязана с методикой измерения времени, что в результате создают концепцию отсчета.

Понятие скорости механического движения

Скорость – физическая величина, которая равна перемещению тела к интервалу времени, в течение которого это взаимодействие произошло.

Механическое движение оценивается еще и тем, как быстро перемещается тело (точка). Это и есть скорость движения. Скорость представляет собой понятие векторной величины. Для того, чтобы в полном объеме задать ее, необходимо установить непосредственно направление и величину скорости, вдоль которых она была изначально замерена. Как правило скорость элементов рассматривают по траектории движения. В таком случае величина исследуемого объекта обусловливается как путь, пройденный за одну единицу времени. Другими словами, для нахождения правильного коэффициента траектории движения, путь тела надо разделить на время, в течение которого он был пройден.

Готовые работы на аналогичную тему

Мгновенная скорость – это скорость точки в конкретный момент времени или в определенной точке траектории.

Это векторная физическая величина, численно равная пределу, к которому устремляется средняя скорость за очень малый промежуток времени. Указанная траектория является первой производной от вектора в соответствии с временем. Вектор моментальной скорости определяется по касательной к линии движения тела в сторону его дальнейшего перемещения.

Эта величина дает точное представление о движении объекта в данный момент времени.

Например, во время поездки в автомобиле в определенный момент времени водитель смотрит на спидометр и видит, что на табло 100 км/ч. Затем стрелка указывает на 90 км/ч, а спустя пару минут – 110 км/ч.

Значением мгновенной скорости транспорта в определенные моменты времени являются полученные показания прибора.

Имеется ли физический смысл в понятии «мгновенной скорости»? Данный термин характеризуется изменением перемещения элементов в пространстве. Но, чтобы узнать, как изменилось его расположение, следует наблюдать за движением в течение определенного периода времени.

Даже самые современные приборы для замера скорости измеряют движение за конкретный отрезок времени – конечный временной интервал. Определение «скорость тела на данный момент» не считается корректным с точки зрения физики. Однако, именно этот тезис очень удобен в математических расчетах, поэтому им пользуются постоянно.

Закон сложения скоростей

Скорость любого физического тела относительно неподвижной концепции отсчета всегда равна векторной сумме перемещения элементов относительно подвижной системы. Эта теория помогает точно определить расположение объекта в конкретный период времени.

Необходимо понимать, что скорость является векторной величиной. По траектории движения возможно определить только направление скорости вектора. Вектор скорости направлен по касательной к траектории, по которой проходит тело, что движется на данный момент.

Отрицательная скорость

Скорость тела может быть отрицательной в случае, когда тело движется в противоположном направлении от оси координат в выбранной системе отсчета.

Ученый из Великобритании, Роберта Бойд смог присвоить пучку света «отрицательную» скорость, при которой пик импульса продвигался к источнику, а не от него. Интересно, если менять среду специальным образом и пропускать через нее через свет, возможно легко управлять скоростью светового импульса — «замораживая» или замедлять его в десятки тысяч раз, а то и вовсе останавливать.

В этом аспекте речь идет о групповой скорости, которая определяет скорость распространения одного пучка импульса света. Из-за рассеивания этот элемент может передвигаться на несколько порядков медленнее, чем каждый фотон в отдельности, и наоборот —стремительнее скорости света в вакууме.

В данном случае речь не идет о нарушении законов природы, потому как самые первые фотоны в импульсе добегают до конца, не «быстрее света». В случае же остановки светового пучка необходимо говорить о поглощении импульса подготовленной средой с повторным излучением. При этом сохраняются все важные параметры исходного объекта, «до последнего фотона».

Источник

Скорость

Скорость – это количественная характеристика движения тела.

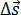
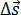
Средняя скорость – это физическая величина, равная отношению вектора перемещения точки к промежутку времени Δt, за который произошло это перемещение. Направление вектора средней скорости совпадает с направлением вектора перемещения Средняя скорость определяется по формуле:

Мгновенная скорость, то есть скорость в данный момент времени – это физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:

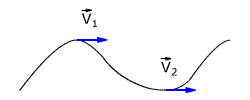
Иными словами, мгновенная скорость в данный момент времени – это отношение очень малого перемещения 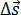к очень малому промежутку времени, за который это перемещение произошло.

Вектор мгновенной скорости направлен по касательной к траектории движения тела (рис. 1.6).

Рис. 1.6. Вектор мгновенной скорости.

В системе СИ скорость измеряется в метрах в секунду, то есть единицей скорости принято считать скорость такого равномерного прямолинейного движения, при котором за одну секунду тело проходит путь в один метр. Единица измерения скорости обозначается м/с. Часто скорость измеряют в других единицах. Например, при измерении скорости автомобиля, поезда и т.п. обычно используется единица измерения километр в час:

Сложение скоростей

Скорости движения тела в различных системах отсчёта связывает между собой классический закон сложения скоростей.

Скорость тела относительно неподвижной системы отсчёта равна сумме скоростей тела в подвижной системе отсчёта и самой подвижной системы отсчёта относительно неподвижной.

Например, пассажирский поезд движется по железной дороге со скоростью 60 км/ч. По вагону этого поезда идет человек со скоростью 5 км/ч. Если считать железную дорогу неподвижной и принять её за систему отсчёта, то скорость человека относительно системы отсчёта (то есть относительно железной дороги), будет равна сложению скоростей поезда и человека, то есть

Однако это справедливо только в том случае, если человек и поезд движутся по одной линии. Если же человек будет двигаться под углом, то придётся учитывать этот угол, вспомнив о том, что скорость – это векторная величина.

А теперь рассмотрим описанный выше пример более подробно – с деталями и картинками.

Итак, в нашем случае железная дорога – это неподвижная система отсчёта. Поезд, который движется по этой дороге – это подвижная система отсчёта. Вагон, по которому идёт человек, является частью поезда.

Свяжем с неподвижной системой отсчёта (рис. 1.7) систему координат ХОY, а с подвижной системой отсчёта – систему координат X_ПО_ПY_П (см. также раздел Система отсчёта). А теперь попробуем найти скорость человека относительно неподвижной системы отсчёта, то есть относительно железной дороги.

Это закон сложения перемещений. В нашем примере перемещение человека относительно железной дороги равно сумме перемещений человека относительно вагона и вагона относительно железной дороги.

Рис. 1.7. Закон сложения перемещений.

Это закон сложения скоростей:

Источник

Скорость в классической механике

Вы будете перенаправлены на Автор24

Классическая механика считается разновидностью механики (специального раздела), созданного учеными в целях исследования законов об изменениях положения объектов в пространстве с течением определенного времени, а также – причин, спровоцировавших данные процессы.

Рисунок 1. Преобразования Галилея. Автор24 — интернет-биржа студенческих работ

Поскольку классическая механика базируется на законах Ньютона и принципе относительности, разработанном Галилеем, у нее появилось второе название – «Ньютоновская механика». Одним из важных моментов при изучении классической механики является исследование скоростей.

Суть классической механики

Изучение скоростей в классической механике предусматривает предварительное рассмотрение самой сути данного раздела физики. С этой целью, она состоит из нескольких важных аспектов, представляющих огромный интерес для физиков:

Классическая механика может обеспечить максимально точные результаты в случае ограниченности ее применения телами, обладающими скоростями, намного уступающими по показателю скорости света.

Наряду с тем, классическая механика доказала свое огромное значение в плане скоростей объектов, благодаря своим уникальным свойствам:

Ее можно применять с целью описания движения объектов, подобных «волчку» и бейсбольному мячу. Она исключает существование противоречащих друг другу утверждений.

Стоит, однако, отметить, предупреждают физики, что объединение классической механики с некоторыми другими классическими теориями (классическая электродинамика или термодинамика) автоматически провоцирует возникновение неразрешимых противоречий. Классическая электродинамика предполагает постоянство скорости света для всех наблюдателей (здесь уже наблюдается несовместимость с принципами действия классической механики).

Готовые работы на аналогичную тему

Физические основы классической механики

Рисунок 2. Физические основы классической механики. Автор24 — интернет-биржа студенческих работ

Впервые принципы механики сформулировал И. Ньютон, что произошло в 1687 году в рамках экспериментальных исследований перемещений макротел с незначительными (сравнительно со скоростью света) скоростями в условиях вакуумного пространства.

В основу классической механики положены следующие главные представления Ньютона относительно свойств времени и пространства:

Релятивистская механика предусматривает наблюдение за движением макротел с близкими к скорости света в вакууме скоростями.

Квантовая механика изучает микрочастицы, чье движение характеризуется скоростью, существенно меньшей, чем скорость света в вакуумном пространстве.

С целью определения принадлежности микрочастицы к макроскопическим и вероятности применения в отношении нее классических формул, имеет смысл задействовать принцип неопределенности Гейзенберга, при котором реальные частицы можно охарактеризовать посредством импульса и координаты лишь с незначительной неточностью.

Физики отмечают, что в действительности, движения тел оказываются настолько сложными, что при их изучении имеет смысл отвлечься от несущественных для исследуемого движения деталей (иначе задача осложнилась бы настолько, что ее решение стало бы практически невозможным).

В этом плане задействованы такие понятия, как идеализация и абстракция, чье использование взаимозависимо от конкретного характера интересующих нас задач и от показателя точности, с которой мы желаем получить результат. Среди таких понятий существенная роль отводится материальной точке, абсолютно твердому телу и системе материальных точек.

Материальная точка представляет собой физическое понятие с целью описания поступательного движения тела при условии низкого показателя его линейных размеров (если сравнивать с аналогичным показателем других тел) в пределах предварительно заданной точности вычисления координаты тела.

Физики отмечают отсутствие в природе материальных точек и предлагают рассматривать одно и то же тело (в зависимости от характера условий) либо в качестве материальной точки или тела с конечными размерами.

Так, движущаяся вокруг Солнца Земля может по праву считаться материальной точкой, но при этом, в случае исследования ее вращения вокруг своей оси, она уже таковой являться не будет. Это, в свою очередь, объясняется существенным влиянием формы и размеров Земли на характер подобного движения, а сам путь прохождения определенной точкой земной поверхности за временной период, равный времени ее обращения вокруг собственной оси, окажется равнозначным линейным размерам земного шара.

Самолет также можно рассматривать в качестве материальной точки в случае изучения движения его центра масс. В то же время, при необходимости учитывания воздействия среды либо определения усиления в отдельных его частях, его приходится рассматривать уже в качестве абсолютно твердого тела.

Закон сложения скоростей в классической механике

В рамках действия законов и принципов классической механики, абсолютная скорость точки равнозначна векторной сумме её переносной и относительной скоростей. Данное равенство, в свою очередь, характеризуется утверждением теоремы сложения скоростей.

Иными словами, в более детальном выражении, она звучит так: скорость движения тел, относительно неподвижных систем отсчёта, будет равнозначна векторной сумме скорости указанного тела в отношении к подвижной системе скорости и отсчета, где в конкретный момент времени пребывает тело.

Таким образом, ученые предлагают следующие выводы, относительно действия законов скорости на простых примерах в классической механике:

Источник