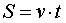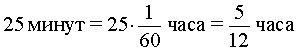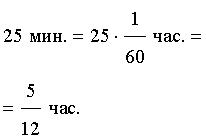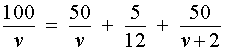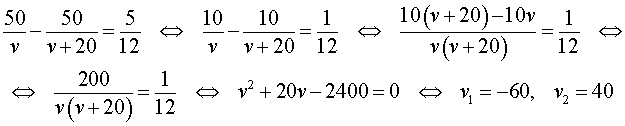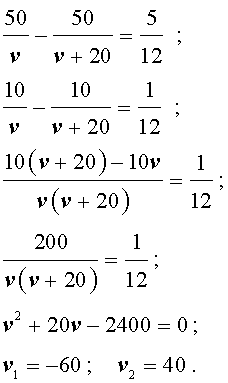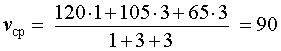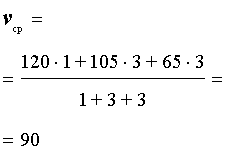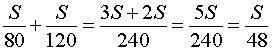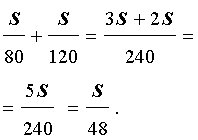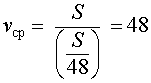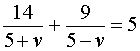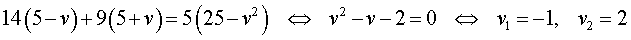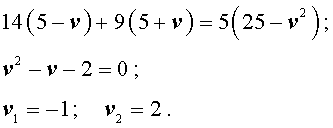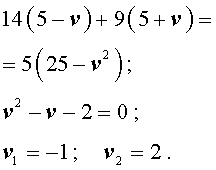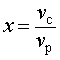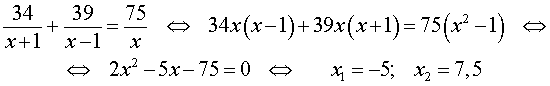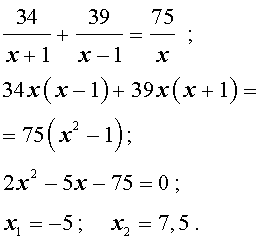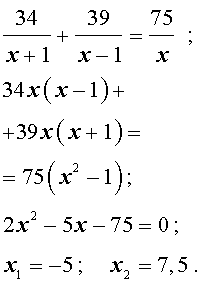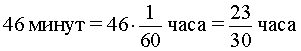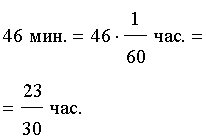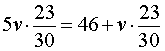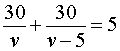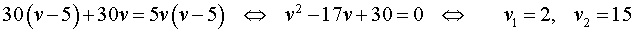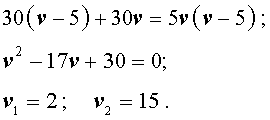Что такое скорость собственная скорость
Задачи на движение по воде
Разделы: Математика
Данный материал представляет собой систему задач по теме “Движение”.
Цель: помочь учащимся более полно овладеть технологиями решения задач по данной теме.
Задачи на движение по воде.
Очень часто человеку приходится совершать движения по воде: реке, озеру, морю.
Сначала он это делал сам, потом появились плоты, лодки, парусные корабли. С развитием техники пароходы, теплоходы, атомоходы пришли на помощь человеку. И всегда его интересовали длина пути и время, затраченное на его преодоление.
В озере они будут стоять на месте, а в реке – плыть.
Рассмотрим первый вариант: лужа и озеро. Вода в них не движется и называется стоячей.
Кораблик поплывет по луже только в том случае, если мы его подтолкнем или если подует ветер. А лодка начнет двигаться в озере при помощи весел или если она оснащена мотором, то есть за счет своей скорости. Такое движение называют движением в стоячей воде.
Отличается ли оно от движения по дороге? Ответ: нет. А это значит, что мы с вами знаем как действовать в этом случае.
Задача 1. Скорость катера по озеру равна 16 км/ч.
Какой путь пройдет катер за 3 часа?
Следует запомнить, что скорость катера в стоячей воде называют собственной скоростью.
Задача 2. Моторная лодка за 4 часа проплыла по озеру 60 км.
Найдите собственную скорость моторной лодки.
Задача 3. Сколько времени потребуется лодке, собственная скорость которой
равна 28 км/ч, чтобы проплыть по озеру 84 км?
Итак, чтобы найти длину пройденного пути, необходимо скорость умножить на время.
Чтобы найти скорость, необходимо длину пути разделить на время.
Чтобы найти время, необходимо длину пути разделить на скорость.
Чем же отличается движение по озеру от движения по реке?
Вспомним бумажный кораблик в ручье. Он плыл, потому что вода в нем движется.
Такое движение называют движением по течению. А в обратную сторону – движением против течения.
Итак, вода в реке движется, а значит имеет свою скорость. И называют ее скоростью течения реки. ( Как ее измерить?)
Задача 4. Скорость течения реки равна 2 км/ч. На сколько километров река относит
любой предмет (щепку, плот, лодку) за 1час, за 4 часа?
Те же, кто не умеет плавать, могут представить себе ситуацию, когда дует сильный ветер. Рассмотрим два случая:
1) ветер дует в спину,
2) ветер дует в лицо.
И в том и в другом случае идти сложно. Ветер в спину заставляет бежать, а значит, скорость нашего движения увеличивается. Ветер в лицо сбивает нас, притормаживает. Скорость при этом уменьшается.
Остановимся на движении по течению реки. Мы уже говорили о бумажном кораблике в весеннем ручье. Вода понесет его вместе с собой. И лодка, спущенная на воду, поплывет со скоростью течения. Но если у нее есть собственная скорость, то она поплывет еще быстрее.
Следовательно, чтобы найти скорость движения по течению реки, необходимо сложить собственную скорость лодки и скорость течения.
Задача 5. Собственная скорость катера равна 21 км/ч, а скорость течения реки 4 км/ч. Найдите скорость катера по течению реки.
Теперь представим себе, что лодка должна плыть против течения реки. Без мотора или хотя бы весел, течение отнесет ее в обратную сторону. Но, если придать лодке собственную скорость ( завести мотор или посадить гребца), течение будет продолжать отталкивать ее назад и мешать двигаться вперед со своей скоростью.
Поэтому, чтобы найти скорость лодки против течения, необходимо из собственной скорости вычесть скорость течения.
Задача 6. Скорость течения реки равна 3 км/ч, а собственная скорость катера 17 км/ч.
Найдите скорость катера против течения.
Задача 7. Собственная скорость теплохода равна 47,2 км/ч, а скорость течения реки 4,7 км/ч. Найдите скорость теплохода по течению и против течения.
Ответ: 51,9 км/ч; 42,5 км/ч.
Задача 8. Скорость моторной лодки по течению равна12,4 км/ч. Найдите собственную скорость лодки, если скорость течения реки 2,8 км/ч.
Задача 9. Скорость катера против течения равна 10,6 км/ч. Найдите собственную скорость катера и скорость по течению, если скорость течения реки 2,7 км/ч.
Ответ: 13,3 км/ч; 16 км/ч.
Связь между скоростью по течению и скоростью против течения.
Введем следующие обозначения:
Тогда можно записать следующие формулы:
Попытаемся изобразить это графически:
Вывод: разность скоростей по течению и против течения равна удвоенной скорости течения.
Vno теч — Vnp. теч = 2 Vтеч.
1) Скорость катера против течения равна 23 км/ч, а скорость течения 4 км/ч.
Найдите скорость катера по течению.
2) Скорость моторной лодки по течению реки равна 14 км/ч/ а скорость течения 3 км/ч. Найдите скорость лодки против течения
Задача 10. Определите скорости и заполните таблицу:
Формула нахождения значений скорости, времени и расстояния
С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.
Как же рассчитать скорость?
На самом деле, рассчитать ее можно несколькими способами:
Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.
Теперь нужно подставить имеющиеся значения вместо буквенных символов:
v=100 км/1,5 ч=66,66 км/ч
Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.
Таким нехитрым способом можно найти скорость через время и расстояние.
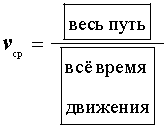
А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
Можно записать использовать и такой вид вычислений:
Но можно записать эту же формулу и в более точном варианте:
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.
Другие способы вычисления
Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:
Способы вычисления расстояния и времени
Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:
Таким образом вычисляется значение расстояния.
Или вычисляем значение времени, за которое пройдено расстояние:
Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.
Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.
И это еще не предел!
Видео
В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.
Что такое скорость собственная скорость
Пн-Пт 9:00-19:00
Сб-Вс 10:00-16:00
Как рассчитать по формулам скорость лодки?
Собрали для Вас актуальные формулы, которые могут оказаться полезными каждому 
✓ Формула 1
На примере разберем, как находить скорость лодки.
Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.
Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. — Vпр. теч)/2, найдем:
Vтеч = (21,8 — 17,2)/2=4,6\2=2,3 (км/ч)
Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)
Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).
✓ Формула 2
Самым простым методом самостоятельного расчета предельной скорости лодки считается использование формулы, учитывающей параметры двигателя.
Для этого используется формула вычисления двигателя V = NK/R, где искомый параметр V – скорость километров в час, R – сопротивление движению (его вы можете взять в технической документации своего катера), K – коэффициент полезной деятельности винта. Определяется он в зависимости от типа лодки. Так, для спортивного катера его значение — 160, для крупных винтов — 140, для средних и малых — 120 и 100 соответственно.
Параметр N – мощность работы двигателя катера. Эту информацию вы можете рассчитать самостоятельно или обратиться за помощью к технической документации. Для того, чтобы вычислить предел скорости катера, возьмите максимально допустимую мощность. Этот метод позволяет рассчитать предел максимальной скорости катера достаточно точно, однако не следует забывать про вероятную погрешность.
Возможно вам будет интересным
История производства подвесных лодочных моторов
С чего все началось? Рассказываем!
15 сентября 2020 432
Что такое виндсерфинг и зачем он нужен?
Подробнее рассказываем в нашей статье!
31 августа 2020 352
Этапы получения прав на маломерное судно
Получение любых прав на средства передвижения требуют определенных затрат, например: сбор необходимых документов, обучение, экзамены и многое другое. Рассказываем подробнее.
27 августа 2020 449
В чем плюсы бронирования лодок ПВХ?
Рассказываем особенности, читайте
20 августа 2020 382
5 мифов про лодки ПВХ
Таинственные лодки ПВХ и какие мифы их окружают?
17 августа 2020 359
Почему покупают детские велосипеды?
Хотите порадовать ребенка велосипедом? Отлично, наш ассортимент полон детских велосипедов!
10 августа 2020 346
Что нужно знать перед покупкой велосипеда?
Какие бывают велосипеды? Как выбрать? Читайте в статье
Как выбрать лодочный мотор?
Отвечаем на Вопросы наших покупателей
Что такое килеватость судна и на что влияет?
Читайте подробнее в статье!
14 июля 2020 1 024
Пункт выдачи заказов:
г. Санкт-Петербург, ул. Софийская д. 8к1 БЦ Крол
Пн-Сб 10:00-19:00
Вс 10:00-18:00
Остались вопросы?
Задайте их нам прямо сейчас!
© Море Моторов, 2021 | Все права защищены
Предложения, размещенные на сайте more-motorov.ru, не являются публичной офертой
Пожалуйста, введите Ваши данные, и менеджер свяжется с Вами в ближайшее время
Задачи на движение
Скорость тела. Средняя скорость тела
Решение задач на движение опирается на хорошо известную из курса физики формулу
Сразу же сделаем важное
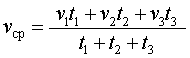 | (2) |
– время движения автобуса по расписанию (в часах);
– время, за которое автобус проехал первую половину пути (в часах);
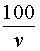
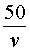
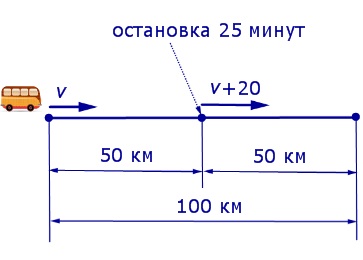
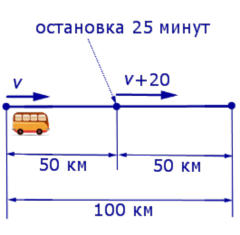
v + 20 – скорость автобуса во второй половине пути (в км/час);
– время, за которое автобус проехал вторую половину пути (в часах).
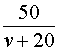
В условии задачи дано время остановки автобуса – 25 минут. Его необходимо выразить в часах, чтобы все единицы измерения были согласованными:
Теперь можно составить уравнение, исходя из того, что автобус прибыл в конечный пункт вовремя, а, значит, время, которое он был в пути, плюс время остановки должно равняться времени движения автобуса по расписанию:
Решим это уравнение:
По смыслу задачи первый корень должен быть отброшен.
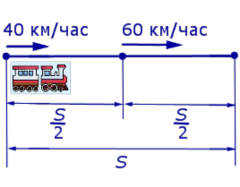
Задача 2. (МИОО) Первый час автомобиль ехал со скоростью 120 км/час, следующие три часа – со скоростью 105 км/час, а затем три часа – со скоростью 65 км/час. Найдите среднюю скорость автомобиля на протяжении всего пути.
– время, за которое поезд прошел первую половину пути, выраженное в часах;
– время, за которое поезд прошел вторую половину пути, выраженное в часах.
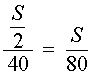
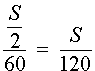
Следовательно, время, за которое поезд прошел весь путь, равно
В соответствии с формулой (1) средняя скорость поезда на протяжении всего пути
Движение по реке. Скорость течения реки
В отличие от задач на движение по суше, в задачах на движение по реке появляется новая величина – скорость течения реки.
По отношению к берегу, который неподвижен, скорость тела, движущегося по течению реки, равна сумме собственной скорости тела ( скорости тела по озеру, скорости тела в неподвижной воде, скорости тела в стоячей воде ) и скорости течения реки. По отношению к берегу скорость тела, движущегося против течения реки, равна разности собственной скорости тела и скорости течения реки.
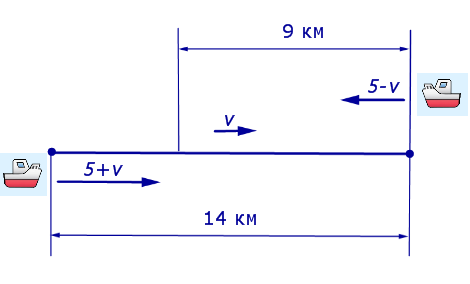
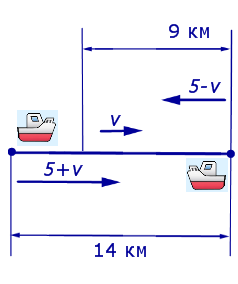
5 + v – скорость, с которой лодка шла по течению реки (в км/час);
– время движения лодки по течению реки (в часах);
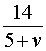
5 – v – скорость, с которой лодка шла против течения реки (в км/час);
– время движения лодки против течения реки (в часах);
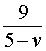
Теперь можно составить уравнение, принимая во внимание тот факт, что лодка находилась в пути 5 часов:
Решим это уравнение:
По смыслу задачи первый корень должен быть отброшен.
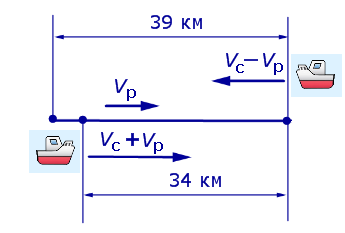
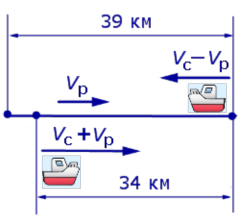
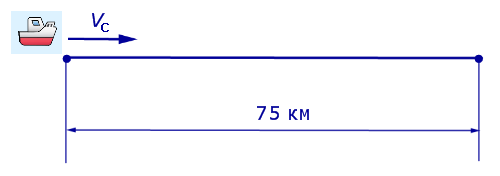
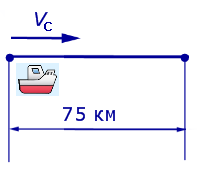
Задача 5. (Бюро «Квантум») Моторная лодка прошла по течению реки 34 км и 39 км против течения, затратив на это столько же времени, сколько ей нужно, чтобы пройти 75 километров в стоячей воде. Найдите отношение скорости лодки в стоячей воде к скорости течения реки.
Учитывая тот факт, что в обеих ситуациях лодка провела в пути одно и то же время, можно составить уравнение:
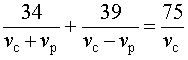 | (3) |
Если ввести обозначение
то, воспользовавшись формулой
перепишем уравнение (3) в виде
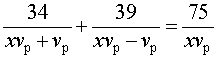 | (4) |
По смыслу задачи первый корень должен быть отброшен.
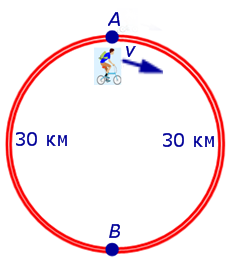
Движение по кольцевым трассам
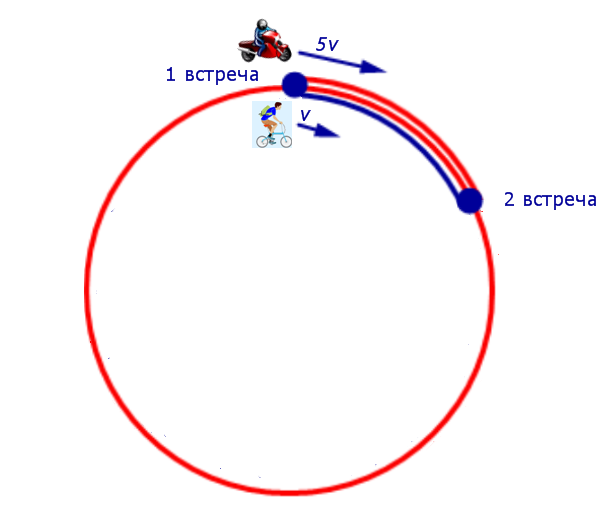
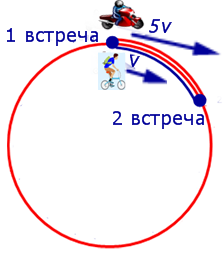
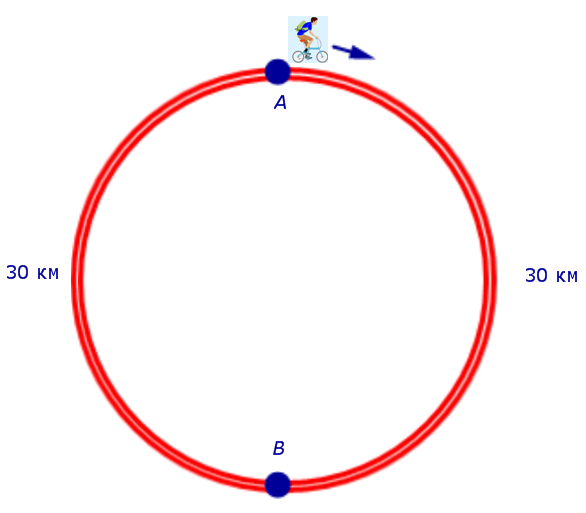
Задача 6. (www.reshuege.ru) Из пункта A круговой трассы длиной 46 км выехал велосипедист, а через 20 минут из пункта A следом за велосипедистом отправился мотоциклист. Через 5 минут после отправления мотоциклист догнал велосипедиста в первый раз, а еще через 46 минут после этого мотоциклист догнал велосипедиста во второй раз. Найдите скорости велосипедиста и мотоциклиста.
Таким образом, обозначив буквой v (км/час) скорость велосипедиста, получаем, что скорость мотоциклиста равна 5v (км/час).
В условии задачи дано время, прошедшее между двумя последовательными встречами мотоциклиста и велосипедиста, – 46 минут. Это время необходимо выразить в часах, чтобы все единицы измерения были согласованными:
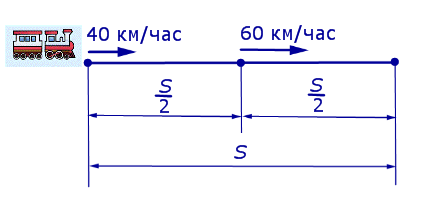
Изобразим данные задачи, касающиеся движения мотоциклиста и велосипедиста между первой и второй встречами, на рисунке 6.
Поскольку за время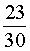 
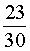
часа, прошедшее от момента первой встречи до момента второй встречи, мотоциклист проехал 46 км (вся круговая трасса) плюс путь, который проехал велосипедист за часа, то можно составить следующее уравнение:
Решая это уравнение, находим скорость велосипедиста:
Если обозначить буквой v (км/час) скорость, с которой велосипедист прошел первый круг, то скорость велосипедиста на втором круге будет равна v – 5 (км/час), и можно составить уравнение
Решая это уравнение, находим скорость велосипедиста на первом круге:
Поскольку скорость велосипедиста на первом круге больше, чем 5 км/час, то первый корень должен быть отброшен.
Желающие ознакомиться с примерами решения различных задач по теме «Проценты» и применением процентов в экономике и финансовой математике могут посмотреть разделы нашего справочника «Проценты. Решение задач на проценты», «Простые и сложные проценты. Предоставление кредитов на основе процентной ставки», а также наши учебные пособия «Задачи на проценты» и «Финансовая математика».
Приемы, используемые для решения задач на выполнение работ представлены в разделе нашего справочника «Задачи на выполнение работ».
С примерами решения задач на смеси, сплавы и растворы можно ознакомиться в разделе нашего справочника «Задачи на смеси, сплавы и растворы».