Что такое скрещивающиеся ребра пирамиды

Теорема о трех перпендикулярах

Что такое теорема о трех перпендикулярах простыми словами

Как ее использовать в задачах

Как оформлять на ЕГЭ

Начнем с парочки вводных понятий, ты же хочешь жить по понятиям?

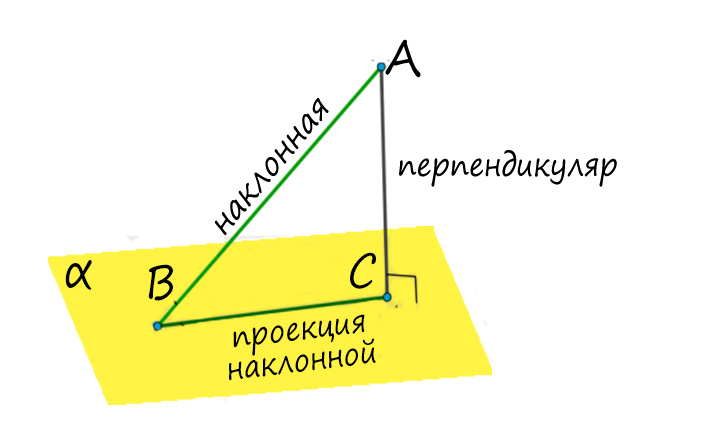
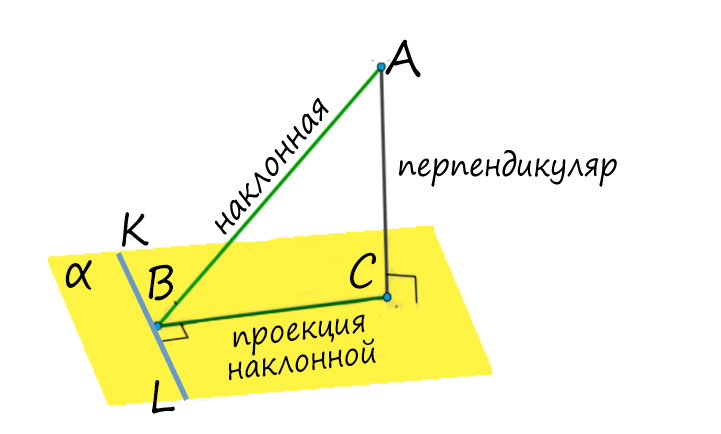
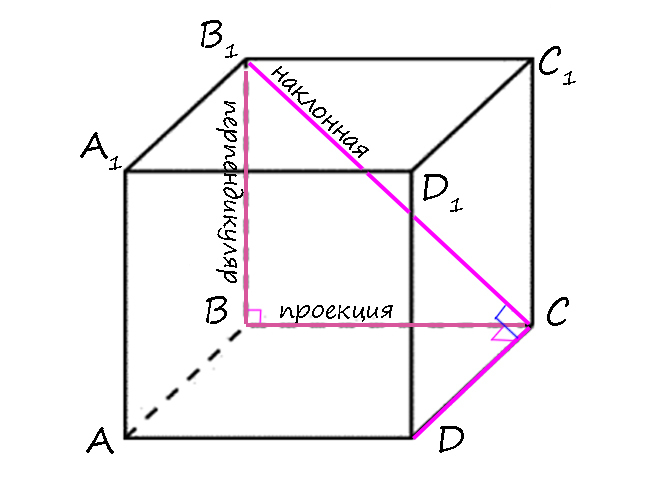
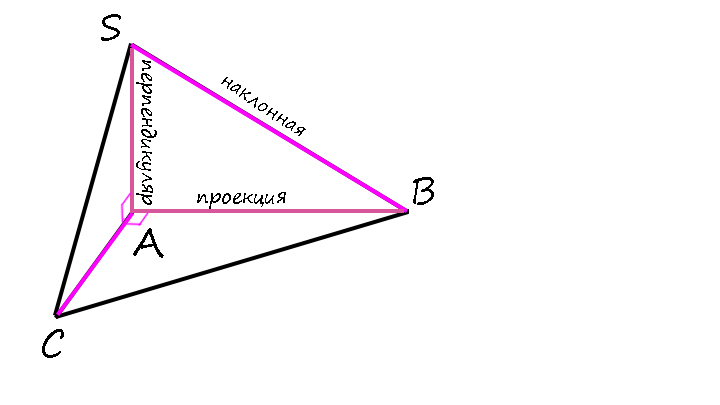
Если в плоскости альфа провести прямую KL через точку В так, что KL ⊥ BC, тогда по теореме о трех перпендикулярах (т.т.п.) KL ⊥ BA.

Словами можно сказать так: прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции этой наклонной на данную плоскость (верно и наоборот).

Перейдем к самому распространенному примеру:

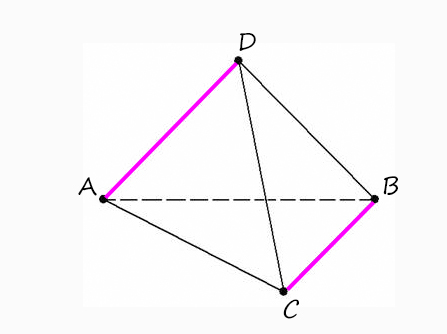
1) Докажите, что в тетраэдре скрещивающиеся ребра перпендикулярны.

У тетраэдра есть три пары скрещивающихся ребер. Докажем перпендикулярность одной пары, другие вы сделаете по аналогии, например, AD ⊥ BC.

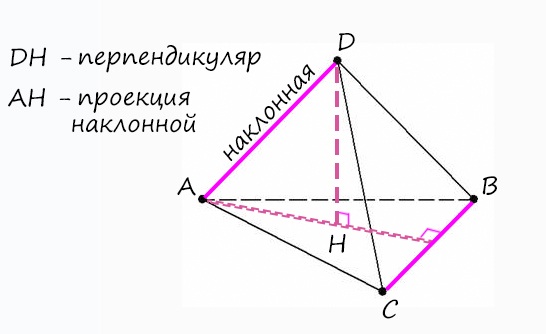
Сейчас есть только наклонная AD и плоскость (ABC), значит, нам не хватает проекции наклонной и перпендикуляра, тогда проведем их:

Тогда, чтобы доказать, что AD ⊥ BC:
1) AH ⊥ BC (если продлить АН до пересечения с BC), т.к. AH является выстой в правильном треугольнике.
2) DH ⊥ (ABC) (по построению, а, значит, перпендикулярно любой прямой, находящейся в этой плоскости) => DH ⊥ BC.

После того, как мы это доказали, можем смело сказать, что AD ⊥ BC (всегда дожно быть доказательство двух пунктов, и только тогда вывод).

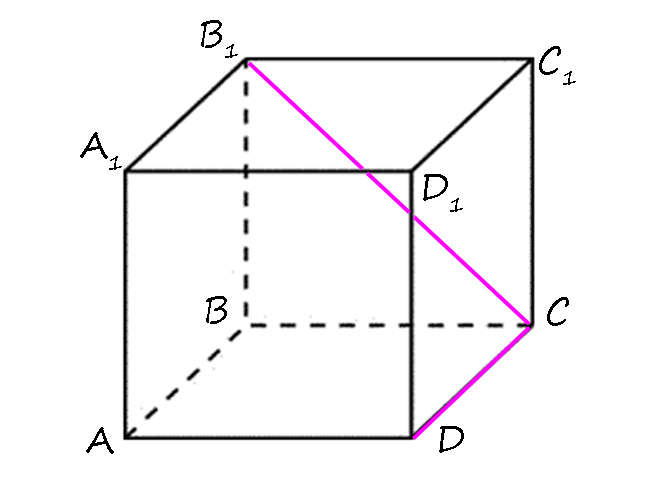
2) Докажите, что в прямом параллепипеде ребра B₁C и CD перпендикулярны.

Возьмем B₁C как наклонную к плоскости (ABCD), тогда перпендикуляром будет BB₁, а проекцией наклонной на эту плоскость — BC.

1) BB₁ ⊥ (ABCD) т.к. параллепипед прямой (боковые ребра перпендикулярны плоскости основания) => BB₁ ⊥ CD (если прямая перпендикулярна плоскости, то и перпендикулярна всем прямым, лежащим в этой плоскости).
2) BC ⊥ CD т.к. ABCD — прямоугольник.
3) По т.т.п.: B₁C ⊥ CD.

Два пункта доказательства, третий пункт вывод.

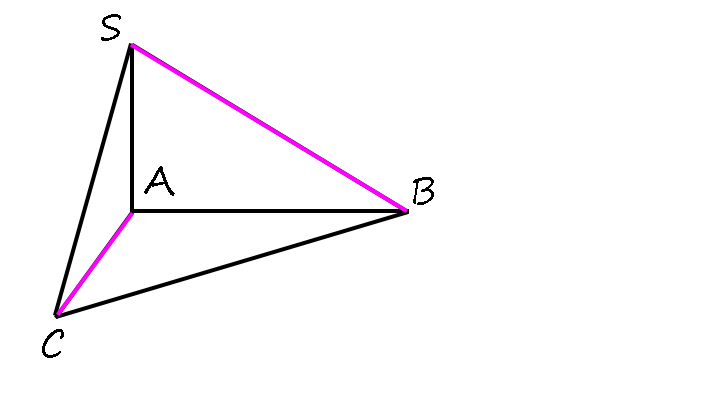
3) Дана пирамида SABC с высотой AS, в основании которой лежит прямоугольный треугольник с прямым углом A. Докажите, что SB⊥ AC.

Скажем, что BC — наклонная к плоскости (ABC):

1) SA ⊥ (ABC) => SA ⊥ AC
2) AB ⊥ AC ( ABC — прямоугольный треугольник по условию).

Вывод:

Два пункта доказательство и вывод!
1) Перпендикуляр будет опускаться на плоскость под 90 °.
2) Проекция наклонной на плоскость перпендикулярна прямой.
3) По т.т.п. наклонная перпендикулярна прямой.

Источник

Что такое пирамида: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения пирамиды. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение пирамиды

Пирамида – это геометрическая фигура в пространстве; многогранник, который состоит из основания и боковых граней (с общей вершиной), количество которых зависит от количества углов основания.

Примечание: пирамида – это частный случай конуса.

Элементы пирамиды

Развёртка пирамиды – фигура, полученная при “разрезе” пирамиды, т.е. при совмещении всех ее граней в плоскости одной из них. Для правильной четырехугольной пирамиды развертка в плоскости основания выглядит следующим образом.

Примечание: свойства пирамиды представлены в отдельной публикации.

Виды сечения пирамиды

1. Диагональное сечение – секущая плоскость проходит через вершину фигуры и диагональ основания. У четырехугольной пирамиды таких сечения два (по одному на каждую диагональ):

2. Если секущая плоскость параллельна основанию пирамиды, она делит ее на две фигуры: подобную пирамиду (считая от вершины) и усеченную пирамиду (считая от основания). Сечением является подобный основанию многоугольник.

Примечание: Существуют и другие виды сечения, но они не так распространены.

Источник

Пирамида и скрещивающиеся прямые

РОССИЙСКАЯ НАУЧНО-СОЦИАЛЬНАЯ ПРОГРАММА

ДЛЯ МОЛОДЕЖИ И ШКОЛЬНИКОВ «ШАГ В БУДУЩЕЕ»

ЧЕЛЯБИНСКИЙ ГОЛОВНОЙ КООРДИНАЦИОННЫЙ ЦЕНТР

«ИНТЕЛЛЕКТУАЛЫ ХХI ВЕКА»

ПИРАМИДА И СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ

Творческая работа на Х VII Челябинскую

городскую научно-практическую конференцию молодых

исследователей и интеллектуалов «Шаг в будущее»

г. Челябинск, лицей № 000, класс 10.

Введение

Оказалось, что энергия формы пирамиды «умеет делать» очень многое: растворимый кофе, постояв над пирамидой, приобретает вкус натурального; дешевые вина значительно улучшают свои вкусовые качества; вода приобретает свойства способствовать заживлению, тонизирует организм, уменьшает воспалительную реакцию после укусов, ожогов и действует, как естественное вспомогательное средство для улучшения пищеварения; мясо, рыба, яйца, овощи, фрукты мумифицируются, но не портятся; молоко долго не киснет; сыр не плесневеет…[6]

Так ли универсальна пирамида? Попытаемся применить эту замечательную фигуру для решения школьных задач.

Мы поставили задачу найти условия, при которых легко можно определить расстояние между скрещивающими прямыми.

Цель работы – найти метод, с помощью которого можно измерять расстояние между скрещивающими прямыми и проверить этот метод для решения практических задач.

Объектом исследования в данной работе являются скрещивающиеся прямые.

Метод исследования – конструирование модели, помогающей определить расположение скрещивающихся прямых в пространстве.

Метод определяет предмет исследования: связь между стереометрическими объектами.

В ходе исследования были найдены условия, при которых поставленная задача решается рациональным способом, а также сформулирован алгоритм применения метода пирамид для решения конкретных задач. В процессе работы изучены существующие методы по данной теме, а также сконструирован удобный и рациональный способ решения данной задачи. Основные понятия

1.1 Скрещивающиеся прямые

На уроках стереометрии в десятом классе мы познакомились со скрещивающимися прямыми.

В этом же учебнике мы читаем о расстоянии между параллельными плоскостями и в п.3 о расстоянии между скрещивающимися прямыми.

Используя эти материалы, мы приступили к решению практических задач. Решения задач были громоздкими и плохо просматривались на рисунках. Поэтому данную тему я решил отыскать в справочниках и других пособиях.

1.2 Методы определения расстояний между скрещивающимися прямыми

Журнал «Математика для школьников» в этом году (№1, 2008г.) опубликовал статью «О расстоянии вообще и расстоянии между скрещивающимися прямыми в частности», где подробно описывает все известные способы построения общего перпендикуляра двух скрещивающихся прямых. Рассматриваются конкретные задачи. В научно-теоретическом и методическом «Математика в школе» (№1,2008г) опубликована статья и «О некоторых способах вычисления расстояния между скрещивающимися прямыми».

Стоит заметить, что задача на построение общего перпендикуляра к двум скрещивающимся прямым требует весьма кропотливой работы. В то же время при нахождении расстояния между скрещивающимися прямыми нет необходимости строить их общий перпендикуляр! Часто бывает достаточно лишь увидеть (провести) более подходящий отрезок, длина которого и будет искомым расстоянием. При этом целесообразно опираться на одно из следующих утверждений.

1. Расстояние между скрещивающимися прмыми равно расстоянию между параллельными плоскостями, проходящими через эти прямые.

2. Расстояние между скрещивающимися прямыми равно расстоянию от одной из них до параллельной ей плоскости, проходящей через вторую прямую.

3. Расстояние 1 между скрещивающимися прямыми, содержащими отрезки АВ и СВ соответственно, можно вычислять по формуле

где -угол между прямыми AB и CD, а -объем треугольной пирамиды ABCD (рис.1)

Подходы, основанные на применении первых двух утверждений, будучи чисто геометрическими, требуют от решающего хорошего пространственного воображения. Однако второй подход иногда выгоднее реализовывать в координатно-векторной форме. В справочной литературе встречается общее уравнение плоскости — в прямо угольной системе координат ,то можно применить известную в курсе аналитической геометрии формулу расстояния от точки M() до плоскости, заданной этим уравнением:

После изученного материала, я приступил к конструированию изучаемого объекта, с помощью стереометрических моделей, имеющегося в кабинете математики.

В результате я нашел рациональный способ решения поставленной задачи.

Разработанный мною способ нахождения расстояния и угла между скрещивающимися прямыми, который условно назван «Метод пирамиды», дает возможность решить задачу быстро и рационально.

Почему «метод пирамиды»? Дело в том, что при решении задач этим способом строится пирамида РАВСD, а смыслом такого построения является утверждение: «Расстояние между скрещивающимися прямыми равно расстоянию от точки, которая является проекцией одной из двух данных скрещивающихся прямых на перпендикулярную к ней плоскость, к ортогональной проекции другой прямой на эту же плоскость».

в журнале «Математика в школе» (№ 6, 1986 год) использовал приведенное утверждение, привел примеры решения задач, но способ построения отличается от «метода пирамиды». Вся последовательность построения состоит из пяти шагов:

1. Пусть прямая и скрещивающиеся и произвольная точка Р принадлежит прямой .

2. Проведем перпендикуляр РА к прямой . Пусть РА и принадлежат плоскости.

3. Проведем из точки М, которая принадлежит прямой , к плоскости перпендикуляр МN. Пусть прямая РN, которая принадлежит плоскости , пересекает прямую в точке В. Проведем перпендикуляры ВС и АD к плоскости так, чтоб ВС=АD, а точки С и D принадлежали одной полуплоcкости и точка С принадлежала прямой . После этого можно утверждать, что четырехугольник АВСD — прямоугольник, а значит параллельна (РСD) по признаку параллельности прямой и плоскости.

4. Задача свелась к нахождению расстояния от прямой к параллельной ей плоскости РСD. Прямая перпендикулярна к (РАD) по признаку перпендикулярности прямой и плоскости; плоскости (АВС) и (РАD) — перпендикулярны по признаку перпендикулярности плоскостей. Прямая СD перпендикулярна (РАD), поскольку прямые СD и параллельны. Плоскости (РАD) и (РСD) перпендикулярны по признаку перпендикулярности плоскостей. Проведем перпендикуляр АК к прямой РD пересечения перпендикулярных плоскостей РАD и РСD. Значит АК будет перпендикуляром и к плоскости (РОС). Итак, отрезок АК, который является высотою прямоугольного треугольника РАD равен расстоянию между скрещивающимися прямыми и .

5. Проведя КL , точка L принадлежит прямой и LF KA, точка F принадлежит прямойполучаем что LЕ—общий перпендикуляр к двум скрещивающимся прямым и . Если же скрещивающимися прямые пересекаются под прямим углом ( совпадает с РD или РD принадлежит ), то задача значительно упрощается, что часто встречается во многих упражнениях. Кстати, не для всех задач необходимо брать точку М. Выше указанный способ достаточно простой, но при помощи такого подхода мгновенно решаются практически все задачи на нахождение расстояния между скрещивающимися прямыми и построение к ним общего перпендикуляра. Угол между скрещивающимся прямыми и можно найти как угол РСD из прямоугольного треугольника РDС.

1. Практическая часть. Построение пирамиды. Вычисление расстояния между скрещивающимися прямыми

3.1 Задача 1. Каждое ребро правильной треугольной призмы равно а. Определите расстояние между стороною основания и скрещивающейся с нею диагональю боковой грани.

Решение.

РВSPCS — правильная треугольная призма. Найдем расстояние между ВS и РС. Проведем:

а) РА ВS,

б) АD ВС, АD= ВС, точка А ВS.

в) АК РD; К . Из ранее доказанного отрезок АК будет равен искомому расстоянию. Применив метод площадей к прямоугольному треугольнику РАD, получаем:

АК= АР *AD:РD = а .

3.2.Задача 2. Ребро правильного тетраэдра равно а. Найдите расстояние между двумя ребрами тетраэдра, которые являются скрещивающимися.

СРQR — правильный тетраэдр. СО — высота тетраэдра. Будем искать расстояние между РС и RQ.

АК= =.

3.3. Задача З. Ребро куба равно а. Найдите кратчайшее расстояние между диагональю куба и диагональю основания куба, которая с нею скрещивается.

Решение:— куб. Будем искать расстояние между РМ и RQ. По ранее доказанному утверждению отрезок АК, который является высотой прямоугольного треугольника РАD будет равен искомому расстоянию:

3.4. Задача 4. Найти расстояние между скрещивающимися диагоналями смежных граней куба.

Решение.

РВQSGCRH — куб. Найдем расстояние между ВS и РС. По ранее доказанному АК является искомым расстоянием:

3.5. Задача 5. Ребро правильной четырехугольной пирамиды равно а. Найти расстояние между диагональю основания и скрещивающейся с нею: а) апофемою; б) высотою боковой грани проведенной из вершины основания.

а) СLQRF — правильная четырехугольной пирамида. Найдем расстояние между QF и CP.

Из прямоугольного прямоугольника DAP: ;

б) SPQRF — правильная четырехугольная пирамида. Найдем расстояние между QF и РС. Как и в предыдущих задачах, все построения выполнены. Остается опустить перпендикуляр СВ на плоскость основания, провести АD=ВС и так, чтобы АDВС. Тогда высота АК прямоугольного треугольника РАD будет искомым расстоянием. Поскольку , то Из прямоугольного треугольника PAD: .

3.6. Задача 6. Ребро правильного тетраэдра равно а. Найдите расстояние между ребром тетраэдра и скрещивающейся с ним апофемой.

Решение.

CPQR— правильный тетраэдр, СВ — его высота. Найдем расстояние между высотой основания RA и боковым ребром СР. АК — расстояние между скрещивающимися СР и RA. Действительно, с помощью метода пирамиды почти все построения уже выполнены, остается построить AD BC, так, чтобы AD=BC тогда высота AK прямоугольного треугольника PAD – искомое расстояние. Из прямоугольных треугольников CBR и PAD имеем ;; ;

Заключение

В результате проделанной работы я пришел к следующим выводам:

Ø Решая задачи по стереометрии целесообразно использовать дополнительные построения;

Ø При определении расстояния между скрещивающимися прямыми предлагаю использовать метод пирамиды.

Литература

2. Журнал «Математика для школьников» №1 2008 год

3. Журнал «Математика в школе» (№ 6, 1986 год)

4. Журнал «Математика в школе,№1,2008год

Источник