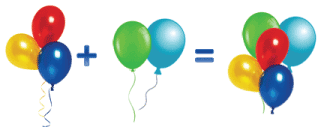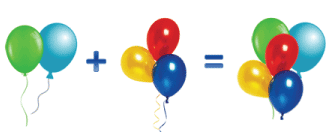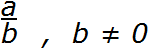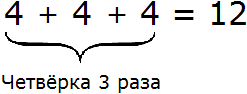Что такое сложение в математике определение
Сложение
Познакомимся со сложением.
Рассмотрим числовой ряд.
Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Посмотри на числовой ряд, по которому идёт заяц.
Какое действие выполняет заяц?
Прибавляет число 2.
К какому числу он прибавляет число 2?
К числу 4.
Наш зайчик стоит на числе 4 и думает, в какую сторону ему идти.
В какую сторону пойдёт зайчик?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает заяц?
2, потому что ему нужно прибавить 2.
На каком делении остановится заяц?
На числе 6.
Когда прибавляем, становится больше.
Чем правее, тем числа больше.
4 + 2 = 6
Рассмотрим еще один пример.
Какое действие выполняет заяц?
Прибавляет число 5.
К какому числу он прибавляет число 5?
К числу 3. Мы поставили зайчика на число 3.
В какую сторону он пойдёт?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает зайчик? 5.
На каком делении он остановится? На числе 8.
3 + 5 = 8
Как называются числа при сложении?
Первое слагаемое и второе слагаемое.
Результат называется суммой.
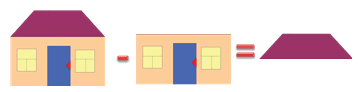
Представь части домика как слагаемые и сумму.
Как найти неизвестное слагаемое
Второе слагаемое неизвестно.
Рассмотри рисунок и догадайся, как его можно найти.
Нужно из суммы вычесть первое слагаемое.
Неизвестно первое слагаемое.
Как его можно найти?
Нужно из суммы вычесть второе слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Проверка сложения
Если из суммы двух слагаемых, вычесть одно из слагаемых, то получится второе слагаемое.
Именно эта связь между суммой и слагаемыми используют для проверки вычислений.
Например, 35 + 7 = 42.
Правильно ли произведено вычисление? Можно проверить так:
Перестановка слагаемых
Сделаем запись к рисунку.
3 + 2 = 5
Сделаем запись к этому рисунку.
2 + 3 = 5
Теперь рассмотрим обе записи к рисункам:
3 + 2 = 5
2 + 3 = 5
Мы заметили, что сумма в обеих записях одинаковая, хотя слагаемые мы записывали по-разному.
Это переместительный закон сложения, который гласит:
От перестановки мест слагаемых сумма не меняется.
Сочетательный закон сложения
1) Какие числа удобно сложить сначала, чтобы получился удобный способ? Числа 29 и 1.
Сумму чисел 29 и 1 возьмем в скобки.
37 + (29 + 1) = … (читаем: к 37 прибавить сумму чисел 29 и 1)
Решаем. Сначала выполним действие в скобках.
Вывод: два соседних слагаемых можно заменить их суммой.
Поделись с друзьями в социальных сетях:
Математика
Определение сложения
Сложение есть такое действие, в котором по двум или нескольким числам находится число, равное всем им, взятым вместе.
Сложение есть соединение двух или нескольких чисел в одно.
Данные числа в сложении называются слагаемыми, а искомое — суммой.
Сумма заключает в себе столько единиц, сколько их содержится во всех слагаемых.
При сложении двух чисел одно число увеличивается на столько единиц, сколько их содержится в другом числе. Сложить одно число с другим значит прибавить одно число к другому.
Знак сложения. Действие сложения обозначается знаком + (плюс).
Сложение однозначных чисел
Чтобы обозначить, что нужно сложить числа 2, 7, 8, 9, 6, пишут эти числа рядом, помещая между ними знак сложения +:
Для сложения прибавляют к первому числу второе, затем к полученному результату прибавляют третье число и т. д., до последнего числа.
Самый ход вычисления выражают письменно:
2 да 7 составляют 9, 9 да 8 составляют семнадцать, 17 да 9 — двадцать шесть, 26 да 6 — тридцать два.
Числа 2, 7, 8, 9, 6 являются слагаемыми, а число 32 есть сумма.
Основное свойство суммы. Сумма не изменится, если мы сложим те же числа в другом порядке, так как в этом случае сумма будет содержать те же самые единицы, следовательно, сумма не изменяется от перемены порядка слагаемых.
На этом свойстве суммы основываются все правила сложения.
Сложение многозначных чисел
Чтобы обозначить, что нужно сложить несколько многозначных чисел (2302, 495, 30) обыкновенно пишут:
Мы можем рассматривать каждое число состоящим из единиц, десятков, сотен и т. д. Зная, что сумма не изменяется от перемены порядка слагаемых, мы можем отдельно складывать между собою единицы с единицами, десятки с десятками, сотни с сотнями и т. д.
Чтобы облегчить сложение, подписывают слагаемые числа одно под другим так, чтобы единицы стояли под единицами, десятки под десятками и т. д., то есть, чтобы цифры одинаковых порядков находились в одном вертикальном столбце. Затем проводим черту, чтобы отделить слагаемые от суммы.
В нашем примере числа должны быть написаны так:
Ход вычисления выражается словесно:
Начинаем сложение с единиц: 2 да 5 составляют семь; подписываем под единицами 7.
Складываем десятки: 9 да 3 составляют 12; 12 десятков составляют одну сотню и 2 десятка; подписываем под десятками цифру 2, а единицу прибавляем к сотням, надписываем ее над сотнями, или как обыкновенно выражаются: замечаем ее в уме.
Складываем сотни: 1 (в уме) да 3 составят 4, 4 да 4 составляют 8; подписываем под сотнями 8.
Складывая тысячи, получаем 2.
Само действие выразится письменно:
Пример. Складывая числа 3275 + 41297 + 135 + 97, имеем:
Из предыдущих примеров выводим правила сложения:
Чтобы сложить целые числа, нужно подписать слагаемые одно под другим так, чтобы единицы одинаковых порядков стояли в одном вертикальном столбце, то есть единицы под единицами, десятки под десятками, сотни под сотнями и т. д., провести черту и отделить таким образом слагаемые от суммы.
Сложение нужно начинать с простых единиц, то есть с первого столбца, и затем, переходя от правой руки к левой к следующим столбцам, складывают десятки с десятками, сотни с сотнями и т. д.
Если при сложении простых единиц получится в сумме 9 или число меньше 9-ти, нужно подписывать его под столбцом единиц. Если же в сумме получится число больше 9, цифру единиц подписывают под столбцом единиц, а число, выражающее десятки, присоединяют к следующему столбцу.
При сложении столбца десятков нужно поступать подобным же образом и продолжать сложение, пока не получим полной суммы.
Сложение
Сложение (прибавление) — одна из основных операций (действий) в разных разделах математики, позволяющая объединить два объекта (в простейшем случае — два числа). Более строго сложение — бинарная операция, определённая на некотором множестве, элементы которого мы будем называть числами, при которой двум числовым аргументам (слагаемым) a и b сопоставляется итог (сумма), обычно обозначаемый с помощью знака «плюс»: a+b.
Содержание
Определение сложения
Абстрактная алгебра
В абстрактной алгебре сложением может называться любая бинарная, коммутативная и ассоциативная операция. В случае, если на этом множестве определено также умножение, то сложение предполагается дистрибутивным по отношению к нему.
Свойства сложения в арифметике
Сложение обладает следующими свойствами:
В других системах (чисел, объектов) любое из этих свойств может не выполняться.
Обозначение операции
Знак плюс для операции сложения плюса (а также знак минуса) придумали в немецкой математической школе «коссистов» (то есть алгебраистов). Они используются в «Арифметике» Иоганна Видмана, изданной в 1489 году. До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus). У Видмана символ плюса заменяет не только сложение, но и союз «и». Происхождение этих символов неясно, но, скорее всего, они ранее использовались в торговом деле как признаки прибыли и убытка. Оба символа вскоре получили общее распространение в Европе — за исключением Италии, которая ещё около века использовала старые обозначения.
Запись при помощи буквы Σ
См. также
Полезное
Смотреть что такое «Сложение» в других словарях:
СЛОЖЕНИЕ — СЛОЖЕНИЕ, сложения, ср. 1. только ед. Действие по гл. сложить во 2, 5 и 7 знач. складывать слагать. Сложение сил (замена нескольких сил одной, производящей равноценное действие; физ.). Сложение величин. Сложение обязанностей. 2. только ед. Одно… … Толковый словарь Ушакова
сложение — См … Словарь синонимов
СЛОЖЕНИЕ — СЛОЖЕНИЕ, сложить, сложный и пр. см. слагать. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
СЛОЖЕНИЕ — одно из четырёх арифметических действий, с помощью которого по двум заданным числам а и b (слагаемым) находят третье число с (сумма, результат), которое обозначают как а + b. При сложении справедливы законы: переместительный (коммутативный) a + b … Большая политехническая энциклопедия
СЛОЖЕНИЕ — арифметическое Действие. Обозначается знаком + (плюс). В области целых положительных чисел (натуральных чисел) в результате сложения по данным числам (слагаемым) находится новое число (сумма), содержащее столько единиц, сколько их содержится во… … Большой Энциклопедический словарь
СЛОЖЕНИЕ — СЛОЖЕНИЕ, арифметическая операция, обозначаемая знаком + (плюс). Ее называют ДВОИЧНОЙ ОПЕРАЦИЕЙ, поскольку для того, чтобы операция имела смысл, необходимы по меньшей мере два числа (или элемента) … Научно-технический энциклопедический словарь
сложение — СЛОЖЕНИЕ, я, ср. 1. см. сложить. 2. Математическое действие, посредством к рого из двух или нескольких чисел (или величин) получают новое, содержащее столько единиц (или величин), сколько было во всех данных числах (величинах) вместе. Задача на с … Толковый словарь Ожегова
СЛОЖЕНИЕ 1 — СЛОЖЕНИЕ 1, я, ср. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
СЛОЖЕНИЕ 2 — СЛОЖЕНИЕ 2, я, ср. То же, что телосложение. Богатырское с. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
сложение — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN addition … Справочник технического переводчика
Сложение (математика)
Сложение (математика)
Сложение (прибавление) — одна из основных операций (действий) в разных разделах математики, позволяющая объединить два объекта (в простейшем случае — два числа). Более строго сложение — бинарная операция, определённая на некотором множестве, элементы которого мы будем называть числами, при которой двум числовым аргументам (слагаемым) a и b сопоставляется итог (сумма), обычно обозначаемый с помощью знака «плюс»: a+b.
Содержание
Определение сложения
Арифметика
В арифметике сложение (прибавление) есть бинарная операция, определённая на множестве натуральных чисел, которая удовлетворяет следующим свойствам:
где a’ обозначает натуральное число следующее за а.
Таблицу сложения см. например для десятичной системы счисления.
Абстрактная алгебра
В абстрактной алгебре сложением может называться любая бинарная коммутативная и ассоциативная операция. В случае, если на этом множестве определено также умножение, то сложение предполагается дистрибутивным по отношению к нему.
Свойства сложения в арифметике
Сложение обладает следующими свойствами:
В других системах (чисел, объектов) любое из этих свойств может не выполняться.
Запись при помощи буквы Σ
См. также
Полезное
Смотреть что такое «Сложение (математика)» в других словарях:
Математика инков — Кипукамайок из книги Гуамана Пома де Айяла «Первая Новая Хроника и Доброе Правление». Слева у ног кипукамайока юпана, содержащая вычисления священного числа для песни «Сумак Ньюста» (в оригинале рукописи рисунок не цветной, а чёрно белый;… … Википедия
Сложение — У этого термина существуют и другие значения, см. Сложение (значения). Сложение (прибавление) одна из основных операций (действий) в разных разделах математики, позволяющая объединить два объекта (в простейшем случае два числа). Более … Википедия
Математика в Древнем Египте — Данная статья часть обзора История математики. Статья посвящена состоянию и развитию математики в Древнем Египте в период примерно с XXX по III век до н. э. Древнейшие древнеегипетские математические тексты относятся к началу II… … Википедия
Математика — Евклид. Деталь «Афинской школы» Рафаэля Математика (от др. греч … Википедия
МАТЕМАТИКА — Математику обычно определяют, перечисляя названия некоторых из ее традиционных разделов. Прежде всего, это арифметика, которая занимается изучением чисел, отношений между ними и правил действий над числами. Факты арифметики допускают различные… … Энциклопедия Кольера
Операция (математика) — У этого термина существуют и другие значения, см. Операция. Операция отображение, ставящее в соответствие одному или нескольким элементам множества (аргументам) другой элемент (значение). Термин «операция» как правило применяется к… … Википедия
Вектор (математика) — Вектор У этого термина существуют и другие значения, см. Вектор … Википедия
Матрица (математика) — У этого термина существуют и другие значения, см. Матрица. Матрица математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет… … Википедия
Кольцо (математика) — У этого термина существуют и другие значения, см. Кольцо. В абстрактной алгебре кольцо это один из наиболее часто встречающихся видов алгебраической структуры. Простейшими примерами колец являются алгебры чисел (целых, вещественных,… … Википедия
Дробь (математика) — У этого термина существуют и другие значения, см. Дробь. 8 / 13 числитель числитель знаменатель знаменатель Две записи одной дроби Дробь в математике число, состоящее из одной или нескольких частей… … Википедия
Основные операции
Основные операции, которые используются в математике это сложение, вычитание, умножение и деление.
Ещё пример. Число 11 меньше, чем число 15. Эту фразу можно записать так:
В математике с помощью отношений можно записывать законы, формулы, уравнения и функции. Можно записать, что одно выражение равно другому, либо какое-то действие недопустимо по отношению к какому-нибудь объекту, числу, закону.
Например, знаменитая фраза «на ноль делить нельзя» записывается так:
Не будем опережать события и забегать вперёд. Просто скажем, что в этом выражении вместо a и b могут стоять любые числа. Но потом говорится, что b не должно быть равным нулю.
Знак равенства = стáвится между величинами и говорит о том, что эти величины равны между собой.
Ещё пример: если один большой арбуз весит 20 кг, а два маленьких арбуза весят по 10 кг каждый, то между арбузом в 20 кг и двумя арбузами по 10 кг можно поставить знак равенства. Это отношение можно прочитать так: «один арбуз весом в 20 килограмм равен весу двух арбузов, каждый из которых весит 10 кг». Ведь 20 кг = 10 кг + 10 кг.
Знак не равно ≠ ставится между величинами тогда, когда они не равны между собой.
Вы можете осмотреться вокруг себя и найти множество примеров отношений, которые можно истолковать с точки зрения математики.
Операция сложения
Операция сложения обозначается знаком «плюс» (+) и используется, когда складывают числа.
Числа, которые складывают называются слагаемыми. Число, которое получается в результате их сложения, называется суммой.
Например, сложим числа 3 и 2.
Записываем 3 + 2 = 5
В этом примере 3 − это слагаемое, 2 − второе слагаемое, 5 − сумма.
В будущем придётся складывать довольно большие числа. Но сложение этих больших чисел в конечном итоге будет сводиться к тому, чтобы сложить маленькие.
Поэтому нужно научиться складывать маленькие числа в диапазоне от 0 до 9. Например:
Можете потренироваться, записав в тетради несколько простых примеров. Поверьте, ничего постыдного в этом нет.
Операция вычитания
Операция вычитания обозначается знаком «минус» (−) и используется когда из одного числа вычитают другое.
Число, из которого вычитают другое число, называется уменьшаемым. Число, которое вычитают из уменьшаемого числа, называется вычитаемым. Число, которое получается в результате, называется разностью.
Например, вычтем из числа 10 число 2.
В этом примере число 10 − это уменьшаемое, число 2 − вычитаемое, а число 8 − разность.
Операция умножения
Обозначается знаком умножения (×) и используется когда одно число умножается на другое. Слово умножение говорит само за себя — какое-то число увеличивается в определенное количество раз, то есть мнóжится.
Например, запись 4 × 3 означает, что четверка в ходе операции умножения будет увеличена в три раза.
Число, которое увеличивают, называется множимым. Число, которое показывает во сколько раз нужно увеличить множимое, называется множителем. Число, которое получается в результате называется произведением.
Например, умножим число 4 на 3.
В этом примере 4 − это множимое, 3 − множитель, 12 − произведение.
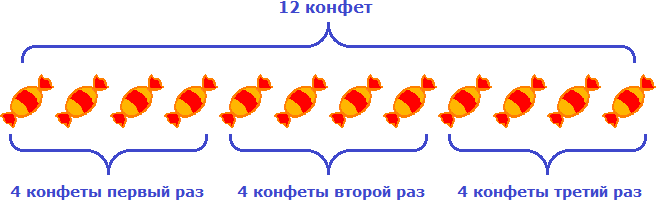
Запись 4 × 3 можно понимать как «повторить число 4 три раза». Например, если у нас имеются четыре конфеты и мы повторим их три раза, то полýчится двенадцать конфет:
Другими словами, умножение 4 на 3 можно представить как сумму трёх четвёрок:
Умножение можно понимать и другим образом, а именно как взятие чего-то определенное количество раз.
Допустим, в вазе лежат конфеты. Возьмём четыре конфеты один раз:
У нас в руках окажется четыре конфеты.
Попробуем взять четыре конфеты 2 раза:
У нас в руках окажется восемь конфет.
Попробуем взять четыре конфеты ноль раз, то есть ни разу:
У нас на руках не окажется конфет, поскольку мы ни разу их не взяли. Поэтому умножение любого числа на ноль даёт в ответе ноль.
В некоторых книгах множимое и множитель называют одним общим словом — сомножители. Например, в записи 4 × 3 множимым является 4, а множителем 3, но эти два числа ещё можно назвать сомножителями. Ошибкой это не будет.
Операция деления
Обозначается знаком деления (÷ или : ) и используется когда делят числа.
Число, которое делят называют делимым. Число, которое указывает на сколько частей делят делимое, называется делителем. Число, которое получается в результате, называется частным.
Например, разделим число 10 на 2.
В этом примере число 10 − это делимое, число 2 − делитель, число 5 − частное.
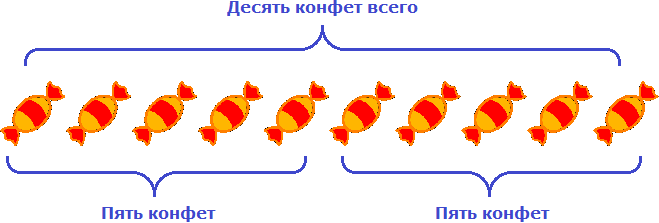
Если у нас имеются десять конфет и мы разделим их на две равные части, то в каждой части полýчится по пять конфет:
Так можно понять смысл записи 10 : 2 = 5.
Задания для самостоятельного решения
Большинство людей решат эти задания в уме что конечно похвально. Однако, рекомендуется выполнить эти задания именно в тетради, взяв в руку карандаш. К математике следует привыкать посредством решения простых примеров.