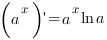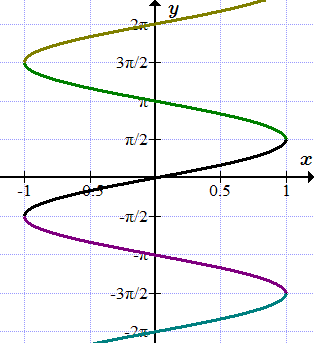Что такое сложная функция определение
Сложная функция. Производная сложной функции.
В этой статье мы будем говорить о таком важном математическом понятии, как сложная функция, и учиться находить производную сложной функции.
Прежде чем учиться находить производную сложной функции, давайте разберемся с понятием сложной функции, что это такое, «с чем ее едят», и «как правильно ее готовить».
Рассмотрим произвольную функцию, например, такую:
Вместо переменной 
мы можем поставить, например, такое выражение: 
. И тогда мы получим функцию
.
Назовем выражение промежуточным аргументом, а функцию 
— внешней функцией. Это не строгие математические понятия, но они помогают уяснить смысл понятия сложной функции.
Строгое определение понятия сложной функции звучит так:
Пусть функция 
определена на множестве 
и 
— множество значений этой функции. Пусть, множество (или его подмножество) является областью определения функции 
. Поставим в соответствие каждому из число 
. Тем самым на множестве будет задана функция 
. Ее называют композицией функций или сложной функцией.
В этом определении, если пользоваться нашей терминологией, — внешняя функция, — промежуточный аргумент.
Производная сложной функции находится по такому правилу:
Чтобы было более понятно, я люблю записывать это правило в виде такой схемы:
В этом выражении с помощью 
обозначена промежуточная функция.
Итак. Чтобы найти производную сложной функции, нужно
1. Определить, какая функция является внешней и найти по таблице производных соответствующую производную.
2. Определить промежуточный аргумент.
В этой процедуре наибольшие затруднения вызывает нахождение внешней функции. Для этого используется простой алгоритм:
а. Запишите уравнение функции.
б. Представьте, что вам нужно вычислить значение функции при каком-то значении х. Для этого вы подставляете это значение х в уравнение функции и производите арифметические действия. То действие, которое вы делаете последним и есть внешняя функция.
Например, в функции
Найдем производную этой функции. Для этого запишем промежуточный аргумент
как
Получим 
Ищем в таблице производных производную показательной функции:
(1)
Теперь наша задача найти производную функции
Смотрим в таблице производных производную синуса:
Подставим полученное значение производной в выражение (1):
И, наконец, упростим выражение, вспомнив формулу синуса двойного аргумента:
Заметим, что функции иногда похожи на матрешку: промежуточный аргумент сам является сложной функции. Но тогда при нахождении производной промежуточного аргумента, нужно вновь применить правило нахождения производной сложной функции.
Определение функции
Определение функции
Сложные функции
Действительные функции
В математическом анализе большую роль играют числовые функции.
Числовая функция – это функция, значениями которой являются действительные или комплексные числа.
Действительная или вещественная функция – это функция, значениями которой являются действительные числа.
Максимум и минимум
Действительные числа имеют операцию сравнения. Поэтому множество значений действительной функции может быть ограниченным и иметь наибольшее и наименьшее значения.
Верхняя и нижняя грани
Монотонные функции
Многозначные функции
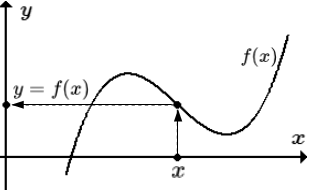
Как следует из определения функции, каждому элементу x из области определения, ставится в соответствие только один элемент из множества значений. Но существуют такие отображения, в которых элемент x имеет несколько или бесконечное число образов.
Многозначная функция – это совокупность функций, определенных на некотором множестве.
Ветвь многозначной функции – это одна из функций, входящих в многозначную функцию.
Однозначная функция – это функция.
Сужение и продолжение функции
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.