Что такое сложное высказывание

сложное высказывание

Смотреть что такое «сложное высказывание» в других словарях:

высказывание контрфактическое — (от лат. contra против, factum событие) сложное высказывание, в котором с помощью союза если бы. то бы. объединяются два высказывания A и В. В естественном языке ему соответствуют предложения, имеющие форму условно сослагательного наклонения … Словарь терминов логики

Высказывание (Предложение) Контрфактическое — (от лат. contra против, factum событие) а сложное высказывание, в котором с помощью союза лесли бы. то бы … Словарь терминов логики

ВЫСКАЗЫВАНИЕ — грамматически правильное повествовательное предложение, взятое вместе с выражаемым им смыслом. В логике употребляется несколько понятий В., существенно различающихся между собой. Прежде всего это понятие дескриптивного, или о п и с а тельного,… … Философская энциклопедия

Сложное синтаксическое целое (сверхфразовое единство, микротекст, период) — группа тесно взаимосвязанных законченных предложений, объединенных общностью темы в смысловой блок. Смысловые отношения, объединяющие самостоятельные предложения в С. с. ц., подкрепляются различными средствами: лексическими (повторение в… … Педагогическое речеведение

таблица истинности — таблица, с помощью которой устанавливается истинностное значение сложного высказывания при данных значениях входящих в него простых высказываний. В классической математической логике предполагается, что каждое простое (не содержащее логических… … Словарь терминов логики

ИМПЛИКАЦИЯ — [лат. implicatio сплетение, переплетение] лог. логическая операция, образующая сложное высказывание из двух высказываний посредством логической связки, соответствующей союзу «если. то. ». Словарь иностранных слов. Комлев Н.Г., 2006. импликация … Словарь иностранных слов русского языка

ИМПЛИКАЦИЯ — (от лат. implicatio сплетение, от implico тесно связываю) логическая связка, соответствующая грамматической конструкции «если. то. », с помощью которой из двух простых высказываний образуется сложное высказывание. В импликативном высказывании… … Философская энциклопедия

Источник

Сложное высказывание

Вы будете перенаправлены на Автор24

Сложное высказывание

Высказывание является одним из ключевых понятий в логике. Точного определения, которое можно было бы использовать в равной мере во всех её разделах, нет. Но можно сказать, что это повествовательное предложение, в котором что-либо утверждается или отрицается. Кроме того, про любое высказывание можно сказать, истинно оно или ложно.

Высказывание будет считаться истинным, если то, что оно описывает соответствует реальной ситуации, и ложным, если описание не соответствует ей.

Из отдельных высказываний можно разными способами выстраивать новые высказывания. Так, из высказываний «Светит солнце» и «Дует ветер» можно образовать сложные высказывания «Светит солнце и дует ветер», «Либо светит солнце, либо дует ветер «, «Если светит солнце, то дует ветер» и т.п. Сложные высказывания образуются при помощи слов «и», «либо, либо», «если, то» и т.п., которые называются логическими связками.

Высказывание является простым, если в нём в качестве своих частей нет других высказываний.

Если высказывание с помощью логических связок получено из нескольких простых высказываний, то оно называется сложным.

В математической логике определены пять основных логических операций: инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность. Три первые операции являются базовыми, составляют полную систему операций, т.е. остальные могут быть нормализованы (выражены через них). В информатике обычно используются именно эти три операции.

Способы построения базовых сложных высказываний

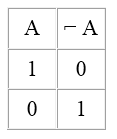
Отрицание (инверсия)

В русском языке этой логической связке соответствует частица НЕ (иногда нужно применить оборот «неверно что. »).

Готовые работы на аналогичную тему

Отрицание (инверсию) можно представить в форме таблицы истинности, в которой «$1$» означает «истинно» и «$0$» – «ложно».

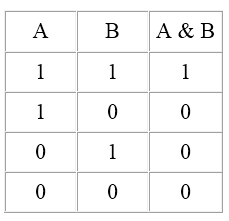
Конъюнкция (логическое умножение)

Если соединить два простых высказывания при помощи связки «и» («но», «а»), то получится сложное высказывание, которое называется конъюнкцией. Простые высказывания, которые соединяются таким способом, называются членами конъюнкции. Например, если высказывания «Вчера было солнечно» и «Сегодня тепло» соединить связкой «и», то получится конъюнкция «Вчера было солнечно и сегодня тепло «.

Конъюнкция истинна тогда и только тогда, когда все её составляющие являются истинными; в противном случае вся конъюнкция ложна.

Если конъюнкцию обозначить символом «&», то таблица истинности для конъюнкции будет выглядеть следующим образом

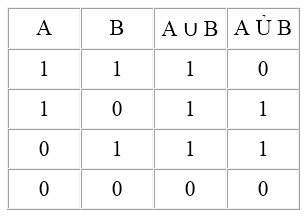
Дизъюнкция

Для формальной логики совершенно не важен смысл простых высказываний. Достаточно знать, являются ли они истинными или ложными. Соединив два высказывания с помощью связки «или», можно получить логическое сложение (дизъюнкцию) этих высказываний. Простые высказывания, которые соединяются таким способом, называются членами дизъюнкции.

Слово «или» в обычном языке имеет два разных смысла. Оно может означать «одно или другое, или оба вместе», а может означать «одно или другое, но не оба вместе». Высказывание «Я хочу в этом сезоне пойти на «Волшебную флейту» или на «Ивана Сусанина» допускает возможность дважды посетить оперу. Высказывание «Он учится в Саратовском или в Московском университете» подразумевает, что студент учится только в одном из заявленных университетов.

Таблица истинности для обоих видов дизъюнкции показывает, что неисключающая дизъюнкция истинна, тогда, когда истинна хотя бы одна из её составляющих; исключающая дизъюнкция истинна тогда, когда истинным является только один из ее членов, во всех остальных случаях она ложна.

Связка «или» в логике и математике всегда употребляется в неисключающем значении.

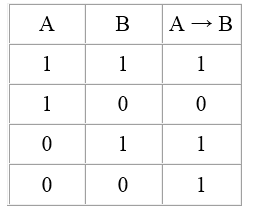
Импликация

Условное высказывание состоит из двух простых высказываний. То, что стоит за словом «если», называется предпосылкой, основанием, условием, или антецедентом (предыдущим); высказывание, которое идёт после слова «то», называется следствием, выводом, или консеквентом (последующим).

Условное высказывание в логике называется импликацией.

Импликация истинна в трех случаях:

когда истинны и ее основание, и ее следствие;

когда условие ложно, а следствие истинно;

когда и предпосылка, и вывод ложны.

И только в одном случае, когда условие истинно, а следствие ложно, вся импликация ложна.

Так, импликация ложна только в одном случае, когда из истинного основания следует ложный вывод.

Эквивалентность

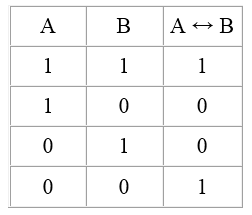
Эквивалентность истинна тогда и только тогда, когда все составляющие ее высказывания либо ложны, либо истинны. Соответственно, эквивалентность является ложной, когда одно из входящих в нее высказываний истинно, а другое ложно.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата написания статьи: 01 04 2016

Источник

Основы алгебры логики

Основные понятия и аксиомы алгебры логики. Простые и сложные высказывания.

Исследования в алгебре логики тесно связаны с изучением высказываний, вызвано это тем, что высказывания являются одним из основных видов носителей информации. С помощью высказываний мы устанавливаем свойства, взаимосвязи между объектами.

Примерами высказываний на естественном языке являются предложения: « Сегодня светит солнце » или « На Красной площади зимой 2007–2008 гг. заливали каток ». Каждое из этих высказываний характеризует свойства или состояние конкретного объекта. Каждое высказывание несет значение « истина » или « ложь ».

Определение. Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности.

Это определение не является математически точным.

Более того, только на первый взгляд оно кажется удовлетворительным. Это определение породило много логических парадоксов.

Причина этого парадокса лежит в структуре построения указанного предложения : оно ссылается на свое собственное значение. С помощью определенных ограничений на допустимые формы высказываний могут быть устранены такие ссылки на себя, и, следовательно, устранены возникающие отсюда парадоксы.

Интересную задачу, содержащую парадокс, придумал знаменитый математик « Известно, что в некотором городе брадобрей бреет всех тех и только тех жителей города, которые не бреются сами. Кто бреет брадобрея? »

Определение. Высказывание называется простым (элементарным), если никакая его часть сама не является высказыванием.

Алгебра логики отвлекается от смысловой содержательности высказываний. Мы можем договориться, что абсурдное по смыслу высказывание: « Крокодилы летают » – является истинным, и с этим значением высказывания будем работать.

Введение таких ограничений дает возможность изучать высказывания алгебраическими методами, т.е. позволяет ввести операции над элементарными высказываниями и с их помощью строить и изучать составные высказывания.

Употребляемые в русском языке связки « и », « или », « не », « если…, то… », « тогда и только тогда, когда … » позволяют из уже заданных высказываний строить новые, более « сложные » высказывания.

Определение. Сложное высказывание – это высказывание, которое состоит из двух или более простых высказываний, объединенных логическими связками.

В алгебре логики логическая операция полностью задается таблицей истинности, указывающей, какие значения принимает сложное высказывание при всех возможных значениях простых высказываний, входящих в сложное высказывание.

Логические операции и соответствующие им логические связки имеют специальные названия и обозначаются следующим образом:

Источник

Сложное высказывание. Виды сложных высказываний

Высказывания отрицания

Среди высказываний отрицания различают высказывания с внешним и внутренним отрицанием. В зависимости от задач исследования высказывание отрицания можно рассматривать или как простое, или как сложное высказывание.

При рассмотрении высказывания отрицания как простого высказывания важной задачей является определение правильной логической формы высказывания:

— простое высказывание, содержащее внутреннее отрицание, принято относить к отрицательным высказываниям (см. «Виды атрибутивных высказывания по качеству»). Например: «Некоторые жители Республики Беларусь не пользуются банковскими кредитами», «Ни один заяц не является хищником»;

— правильной логической формой простого высказывания с внешним отрицанием является противоречащее данному высказывание (см. «Логические отношения между высказываниями. Логический квадрат»). Например: высказыванию «Не все люди жадные» соответствует высказывание «Некоторые люди не являются жадными».

Рассматривая высказывание отрицания как сложное высказывание, необходимо определить его логическое значение.

Исходное высказывание: Солнце светит (р).

Высказывание отрицания: Солнце не светит (┐р).

Высказывание двойного отрицания: Неверно, что солнце не светит (┐┐р).

р	┐р	┐┐р
И	Л	И
Л	И	Л
Рис. 16

Высказывание отрицание истинно лишь тогда, когда исходное высказывание ложно, и наоборот. С высказыванием отрицания связан закон двойного отрицания: двойное отрицание произвольного высказывания равносильно самому этому высказыванию. Условия истинности высказывания отрицания изображены на рис. 16.

Сложным считается высказывание, состоящее из нескольких простых высказываний, соединенных при помощи логических союзов «и», «или», «если…, то…» и т. д. К сложным высказываниям относят соединительные, разделительные, условные, эквивалентные высказывания, а также высказывания отрицания.

Соединительное высказывание (конъюнкция) – это сложное высказывание, состоящее из простых, соединенных при помощи логической связки «и». Логический союз «и» (конъюнкция) может выражаться в естественном языке грамматическими союзами «и», «но», «однако», «а также» и т. д. Например: «Набежали тучи, и пошел дождь», «И большие и малые радуются хорошему дню». На символическом языке логики данные высказывания записываются следующим образом: p∧q. Конъюнкция истинна лишь тогда, когда истинны все ее составляющие простые высказывания (рис. 17).

p	q	Конъюнкция («и»), p∧q	Слабая дизъюнкция («или»), p⋁q	Сильная дизъюнкция («либо»), p⊻q	Импликация («если…, то…»), p→q	Эквиваленция («тогда и только тогда, когда…»), p↔q
И	И	И	И	Л	И	И
И	Л	Л	И	И	Л	Л
Л	И	Л	И	И	И	Л
Л	Л	Л	Л	Л	И	И
Рис. 17

Разделительное высказывание (дизъюнкция). Различают слабую и сильную дизъюнкцию. Слабой дизъюнкции соответствует употребление союза «или» в соединительно-разделительном смысле (или то, или другое, или то и другое вместе). Например: «Этот студент спортсмен или отличник» (p⋁q), «Наследственные факторы, плохая экология и вредные привычки являются причинами большинства заболеваний» (p⋁q⋁r). Слабая дизъюнкция истинна тогда, когда истинно хотя бы одно из входящих в ее состав простых высказываний (см. рис. 17).

Сильной дизъюнкции соответствует употребление союза «либо» в исключающе-разделительном смысле (либо то, либо другое, но не то и другое вместе). Например: «Вечером я буду на занятиях или пойду на дискотеку», «Человек либо жив, либо мертв». Символическая запись p⊻q. Сильная дизъюнкция истинна тогда, когда истинно только одно из входящих в ее состав простых высказываний (см. рис. 17).

Условное высказывание (импликация) – это сложное высказывание, состоящее из двух частей, соединенных с помощью логического союза «если…, то…». Высказывание, стоящее после частицы «если», называют основанием, а высказывание, стоящее после «то» – следствием. При логическом анализе условных высказываний основание импликации всегда ставится вначале. В естественном языке это правило часто не соблюдается. Пример условного высказывания: «Если ласточки низко летают, то будет дождь» (p→q). Импликация ложна лишь в одном случае, когда ее основание истинно, а следствие – ложно (см. рис. 17).

Эквивалентное высказывание – это высказывание, состоящее из простых, соединенных с помощью логического союза «тогда и только тогда, когда» («если и только если…, то…). В эквивалентном высказывании подразумевается одновременное наличие или отсутствие двух ситуаций. В естественном языке эквиваленция может выражаться грамматическими союзами «если…, то…», «лишь в том случае, когда…» и т. д. Например: «Наша команда выиграет лишь в том случае, если хорошо подготовится» (p↔q). Эквивалентное высказывание будет истинным тогда, когда составляющие его высказывания являются либо одновременно истинными, либо одновременно ложными (см. рис. 17).

Для формализации рассуждения необходимо:

1) найти и обозначить малыми согласными буквами латинского алфавита простые высказывания, входящие в состав сложного. Переменные присваиваются произвольно, но если одно и то же простое высказывание встречается несколько раз, то столько же раз используется соответствующая переменная;

2) найти и обозначить логическими константами логические союзы (∧, ⋁, ⊻, →. ↔, ┐);

3) в случае необходимости расставить технические знаки [. ], (. ).

На рис. 18 изображен пример формализации сложного высказывания.

Я уже освободился (p) и (∧), если меня не задержат (┐q) или (⋁)не сломается автомобиль (┐r), то(→) я скоро приеду (s).

После того как высказывание записано в символическом виде, можно определить тип формулы. В логике различают тождественно-истинные, тождественно-ложные и нейтральные формулы. Тождественно-истинные формулы независимо от значений входящих в их состав переменных всегда принимают значение «истина», а тождественно-ложные – значение «ложно». Нейтральные формулы принимают как значение «истина», так и значение «ложно».

Для определения типа формулы используется табличный способ, сокращенный способ проверки формулы на истинность методом «сведения к абсурду» и приведение формулы к нормальной форме. Нормальной формой некоторой формулы является такое ее выражение, которое соответствует следующим условиям:

— не содержит знаков импликации, эквиваленции, строгой дизъюнкции и двойного отрицания;

— знаки отрицания находятся только при переменных.

Табличный способ определения типа формулы:

1. Строят столбцы входных значений для каждой из имеющихся переменных. Эти столбцы называют свободными (независимыми), в них учитывают все возможные комбинации значений переменных. Если в формуле две переменные, то строят два свободных столбца, если же три переменные, то три столбца и т. д.

2. Для каждой подформулы, то есть части формулы, содержащей хотя бы один союз, строят столбец ее значений. При этом учитываются значения свободных столбцов и особенности логического союза (см. рис. 17).

3. Строят столбец выходных значений для всей формулы в целом. По значениям, полученным в выходном столбце, определяют тип формулы. Так, если в выходном столбце имеется только значение «истина», то формула будет относиться к тождественно-истинным и т.д.

Таблица истинности для формулы (p ^ q) → r
p	q	r	p ^ q	(p ^ q) → r
И	И	И	И	И
Л	И	Л	Л	И
Л	Л	И	Л	И
И	Л	Л	Л	И
И	И	Л	И	Л
И	Л	И	Л	И
Л	И	И	Л	И
Л	Л	Л	Л	И
Рис. 19

Число столбцов в таблице равняется сумме переменных, входящих в формулу, и имеющихся в ней союзов. (Например: в формуле на рис. 18 четыре переменных и пять союзов, следовательно, в таблице будет девять столбцов).

На рис. 19 изображен пример таблицы истинности.

Сокращенный способ проверки формулы на истинность методом сведения к абсурду:

1. Предположим, что данная формула не является тождественно-истинной. Следовательно, при некотором наборе значений она принимает значение «ложно».

2. Данная формула может принимать значение «ложно» только в том случае, если основание импликации (p⋁q)⋁r будет «истинно», а следствие p⋁(q⋁r) – «ложно».

3. Следствие импликации p⋁(q⋁r) будет ложным в том случае, когда р – «ложно» и q⋁r – «ложно» (см. значение слабой дизъюнкции на рис. 17).

4. Если q⋁r – «ложно», то и q и r – «ложно».

5. Мы установили что р – «ложно», q – «ложно» и r – «ложно». Основание импликации (p⋁q)⋁r представляет собой слабую дизъюнкцию этих переменных. Так как слабая дизъюнкция принимает значение «ложно» тогда, когда ложными являются все ее составляющие, то основание импликации (p⋁q)⋁r тоже будет «ложным».

6. В п. 2 установили, что основание импликации (p⋁q)⋁r – «истинно», а в п. 5 что оно является «ложным». Возникшее противоречие свидетельствует о том, что предположение, сделанное нами в п. 1, ошибочно.

7. Так как данная формула ни при каком наборе значений своих переменных не принимает значение «ложно», то она является тождественно-истинной.

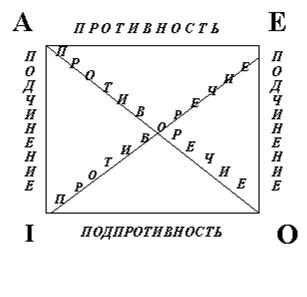
3.8. Логические отношения между высказываниями
(логический квадрат)

Между высказываниями, имеющими сходный смысл, устанавливаются связи. Рассмотрим отношения между простыми и сложными высказываниями.

В логике всю совокупность высказываний разделяют на сравнимые и несравнимые. Несравнимыми среди простых высказываний являются высказывания, имеющие различные субъекты или предикаты. Например: «Все студенты – учащиеся» и «Некоторые студенты – отличники».

Сравнимыми являются высказывания с одинаковыми субъектами и предикатами и различающиеся связкой и квантором. Например: «Все граждане Республики Беларусь имеют право на отдых» и «Ни один гражданин Республики Беларусь не имеет право на отдых».

Рис. 20

Отношения между сравнимыми высказываниями выражаются с помощью модели, которую называют логический квадрат (рис. 20).

Среди сравнимых высказываний различают совместимые и несовместимые.

Отношение совместимости означает, что высказывания могут быть одновременно истинными:

1. Эквивалентность (полная совместимость) – высказывания, которые имеют одинаковые логические характеристики: одинаковые субъекты и предикаты, однотипную утвердительную или отрицательную связку, одну и ту же логическую характеристику. Эквивалентные высказывания различаются словесным выражением одной и той же мысли. С помощью логического квадрата отношения между данными высказываниями не иллюстрируются.

2. Частичная совместимость (подпротивность, субконтрарность). В этом отношении находятся частноутвердительное и частноотрицательное высказывания (I и О). Это означает, что два таких высказывания могут быть одновременно истинными, но не могут быть одновременно ложными. Если одно из них ложно, то второе обязательно истинно. Если же одно из них истинно, то второе неопределенно.

3. Подчинение (субординация). В этом отношении находятся общеутвердительное и частноутвердительное высказывания (А и I), а также общеотрицательное и частноотрицательное высказывания (Е и О).

Из истинности общего высказывания всегда следует истинность частного. В то время как истинность частного высказывания свидетельствует о неопределенности общего высказывания.

Из ложности частного высказывания всегда следует ложность общего высказывания, но не наоборот.

Отношение несовместимости. Несовместимыми являются высказывания, которые не могут быть одновременно истинными:

1. Противоположность (противность, контрарность) – в этом отношении находятся общеутвердительное и общеотрицательное высказывания (А и Е). Это отношение означает, что два таких высказывания не могут быть одновременно истинными, но могут быть одновременно ложными. Если одно из них истинно, то второе обязательно – ложно. Если же одно из них ложно, то второе неопределенно.

2. Противоречие (контрадикторность) – в нем находятся обще-утвердительное и частноотрицательное высказывания (A и О), а также общеотрицательное и частноутвердительное высказывания (Е и I). Два противоречащих высказывания не могут быть ни одновременно ложными, ни одновременно истинными. Одно обязательно истинно, а другое ложно.

Сравнимыми среди сложных высказываний являются высказывания, имеющие хотя бы одну одинаковую составляющую. В противном случае сложные высказывания несравнимы.

Сравнимые сложные высказывания могут быть совместимыми или несовместимыми.

Отношение совместимости означает, что высказывания могут быть одновременно истинными:

1. Эквивалентность: высказывания принимают одни и те же значения, т. е. являются либо одновременно ложными, либо одновременно истинными (рис. 21). Отношение эквивалентности позволяет выражать одни сложные высказывания через другие.

p	q	p→q	┐q→┐p
И	И	И	И
И	Л	Л	Л
Л	И	И	И
Л	Л	И	И
Рис. 21

2. Частичная совместимость означает, что высказывания могут быть одновременно истинными, но не могут быть одновременно ложными (рис. 22).

p	q	p→q	q→p
И	И	И	И
И	Л	Л	И
Л	И	И	Л
Л	Л	И	И
Рис. 22

3. Отношение следования (подчинения) означает, что из истинности одного высказывания следует истинность другого, но не наоборот (рис. 23).

p	q	r	(p→q)∧(q→r)	p↔r
И	И	И	И	И
И	И	Л	Л	Л
И	Л	И	Л	И
Л	И	И	И	И
И	Л	Л	Л	Л
Л	И	Л	Л	И
Л	Л	И	И	И
Л	Л	Л	И	И
Рис. 23

4. Отношение сцепления означает, что истинность (ложность) одного высказывания не исключает ложности (истинности) другого (рис. 24).

p	q	p→q	┐p→q
И	И	И	И
И	Л	Л	И
Л	И	И	И
Л	Л	И	Л
Рис. 24

Отношение несовместимости означает, что высказывания не могут быть одновременно истинными:

1. Противоположность – отношение между высказываниями, которые не могут быть одновременно истинными, но могут быть одновременно ложными (рис. 25).

p	q	p∧q	p∧┐q
И	И	И	Л
И	Л	Л	И
Л	И	Л	Л
Л	Л	Л	Л
Рис. 25

2. Противоречие – отношение между высказываниями, которые не могут быть ни одновременно истинными, ни одновременно ложными (рис. 26).

p	q	p→q	p∧┐q
И	И	И	Л
И	Л	Л	И
Л	И	И	Л
Л	Л	И	Л
Рис. 26

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник