Что такое сложные проценты в математике
Сложные проценты. Примеры вычисление сложных процентов
Формула вычисления сложных процентов
Вывод формулы вычисления сложных процентов
Примеры решения задач на вычисление сложных процентов
Решение: Используем формулу для вычисления сложных процентов:
Ответ: прибыль 9930 рублей.
Решение:
Если положить в банк A рублей, то черех год получим:
| B = A(1 + | 12% | ) |
| 100% |
Если проценты начислялись каждый месяц с процентной ставкой х, то по формуле сложных процентов через год (12 месяцев)
| B = A(1 + | x | ) 12 |
| 100% |
Приравняв эти величины получим уравнение, решение которого позволит определить месячную процентную ставку
| A(1 + | 12% | ) = A(1 + | x | ) 12 |
| 100% | 100% |
| 1.12 = (1 + | x | ) 12 |
| 100% |
x = ( 12 √
Ответ: месячная процентная ставка равна 0.9488792934583046%.
N.B. Из решения этой задачи можно видеть, что месячная процентная ставка не равна годовой ставке поделенной на 12.
а) Для первого случая используем формулу для вычисления сложных процентов:
б) Для первого случая используем формулу для вычисления сложных процентов:
Что такое сложный процент? Как рассчитать — формула сложных процентов с примерами
Каждый из нас изучал на уроках математики сложные проценты. Некоторые даже постигали их на парах по экономике в университете. Но, как обычно, бывает, больше о них мы не думали. А зря. Они нужны во взрослой жизни всем, кто занимается, например, планированием семейного бюджета на ближайший год, решая открыть депозитный счет, или выбирает подходящий инвестиционный проект для вложения денег. Так что же это такое? В чем особенность и как его рассчитать? Сейчас подробно расскажу, приведу формулы с примерами расчетов.
Сложный процент — что это? Пример
Предлагаю рассмотреть это на примере. Так будет намного удобнее и доходчивее. Предположим, что вы положили 10 000 рублей в банк на депозитный счет под 10% годовых на 10 лет, без ежемесячных взносов. Через год у вас будет 11 000 рублей. Если прибыль не трогать и оставить на счете, то на следующий год начисления будут производиться от 11 000. Тогда доход составит 1100 рублей, вместо 1000. Спустя 10 лет, следуя этому принципу, у вас будет уже без малого 26 000 рублей.
| Год | Базовая сумма начисления | % по депозиту | Итоговая сумма с учетом % |
| 1 | 10000.00 | 1000.00 | 11000.00 |
| 2 | 11000.00 | 1100.00 | 12100.00 |
| 3 | 12100.00 | 1210.00 | 13310.00 |
| 4 | 13310.00 | 1331.00 | 14641.00 |
| 5 | 14641.00 | 1464.10 | 16105.10 |
| 6 | 16105.10 | 1610.51 | 17715.61 |
| 7 | 17715.61 | 1771.56 | 19487.17 |
| 8 | 19487.17 | 1948.72 | 21435.89 |
| 9 | 21435.89 | 2143.59 | 23579.48 |
| 10 | 23579.48 | 2357.95 | 25937.43 |
| Итого | 15937.43 | 25937.43 |
Все расчеты приведены в таблице для большей наглядности.
Думаю, комментарии излишни. Вы сами прекрасно видите отличие первого варианта от второго. Как одно маленькое условие может кардинально изменить итоговую сумму. Процентная ставка одна и та же, а вот начисления по сложным процентам намного выгоднее, чем по простым. Еще лучше заметна эта разница на графике.
Рост доходности по простым % линейный, а вот по сложным экспоненциальный. Лучше всего это проявляется на длинном промежутке времени. Когда начальный капитал увеличивается в объемах, словно снежный комок. Из периода в период сумма прибыли становится все больше и больше. Способствует этому то, что сама прибыль накапливается и производит новую.
«Сложный процент — это чудо, восьмое чудо света.» Ротшильд
Формула сложных процентов
Теперь давайте приступим к самому важному. Узнаем наконец-то, как всё это рассчитывается. Формула имеет следующий вид:
Воспользуемся данной формулой на практике.
Пример 1. Вы положили на депозит в банке 60 000 рублей под 12% годовых на 8 лет. Узнать, какую сумму вы получите через 8 лет, можно с помощью вышеупомянутой формулы:
S = 60 000 * (1 + 12/100)^8 = 148 557 руб.
Размер итоговой прибыли может зависеть от различных факторов. Например, от того, как начисляются проценты ежемесячно или раз в год. Тогда формула немного видоизмениться.
Пример 2. Пусть условие остается прежним из Примера 1, но начисления будут происходить каждый месяц.
S = 60 000 * (1 + 12/100/12)^96 = 155 956 руб.
Думаю, понятно, откуда появилось число 96 — это 8 лет умноженные на 12 месяцев. А процентную ставку i необходимо ещё разделить на 12 (месяцев). Тогда формула для наращения процентов m раз в году примет вид:
где m = 365, при ежедневном начислении прибыли, m = 12 — ежемесячном, m = 4 — ежеквартальном, m = 2 — полугодовом.
Как видно из примеров, чем чаще начисления, тем конечный доход будет выше. Только важно помнить главное правило — сложные % тогда будут приносить реальную пользу, когда вы не будете снимать получаемую с них прибыль.
«Сложные проценты — это величайшее математическое открытие.» А.Эйнштейн
Заключение
Даже спустя сотни лет после открытия, сложные проценты не теряют своей популярности и значимости. Это мощный инструмент в финансовом мире для приумножения капитала. Не имеет значения являетесь вы крупным инвестором или просто держите депозитный счет в банке. Более важным будет ваше мастерство находить самые выгодные предложения.
Согласитесь, ведь куда лучше сделать вклад с меньшей процентной ставкой, но с возможностью капитализации доходов. Чем положить деньги с высокой ставкой, но без такого преимущества.
Как решать задачи с процентами
Основные определения
Когда мы сравниваем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе.
Чтобы сравнивать сотые доли, придумали процент (1/100): с латинского языка — «за сто».
Процент — это одна сотая часть от любого числа. Обозначается вот так: %.
Как перевести проценты в десятичную дробь? Нужно убрать знак % и разделить число на 100. Например, 18% — это 18 : 100 = 0,18.
А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например:
Выразить дробь в процентах просто. Для перевода сначала превратим ее в десятичную дробь, а потом используем предыдущее правило и переведем десятичную дробь в проценты:
Типы задач на проценты
В 5, 6, 7, 8, 9 классах в задачках по математике на проценты сравнивают части одного целого, определяют долю части от целого, ищут целое по части. Давайте рассмотрим все виды задач на проценты.
Тип 1. Нахождение процента от числа
Чтобы найти процент от числа, нужно число умножить на процент.
Задача. За месяц на заводе изготовили 500 стульев. 20% изготовленных стульев не прошли контроль качества. Сколько стульев не прошло контроль качества?
Как решаем: нужно найти 20% от общего количества изготовленных стульев (500).
Ответ: из общего количества изготовленных стульев контроль не прошли 100 штук.
Тип 2. Нахождение числа по его проценту
Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.
Задачи по поиску процента по числу и числа по его проценту очень похожи. Чтобы не перепутать — внимательно читаем условия, иначе зайдем в тупик или решим неправильно. Если в задании есть слова «который», «что составляет» и «который составляет» — перед нами задача по нахождению числа по его проценту.
Задача. Школьник решил 40 задач из учебника. Что составляет 16% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?
Как решаем: мы не знаем, сколько всего задач в учебнике. Но нам известно, что 40 задач составляют 16% от общего количества. Запишем 16% в виде дроби: 0,16. Далее известную нам часть целого разделим на ту долю, которую она составляет от всего целого.
40 : 0,16 = 40 · 100 : 16 = 250
Ответ: 250 задач собрано в этом учебнике.
Тип 3. Нахождение процентного отношения двух чисел
Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.
Задача. В классе учится 25 человек. 10 из них — девочки. Сколько процентов девочек в классе?
Как решаем: поделим 10 на 25, полученную дробь переведем в проценты.
10/25 * 100% = 2/5 * 100% = 2 * 100/5 = 40%
Ответ: в классе 40% девочек.
Тип 4. Увеличение числа на процент
Чтобы увеличить число на некоторое количество процентов, можно найти число, которое выражает нужное количество процентов от данного числа, и сложить его с данным числом.
А можно воспользоваться формулой:
где a — число, которое нужно найти,
b — первоначальное значение,
c — проценты.
Задача. В прошлом месяце стикерпак стоил 110 рублей. А в этом месяце на 12% больше. Сколько стоит стикерпак?
Как решаем: можно найти 12% от 110:
Прибавить к исходному числу:
110 + 13,2 = 123,2 рубля.
Или можно воспользоваться формулой, тогда:
110 · (1 + 12 : 100) = 110 · 1,12 = 123,2.
Ответ: стоимость стикерпака в этом месяце — 123 рубля 20 копеек.
Тип 5. Уменьшение числа на процент
Чтобы уменьшить число на несколько процентов, можно найти число, которое выражает нужное количество процентов данного числа, и вычесть его от данного числа.
А можно воспользоваться формулой:
где a — число, которое нужно найти,
b — первоначальное значение,
c — проценты.
Задача. В прошлом году школу закончили 100 ребят. А в этом году выпускников на 25% меньше. Сколько выпускников в этом году?
Как решаем: можно найти 25% от 100:
Вычесть из исходного числа 100 − 25 = 75 человек.
Или можно воспользоваться формулой, тогда:
100 · (1 − 25 : 100) = 75/p>
Ответ: 75 выпускников в этом году.
Тип 6. Задачи на простые проценты
Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада или долга.
Формула расчета выглядит так:
S = а · (1 + у · х : 100),
где a — исходная сумма,
S — сумма, которая наращивается,
x — процентная ставка,
y — количество периодов начисления процента.
Задача. Марии срочно понадобились деньги и она взяла на один год в долг 70 000 рублей под 8% ежемесячно. Сколько денег она вернет через год?
Как решаем: подставим в формулу данные из условий задачи.
70 000 · (1 + 12 · 8 : 100) = 137 200
Ответ: 137 200 рублей вернет Мария через год.
Тип 7. Задачи на сложные проценты
Сложные проценты — это метод расчета процентов, когда проценты прибыли прибавляют к сумме на остатке каждый месяц. В следующий раз проценты начисляют на эту новую сумму.
Формула расчета выглядит так:
где S — наращиваемая сумма,
a — исходная,
x — процентная ставка,
y — количество периодов начисления процента.
Задача. Антон хочет оформить вклад 10 000 рублей на 5 лет в банке, который дает 10% годовых. Какую сумму снимет Антон через 5 лет хранения денег в этом банке?
Как решаем: просто подставим в формулу данные из условий задачи:
10000 · (1 + 10 : 100)3 = 13 310
Ответ: 13 310 рублей снимет Антон через год.
Курсы по математике для учеников с 1 по 11 классы. Вводный урок — бесплатно!
Есть случаи, когда найти процент от числа проще, если представить проценты в виде простых дробей. В таком случае будем искать часть числа.
Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?
Ответ: средств хватит, так как пиджак стоит 6375 рублей.
Задачи на проценты с решением
Как мы уже убедились, решать задачи на проценты совсем несложно. Для закрепления материала рассмотрим реальные примеры на проценты из учебников и несколько заданий для подготовки к ЕГЭ.
Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?
Ответ: масса воды 53,2 кг
Задача 2. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?
Обозначим первоначальную цену товара через х. После первого понижения цена станет равной.
Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения получим:
После двух понижений изменение цены составит:
Так как величина 0,55x составляет 55% от величины x, то цена товара понизилась на 55%.
Задача 3. Четыре пары брюк дешевле одного пальто на 8%. На сколько процентов пять пар брюк стоят дороже, чем одно пальто?
По условиям задачи стоимость четырех пар брюк — это 92% от стоимости пальто
Получается, что стоимость одной пары брюк — это 23% стоимости пальто.
Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто.
Ответ: пять пар брюк на 15% дороже, чем одно пальто.
Задача 4. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Вычислить, какой процент в общий доход семьи приносит заработок жены.
По условиям задачи общий доход семьи напрямую зависит от доходов мужа. Благодаря увеличению зарплаты общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз 67% от общего дохода.
Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 — это и есть 4%, на которые уменьшился бы семейных доход.
Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии — это 4% дохода, то вся стипендия — это 6%.
А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100 – 67 – 6 = 27.
Ответ: заработок жены составляет 27%.
Задача 5. В свежих абрикосах 90% влаги, а в сухофрукте кураге только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?
Исходя из условия, в абрикосах 10% питательного вещества, а в кураге в концентрированном виде — 95%.
Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества.
Значит, 19 килограммов питательного вещества в абрикосах — это 10% веса свежих абрикосов. Найдем число по проценту.
Ответ: 190 кг свежих абрикосов потребуется для изготовления 20 кг кураги.
Сложный процент
Сложным процентом принято называть эффект, когда проценты прибыли прибавляются к основной сумме и в дальнейшем сами участвуют в создании новой прибыли.
Формула сложного процента — это формула, по которой рассчитывается итоговая сумма с учётом капитализации (начислении процентов).
Простой расчет сложных процентов
Чтобы лучше усвоить расчет сложных процентов, давайте разберём пример.
Представим, что вы положили 10 000 руб в банк под 10 процентов годовых.
Через год на вашем банковском счету будет лежать сумма SUM = 10000 + 10000*10% = 11 000 руб.
Ваша прибыль — 1000 рублей.
Вы решили оставить 11 000 руб на второй год в банке под те же 10 процентов.
Через 2 года в банке накопится 11000 + 11000*10% = 12 100 руб.
Прибыль за первый год (1000 рублей) прибавилась к основной сумме (10000р) и на второй год уже сама генерировала новую прибыль. Тогда на 3-й год прибыль за 2-й год прибавится к основной сумме и будет сама генерировать новую прибыль. И так далее.
Этот эффект и получил название сложный процент.
Когда вся прибыль прибавляется к основной сумме и в дальнейшем уже сама производит новую прибыль.
Формула сложного процента:
SUM = X * (1 + %) n
где
SUM — конечная сумма;
X — начальная сумма;
% — процентная ставка, процентов годовых /100;
n — количество периодов, лет (месяцев, кварталов).
Расчет сложных процентов: Пример 1.
Вы положили 50 000 руб в банк под 10% годовых на 5 лет. Какая сумма будет у вас через 5 лет? Рассчитаем по формуле сложного процента:
SUM = 50000 * (1 + 10/100) 5 = 80 525, 5 руб.
Сложный процент может использоваться, когда вы открываете срочный вклад в банке. По условиям банковского договора процент может начисляться например ежеквартально, либо ежемесячно.
Расчет сложных процентов: Пример 2.
Рассчитаем, какая будет конечная сумма, если вы положили 10 000 руб на 12 месяцев под 10% годовых с ежемесячным начислением процентов.
SUM = 10000 * (1+10/100/12) 12 = 11047,13 руб.
ПРИБЫЛЬ = 11047,13 — 10000 = 1047,13 руб
Доходность составила (в процентах годовых):
% = 1047,13 / 10000 = 10,47 %
То есть при ежемесячном начислении процентов доходность оказывается больше, чем при начислении процентов один раз за весь период.
Если вы не снимаете прибыль, тогда начинает работать сложный процент.
Формула сложного процента для банковских вкладов
На самом деле формула сложного процента применительно к банковским вкладам несколько сложнее, чем описана выше. Процентная ставка для вклада (%) рассчитывается так:
% = p * d / y
где
p — процентная ставка (процентов годовых / 100) по вкладу,
например, если ставка 10,5%, то p = 10,5 / 100 = 0,105;
d — период (количество дней), по итогам которого происходит капитализация (начисляются проценты),
например, если капитализация ежемесячная, то d = 30 дней
если капитализация раз в 3 месяца, то d = 90 дней;
y — количество дней в календарном году (365 или 366).
То есть можно рассчитывать процентную ставку для различных периодов вклада.
Формула сложного процента для банковских вкладов выглядит так:
При расчете сложных процентов нужно принимать во внимание тот факт, что со временем наращивание денег превращается в лавину. В этом привлекательность сложных процентов. Представьте себе маленький снежный комок размером с кулак, который начал катиться со снежной горы. Пока комок катится, снег налипает на него со всех сторон и к подножию прилетит огромный снежный камень. Также и со сложным процентом. Поначалу прибавка, создаваемая сложным процентом, почти незаметна. Но через какое-то время она показывает себя во всей красе. Наглядно это можно увидеть на примере ниже.
Расчет сложных процентов: Пример 3.
Рассмотрим 2 варианта:
1. Простой процент. Вы инвестировали 50 000 руб на 15 лет под 20%. Дополнительных взносов нет. Всю прибыль вы снимаете.
2. Сложный процент. Вы инвестировали 50 000 руб на 15 лет под 20%. Дополнительных взносов нет. Каждый год проценты прибыли прибавляются к основной сумме.
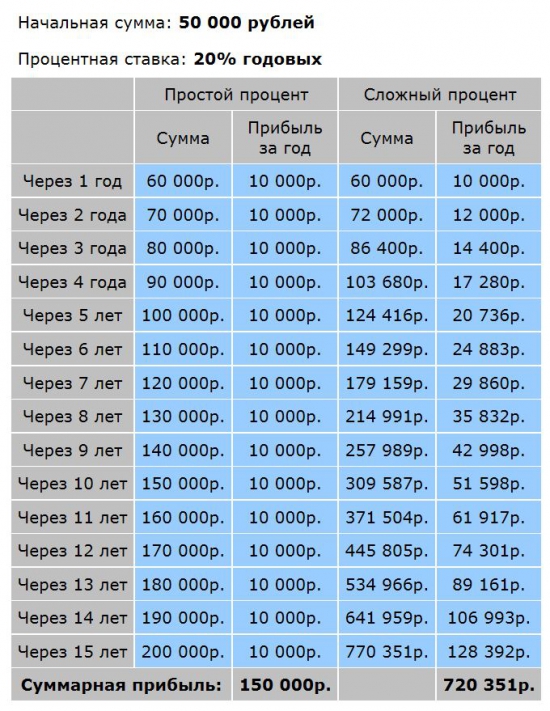  |
Комментарии, как говорится, излишни. Вложения с использованием сложного процента НА ПОРЯДОК выгоднее, чем с простым процентом. Чем больше проценты прибыли, чем дольше срок инвестирования, тем ярче проявляет себя сложный процент.
В случае простого процента график увеличения капитала получается линейный, поскольку вы снимаете прибыль и не даёте ей работать и приносить новую прибыль. В случае сложного процента график получается экспоненциальным, с течением времени кривая увеличения капитала становится всё круче, всё больше стремится вверх. Это происходит оттого, что из года в год прибыль накапливается и создаёт новую прибыль.
На графике ниже показано как вырастет капитал, если вложить 50 000 руб на 15 лет под 10%, 15% и 20%.
 |
Как видите, на длительном промежутке времени очень важным становится то, под какой процент вы инвестируете деньги.
Через 15 лет при 10% годовых 50 тысяч рублей превратятся в 200 тысяч, при 15% — уже в 400 тысяч, а при 20% годовых — в 780 тысяч.
Таким образом, сложный процент является мощным орудием по увеличению капитала на длительных промежутках времени.
Из формулы расчёта сложного процента можно выразить процентную ставку и количество лет (месяцев).
Процентная ставка:
Расчет сложных процентов: Пример 4.
Какая процентная ставка должна быть, чтобы за 10 лет 50 000 рублей превратились в 100 000 рублей?
% = (100000 / 50000) 1/10 — 1 = 0,0718 = 7,18 % годовых
Количество периодов (месяцев, лет):
n = log(1+0,4) (1000000 / 50000) = 8,9 лет










