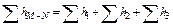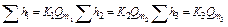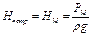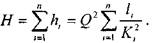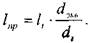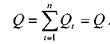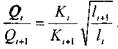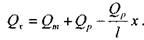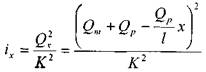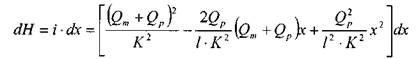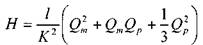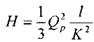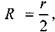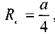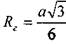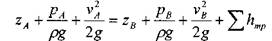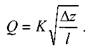Что такое сложные трубопроводы

Простые и сложные трубопроводы

В гидравлике различают простые и сложные трубопроводы. Простым называется такой трубопровод, который служит для подачи жидкости из одного резервуара в другой без ответвлений. Простой трубопровод может иметь по всей длине одинаковое сечение, а может состоять из ряда последовательно соединенных труб различного сечения.

Сложными называются трубопроводы, имеющие ответвления или состоящие из нескольких линий. Их расчет значительно сложнее, чем простых. Однако, некоторые задачи, относящиеся к сложным трубопроводам, можно решать, рассматривая отдельные их элементы, как простые.

Расход жидкости может производиться в какой-либо определенной точке трубопровода, например, на его конце. Такой расход называется транзитным. В некоторых трубопроводах, например, в водопроводах, расход жидкости производится во многих точках по длине. В этих случаях расход называется путевым.

В зависимости от характера сопротивлений трубопроводы подразделяют на длинные и короткие. В длинных трубопроводах потери напора по длине во много раз больше потерь от местных сопротивлений, которые составляют 2—5% от общих потерь энергии в трубопроводе.

В так называемых коротких трубопроводах потери напора от местных сопротивлений велики по сравнению с потерями по длине трубопровода. Принятая классификация позволяет в значительной степени упростить гидравлический расчет трубопроводов.

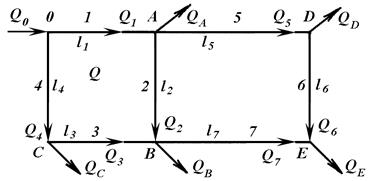
С учетом указанных условий приведены методики расчета напорных, т. е. заполненных по всему сечению трубопроводов, при установившемся равномерном движении жидкости.

Местные гидравлические сопротивления

В производственной практике перемещение жидкости в потоках связано с преодолением сопротивлений по длине потоков, а также и различных местных сопротивлений: поворотов, диафрагм, задвижек, вентилей, кранов, различных ответвлений и т. п.

На преодоление местных сопротивлений затрачивается определенная часть энергии потока, которую часто называют потерей напора на местные сопротивления. Обычно эти потери выражают в долях скоростного напора, соответствующего средней скорости жидкости в трубопроводе до или после местного сопротивления.

Данные о значении коэффициентов различных местных сопротивлений приводятся в соответствующих справочниках, учебниках и различных пособиях по гидравлике в виде отдельных значений, таблиц, эмпирических формул, диаграмм и т. п.

Потери напора при внезапном расширении струи. Теорема Борда.

Исследования потерь энергии (напора), обусловленных различными местными сопротивлениями, ведутся уже более ста лет. В результате экспериментальных исследований, проведенных у нас и за рубежом в различное время, получено огромное количество данных, относящихся к разнообразнейшим местным сопротивлениям для конкретных практических задач.

Что же касается теоретических исследований, то им пока поддаются только некоторые местные сопротивления.

Наиболее полно теоретически исследованы характеристики сопротивлений при внезапном расширении струи.

Общие потери напора

Определение величины потерь по формуле вносит в расчет погрешность тем большую, чем ближе друг от друга расположены отдельные местные сопротивления и чем большие возмущения в жидкости вызываются ими. Это объясняется тем, что величины коэффициентов местных сопротивлений, получаемые из опыта, относятся к условиям стабилизированного потока с обеих сторон каждого из местных сопротивлений, т. е. к условиям, когда до и после каждого из местных сопротивлений имеется достаточно длинный прямой участок трубопровода.

В практике часто встречается, когда местные сопротивления находятся на недостаточно большом удалении друг от друга или расположены даже непосредственно друг за другом. В этих случаях стабилизация потока не происходит и наблюдается взаимное влияние местных сопротивлений.

В результате проведенных исследований установлено, что суммарный коэффициент сопротивления двух или нескольких местных сопротивлений, взаимно влияющих друг на друга, всегда меньше суммы коэффициентов, относящихся к отдельно рассматриваемым местным сопротивлениям.

Поэтому, если вести расчет потерь напора, пренебрегая взаимным влиянием местных сопротивлений, и пользоваться величинами коэффициентов, указанными в справочниках, то результат расчета по формуле дает заведомо завышенные значения потерь напора. В связи с этим на практике при отсутствии данных о взаимном влиянии коэффициенты местных сопротивлений принимаются, как обычно, по справочным данным, т. е. с некоторым запасом.

Для того чтобы взаимным влиянием местных сопротивлений можно было пренебречь, необходимо выбирать расстояние между точками установки этих сопротивлений из определенных условий.

Источник

Сложные трубопроводы

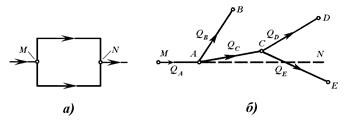
Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их соединением (рис. 3.38, а) или с разветвлениями (рис. 3.38, б).

Рис. 3.38. Схемы сложных трубопроводов

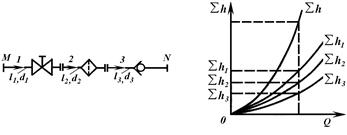
Последовательное соединение. Возьмем несколько труб различной длины, разного диаметра и содержащих разные местные сопротивления, и соединим их последовательно (рис. 3.39, а).

Рис. 3.39. Последовательное соединение трубопроводов

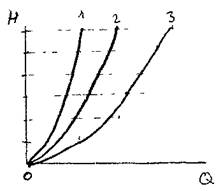
При подаче жидкости по такому составному трубопроводу от точки М к точке N расход жидкости Q во всех последовательно соединенных трубах 1, 2 и 3 будет одинаков, а полная потеря напора между точками М и N равна сумме потерь напора во всех последовательно соединенных трубах. Таким образом, для последовательного соединения имеем следующие основные уравнения:

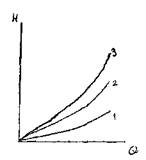
Эти уравнения определяют правила построения характеристик последовательного соединения труб (рис. 3.39, б, стр. 139). Если известны характеристики каждого трубопровода, то по ним можно построить характеристику всего последовательного соединения M-N. Для этого нужно сложить ординаты всех трех кривых.

Параллельное соединение. Такое соединение показано на рис. 3.40, а. трубопроводы 1, 2 и 3 расположены горизонтально.

Рис. 3.40. Параллельное соединение трубопроводов

Очевидно, что расход жидкости в основной магистрали

Выразим потери напора в каждом из трубопроводов через полные напоры в точках М и N :

Отсюда делаем вывод, что

т.е. потери напора в параллельных трубопроводах равны между собой. Их можно выразить в общем виде через соответствующие расходы следующим образом

Из двух последних уравнений вытекает следующее правило: для построения характеристики параллельного соединения нескольких трубопроводов следует сложить абсциссы (расходы) характеристик этих трубопроводов при одинаковых ординатах ( Σ h). Пример такого построения дан на рис. 3.41, б.

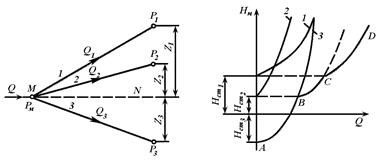
Рис. 3.41. Разветвленный трубопровод

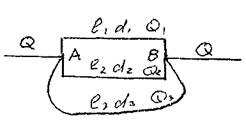
Пусть основной трубопровод имеет разветвление в сечении М-М, от которого отходят, например, три трубы 1, 2 и 3 разных диаметров, содержащие различные местные сопротивления (рис. 3.41, а). Геометрические высоты z₁, z₂ и z₃ конечных сечений и давления P₁, P₂ и P₃ в них будут также различны.

Так же как и для параллельных трубопроводов, общий расход в основном трубопроводе будет равен сумме расходов в каждом трубопроводе:

Записав уравнение Бернулли для сечения М-М и конечного сечения, например первого трубопровода, получим (пренебрегая разностью скоростных высот)

Обозначив сумму первых двух членов через H_ст и выражая третий член через расход, получаем

Аналогично для двух других трубопроводов можно записать

Таким образом, получаем систему четырех уравнений с четырьмя неизвестными: Q₁, Q₂ и Q₃ и H_M.

Для этого случая возможны два вида задач:

Задача 1. Дан расход Q в основной магистрали M_A. Необходимо определить расходы Q_B и Q_D и Q_E, а также потребный напор в точке М.

Задача 2. Дан напор в точке М. Определить расход в магистрали Q и расходы в каждой ветви.

Обе задачи решают на основе одной и той же системы уравнений, число которых на единицу больше числа конечных ветвей, а именно:

уравнение равенства потребных напоров для ветвей CD и CE

уравнение равенства потребных напоров для ветви АВ и сложного трубопровода АСЕD

выражение для потребного напора в точке М

Расчет сложных трубопроводов часто выполняют графоаналитическим способом, т.е. с применением кривых потребного напора и характеристик трубопроводов. Кривую потребного напора для сложного трубопровода следует строить следующим образом: 1) сложный трубопровод разбивают на ряд простых; 2) строят кривые потребных напоров для каждого из простых трубопроводов; 3) складывают кривые потребных напоров для ветвей (и параллельных линий, если они имеются) по правилу сложения характеристик параллельных трубопроводов; 4) полученную кривую складывают с характеристикой последовательно присоединенного трубопровода по соответствующему правилу.

Таким образом, при расчете идут от конечных точек трубопровода к начальной точке, т.е. против течения жидкости.

Сложный кольцевой трубопровод. Представляет собой систему смежных замкнутых контуров, с отбором жидкости в узловых точках или с непрерывной раздачей жидкости на отдельных участках (рис. 3.42).

Рис. 3.42. Схема сложного кольцевого трубопровода

Для расчета таких трубопроводов типичной является следующая задача. Дан максимальный напор в начальной точке, т.е. в точке 0, минимальный напор в наиболее удаленной точке Е, расходы во всех шести узлах и длины семи участков. Требуется определить диаметры трубопроводов на всех участках.

Источник

СЛОЖНЫЙ ТРУБОПРОВОД

К сложным трубопроводам следует относить те трубопроводы, которые не подходят к категории простых трубопроводов, т.е к сложным трубопроводам следует отнести:

трубопроводы, собранные из труб разного диаметра (последовательное соедине­ние трубопроводов),

трубопроводы, имеющие разветвления: параллельное соединение трубопроводов, сети трубопроводов, трубопроводы с непрерывной раздачей жидкости.

Последовательное соединение трубопроводов. При последовательном соединении

трубопроводов конец предыдущего просто­го трубопровода одновременно является началом следующего простого трубопрово­да. В сложном трубопроводе, состоящем из последовательно соединённых простых 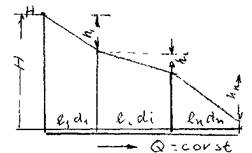трубопроводов, последние в литературе на­зываются участками этого трубопровода. Расход жидкости во всех участках сложного трубопровода остаётся одинаковым Q = const. Общие потери напора во всём трубопрово­де будут равны сумме потерь напора во всех отдельных его участках.

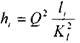
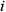
где — потери напора на — том участке трубопровода.

Таким образом, потери напора в трубопроводе, состоящем из последовательно со­единённых друг с другом участков равны квадрату расхода жидкости в трубопроводе ум­ноженному на сумму удельных сопротивлений всех участков.

Сложный трубопровод, состоящий из последовательно соединённых простых трубо­проводов можно свести к простому трубопроводу с одинаковым (эквивалентным) диамет­ром, при этом длины участков будут пересчитываться, чтобы сохранить реальные гидрав­лические сопротивления участков трубопровода.

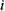
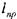
Так приведённая длина — того участка будет:

Следует отметить, что величина скоростного напора также зависит от диаметра трубопровода, и при определении приведённой длины участка мы вносим некоторую ошибку, которая будет тем большей, чем больше разница в величинах фактического и эк­вивалентного диаметров. В таких случаях можно рекомендовать другой, более сложный способ.

Параллельное соединение трубопроводов. Схема прокладки параллельных трубо­проводов используется в тех случаях, когда на трассе магистрального трубопровода есть участки, где требуется уменьшить гидрав­лические сопротивления трубопровода (вы­сокие перевальные точки трубопровода) или при заложении трубопровода в трудно­ доступных местах (переход через реки и др.). При параллельном соединении трубо­проводов имеются две особые точки, называемые точками разветвления.

В этих точках находятся концы параллельных ветвей трубопровода (точки А и В). Будем считать, что жидкость движется слева направо, тогда общий для всех ветвей напор в точке А будет больше напора в другой общей для всех ветвей трубопровода точке В (НА Н к ). В точке А поток жидкости растекается по параллельным ветвям, а в точке В вновь собирается в еди­ный трубопровод. Каждая ветвь может иметь различные геометрические размеры: диа­метр и протяжённость (длину). Поскольку вся система трубопроводов является закрытой, то поток жидкости в данной системе будет транзитным, т.е.

Жидкость движется по всем ветвям при одинаковой разности напоров:

> тогда расход жидкости по каждой ветви можно записать в виде:

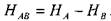
Поскольку ветвей в системе п,, а число неизвестных в системе уравнений будет п+1, включая напор, затрачиваемый на прохождение жидкости по всем ветвям 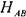, то в каче­стве дополнительного уравнения в системе будет использовано уравнение неразрывности:

При решении системы уравнений можно воспользоваться соотношением:

Для построения гидравлической характери­стики системы параллельных трубопроводов можно воспользоваться методом графического суммирования. Суммирование осуществляется по оси расходов Q. т.к.

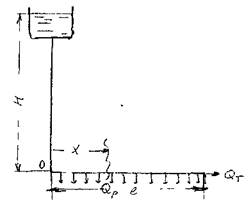
Трубопроводы с непрерывным (распределённым расходом). В данном случае пред­полагается, что вдоль всей длины трубопровода располагаются одинаковые равномерно

раз­

даётся по всей длине трубопровода.

Тогда в некотором сечении трубопровода на расстоянии х от его начала расход будет равен:

Тогда гидравлический уклон в сечении х на малом отрезке dx:

Уравнение падения напора вдоль элемента dx запишется следующим образом:

После интегрирования от 0 до / получим:

и при :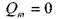

Сети трубопроводов. Если магистральные трубопроводы принято рассматривать как сред­ства внешнего транспорта жидкостей и газов, то сети используются в качестве оборудования для внутреннего транспорта жидких или газообраз­ных продуктов. По направлению движения жидкости (газа) сети различают на сборные и раздаточные (распределительные). В сборных сетях имеется группа источников возникновения ­

где воздух подаётся в служебные помещения или на рабочие места. К такому же типу се­тей можно отнести систему теплоснабжения и др. Сети строятся в населённых пунктах, на предприятиях, отдельных территориях. Трубы в таких системах могут изготавливаться из различных материалов в зависимости от технологических требований, предъявляемых к сетям. В сборных сетях источники жидкости и газа располагают напором, обеспечиваю­щим движение жидкости (газа) до магистралей. Если напоры недостаточны, то создаются специальные, узлы, где напор обеспечивается принудительным образом. Имеется, по крайней мере, две группы задач для гидравлического расчёта сетей: проектирование но­вых сетей и расчёт пропускной способности существующих сетей. Принципы расчёта по­хожи. В основе расчётных формул положены уравнения Дарси-Вейсбаха и Шези. Предва­рительно в сети выбирается ветвь с наибольшей нагрузкой (расход и напор). Эта ветвь рассматривается как своеобразный трубопровод, который, в общем случае можно отнести к категории последовательного соединения простых трубопроводов. Другие участки рас-

считываются самостоятельно. После завершения расчётных работ, осуществляется про­верка соответствия результатов расчётов в узлах сети. После анализа расхождений резуль­татов решений в узлах сети осуществляется корректировка исходных данных. Таким обра­зом, метод итераций является наиболее приемлемым для расчёта сетей.

Трубопроводы некруглого профиля. Подавляющее большинство трубопроводов со­бирается из круглых труб. Преимущество круглого сечения очевидны: круглое сечение обладает максимальной пропускной способностью и минимальным гидравлическим со­противлением. Так гидравлический радиус для круглого сечения:

для треугольного сечения для квадратного сечения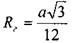

для шестиугольного сечения

Тем не менее, трубы некруглого сечения применяются в промышленности там, где потери напора не играют особой роли. Это, в первую очередь, воздуховоды с малыми ско­ростями движения воздуха, и т.д.

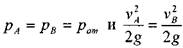
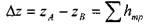
Поскольку: , то:

?

Источник

Классификация трубопроводов

Все многообразие трубопроводов делят условно на короткие и длинные простые и сложные.

Короткие и длинные трубопроводы

В коротком трубопроводе потери удельной механической энергии на местных сопротивлениях и по длине соизмеримы.

В длинных трубопроводах потери на местных сопротивлениях малы по сравнению с потерями по длине. При расчете длинных трубопроводов потери в местных сопротивлениях учитывают завышая потери по длине на 5-10%.

Простые и сложные трубопроводы

Простым трубопроводом называют такой, которые не содержит ответвлений и разветвлений и собран из труб одного диаметра. Во всех остальных случаях трубопровод называют сложным.

Получается, что сложным называют трубопровод, состоящий из труб разного диаметра, включающий ответвления.

Различают последовательное и параллельное соединение участков в сложных трубопроводах.

Последовательное соединение

Пример последовательного соединения показан на рисунке.

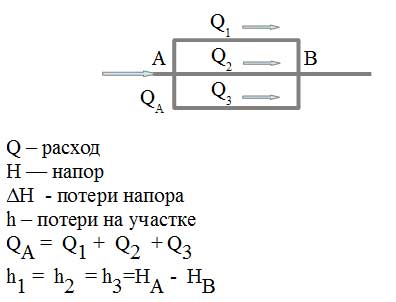
Такой трубопровод состоит из участков, включенных последовательно друг другу. При отсутствии утечек расход жидкости в каждом из на всем протяжении трубопровода будет постоянен и одинаков.

Параллельное соединение участков

Пример параллельного соединения показан на рисунке.

При параллельном соединении труд расход между ними распределяется таким образом, чтобы потери напора на каждом участке были одинаковы и равнялись концевой разности напора.

Источник