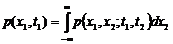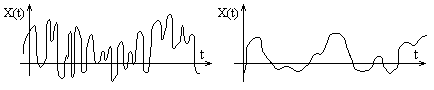Что такое случайная функция

Понятие о случайной функции.

СЕВАСТОПОЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

М.М. Гхашим, Т.В.Чернэуцану

СЛУЧАЙНЫЕ ФУНКЦИИ

ученым советом института

Гхашим М.М., Т.В.Чернэуцану

Случайные функции: учеб.-метод. пособие. – Севастополь: СевГУ, 2015.

В данном пособии рассмотрены три основных раздела: « », « », « ». Каждый из разделов включает в себя основные вопросы теории, разбор типовых примеров, задания для самостоятельной работы с ответами к ним.

предназначено для студентов третьего курса при изучении темы « ».

© Издание СевГУ, 2015

ОГЛАВЛЕНИЕ

§ 1. Понятие о случайной функции……………………………………

§ 2. Характеристики случайных функций……………………………

§ 3. Оператор динамической системы……………………………….

§ 4. Линейные преобразования случайных функций………………

§ 5. Стационарные случайные процессы……………………

§ 6. Спектральное разложение стационарной случайной функции………

§ 7. Эргодическое свойство стационарных случайных функций………….

Решение типовых задач………………………………………………..

Задачи для самостоятельного решения………………………………

Случайные функции

Понятие о случайной функции.

В курсе теории вероятностей основным предметом исследования были случайные величины, которые характеризовались тем, что в результате опыта принимали некоторое одно, заранее неизвестное, но единственное значение. Т.е., случайные явления изучались как бы в «статике», в каких-то фиксированных постоянных условиях отдельного опыта. Однако на практике часто приходится иметь дело со случайными величинами, непрерывно изменяющимися в процессе опыта. Например, угол упреждения при непрерывном прицеливании по движущейся цели; отклонение траектории управляемого снаряда от теоретической в процессе управления или самонаведения, и т.д. В принципе, любые системы с автоматизированным управлением предъявляют определенные требования к соответствующей теоретической базе – теории автоматического управления. Развитие этой теории невозможно без анализа ошибок, неизбежно сопровождающих процессы управления, которые всегда протекают в условиях непрерывно действующих случайных возмущений или «помех». Эти возмущения по своей природе являются случайными функциями. Итак:

Определение. Случайной функцией X(t) называют функцию неслучайного аргумента t, которая при каждом фиксированном значении аргумента является случайной величиной.

Конкретный вид, принимаемый случайной функцией X(t) в результате опыта, называется реализацией случайной функции.

Пример. Самолет на воздушном курсе имеет теоретически постоянную воздушную скорость V. Фактически его скорость колеблется около этого среднего номинального значения и представляет собой случайную функцию времени. Полет можно рассматривать как опыт, в котором случайная функция V(t) принимает определенную реализацию (Рис.1).

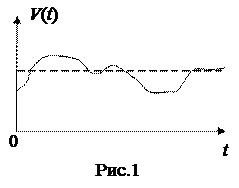От опыта к опыту вид реализации меняется. Если на самолете установлен самописец, то он в каждом полете запишет новую, отличную от других, реализацию случайной функции. В результате нескольких полетов можно получить семейство реализаций случайной функции V(t) (Рис.2).

На практике встречаются случайные функции, зависящие не от одного аргумента, а от нескольких, например, состояние атмосферы (температура, давление, ветер, осадки). В данном курсе мы будем рассматривать только случайные функции одного аргумента. Так как этим аргументом чаще всего является время, будем обозначать его буквой t. Кроме того, условимся обозначать случайные функции большими буквами (X(t), Y(t), …) в отличие от неслучайных функций (x(t), y(t), …).

Рассмотрим некоторую случайную функцию X(t). Предположим, что над ней произведено n независимых опытов, в результате которых получено n реализаций, которые мы обозначим соответственно номерам опытов x₁(t), x₂(t), …, x_n(t). Очевидно, каждая реализация есть обычная (не случайная) функция. Таким образом, в результате каждого опыта случайная функция X(t) превращается в не случайную функцию.

Зафиксируем теперь некоторое значение аргумента t. В этом случае случайная функция X(t) превратится в случайную величину.

Определение. Сечением случайной функции X(t) называют случайную величину, соответствующую фиксированному значению аргумента случайной функции.

Мы видим, что случайная функция совмещает в себе черты случайной величины и функции. В дальнейшем часто будем попеременно рассматривать одну и ту же функцию X(t) то как случайную функцию, то как случайную величину, в зависимости от того, рассматривается ли она на всем диапазоне изменения t или при его фиксированном значении.

Рассмотрим случайную величину X(t) – сечение случайной функции в момент t. Эта случайная величина, очевидно, обладает законом распределения, который в общем случае зависит от t. Обозначим его f(x, t). Функция f(x, t) называется одномерным законом распределения случайной функции X(t).

Очевидно, функция f(x, t) не является полной, исчерпывающей характеристикой случайной функции X(t), т.к. она характеризует только закон распределения X(t) для данного, хотя и произвольного t и не отвечает на вопрос о зависимости случайных величин X(t) при различных t. С этой точки зрения более полной характеристикой случайной функции X(t) является так называемый двумерный закон распределения: f(x₁, x₂; t₁, t₂). Это – закон распределения системы двух случайных величин X(t₁), X(t₂), т.е. двух произвольных сечений случайной функции X(t). Но и эта характеристика в общем случае не является исчерпывающей. Очевидно, теоретически можно неограниченно увеличивать число аргументов и получать все более полную характеристику случайной функции, но оперировать столь громоздкими характеристиками, зависящими от многих аргументов, крайне затруднительно. В пределах данного курса мы вообще не будем пользоваться законами распределения, а ограничимся рассмотрением простейших характеристик случайных функций, аналогичных числовым характеристикам случайных величин.

Источник

Случайная функция

Полезное

Смотреть что такое «Случайная функция» в других словарях:

СЛУЧАЙНАЯ ФУНКЦИЯ — функция произвольного аргумента такая, что ее значения определяются случайным исходом некоторого испытания, причем для них существует определенное распределение вероятностей. Понятие случайной функции весьма близко понятию случайного процесса … Большой Энциклопедический словарь

СЛУЧАЙНАЯ ФУНКЦИЯ — функция 2 х аргументов X(t) = X(ω,t); множество элементарных событий, произвольное множество. Если в вещественное множество и параметр t интерпретировать как время, то X(t) называется случайным процессом. Аппарат С. ф. широко используется… … Геологическая энциклопедия

Случайная функция — [ran­dom function] “функция X(t) произвольного аргумента (t), t ∈ T, значения которой при любом t являются случайной величиной с определенным распределением вероятностей” (МЭС, стр. 547). Если t принимает числовые значения, которые… … Экономико-математический словарь

случайная функция — функция произвольного аргумента, такая, что её значения определяются случайным исходом некоторого испытания, причём для них существует определенное распределение вероятностей. Понятие случайной функции весьма близко понятию случайного процесса. * … Энциклопедический словарь

случайная функция — atsitiktinė funkcija statusas T sritis automatika atitikmenys: angl. random function vok. Zufallsfunktion, f rus. случайная функция, f pranc. fonction aléatoire, f … Automatikos terminų žodynas

СЛУЧАЙНАЯ ФУНКЦИЯ — функция произвольного аргумента t(заданная на множестве Тего значений и принимающая числовые значения или, более общо, значения из какого то векторного пространства) такая, что ее значения определяются с помощью нек ро го испытания и в… … Математическая энциклопедия

СЛУЧАЙНАЯ ФУНКЦИЯ — функция произвольного аргумента, такая, что её значения определяются случайным исходом нек рого испытания, причём для них существует определ. распределение вероятностей. Понятие С. ф. весьма близко понятию случайного процесса … Естествознание. Энциклопедический словарь

Случайная функция — … Википедия

Источник

Случайные функции. Характеристики случайных функций

Случайная функция – функция, которая в результате опыта может принять тот или иной неизвестный заранее конкретный вид. Обычно аргументом случайной функции (с.ф.) является время, тогда с.ф. называют случайным процессом (с.п.).

С.ф. непрерывно изменяющегося аргумента t называется такая с.в., распределение которой зависит не только от аргумента t=t1, но и от того, какие частные значения принимала эта величина при других значениях данного аргумента t=t2. Эти с.в. корреляционно связаны между собой и тем больше, чем ближе одни к другим значения аргументов. В пределе при интервале между двумя значениями аргумента, стремящемся к нулю, коэффициент корреляции равен единице:

,

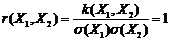
т.е. t1 и t1+Dt1 при Dt1®0 связаны линейной зависимостью.

С.ф. принимает в результате одного опыта бесчисленное (в общем случае несчетное) множество значений – по одному для каждого значения аргумента или для каждой совокупности значений аргументов. Эта функция имеет одно вполне определенное значение для каждого момента времени. Результат измерения непрерывно изменяющейся величины является такой с.в., которая в каждом данном опыте представляет собой определенную функцию времени.

С.ф. можно также рассматривать как бесконечную совокупность с.в., зависящую от одного или нескольких непрерывно изменяющихся параметров t. Каждому данному значению параметра t соответствует одна с.в Xt. Вместе все с.в. Xt определяют с.ф. X(t). Эти с.в. корреляционно связаны между собой и тем сильнее, чем ближе друг к другу.

Элементарная с.ф. – это произведение обычной с.в. Х на некоторую неслучайную функцию j(t): X(t)=X×j(t), т.е. такая с.ф., у которой случайным является не вид, а только ее масштаб.

С.ф. 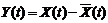— имеет м.о. равное нулю. p – плотность распределения с.в. Х (значения с.ф. X(t)), взятой при произвольном значении t1 аргумента t.

Реализация с.ф. X(t) – описывается уравнением x=f1(t) при t=t1 и уравнением x=f2(t) при t=t2.

Вообще функции x=f1(t) и x=f2(t) – различные функции. Но эти функции тождественны и линейны тем более, чем более (t1®t2) t1 ближе к t2.

Одномерная плотность вероятности с.ф. p(x,t) – зависит от х и от параметра t. Двумерная плотность вероятности p(x1,x2;t1,t2) – совместный закон распределения значений X(t1) и X(t2) с. ф. X(t) при двух произвольных значениях t и t¢ аргумента t.

. (66.5)

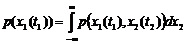
В общем случае функция X(t) характеризуется большим числом n-мерных законов распределения .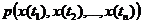

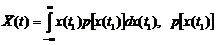
— функция, зависящая от x и t.

Степень зависимости с.в. для различных значений аргумента характеризуется автокорреляционной функцией.

(67.5)=(34.3),

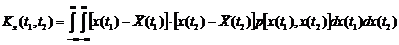
где 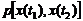— совместная плотность распределения двух с.в. (значений с.ф.), взятых при двух произвольных значениях t1 и t2 аргумента t. При t1=t2=t получаем дисперсию D(t).

Рис. Корреляционно связанные случайные функции

Если две с.ф. X(t) и Y(t), образующие систему не являются независимыми, то тождественно не равна нулю их взаимная корреляционная функция:

(68.5),

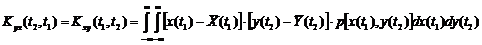
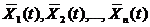
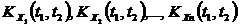
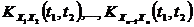
Если X(t) и Y(t) независимы, то KXY(t1,t2)=0. Система из n с.ф. X1(t), X2(t). Xn(t) характеризуется n м.о. , n автокорреляционными функциями и еще n(n-1)/2 корреляционными функциями .

Особое значение имеют стационарные случайные функции, вероятностные характеристики которых не меняются при любом сдвиге аргумента. М.о. стационарной с.ф. постоянно (т.е. не является функцией), а корреляционная функция зависит лишь от разности значений аргументов ti и tj.

, (69.5)

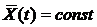
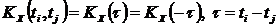
Это четная функция (симметрично OY).

Из (69.5)® .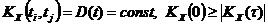

При большом значении интервала времени t=t2-t1 отклонение ординаты с.ф. от ее м.о. в момент времени t2 становится практически независимым от значения этого отклонения в момент времени t1. В этом случае функция KX(t), дающая значение корреляционного момента между X(t1) и X(t2), при ½t½®¥ стремится к нулю.

Многие стационарные с.ф. обладают эргодическим свойством, которое заключается в том, что при неограниченно возрастающем интервале наблюдения среднее наблюденное значение стационарной с.ф. с вероятностью, равной 1, будет неограниченно приближаться к ее м.о. Наблюдение стационарной с.ф. при разных значениях t на достаточно большом интервале в одном опыте равноценно наблюдению ее значений при одном и том же значении t в ряде опытов.

Иногда требуется определить характеристики преобразованных с.ф. по характеристикам исходных с.ф. Так если

(70.5),

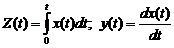
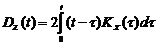
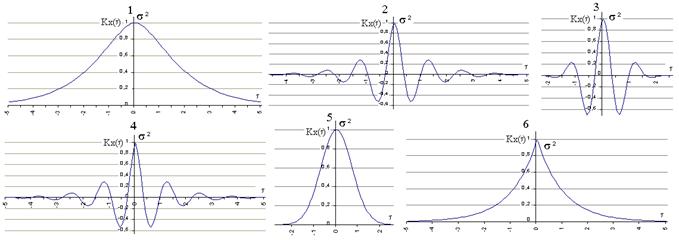
При интегрировании или дифференцировании с.ф. получаем также с.ф. Если X(t) распределена нормально, то Z(t) и Y(t) распределены тоже нормально. Если X(t) – стационарная с.ф., то Z(t) уже не стационарная с.ф., т.к. зависит от t.

Примеры корреляционных функций.

1) (из (2) при b®0); 2) ;

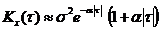
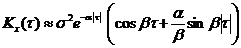
3) ; 4) ;

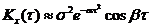
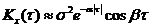
5) (из (3) при b®0); 6) (из (4) при b®0).

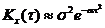
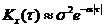
На графиках a = 1, b = 5, s = 1.

Корреляционные функции 4 и 6 – не имеют производных при t=0. Соответствующие спектральные плотности:

2) ;

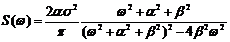
3) ;

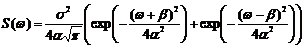
4) ;

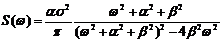
6) .

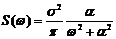
Чтобы найти корреляционную функцию интеграла (производной) от с.ф., нужно дважды проинтегрировать (продифференцировать) корреляционную функцию исходной с.ф. сначала по одному, затем по другому аргументу:

(71.5).

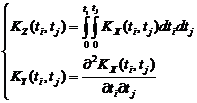
Формула (71) для стационарной функции примет вид:

.

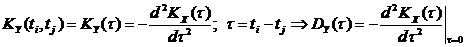
Корреляционная функция с.ф. и ее производной 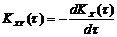. Для дифференцируемого стационарного процесса ордината с.ф. и ее производной, взятая в тот же момент времени являются некоррелированными с.в. (а для нормального процесса и независимыми).

При умножении с.ф. на детерминированную получаем с.ф. Z(t)=a(t)X(t), корреляционная функция которой равна

Сумма двух с.ф. является тоже с.ф. Z(t)=X(t)+Y(t) и ее корреляционная функция при наличии корреляционной связи между X(t) и Y(t):

Если X(t) и Y(t) независимы, то KXY(t1,t2)=0. М.о. с.ф. Z(t): .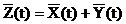

Поможем написать любую работу на аналогичную тему

Случайные функции. Характеристики случайных функций

Случайные функции. Характеристики случайных функций

Случайные функции. Характеристики случайных функций

Источник

Определение случайной функции

Определение 1.1.Случайной функцией называют функцию неслучайного аргумента t, которая при каждом фиксированием значении аргумента является случайной величиной. Случайные функции аргумента t обозначают прописными буквами X (t), Y(t) и т. д.

Определение 1.2. Сечением случайной функции называют случайную величину, соответствующую фиксированному значению аргумента случайной функции. Например, для случайной функции X(t) = t 2 U, приведенной выше, при значениях, аргумента t 2 = 2 и t₂ = 1,5 были получены соответственно случайные величины Х₁= 4U и X₂ = 2,25 U, которые и являются сечениями заданной случайной функции.

Итак, случайную функцию можно рассматривать как совокупность случайных величин , зависящих от параметра t. Возможно и другое истолкование случайной функции, если ввести понятие ее реализации.

Определение 1.3. Реализацией (траекторией, выборочной функцией) случайной функции X (t) называют неслучайную функцию аргумента t, равной которой может оказаться случайная функция в результате испытания.

Таким образом, если в опыте наблюдают случайную функцию, то в действительности наблюдают одну из возможных ее реализаций; очевидно, при повторении опыта будет наблюдаться другая реализация.

Итак, случайную функцию можно рассматривать как совокупность ее воз­можных реализаций.

Определение 1.4. Случайным (стохастическим) процессом называют случайную функцию аргумента t, который истолковывается как время.

Заметим, что если аргумент случайной функции изменяется дискретно, то соответствующие ему значения случайной функции (случайные величины) образуют случайную последовательность.

Определение 1.5. Случайный процесс X(t) называется процессом с дискретным временем, если система, в которой он протекает, может менять свои состояния только в моменты t₁, t₂. t_i . число которых конечно или счетно. Множество T является дискретным.

Определение 1.6. Случайный процесс X(t) называется процессом с непрерывным временем, если переходы системы из состояния в состояние могут происходить в любой момент t наблюдаемого периода t.

Определение 1.7. Одномерный случайный процесс X(t) называется процессом с непрерывными состояниями, если его сечение в любой момент t представляет собой не дискретную, а непрерывную (или смешанную) случайную величину и, значит, множество ее значений X (кси) несчетно. Аналогично, многомерный (векторный) случайный процесс называется процессом с непрерывными состояниями, если при любом t множество возможных значений случайного вектора, определяющего состояние системы S, в которой протекает процесс, несчетно. Примеры случайных процессов с непрерывными состояниями: 1) напряжение U(t) питания ЭВМ в момент t; 2) давление газа P(t) в заданном резервуаре в момент t; 3) координаты частицы, совершающей броуновское движение X(t), Y(t), в момент t (двумерный случайный процесс с непрерывными состояниями); 4) параметры, характеризующие в момент t состояние космической ракеты, выводимой на орбиту (многомерный случайный процесс с непрерывными состояниями).

Таким образом, в зависимости от характера множества Т значений аргумента t, в которые возможны переходы системы из состояния в состояние, а также множества X самих состояний все случайные процессы можно разделить на четыре класса:

1а. Процессы с дискретными состояниями и дискретным временем.

16. Процессы с дискретными состояниями и непрерывным временем.

2а. Процессы с непрерывными состояниями и дискретным временем.

26. Процессы с непрерывными состояниями и непрерывным временем.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник