Что такое случайная величина и как соотносятся теоретические вероятности и эмпирические частоты

Случайные величины и распределения вероятностей как основные объекты изучения математической статистики и эмпирической социологии

Основными объектами изучения для математической статистики являются т. н. случайные величины (пока – одномерные). Это функции, определенные на некоторых случайных событиях («случайное событие» – основное понятие теории вероятностей; как известно, сам термин «вероятность» осмыслен лишь применительно к некоторому случайному событию) и принимающие числовые значения. В качестве типичного для социолога случайного события является выбор того или иного респондента. Случайными величинами могут служить признаки, определенные для этих респондентов.

Сказанным не ограничивается определение случайной величины. Мы не упомянули самого главного – для каждой совокупности значений случайной величины должна быть определена вероятность того, что, обследуя респондентов, социолог встретит значение из этой совокупности.

Напомним, что вероятностью события называют некоторую числовую характеристику степени возможности его появления в определенных, могущих повторяться неограниченное число раз, условиях. Выше в качестве события указывался выбор респондента. О вероятности этого события говорить не будем (поскольку такая вероятность связана с правилами построения выборки, которые мы не затрагиваем). В интересующем нас случае тот факт, что случайная величина приобретает некоторое значение, сам рассматривается как случайное событие. И именно задание соответствующих вероятностей сопрягается с определением случайной величины. Условия же реализации нашего случайного события – это условия, определяющие отбор респондента.

Совокупность вероятностей встречаемости значений рассматриваемой случайной величины называется отвечающим ей распределением вероятностей, или просто ее распределением. Функция, задающая для определенных наборов значений случайной величины отвечающую им вероятность, называется функцией распределения этой случайной величины. Задать случайную величину, по существу, и означает задать соответствующее вероятностное распределение.

Чтобы было возможно использование аппарата математической статистики, необходимо частотные выборочные распределения расценивать как выборочные представления генеральных распределений вероятностей. Каждое такое распределение ассоциируется со случайной величиной.

Так, например, для выборки из 10 респондентов, сведения о которой фигурируют в таблице 1, выборочное частотное распределение, отвечающее случайной величине «Удовлетворенность трудом», будет иметь вид, представленный в таблице 2.

Пример частотной таблицы, построенной на основе данных таблицы 1 и отражающей выборочное представление распределения случайной величины «удовлетворенность трудом».

Пример частотной таблицы, построенной на основе данных таблицы 1 и отражающей выборочное представление распределения двумерной случайной величины («пол», «удовлетворенность трудом»).

В разделе 2 второй части понятие частотных таблиц будет обсуждено более подробно.

Итак, поскольку исследователь изначально имеет дело лишь с частотами, а не с соответствующими вероятностями, то фактически исходные случайные величины предстают перед ним в весьма приближенном виде. То, что на основе выборочных данных мы рассчитываем не сами параметры распределений, а лишь их выборочные оценки (отвечающие им статистики), усугубляет степень приблизительности искомых закономерностей. Другими словами, вид закономерности, найденной для выборки, вообще говоря, будет отличаться от вида ее для генеральной совокупности. Естественно, важную роль должна играть оценка подобного различия, поскольку нас, вообще говоря, интересуют закономерности, свойственные генеральной совокупности, хотя на практике мы и имеем дело лишь с выборкой. Именно такую оценку мы и сможем сделать, пользуясь положениями математической статистики.

В решении описанных двух задач по существу и заключается поиск статистических закономерностей. Ясно, что эти задачи весьма актуальны и для социолога. Другими словами, для него является естественным такое же понимание сути искомых соотношений между наблюдаемыми величинами, какое «заложено» в математической статистике. Обоснуем это более подробно.

Должны ли случайные величины интересовать социолога? Конечно. И социолог ими фактически пользуется, не употребляя, правда, соответствующего термина. В своей специфичной ситуации исследователь использует термин «признак» или «совокупность признаков». Обращение социолога к математической статистике по существу начинается со статистической трактовки значений используемых признаков. К примеру, чаще всего, социолога интересует не тот факт, что, скажем, ученик 10 класса средней школы № 5 города N Ваня Иванов намеревается поступить в институт, а более общее явление: например, то, что среди десятиклассников рассматриваемого региона, обладающих определенными социально-демографическими характеристиками (мужчин, горожан и т.д. ), велика доля людей, намеревающихся получить высшее образование. Обобщая сказанное, можно полагать, что социолога интересует распределение долей тех объектов совокупности (десятиклассников изучаемого региона), которые обладают определенными значениями рассматриваемого признака (в нашем примере речь идет о признаке «намерение респондента»), или определенными сочетаниями значений нескольких рассматриваемых признаков (например, трех: пола, местожительства, намерения).

Первым шагом сжатия информации, содержащейся в матрице объект-признак (см. таблицу 1), как правило, является получение частотных распределений разной размерности (см. таблицы 2 и 3). Именно с изучения таких распределений обычно начинается анализ данных.

Таким образом, в качестве случайной величины перед социологом выступает признак (набор признаков), вместо вероятностей значений случайной величины исследователь имеет дело с относительной частотой встречаемости значений признака, вместо вероятностного распределения – с частотным, вместо параметров распределения – с отвечающими им статистиками. Рассчитав интересующие его статистики, он стремится обобщить результаты на генеральную совокупность.

Поясним, что именно мешает применению методов математической статистики в социологических исследованиях. Проведем линию размежевания между математической статистикой и теми лежащими вне ее методами, которые, давая социологу возможность поиска статистических закономерностей, в то же время позволяют преодолеть соответствующие трудности.

Сразу подчеркнем, что эти трудности можно разделить на две большие группы.

Трудности первой группы типичны не только для социологии, но и для многих других наук, имеющих дело с эмпирическими данными и направленных на выявление статистических закономерностей (в числе таких наук могут быть названы биология, геология, медицина, история, психология). Именно потребности таких наук послужили толчком к развитию методов анализа данных как некой замены математико-статистических подходов для тех ситуаций, когда последние оказываются неприменимыми.

Трудности второй группы специфичны именно для социологии. Говоря о них, мы будем иметь в виду не анализ данных вообще, а анализ социологических данных. В следующем параграфе коснемся трудностей первой группы. Социологическая специфика будет затронута в разделе 5.

4. Математическая статистика и анализ данных:

Источник

Случайные события и случайные величины. Основные понятия теории вероятностей. Сбор и регистрация исходных статистических данных.

Случайным событием (или просто событием) называется всякое явление, которое может произойти или не произойти при осуществлении определенной совокупности условий. Теория вероятностей имеет дело с такими событиями, которые имеют массовый характер. Это значит, что данная совокупность условий может быть воспроизведена неограниченное число раз. Каждое такое осуществление данной совокупности условий называют испытанием (или опытом).

Если, например, испытание состоит в бросании монеты, то выпадение герба является событием; если испытание — изготовление подшипника данного типа, то соответствие подшипника стандарту — событие; если испытание — бросание игральной кости, т. е. кубика, на гранях которого проставлены цифры (очки) от 1 до 6, to выпадение пятерки — событие.

Пусть при n испытаниях событие A появилось m раз.

Отношение m/n называется частотой (относительной частотой) события A и обозначается Р*(А)=m/n

Опыт показывает, что при многократном повторении испытаний частота Р*(А) случайного события обладает устойчивостью. Поясним это на примере.

Пусть при бросании монеты 4040 раз герб выпал 2048 раз. Частота появления герба в данной серии опытов равна Р*(А)=m/n=2048/4040=0,5069. При бросании той же монеты 12000 раз герб выпал 6019 раз. Следовательно, в этом случае частота Р*(А)=6019/12000=0,5016. Наконец, при 24000 бросаний герб появился 12012 раз с частотой Р*(А)=0,5005. Таким образом, мы видим, что при большом числе бросаний монеты частота появления герба обладает устойчивостью, т. е. мало отличается от числа 0,5. Как показывает опыт, это отклонение частоты от числа 0,5 уменьшается с увеличением числа испытаний. Наблюдаемое в этом примере свойство устойчивости частоты является общим свойством массовых случайных событий, а именно, всегда существует такое число, к которому приближается частота появления данного события, мало отличаясь от него при большом числе испытаний. Это число называется вероятностью события. Оно выражает объективную возможность появления события. Чем больше вероятность события, тем более возможным оказывается его появление. Вероятность события A будем обозначать через Р(А). В рассмотренном выше примере вероятность появления герба, очевидно, равна 0,5.

Событие называется достоверным, если оно в данном опыте обязательно должно произойти; наоборот, событие называется невозможным, если оно в данном опыте не может произойти.

Пусть, например, из урны, содержащей только черные шары, вынимают шар. Тогда появление черного шара — достоверное событие; появление белого шара — невозможное событие.

Если событие достоверно, то оно произойдет при каждом испытании (m=n). Поэтому частота достоверного события всегда равна единице. Наоборот, если событие невозможно, то оно ни при одном испытании не осуществится (m=0). Следовательно, частота невозможного события в любой серии испытаний равна нулю. Поэтому вероятность достоверного события равна единице, а вероятность невозможного события равна нулю.

Если событие A не является ни достоверным, ни невозможным, то его частота m/n при большом числе испытаний будет мало отличаться от некоторого числа p (где 0

Определение: Случайной называется величина, которая в результате испытания принимает только одно значение из возможного множества своих значение, наперед неизвестное и зависящее от случайных причин.

Различают два вида случайных величин: дискретные и непрерывные.

Определение: Случайная величина Х называется дискретной (прерывной), если множество ее значений конечное или бесконечное, но счетное.

Другими словами, возможные значения дискретной случайной величину можно перенумеровать.

Описать случайную величину можно с помощью ее закона распределения.

Определение: Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и их вероятностями.

Закон распределения дискретной случайной величины Х может быть задан в виде таблицы, в первой строке которой указаны в порядке возрастания все возможные значения случайной величины, а во второй строке соответствующие вероятности этих значений, т.е.

Такая таблица называется рядом распределения дискретной случайной величины.

Если множество возможных значений случайной величины бесконечно, то ряд р₁+ р₂+…+ р_n+… сходится и его сумма равна 1.

Закон распределения дискретной случайной величины Х можно изобразить графически, для чего в прямоугольной системе координат строят ломаную, соединяющую последовательно точки с координатами (x_i;p_i), i=1,2,…n. Полученную линию называют многоугольником распределения (рис.1).

Закон распределения дискретной случайной величины Х может быть также задан аналитически (в виде формулы):

Полное описание случайной величины дает также функция распределения.

Определение: Функцией распределения дискретной случайной величины Хназывается функция F(x), определяющая для каждого значения х вероятность того, что случайная величина Х примет значение, меньше х:

Источник

Критерии согласия. Теоретические и эмпирические частоты

Эмпирические частоты получают в результате опыта (наблюдения). Теоретические частоты рассчитывают по формулам. Для нормального закона распределения их можно найти следующим образом:

где — сумма эмпирических частот; — разность между двумя соседними вариантами; — выборочное среднеквадратическое отклонение; ; — выборочная средняя арифметическая; — см. прил. 1.

Возникает необходимость установить правило (критерий), которое позволяло бы судить, является ли расхождение между эмпирическим и теоретическим распределениями случайным или значимым. Если расхождение окажется случайным, то считают, что данные наблюдений (выборки) согласуются с выдвинутой гипотезой о законе распределения генеральной совокупности и, следовательно, гипотезу принимают; если же расхождение окажется значимым, то данные наблюдений не согласуются с гипотезой, и ее отвергают.

Критерием согласия называют критерий, который позволяет установить, является ли расхождение эмпирического и теоретического распределений случайным или значимым, т. е. согласуются ли данные наблюдений с выдвинутой статистической гипотезой или не согласуются.

Имеется несколько критериев согласия: критерий хи-квадрат (Пирсона), критерий Колмогорова, критерий Романовского и др. Ограничимся описанием того, как критерий применяется к проверке гипотезы о нормальном распределении генеральной совокупности (критерий применяется аналогично и для других распределений).

Допустим, что в результате наблюдений получена выборка:

Для определенности примем уровень значимости 0,01. Если вероятность, найденная по таблицам, окажется меньше 0,01, то это означает, что в результате влияния случайных причин наступило событие, которое практически невозможно. Таким образом, тот факт, что приняло значение нельзя объяснить случайными причинами; его можно объяснить тем, что генеральная совокупность не распределена нормально и, значит, выдвинутая гипотеза о нормальном распределении генеральной совокупности должна быть отвергнута. Если вероятность, найденная по таблицам, превышает 0,01, то гипотеза о нормальном распределении генеральной совокупности согласуется с данными наблюдений и поэтому может быть принята. Полученные выводы распространяются и на другие уровни значимости.

На практике надо, чтобы объем выборки был достаточно большим и чтобы каждая группа содержала не менее 5-8 значений признака.

Для проверки гипотезы о нормальном распределении генеральной совокупности нужно:

1) вычислить теоретические частоты по формуле (11.3);

4) выбрать уровень значимости;

5) найти по таблице прил. 6 по найденным и вероятность причем если эта вероятность меньше принятого уровня значимости, то гипотезу о нормальном распределении генеральной совокупности отвергают; если вероятность больше уровня значимости, то гипотезу принимают.

Пример 5. Проверить, согласуются ли данные выборки со статистической гипотезой о нормальном распределении генеральной совокупности, из которой извлечена эта выборка:

Следовательно, данные наблюдения согласуются с гипотезой о нормальном распределении генеральной совокупности.

Источник

Теоретические и эмпирические частоты. Критерии согласия

Эмпирические частоты получают в результате опыта (наблюдения). Теоретические частоты рассчитывают по формулам.

Для нормального закона распределения их можно найти следующим образом:

, (_*)

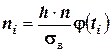
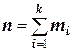
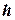
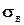
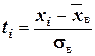
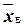
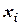
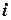
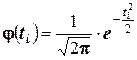
где – сумма эмпирических (наблюдаемых) частот; – разность между двумя соседними вариантами (то есть длина частичного интервала); – выборочное среднее квадратическое отклонение; ; – выборочная средняя арифметическая; – середина -го частичного интервала; значения функции находят по таблице (см. приложения).

Обычно эмпирические и теоретические частоты различаются. Возможно, что расхождение случайно и связано с ограниченным количеством наблюдений; возможно, что расхождение неслучайно и объясняется тем, что для вычисления теоретических частот выдвинута статистическая гипотеза о том, что генеральная совокупность распределена нормально, а в действительности это е так. Распределение генеральной совокупности, которое она имеет в силу выдвинутой гипотезы, называют теоретическим.

Возникает необходимость установить правило (критерий), которое позволяло бы судить, является ли расхождение между эмпирическим и теоретическим распределениями случайным или значимым. Если расхождение окажется случайным, то считают, что данные наблюдений (выборки) согласуются с выдвинутой гипотезой о законе распределения генеральной совокупности и, следовательно, гипотезу принимают. Если же расхождение окажется значимым, то данные наблюдений не согласуются с выдвинутой гипотезой, и её отвергают.

Критерием согласия называют критерий, который позволяет установить, является ли расхождение эмпирического и теоретического распределений случайным или значимым, то есть согласуются ли данные наблюдений с выдвинутой статистической гипотезой или не согласуются.

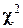
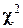
Имеются несколько критериев согласия: критерий (Пирсона), критерий Колмогорова, критерий Романовского и др. Ограничимся описанием того, как критерий применяется к проверке гипотезы о нормальном распределении генеральной совокупности (предлагаем студентам написать рефераты по различным критериям согласия и их применению).

Допустим, что в результате 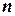наблюдений получена выборка:

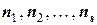
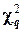
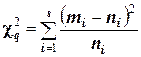
Выдвинем статистическую гипотезу: генеральная совокупность, из которой извлечена данная выборка, имеет нормальное распределение. Требуется установить, согласуется ли эмпирическое распределение с этой гипотезой. Предположим, что по формуле (_*) вычислены теоретические частоты . Обозначим среднее арифметическое квадратов разностей между эмпирическими и теоретическим частотами, взвешенное по обратным величинам теоретических частот:

.

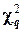
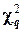
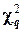
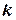
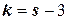
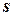
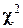
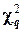
Чем больше согласуются эмпирическое и теоретическое распределения, тем меньше различаются эмпирические и теоретические частоты и тем меньше значение . Отсюда следует, что характеризует близость эмпирического и теоретического распределений. В разных опытах принимает различные, заранее неизвестные значения, то есть является случайной величиной. Плотность вероятности этого распределения (для выборки достаточно большого объёма) не зависит от проверяемого закона распределения, а зависит от параметра , называемого числом степеней свободы. Так при проверке гипотезы о нормальном распределении генеральной совокупности , где – число групп, на которые разбиты данные наблюдений. Существуют таблицы (см. приложения), в которых указана вероятность того, что в результате влияния случайных факторов величина примет значение не меньше вычисленного по данным выборки .

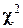
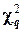
Для определённости примем уровень значимости 0,01. Если вероятность, найденная по таблицам, окажется меньше 0,01, то это означает, что в результате влияния случайных причин наступило событие, которое практически невозможно. Таким образом, тот факт, что приняло значение , нельзя объяснить случайными причинами; его можно объяснить тем, что генеральная совокупность не распределена нормально и, значит, выдвинутая гипотеза о нормальном распределении генеральной совокупности должна быть отвергнута. Если вероятность, найденная по таблицам, превышает 0,01, то гипотеза о нормальном распределении генеральной совокупности согласуется с данными наблюдений и поэтому может быть принята. Полученные выводы распространяются и на другие уровни значимости.

На практике надо, чтобы объём выборки был достаточно большим (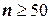) и чтобы каждая группа содержала 5 – 8 значений признака.

Для проверки гипотезы о нормальном распределении генеральной совокупности нужно:

1) вычислить теоретические частоты по формуле (_*);

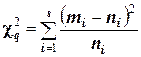
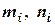
2) вычислить , где – соответственно частоты эмпирические и теоретические;

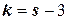
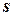
3) вычислить число степеней свободы , где – число групп, на которые разбита выборка;

4) выбрать уровень значимости;

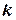
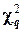
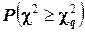
5) найти по таблице (см. приложения) по найденным и вероятность , причём, если эта вероятность меньше принятого уровня значимости, то гипотезу о нормальном распределении генеральной совокупности отвергают; если же вероятность больше уровня значимости, то гипотезу принимают.

ПРИМЕР 5. Проверить, согласуются ли данные выборки со статистической гипотезой о нормальном распределении генеральной совокупности, из которой извлечена выборка:

варианта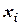

частота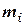

Решение. Вычислим выборочное среднее и выборочную дисперсию:

; .

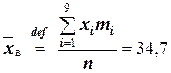
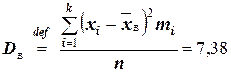
Далее, вычислим теоретические частоты по формуле (_*):

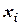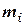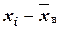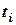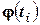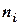– 19,7	– 2,67	0,0113
– 14,7	– 1,99	0,0551
– 9,7	– 1,31	0,1691
– 4,7	– 0,63	0,3271
0,3	0,05	0,3984
5,3	0,73	0,3056
10,3	1,41	0,1476
15,3	2,09	0,0449
20,3	2,77	0,0086

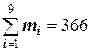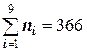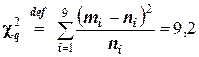
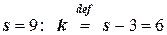
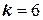
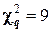
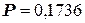
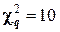
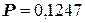
Найдём . Вычислим число степеней свободы, учитывая, что число групп выборки . Уровень значимости примем равным 0,01. По таблице (см. приложения) при и находим вероятность ; при вероятность . Используя линейную интерполяцию, получаем приближённое значение искомой вероятности 0,16 > 0,01.

Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.

[2] Хотим заметить, что далеко не всегда властелины были глупыми людьми, не знающими математики. Так, например, Наполеон был немного математиком, интересовался, в частности, геометрией. Он вёл дискуссии с Лагранжем и Лапласом, когда ещё не был правителем Франции. Как-то в одной из таких дискуссий Лаплас резко оборвал Бонапарта: «Менее всего мы хотим от Вас, генерал, урока геометрии». В дальнейшем Лаплас стал его главным военным инженером.

[3] При доказательстве можно воспользоваться приближенной формулой Стирлинга.

[4] Напомню, что счётным является множество, элементы которого можно пронумеровать числами натурального ряда.

[6] Воспользоваться вторым свойством для функции

[7] Происхождение термина «математическое ожидание» связано с начальным периодом возникновения теории вероятностей (XVI-XVII вв.), когда область её применения ограничивалась азартными играми. Игрока интересовало среднее значение ожидаемого выигрыша или, иными словами, математическое ожидание выигрыша.

[8] Закон распределения.

[9] Нормальное распределение было найдено впервые Муавром в 1733 г. в связи с исследованием предела биномиального распределения. Открытие прошло незамеченным; только в 1809 г. Гауссом и в 1812 г. Лапласом оно было снова открыто в связи с теорией ошибок наблюдений.

Существует известное замечание Липмана, гласящее, «каждый уверен в справедливости закона ошибок: экспериментаторы – потому, что они думают, что это математическая теорема, математики – потому, что они думают, что это экспериментальный факт».

Отметим, что обе стороны совершенно правы, если только это их убеждение не слишком безусловно: при математическом доказательстве (см.центральную предельную теорему) утверждается, что при некоторых ограничениях вправе ожидать нормальное распределение, а статистический опыт показывает, что в действительности распределения являются часто приближённо нормальными. Поэтому, нормальному распределению уделяется большое внимание.

[10] В этом состоит сущность так называемого правила трёх сигм: если случайная величина распределена нормально, то абсолютная величина её отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

На практике правило трёх сигм применяется так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведённом правиле, выполняется, то имеются все основания предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.

[11] Применяется в теории надёжности для описания времени безотказной работы невосстанавливаемых изделий.

[14] Однако ошибочно думать, что увеличивая число измерений можно достичь сколь угодно большой точности. Дело в том, что сам прибор даёт показания лишь с точностью ; поэтому каждый из результатов измерений, а следовательно и их среднее арифметическое, будут получены лишь с точностью, не превышающей точности прибора.

[15] Доказательство впервые было опубликовано в 1713 году.

[16] Доказательство, предложенное Я. Бернулли, было сложным; более простое доказательство было дано П. Чебышевым в 1846 году.

[17] Известно, что произведение двух сомножителей, сумма которых есть величина постоянная, имеет наибольшее значение при равенстве сомножителей.

[18] Одномерную случайную величину иногда называют скалярной случайной величиной.

[19] Интегральная функция распределения.

[20] Дифференциальная функция распределения.

[21] Предполагается, что интегральная функция распределения вероятностей имеет непрерывную смешанную частную производную второго порядка.

[22] Мы записали условные законы распределения случайной величины при условии, что другая случайная величина приняла определённое значение.

[23] Предлагаем все дальнейшие вычисления сделать самостоятельно.

[24] Полученный ряд называется ранжированным.

[25] Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике – соответствие между наблюдаемыми вариантами и их частотами, или относительными частотами.

[26] строится аналогично полигону в прямоугольной системе координат.

[27] или простое среднее отклонение.

[28] Данное распределение называют выборочным.

[29] Полученные выводы применимы и для бесповторной выборки, если её объём значительно меньше объёма генеральной совокупности. Это положение часто используется на практике.

[31] Обычно при выполнении пп. 4 – 7 используют статистику с нормальным распределением, статистику Стьюдента, Фишера.

[32] То есть – с математическим ожиданием.

[33] Критерий применяется аналогично и для других распределений

Источник