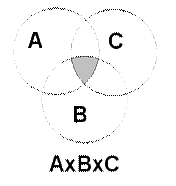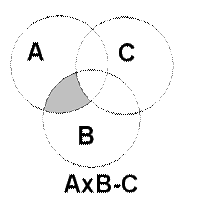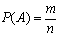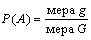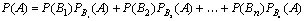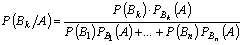Что такое случайное событие в информатике
Случайные события и их вероятности



1. Случайные события
Теория вероятностей— это раздел математики изучающий закономерности массовых случайных событий.
Случайным называется событие, наступление которого нельзя гарантировать. Случайность того или иного события определяется множеством причин, которые существуют объективно, но учесть их все, а также степень их влияния на изучаемое событие, невозможно. К таким случайным событиям относятся: выпадание того или иного числа при бросании игральной кости, выигрыш в лотереи, количество больных, записавшихся на прием к врачу и т.п.
И хотя в каждом конкретном случае трудно предсказать исход испытания, при достаточно большом числе наблюдений можно установить наличие некоторой закономерности. Подбрасывая монету, можно заметить, что число выпадания орла и решки примерно одинаково, а при бросании игральной кости различные грани также появляются, примерно одинаково. Это говорит о том, что случайным явлениям присущи свои закономерности, но они проявляются лишь при большом количестве испытаний. Правильность этого подтверждает закон больших чисел, который лежит в основе теории вероятностей.
Рассмотрим основные термины и понятия теории вероятностей.
Испытанием называется совокупность условий, при которых может произойти данное случайное событие.
События бывают достоверные, невозможные и случайные.
Достоверное событие — это событие, которое в результате испытания непременно должно произойти.
Например,если на игральной кости на всех шести гранях. нанести цифру 1, тогда выпадение цифры 1, при бросании кости, есть событие достоверное.
Например,в ранее рассмотренном примере — это выпадение любой цифры, кроме 1.
Случайное событие — это событие, которое при испытаниях может произойти или не произойти. Те или иные события реализуются с различной возможностью.
События называются несовместными, если в результате данного испытания появление одного из них исключает появление другого.
Например,при бросании монеты выпадение одновременно орла и решки есть события несовместные.
События называются совместными, если в результате данного испытания появление одного из них не исключает появление другого.
Например,при игре в карты появление валета и масти пик — события совместные.
События называются равновозможными, если нет оснований считать, что одно из них происходит чаше, чем другое!
Например,выпадение любой грани игрального кубика есть равновозможные события.
События образуют полную группу событий, если в результате испытания обязательно произойдет хотя бы одно из них и любые два из них несовместны.
Например,при 10 выстрелах в мишень возможно от 0 до 10 попаданий. При бросании игрального кубика может выпасть цифра от 1 до 6. Эти события образуют полную группу.
События, входящие в полную группу попарно несовместных и равновозможных событий, называются исходами, или элементарными событиями. Согласно определению достоверного события, можно считать, что событие, состоящее в появлении одного, неважно какого, из событий полной группы, есть событие достоверное.
Например,при бросании одного игрального кубика выпадает число меньше семи. Это пример достоверного события.
Частным случаем событий, образующих полную группу, являются противоположные события.
Два несовместных события А и 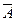
Например,если стипендия начисляется только при получении на экзамене хороших и отличных оценок, то события «стипендия» и «неудовлетворительная или удовлетворительная оценка» — противоположные.
Событие А называется благоприятствующим событию В, если появление события А влечет за собой появление события В.
Например,при бросании игрального кубика появлению нечетного числа благоприятствуют события, связанные с выпадением чисел 1,3 и 5.
2. Операции над событиями
Операции над событиями аналогичны операциям над множествами.
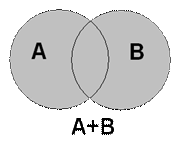
Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из них в результате испытания.
Сумма событий может быть обозначена знаками «+», «È», «или».
На рисунке 1 представлена геометрическая интерпретация с помощью диаграмм Эйлера-Венна. Сумме событий А + В будет соответствовать вся заштрихованная область.

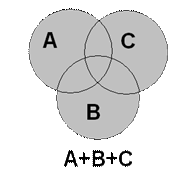
Область пересечения событий А и В соответствует совместным событиям, которые могут произойти одновременно. Аналогично для событий А, В и С имеются совместные события А и В; А и С; В и С; А и В и С, которые могут про изойти одновременно.
Например,в урне находятся белые, красные и синие шары. Возможны следующие события: А — вынут белый шар; В — вынут красный шар; С — вынут синий шар. Событие В + С означает, что произошло событие — вынут цветной шар или вынут не белый шар.
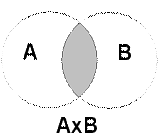
Произведением нескольких событий называется событие которое состоит в совместном наступлении всех этих событий в результате испытания.
Произведение событий может быть обозначено знаками «х», «∩», «и».
Геометрическая интерпретация произведения событий представлена на рис. 2.
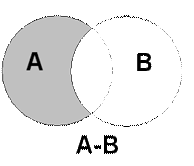
Разностью двух событий А-В называется событие, состоящее из исходов, входящих в А, но не входящих в В.
На рис. 3 представлена иллюстрация разности событий с помощью диаграмм Эйлера-Венна.
Разностью двух событий А-В является заштрихованная область А без той части, которая входит в событие В. Разность между произведением событий А и В и событием С будет совместная площадь события А и события В без совместной с нею площадью события С.
3. Определение вероятности события
Классическое определение вероятности заключается в следующем. Если известны все возможные исходы испытания и нет оснований считать, что одно случайное событие появлялось бы чаще других, т.е. события равновозможны и несовместны, то имеется возможность аналитического определения вероятности события.
Вероятностью Р(А)события Аназывается отношение числа благоприятствующих исходов т к общему числу равновозможных несовместных исходов п:
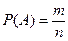
Свойства вероятности:
1. Вероятность случайного события А находится между 0 и 1.
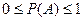
2. Вероятность достоверного события равна 1.
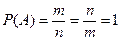
3. Вероятность невозможного события равна 0.
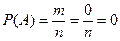
Интегрированный урок (статистика + информатика) в 7-м классе по теме «Случайные события. Вероятность и частота»
Учащиеся 7 класса участвуют в проектно-исследовательской работе лаборатории «Пифагор». Учителем Мирсалимовой Еленой Николаевной, которая ведет у учащихся и математику и информатику, организована серия интегрированных исследовательских уроков. На 1 уроке учащиеся познакомились с темами: «Случайные события», «Игральные кости», провели 100 опытов по бросанию игральной кости, предварительно выдвинув рабочую гипотезу о шансах выпадения 6-ки, и в программе Excel MS каждый на своём компьютере организовал таблицу результатов своих опытов.
Тип урока: изучение нового материала.
Цель урока: подготовить учащихся к решению практических задач в условиях информационного общества, научить учащихся пользоваться компьютерной технологией по обработке и анализу информации, уметь пользоваться схемой проектно- исследовательской деятельности.
Задачи урока:
Учебная группа: учащиеся 7 класса (полкласса), информатика изучается 3-й год, статистика 1-й год.
Оснащение урока (ТСО): урок проходит в компьютерном классе (12 ПК), интерактивная доска Inter Write, мультимедийный проектор, локальная сеть, презентация учителя к уроку, Excel- ие файлы с таблицами и графиками к уроку.
Содержание этапов урока:
1. Организационный этап. Приветствие. Учитель представляется как научный руководитель проектно-исследовательской лаборатории «Пифагор».
2. Постановка проблемы. Сегодня у нас 2-е заседание лаборатории «Пифагор», которая изучает в настоящее время «случайные события». Учитель уточняет, что дети знают о случайных событиях. Форма организации учебной деятельности: учитель показывает презентацию и задает вопросы – класс монологически высказывается.
Про одни события мы твердо знаем, что они произойдут, что лето кончится и наступит осень, в наступлении других событий мы не так уверены.
Слайд 2. (Приложение 1) Какие события мы называем случайными?
Слайд 3. (Приложение 1) Является ли случайным событием «Меня завтра спросят на уроке»?
Слайд 4. (Приложение 1) Является ли случайным событие «Летом у меня будут каникулы»?
Слайд 5. (Приложение 1) Является ли случайным событие «Мне сегодня встретится черная кошка»?
Слайд 6. (Приложение 1) Вообразите, что вы отправились на рыбную ловлю. Какие случайные события могут произойти при этом?
Слайд 7. Приведите примеры случайных событий из вашей школьной жизни.
3. Подготовка к восприятию нового материала. Совершенно верно. Про случайные события мы не можем сказать заранее, произойдет оно или нет. Но мы можем говорить о шансах наступления этого события.
Слайд 8-9-10 (фото). (Приложение 1)
На прошлом заседании лаборатории «Пифагор» мы проводили случайный эксперимент или опыт, точнее 100 опытов бросания игральной кости. Мы хотели узнать шансы выпадения 6-ки.
Слайд 11 (схема исследовательской работы). (Приложение 1)
Перед проведением опытов мы выдвинули рабочую гипотезу и записали её в тетрадь.
Это был мозговой штурм. Причитайте рабочую гипотезу из своей тетради. А что получилось из опыта? (каждый ученик читает из своей тетради)
Учитель показывает на интерактивной доске все действия.
Посмотрим и проанализируем результаты своей работы. Озвучим, какие шансы выпадения 6-ки получили.
5. Изучение нового материала (статистика) продолжается за партой. «Частота и вероятность случайного события»
Слайд 12. (Приложение 1)
В теории вероятностей шансы того, что случайное событие произойдёт, выражают числом. Это число называют вероятностью случайного события. Если событие никогда не наступает (его шансы равны 0), то вероятность этого события полагают равной 0. Такое событие называют невозможным. Если же событие наступает всегда, его вероятность полагают равной 1. Такое событие называют достоверным. Вероятность остальных событий – это числа между 0 и 1. Т.о., вероятность случайного события – это числовая мера правдоподобия.
Слайд 13. (Приложение 1)
Для кубика почти очевидно, что все исходы имеют одну и ту же вероятность 1/6. На чём основана такая убеждённость? Прежде всего, из-за симметрии кубика. Каждая из 6- ти граней ничем не лучше (и не хуже) любой из 5 оставшихся. Это даёт нам все основания утверждать, что 6 исходов этого опыта имеют одинаковую вероятность, или, как говорят, равновозможны. Иногда вероятность события можно рассчитать математически, а иногда приходится приближённо узнавать их из эксперимента. Мы сейчас с вами это и проделаем. Всякое случайное событие связано с определёнными условиями. Вне этих условий это событие вообще невозможно. О вероятности выпадения 6-ки в наших опытах можно говорить, только если эту кость бросают. Создав такие условия, мы тем самым произвели некоторый случайный эксперимент, или опыт. Повторяя этот опыт много раз, мы увидим, сколько раз интересующее нас событие происходит, а сколько раз не происходит. (Сегодня каждый из вас зачитывал свои результаты случайных опытов).
Слайд 14. (Приложение 1)
Пусть, например, мы провели опыт 100 раз и некоторое событие С произошло в этих опытах 18 раз. Отношение числа тех опытов, в которых событие С произошло, к общему числу проведённых опытов равно в данном случае
Ребята, через нашу локальную сеть я собрала в одну таблицу результаты ваших 100 опытов, получила 1000 опытов бросания игральной кости. Эта таблица перед вами. Подсчитана частота в 10 различных сериях по 100- кратному бросанию кубика. Из этих результатов видно, что частота может значительно колебаться от серии к серии (в нашем примере от 0,14 до 0,167). Но, с другой стороны, совершенно очевидно, что эти колебания происходят около некоторого числа, для вас вряд ли будет неожиданностью, если я объявлю это число 0,166.
(Приложение 2) Перед вами динамика изменения частоты выпадения 6-ки в длинной серии из 1000 опытов по подбрасыванию игральной кости (я использую общие результаты исследования). Частота выпадения 6-ки пересчитывалась после каждых 100 опытов о наносилась на график, который так же как мы сегодня на уроке научились, строился в Excel.
По графику видно, что с ростом числа опытов частота начинает постепенно стабилизироваться. Правда, назвать точно это число невозможно. Тем не менее, видно, что оно лежит где-то в районе 0,165- 0,167. Для более точной оценки следует, как вы думаете, что сделать? Верно, увеличить количество опытов.
Итог урока. Итак, сегодня наша лаборатория «Пифагор» не заканчивает свою работу. На следующем заседании мы будем готовиться к конференции, создавать презентацию в Power Point, включая в неё результаты опытов, анализ исследований, диаграммы, графики, фото с урока. Спасибо всем исследователям!
Случайное событие
Случа́йное собы́тие — подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности.
Случайное событие, которое никогда не реализуется в результате случайного эксперимента, называется невозможным и обозначается символом 

Содержание
Определение
Математически случайное событие — подмножество пространства элементарных исходов случайного эксперимента; элемент алгебры или сигма-алгебры событий 



Пример
Случайный эксперимент состоит в бросании игральной кости: пример случайного события — выпавшее число чётно; события «Выпала единица», «Выпала двойка» и т. д. — элементарные исходы эксперимента; совокупность всех событий «Выпала 1»..«Выпала 6» — полная группа событий.
См. также
Ссылки
Полезное
Смотреть что такое «Случайное событие» в других словарях:
случайное событие — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] случайное событие Событие, которое при осуществлении некоторых условий может произойти либо не произойти, и для которого имеется определенная… … Справочник технического переводчика
Случайное событие — [random event, chance event] — событие, которое при осуществлении некоторых условий может произойти либо не произойти, и для которого имеется определенная вероятность его наступления. То же (в разных источниках) исход, случай, результат… … Экономико-математический словарь
СЛУЧАЙНОЕ СОБЫТИЕ — (в теории вероятностей) событие, которое может при осуществлении данных условий (т. е. при данном испытании) как произойти, так и не произойти и для которого имеется определенная вероятность его наступления. Наличие у случайного события… … Большой Энциклопедический словарь
случайное событие — (в теории вероятностей), событие, которое может при осуществлении данных условий (то есть при данном испытании) как произойти, так и не произойти и для которого имеется определенная вероятность его наступления. Наличие у случайного события… … Энциклопедический словарь
случайное событие — atsitiktinis įvykis statusas T sritis fizika atitikmenys: angl. accidental event; chance event; random event vok. zufälliges Ereignis, n rus. случайное событие, n pranc. événement aléatoire, m … Fizikos terminų žodynas
Случайное событие — в теории вероятностей, событие, которое может при данных условиях как произойти так и не произойти и для которого имеется определённая Вероятность р (0 ≤ p ≤ 1) его наступления при данных условиях. Наличие у С. с. А определённой… … Большая советская энциклопедия
СЛУЧАЙНОЕ СОБЫТИЕ — любая комбинация исходов нек рого опыта, имеющая определенную вероятность наступления. Пример 1. При бросании двух игральных костей каждый из 36 исходов опыта может быть представлен нарой (i, j), где i число очков на верхней грани цервой кости, а … Математическая энциклопедия
СЛУЧАЙНОЕ СОБЫТИЕ — (в теории вероятностей), событие, к рое может при осуществлении данных условий (т. е. при данном испытании) как произойти, так и не произойти и для к рого имеется определ. вероятность его наступления. Наличие у С. с. определ. вероятности р… … Естествознание. Энциклопедический словарь
Случайное событие — (в теории вероятностей) событие, которое может, с определенной долей вероятности, в условиях испытания как произойти, так и не произойти; отдельный исход (результат) испытания. См. Случайная величина. Случайный процесс … Начала современного естествознания
событие — Факт, состоящий в том, что нечто произошло или в проблемной области, или в среде, или в информационной системе. [ГОСТ 34.320 96] событие 1. См. Случайное событие. 2. В сетевом планировании и управлении — промежуточный или окончательный… … Справочник технического переводчика
Тема 8. СОБЫТИЕ И ВЕРОЯТНОСТЬ
8.1. Понятие о случайном событии
Наблюдение явления, опыт, эксперимент, которые можно провести многократно, в теории вероятностей принято называть испытанием. Примеры: сдача экзамена, наблюдение за дорожно-транспортными происшествиями, выстрел из винтовки, бросание игрального кубика, педагогический эксперимент.
Результат, исход испытания называется событием. Примеры: успешная сдача экзамена, дорожно-транспортные происшествия со смертельным исходом, попадание в цель, появление того или иного числа очков на брошенной игральной кости, получение результата при проведении педагогического эксперимента.
Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании. Примеры: совместные события: идет дождь и идет снег, человек ест и человек читает, число целое и четное; несовместные события: день и ночь, человек читает и человек спит, число иррациональное и четное.
Два события называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит. Примеры: если сейчас день, то сейчас не ночь; если человек спит, то в данный момент он не читает; если число иррациональное, то оно не является четным.
Событие называется достоверным, если в данном испытании оно является единственно возможным его исходом. Событие называется невозможным, если в данном испытании оно заведомо не может произойти. Примеры: если в урне все шары белые, то достать белый шар является достоверным событием, а достать черный шар является невозможным событием; если человек прыгнул в воду, то выйти мокрым является достоверным событием, а выйти сухим является невозможным событием.
Событие называется случайным, если его наступление или ненаступление в некотором испытании (эксперименте) зависит от ряда случайных факторов. Примеры: успешная сдача экзамена; выигрыш в лотерее; рождения мальчика или девочки; всхожесть семян; попадание в цель и т. д.
8.2. Определение вероятности 
События, образующие полную группу попарно несовместных и равновозможных событий, будем называть элементарными событиями.
Классическое определение вероятности
Вероятностью P(A) события A называется отношение числа элементарных событий m, благоприятствующих событию A, к числу всех элементарных событий n:
Вероятность достоверного события равна 1.
Вероятность невозможного события равна 0.
Вероятность случайного события больше 0 и меньше 1.
Статистическое определение вероятности
Классическое определение вероятности не является пригодным для изучения произвольных случайных событий. Например, оно неприемлемо, если результаты испытания не равновозможны. В таких случаях используется статистическое определение вероятности. Пусть проводится n опытов, событие A наступило m раз, тогда
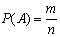
Геометрическое определение вероятности
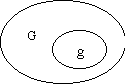
Если в результате проведения испытаний наблюдается произвольный исход из некоторого бесконечного множества, то можно сказать, что пространство элементарных исходов может быть некоторой областью G, а под событием А можно понимать исходы, входящие в область g. Пусть на область G наугад брошена «точка»; приняв равновозможность вариантов, естественно считать, что вероятность попадания в область g можно найти по формуле, называемой геометрической вероятностью:
Области могут быть различной размерности (одно-, двух- или трехмерного измерения) и, в зависимости от выбора размерности меры, могут принимать значения либо длины, либо площади, либо объема. Для конкретного испытания размерность мер g и G должна быть одна.
8.3. Свойства вероятности 
Теорема. Вероятность суммы двух несовместных событий A и B равна сумме вероятностей этих событий: P (A + B) = P(A) + P(B).
Следствие. Сумма вероятностей противоположных событий А и равна единице:
Вероятность суммы полной группы событий равна 1.
Произведением событий А и В называется событие С = АВ, состоящее в том, что в результате испытания произошло и событие А и событие В.
Два события A и B называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события A и B называются зависимыми.
Чаще всего зависимые испытания происходят тогда, когда тянут из одной колоды, не возвращая карты в колоду, вытаскивают из одной урны и т. д.
Теорема. Вероятность произведения двух независимых событий A и B равна произведению их вероятностей:
Теорема. Вероятность произведения двух зависимых событий A и B равна произведению вероятности одного из них на условную вероятность другого, найденного в предположении, что первое событие уже наступило:
Теорема. Вероятность суммы двух совместных событий A и B равна сумме вероятностей этих событий минус вероятность их произведения
Теорема (формула полной вероятности). Вероятность события A, которое может наступить лишь при условии появления одного из n попарно несовместных событий B1, B2,…, Bn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A:
Вопросы 
1. Может ли событие быть одновременно и невозможным и достоверным?
2. Входит ли в понятие суммы событий (А + В) событие, состоящее в одновременном наступлении события А и события В?
3. Приведите пример полной группы событий для выбранного Вами испытания.
4. Исходя из формулы определения вероятности, объясните, почему значение вероятности находится в пределах от 0 до 1.
5. Часто ли случается, что наступление какого-либо события зависит от ряда причин? Приведите пример.
6. С помощью какой формулы можно выяснить наиболее вероятную причину уже наступившего события?