Что такое случайные числа
Случайные числа (random numbers)
Психологи часто пользуются С. ч. для решения разных задач. Напр., можно сформировать случайную выборку, нумеруя потенциальных испытуемых в совокупности, а затем отбирая на основе таблицы С. ч. реальных испытуемых для включения в ее состав. Такой случайный процесс гарантировал бы получение случайной (непредвзятой) выборки — необходимого, по существу, условия всех видов статистического анализа.
С. ч. тж могут использоваться для распределения испытуемых по группам (соответственно условиям) в эксперименте, для выбора уровней предъявления независимой переменной или для эмпирического построения выборочных распределений статистик путем случайного извлечения выборок из совокупности с известным распределением.
См. также Вероятность, Статистика в психологии
Смотреть что такое «Случайные числа (random numbers)» в других словарях:
СЛУЧАЙНЫЕ ЧИСЛА — (random numbers) см. Выборочная совокупность и выборка … Большой толковый социологический словарь
Псевдослучайные числа — Генератор псевдослучайных чисел (ГПСЧ, англ. Pseudorandom number generator, PRNG) алгоритм, генерирующий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).… … Википедия
Генератор псевдослучайных чисел — (ГПСЧ, англ. Pseudorandom number generator, PRNG) алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному). Современная информатика… … Википедия
Датчик случайных чисел — Генератор псевдослучайных чисел (ГПСЧ, англ. Pseudorandom number generator, PRNG) алгоритм, генерирующий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).… … Википедия
Криптостойкий генератор псевдослучайных чисел — Генератор псевдослучайных чисел (ГПСЧ, англ. Pseudorandom number generator, PRNG) алгоритм, генерирующий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).… … Википедия
Псевдослучайное число — Генератор псевдослучайных чисел (ГПСЧ, англ. Pseudorandom number generator, PRNG) алгоритм, генерирующий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).… … Википедия
Криптографически стойкий генератор псевдослучайных чисел — (англ. Cryptographically secure pseudorandom number generator, CSPRNG) это генератор псевдослучайных чисел с определенными свойствами, позволяющими использовать его в криптографии. Многие прикладные задачи криптографии требуют случайных… … Википедия
Задача о разорении игрока — Задача о разорении игрока задача из области теории вероятностей. Подробно рассматривалась российским математиком А. Н. Ширяевым в монографии «Вероятность»[1] … Википедия
Краткая история случайных чисел
«Когда я задался целью получить действительно случайное число, то не нашел для этого ничего лучшего, чем обычная игральная кость» — писал в 1890 году Фрэнсис Гальтон в журнале Nature. «После того, как кости встряхивают и бросают в корзинку, они ударяются друг о друга и о стенки корзинки столь непредсказуемым образом, что даже после легкого броска становится совершенно невозможным предопределить его результат».

(Игральные кости времён Римской Империи)
Как мы можем сгенерировать равномерную последовательность случайных чисел? Случайность, столь прекрасная в своём многообразии, часто встречается в живой природе, но её не всегда легко было извлечь искусственным путём. Самые древние из игральных костей были найдены на Среднем Востоке, и они датируются примерно 24 столетием до нашей эры. Другим примером может быть Китай, где ещё в 11 столетии до нашей эры применялось разбивание ударом черепашьего панциря, с дальнейшей интерпретацией размера полученных случайных частей. Столетиями позже люди разрубали несколько раз стебли растений и сравнивали размеры полученных частей.
Но к середине 40-ых годов ХХ столетия человечеству понадобилось значительно больше случайных чисел, чем можно было получить от бросков костей или разрезания стеблей. Американский аналитический центр RAND создал машину, которая была способна генерировать случайные числа с помощью использования случайного генератора импульсов (что-то вроде электронной рулетки). Они запустили её и через какое-то время получили достаточное количество случайных чисел, которые опубликовали в виде книги «Один миллион случайных чисел и сто тысяч нормальных отклонений».

Другая похожая машина, ERNIE, построенная в знаменитом сегодня Блетчли-парке в 40-ых годах ХХ века, использовалась для генерации случайных чисел в британской лотерее Premium Bond. Для того, чтобы развеять страхи по поводу случайности и честности результатов, была даже снята документальная лента «The Importance of Being E.R.N.I.E.». Сегодня её можно посмотреть на Youtube:
В 1951 году случайность наконец была формализована и воплощена в реальном компьютере Ferranti Mark 1, который поставлялся со встроенным генератором случайных данных на основе дробовых шумов и инструкцией, позволяющей получить 20 случайных бит. Этот функционал был разработан Аланом Тьюрингом. Его коллега Кристофер Стрэчи применил его для создания «генератора любовных писем». Вот пример текста, который был сгенерирован данной программой:
Но генератор случайных чисел Тьюринга не делал программистов тех лет счастливыми, поскольку привносил в и так новые и нестабильные компьютерные системы фактор ещё большей нестабильности. Желая добиться стабильной работы некоторой программы — без отладчиков и со случайными данными — никогда нельзя было достичь повторяемости результатов. Тогда возникла следующая мысль: «А что, если генератор случайных чисел может быть представлен в виде некоторой детерминированной функции?» Тогда получилось бы, что, с одной стороны, генерируемые числа имели бы признаки случайных, но с другой стороны, при одинаковой инициализации генератора данные последовательности были бы каждый раз одни и те же. Так появились генераторы псевдослучайных чисел (ГПСЧ).
Джон фон Нейман разработал ГПСЧ в 1946 году. Его идеей было начать с некоторого числа, взять его квадрат, отбросить цифры из середины результата, снова взять квадрат и отбросить середину, и т.д. Полученная последовательность, по его мнению, обладала теми же свойствами, что и случайные числа. Теория фон Неймана не выдержала испытания временем, поскольку какое бы начальное число вы не выбрали, сгенерированная таким образом последовательность вырождалась в короткий цикл повторяющихся значений, вроде 8100, 6100, 4100, 8100, 6100, 4100,…
Полностью избежать циклов невозможно, когда мы работаем с детерминированной функцией, чьи последующие значения основаны на предыдущих. Но что, если период цикла будет столь большим, что на практике это уже не будет иметь значения?
Математик Деррик Генри Лемер развил эту идею в 1949 году с изобретением линейного конгруэнтного метода. Вот генератор псевдослучайных чисел, основанный на подходе Лемера и написанный на Javascript:
Вы можете заметить в коде ряд «магических констант». Эти числа (как правило, простые) выбирались таким образом, чтобы максимизировать период цикла до повторения последовательности результатов. Данный генератор использует в качестве начального значения текущее время и имеет период около 2^31. Он стал популярным с выходом JavaScript 1.0, поскольку он тогда ещё не имел встроенной функции Math.random(), а все ведь хотели, чтобы их рекламные баннеры сменялись случайным образом. «Я не использовал бы этот алгоритм для чего-то связанного с безопасностью, но для многих применений его достаточно», — писал автор вышеуказанного кода Paul Houle.
Но Интернет как раз требовал чего-то, связанного с безопасностью. SSL появился в 1995 году и его реализация требовала высококачественного генератора псевдослучайных чисел. Это привело к серии достаточно диких экспериментов в данной области. Если вы посмотрите на патенты, связанные с генерацией случайных чисел, выданные в те времена, то получите ощущение, будто смотрите на осовремененные попытки построения первого самолёта.
Большинство популярных процессоров в 90-ых годах не имели специальной инструкции для генерации случайных чисел, так что выбор хорошего начального значения для генератора псевдослучайных чисел имел очень важное значение. Это вылилось в проблемы с безопасностью, когда Phillip Hallam-Baker обнаружил, что в браузере Netscape (доминирующем в то время) реализация SSL использовала для инициализации ГПСЧ комбинацию текущего времени и ID своего процесса. Он показал, как хакер может легко подобрать это значение и расшифровать SSL-трафик. Угадывание начального значения алгоритма генерации псевдослучайных чисел — до сих пор популярная атака, хотя с годами она стала слегка сложнее. Вот пример удачной атаки, опубликованный на Hacker News в 2009 году.
В 1997 году программисты были ограничены в способах получения по-настоящему случайных чисел, так что команда SGI создала LavaRand, который состоял из вебкамеры, направленной на пару лава-ламп, стоявших рядом на столе. Картинка с этой камеры была отличным источником энтропии — Настоящим Генератором Случайных Чисел, таким же, как у Тьюринга. Но в этот раз получалось генерировать 165 Кб случайных чисел в секунду. Изобретение было тут же запатентовано.
Большинство экспериментов в этой области не выдержали испытания временем, но один ГПСЧ, названный Вихрем Мерсенна и разработанный в 1997 году Макото Мацумото и Такудзи Нисимура, смог удержать пальму первенства. В нём сочетались производительность и качество результатов, что позволило ему быстро распространиться на многие языки и фреймворки. Вихрь Мерсенна является витковым регистром сдвига с обобщённой отдачей и генерирует детерминированную последовательность с огромным периодом цикла. В текущей реализации период равен 2¹⁹⁹³⁷− 1 и именно эта реализация входит сегодня в большинство языков программирования.
В 1999 году Intel добавил аппаратный генератор случайных чисел в чипсет i810. Это было хорошо, поскольку данная реализация давала по-настоящему случайные числа (на основе температурных шумов), но работало не настолько же быстро, как программные ГПСЧ, так что большинство криптоприложений всё ещё используют ГПСЧ, которые теперь, по крайней мере, можно инициализировать начальным значением от аппаратного генератора случайных чисел.
Это приводит нас к понятию криптографически-безопасного генератора псевдослучайных чисел (КБГПСЧ). (Ох уж эти аббревиатуры! Не удивительно, что компьютерные науки кажутся некоторым людям скучными.) КБГПСЧ стали очень популярными в эпоху SSL. Каким требованиям должен удовлетворять КБГПСЧ? Ну вот вам 131-страничный документ с этими требованиями, развлекайтесь. Как вы уже понимаете, требований не мало. Например, тот же Вихрь Мерсенна им не удовлетворяет, поскольку, имея достаточно большую последовательность сгенерированных им чисел, можно угадать следующее число.
В 2012 году INTEL добавил в свои чипы инструкции RDRAND и RDSEED, позволяющие получить настоящие случайные числа на основе тех же колебаний температуры, но теперь уже на скорости до 500 Мб/с, что должно бы сделать применение программных ГПСЧ ненужным. Но в обществе бродят слухи и сомнения в честности этих инструкций. Нет ли в них специально сделанной закладки для NSA? Никто не может сказать этого точно. Вернее, кто-то, наверное, может, но он точно не напишет об этом в Твиттере.

(Случайные данные полученные от аппаратного генератора случайных чисел Redoubler)
В последние годы начали появляться также аппаратные генераторы случайных чисел от сторонних производителей и даже полностью открытые (как в плане софта, так и аппаратной части). Сила этих продуктов именно в открытости: можно изучить их самостоятельно и даже построить дома самому из общедоступных компонентов. Примерами могут быть REDOUBLER и Infinite Noise TRNG.
Сегодня люди всё ещё ведут дискуссии о том, какой именно генератор случайных чисел стоит использовать в той или иной системе, ядре ОС, языке программирования, криптографической библиотеке и т.д. Есть много вариантов алгоритмов, заточенных на скорость, экономию памяти, безопасность. И каждый из них постоянно подвергается атакам хакеров и специалистов по безопасности. Но для ежедневных задач, не связанных с безопасностью, вы вполне можете положиться на данные из /dev/random или функции rand(), доступных на большинстве платформ. Это даст вам достаточно большую и случайную последовательность данных, которая бы сделала в своё время счастливым Алана Тьюринга.
Что такое ГСЧ – как работает генератор случайных чисел
Алгоритм генератора случайных чисел часто используется в видеоиграх, где он устанавливает разные результаты каждый раз, когда его запускают. Возможно, вы заметили, что даже если вы играете на одном уровне в игре, каждый раз, когда вы пытаетесь выполнить миссию, он не будет одинаковым. Различия не будут наблюдаться в локации или требованиях к миссии, но они будут наблюдаться в количестве приближающихся врагов и областях их появления, изменениях климата и различных препятствиях, которые встречаются между ними. Это делает игру более захватывающей и интересной.
В противном случае, после нескольких попыток игра покажется скучной, так как вы сможете предсказать события, которые произойдут дальше. Это может показаться простым, но для компьютера – генерировать случайные числа – это сложная задача, требующая следовать точным инструкциям, закодированным в нём.
Истинный ГСЧ против псевдо ГСЧ
Есть два типа генераторов случайных чисел: истинные и псевдо.
Какие приложения используют ГСЧ
Не во всех играх используется генератор случайных чисел, что делает их менее конкурентоспособными и часто утомительными, однако, новые игры почти всегда идут с генератором случайных чисел. Многие приложения и игры выигрывают от случайности, поскольку они могут приносить интерес и прибыль только в том случае, если они случайны:
Помимо игровых приложений, есть код случайных чисел в JavaScript, используемый разработчиками и кодировщиками во всём мире для включения генератора случайных чисел в их программы. У Google есть свой очень интересный инструмент, который также основан на теории случайных чисел JavaScript и может генерировать случайные числа. Этот инструмент может пригодиться, когда вы играете в игры с друзьями и семьей. Чтобы посмотреть ГСЧ Google, нажмите здесь.
Манипуляции с ГСЧ
Я уже обсуждал различия между истинным ГСЧ и псевдо ГСЧ и тот факт, что в играх используется псевдо ГСЧ, основанный на алгоритме. Некоторые увлеченные геймеры используют утилиты эмуляции для анализа игр и выявления лазеек, которые можно использовать для управления результатами, даже если используется алгоритм генератора случайных чисел.
ГСЧ на основе алгоритма использует начальное число, которое представляет собой комбинацию определенных факторов и генерирует результат в игре. Это применяемые законы математики, и поскольку 1+1 всегда равно 2, аналогично, если известны факторы в игре, которые приносят желаемый результат, то вы всегда можете достичь того же результата.
Например, если игра требует от игрока выбрать определенного персонажа с определенными усилениями, и результатом будет легкая битва с боссом, то этот шаблон будет постоянным, и все, кто выберет одни и те же варианты, будут иметь одинаковые результаты. Но, для обычного игрока это было бы невозможно, и псевдо-ГСЧ всегда казался бы истинным ГСЧ.
Почему геймеры ненавидят ГСЧ
Геймеров можно разделить на соревнующихся игроков, спидраннеров и средних игроков. Любой конкурентоспособный игрок, овладевший техникой игры и движениями, захочет бросить вызов другим игрокам и побеждать на основе навыков и, несомненно, возненавидит игру, если на результат повлияет генератор случайных чисел. Точно так же спидраннер хотел бы завершить игру как можно скорее, но алгоритм генератора случайных чисел включает тормоза, создавая каждый раз неизвестные и неожиданные сценарии в игре.
В идеале геймеры хотели бы уменьшить количество случаев, когда они сталкиваются со средством генерации случайных чисел в игре, чтобы держать весь игровой процесс и результат под своим контролем. Но, это возможно лишь до определенной степени. И когда геймер часами осваивает игрового персонажа и его движения, он больше всего расстраивается, когда случается что-то случайное, и вся стратегия нарушается. Иногда это тоже действует как благословение, но обычно это проклятие.
Кто такой RNGesus?
Обычные игроки, которые играют только для того, чтобы развлечься или скоротать время, не заботятся о результате игры. Но, опытные профессиональные игроки ненавидят проигрывать только потому, что удача была не в их пользу.
Игроки, которые проигрывают, часто винят в своих поражениях злой ГСЧ, который выгоден их противникам. Там где зло, должен быть Бог – RNGesus.
Среди геймеров во всем мире появился новый термин, RNGesus, который больше соответствует игре слов с «Иисусом». Поскольку Иисус Христос считается нашим спасителем в реальном мире, RNGesus – это вообразимая сущность, созданная для спасения игроков от пагубных последствий ГСЧ. Это нигде не доказывается, но началось как миф, а теперь распространилось по игровому сообществу, как лесной пожар.
Окончательный вердикт по ГСЧ – хорошо или плохо?
На этот вопрос сложно ответить, и определенно не может быть одного и того же ответа для всех. В то время как среднестатистические геймеры утверждают, что это хорошо, другим нравится соревновательный дух.
Алгоритм генератора случайных чисел действительно сохраняет непредсказуемость и интересность каждый раз, когда вы играете на одном уровне. Он стал важной частью многих игр, предлагая разнообразие, например, головоломки, карточные игры, ролевые игры и многие другие. Но, для геймеров, которые верят в навыки как в единственный способ пройти игру, ГСЧ подрывает их потенциал, когда вытаскивает что-то случайное из коробки.
Игры предназначены для развлечения и удовольствия. Если у вас хороший ГСЧ, вы сможете получить лучшие варианты, несмотря на низкие шансы. В случае плохого ГСЧ, вы получите худший результат, даже если вы играли в игру именно так, как должно. Правда в том, что это не то, что можно воспринимать так серьёзно, особенно если оно основано на алгоритме генератора случайных чисел.
Как компьютер генерирует случайные числа
Что такое случайность в компьютере? Как происходит генерация случайных чисел? В этой статье мы постарались дать простые ответы на эти вопросы.
В программном обеспечении, да и в технике в целом существует необходимость в воспроизводимой случайности: числа и картинки, которые кажутся случайными, на самом деле сгенерированы определённым алгоритмом. Это называется псевдослучайностью, и мы рассмотрим простые способы создания псевдослучайных чисел. В конце статьи мы сформулируем простую теорему для создания этих, казалось бы, случайных чисел.
Определение того, что именно является случайностью, может быть довольно сложной задачей. Существуют тесты (например, колмогоровская сложность), которые могут дать вам точное значение того, насколько случайна та или иная последовательность. Но мы не будем заморачиваться, а просто попробуем создать последовательность чисел, которые будут казаться несвязанными между собой.
Часто требуется не просто одно число, а несколько случайных чисел, генерируюемых непрерывно. Следовательно, учитывая начальное значение, нам нужно создать другие случайные числа. Это начальное значение называется семенем, и позже мы увидим, как его получить. А пока давайте сконцентрируемся на создании других случайных значений.
Создание случайных чисел из семени
Один из подходов может заключаться в том, чтобы применить какую-то безумную математическую формулу к семени, а затем исказить её настолько, что число на выходе будет казаться непредсказуемым, а после взять его как семя для следующей итерации. Вопрос только в том, как должна выглядеть эта функция искажения.
Давайте поэкспериментируем с этой идеей и посмотрим, куда она нас приведёт.
Функция искажения будет принимать одно значение, а возвращать другое. Назовём её R.
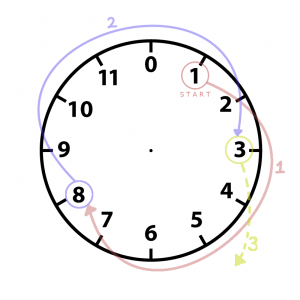
Числовой круг
Посмотрим на циферблат часов: наш ряд начинается с 1 и идёт по кругу до 12. Но поскольку мы работаем с компьютером, пусть вместо 12 будет 0.
Теперь начиная с 1 снова будем прибавлять 7. Прогресс! Мы видим, что после 12 наш ряд начинает повторяться, независимо от того, с какого числа начать.
Здесь мы получаем очень важно свойство: если наш цикл состоит из n элементов, то максимальное число элементов, которые мы можем получить перед тем, как они начнут повторяться это n.
Теперь давайте переделаем функцию R так, чтобы она соответствовала нашей логике. Ограничить длину цикла можно с помощью оператора модуля или оператора остатка от деления.
Если вы попробуете несколько разных значений, то сможете увидеть одно свойство: m и с должны быть взаимно простыми.
До сих пор мы делали «прыжки» за счёт добавления, но что если использовать умножение? Умножим х на константу a.
Свойства, которым должно подчиняться а, чтобы образовался полный цикл, немного более специфичны. Чтобы создать верный цикл:
Эти свойства вместе с правилом, что m и с должны быть взаимно простыми составляют теорему Халла-Добелла. Мы не будем рассматривать её доказательство, но если бы вы взяли кучу разных значений для разных констант, то могли бы прийти к тому же выводу.
Выбор семени
Настало время поговорить о самом интересном: выборе первоначального семени. Мы могли бы сделать его константой. Это может пригодиться в тех случаях, когда вам нужны случайные числа, но при этом нужно, чтобы при каждом запуске программы они были одинаковые. Например, создание одинаковой карты для каждой игры.
Конечный результат
Когда мы применяем функцию к её результату несколько раз, мы получаем рекуррентное соотношение. Давайте запишем нашу формулу с использованием рекурсии:
То, что мы сделали, называется линейным конгруэнтным методом. Он очень часто используется, потому что он прост в реализации и вычисления выполняются быстро.
В разных языках программирования реализация линейного конгруэнтного метода отличается, то есть меняются значения констант. Например, функция случайных чисел в libc (стандартная библиотека С для Linux) использует m = 2 ^ 32, a = 1664525 и c = 1013904223. Такие компиляторы, как gcc, обычно используют эти значения.
Заключительные замечания
Существуют и другие алгоритмы генерации случайных чисел, но линейный конгруэнтный метод считается классическим и лёгким для понимания. Если вы хотите глубже изучить данную тему, то обратите внимание на книгу Random Numbers Generators, в которой приведены элегантные доказательства линейного конгруэнтного метода.
Генерация случайных чисел имеет множество приложений в области информатики и особенно важна для криптографии.
Подробно о генераторах случайных и псевдослучайных чисел
Введение
Как отличить случайную последовательность чисел от неслучайной?
Чуть более сложный пример или число Пи

Последовательность цифры в числе Пи считается случайной. Пусть генератор основывается на выводе бит представления числа Пи, начиная с какой-то неизвестной точки. Такой генератор, возможно и пройдет «тест на следующий бит», так как ПИ, видимо, является случайной последовательностью. Однако этот подход не является критографически надежным — если криптоаналитик определит, какой бит числа Пи используется в данный момент, он сможет вычислить и все предшествующие и последующие биты.
Данный пример накладывает ещё одно ограничение на генераторы случайных чисел. Криптоаналитик не должен иметь возможности предсказать работу генератора случайных чисел.
Отличие генератора псевдослучайных чисел (ГПСЧ) от генератора случайных чисел (ГСЧ)
Источники энтропии используются для накопления энтропии с последующим получением из неё начального значения (initial value, seed), необходимого генераторам случайных чисел (ГСЧ) для формирования случайных чисел. ГПСЧ использует единственное начальное значение, откуда и следует его псевдослучайность, а ГСЧ всегда формирует случайное число, имея в начале высококачественную случайную величину, предоставленную различными источниками энтропии.
Энтропия – это мера беспорядка. Информационная энтропия — мера неопределённости или непредсказуемости информации.
Можно сказать, что ГСЧ = ГПСЧ + источник энтропии.
Уязвимости ГПСЧ
Линейный конгруэнтный ГПСЧ (LCPRNG)
Распространённый метод для генерации псевдослучайных чисел, не обладающий криптографической стойкостью. Линейный конгруэнтный метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:
где a (multiplier), c (addend), m (mask) — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа (seed) X0 и при разных его значениях получаются различные последовательности случайных чисел.
Для выбора коэффициентов имеются свойства позволяющие максимизировать длину периода(максимальная длина равна m), то есть момент, с которого генератор зациклится [1].
Пусть генератор выдал несколько случайных чисел X0, X1, X2, X3. Получается система уравнений
Решив эту систему, можно определить коэффициенты a, c, m. Как утверждает википедия [8], эта система имеет решение, но решить самостоятельно или найти решение не получилось. Буду очень признателен за любую помощь в этом направлении.
Предсказание результатов линейно-конгруэнтного метода
Основным алгоритмом предсказания чисел для линейно-конгруэнтного метода является Plumstead’s — алгоритм, реализацию, которого можно найти здесь [4](есть онлайн запуск) и здесь [5]. Описание алгоритма можно найти в [9].
Простая реализация конгруэнтного метода на Java.
Отправив 20 чисел на сайт [4], можно с большой вероятностью получить следующие. Чем больше чисел, тем больше вероятность.
Взлом встроенного генератора случайных чисел в Java
Многие языки программирования, например C(rand), C++(rand) и Java используют LСPRNG. Рассмотрим, как можно провести взлом на примере java.utils.Random. Зайдя в исходный код (jdk1.7) данного класса можно увидеть используемые константы
Метод java.utils.Randon.nextInt() выглядит следующим образом (здесь bits == 32)
Результатом является nextseed сдвинутый вправо на 48-32=16 бит. Данный метод называется truncated-bits, особенно неприятен при black-box, приходится добавлять ещё один цикл в brute-force. Взлом будет происходить методом грубой силы(brute-force).
Пусть мы знаем два подряд сгенерированных числа x1 и x2. Тогда необходимо перебрать 2^16 = 65536 вариантов oldseed и применять к x1 формулу:
до тех пор, пока она не станет равной x2. Код для brute-force может выглядеть так
Вывод данной программы будет примерно таким:
Несложно понять, что мы нашли не самый первый seed, а seed, используемый при генерации второго числа. Для нахождения первоначального seed необходимо провести несколько операций, которые Java использовала для преобразования seed, в обратном порядке.
И теперь в исходном коде заменим
crackingSeed.set(seed);
на
crackingSeed.set(getPreviousSeed(seed));
И всё, мы успешно взломали ГПСЧ в Java.
Взлом ГПСЧ Mersenne twister в PHP
Рассмотрим ещё один не криптостойкий алгоритм генерации псевдослучайных чисел Mersenne Twister. Основные преимущества алгоритма — это скорость генерации и огромный период 2^19937 − 1, На этот раз будем анализировать реализацию алгоритма mt_srand() и mt_rand() в исходном коде php версии 5.4.6.
Можно заметить, что php_mt_reload вызывается при инициализации и после вызова php_mt_rand 624 раза. Начнем взлом с конца, обратим трансформации в конце функции php_mt_rand(). Рассмотрим (s1 ^ (s1 >> 18)). В бинарном представление операция выглядит так:
10110111010111100111111001110010 s1
00000000000000000010110111010111100111111001110010 s1 >> 18
10110111010111100101001110100101 s1 ^ (s1 >> 18)
Видно, что первые 18 бит (выделены жирным) остались без изменений.
Напишем две функции для инвертирования битового сдвига и xor
Тогда код для инвертирования последних строк функции php_mt_rand() будет выглядеть так
Если у нас есть 624 последовательных числа сгенерированных Mersenne Twister, то применив этот алгоритм для этих последовательных чисел, мы получим полное состояние Mersenne Twister, и сможем легко определить каждое последующее значение, запустив php_mt_reload для известного набора значений.
Область для взлома
Если вы думаете, что уже нечего ломать, то Вы глубоко заблуждаетесь. Одним из интересных направлений является генератор случайных чисел Adobe Flash(Action Script 3.0). Его особенностью является закрытость исходного кода и отсутствие задания seed’а. Основной интерес к нему, это использование во многих онлайн-казино и онлайн-покере.
Есть много последовательностей чисел, начиная от курса доллара и заканчивая количеством времени проведенным в пробке каждый день. И найти закономерность в таких данных очень не простая задача.
Задание распределения для генератора псевдослучайных чисел
Для любой случайной величины можно задать распределение. Перенося на пример с картами, можно сделать так, чтобы тузы выпадали чаще, чем девятки. Далее представлены несколько примеров для треугольного распределения и экспоненциального распределения.
Треугольное распределение
Приведем пример генерации случайной величины с треугольным распределением [7] на языке C99.
Экспоненциальное распределение
Тесты ГПСЧ
Некоторые разработчики считают, что если они скроют используемый ими метод генерации или придумают свой, то этого достаточно для защиты. Это очень распространённое заблуждение. Следует помнить, что есть специальные методы и приемы для поиска зависимостей в последовательности чисел.
Одним из известных тестов является тест на следующий бит — тест, служащий для проверки генераторов псевдослучайных чисел на криптостойкость. Тест гласит, что не должно существовать полиномиального алгоритма, который, зная первые k битов случайной последовательности, сможет предсказать k+1 бит с вероятностью большей ½.
В теории криптографии отдельной проблемой является определение того, насколько последовательность чисел или бит, сгенерированных генератором, является случайной. Как правило, для этой цели используются различные статистические тесты, такие как DIEHARD или NIST. Эндрю Яо в 1982 году доказал, что генератор, прошедший «тест на следующий бит», пройдет и любые другие статистические тесты на случайность, выполнимые за полиномиальное время.
В интернете [10] можно пройти тесты DIEHARD и множество других, чтобы определить критостойкость алгоритма.