Что такое смешанная дислокация чему равен ее вектор бюргерса
СМЕШАННЫЕ ДИСЛОКАЦИИ И ИХ ДВИЖЕНИЕ



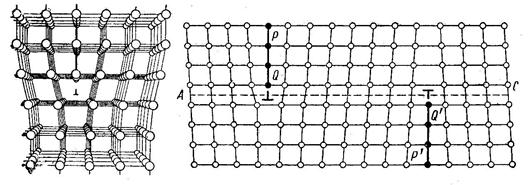
Пунктирные линии соединяют атомы после перемещения (скольжения) винтовой дислокации на один период решетки вправо. Если в исходном положении область несовершенства находилась между атомными рядами 5 и 7, то после смещения на один период
СКОЛЬЖЕНИЕ ВИНТОВОЙ ДИСЛОКАЦИИ
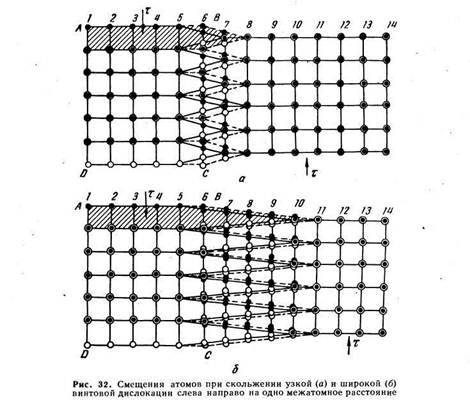
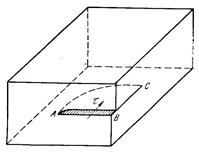
Схема атомного механизма перемещения винтовой дислокации показана на рис. 32. Расположение атомов, соединенных сплошными линиями на рис. 32, а, такое же, как и на рис. 31, а. Плоскость скольжения ABCD совпадает с плоскостью чертежа; черные кружки обозначают атомы под плоскостью чертежа, а белые — над ней. Верхняя стрелка обозначает сдвигающие напряжения, действующие на ту часть кристалла, которая находится над плоскостью чертежа, а нижняя стрелка — напряжения, действующие на часть кристалла под этой плоскостью. Заштрихована ступенька, возникшая при сдвиге на верхней грани кристалла (см. рис. 30). Область несовершенства, внутри которой атомы образуют винтовую лестницу, находится между атомными рядами 5 и 7.
решетки вправо она находится между атомными рядами 6 и 8.Атомы над плоскостью чертежа (белые кружки) под действием сдвигающих напряжений, обозначенных верхней стрелкой, смещаются вниз. Атомы под плоскостью чертежа (черные кружки) под действием сдвигающих напряжений, обозначенных нижней стрелкой, смещаются вверх. Необходимо обратить внимание на три важных обстоятельства. Во-первых, дислокация перемещается на один период решетки вправо в результате передвижений атомов только внутри области несовершенства; атомы вне области несовершенства остаются на своих местах. Во-вторых, дислокация перемещается на один период решетки вследствие передвижения атомов внутри ядра дислокации всего лишь на доли периода решетки. В этом отношении скольжение винтовой дислокации аналогично скольжению краевой дислокации. В-третьих, в области ядра винтовой дислокации атомы смещаются в направлении действующих на них сил (вниз и вверх на рис. 32), а сама дислокация перемещается перпендикулярно этому направлению (вправо на рис. 32). Последнее отличает винтовую дислокацию от краевой; при скольжении краевой дислокации экстраплоскость изменяет свое положение в направлении действующих касательных напряжений.
Перемещение винтовой дислокации увеличило площадь ступеньки и площадь зоны сдвига. В исходном состоянии на рис. 32 зона сдвига, т. е. часть плоскости скольжения, где сдвиг уже совершился, находится между атомными рядами 1 и 5, а после перемещения дислокации вправо на один период решетки зона сдвига находится между атомными рядами 1 и 6.При продвижении винтовой дислокации слева направо на рис. 32 область сдвига постепенно распространяется на всю ширину кристалла.
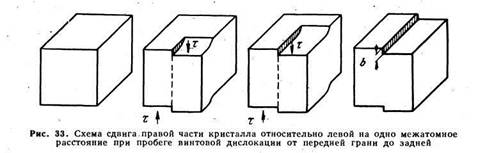
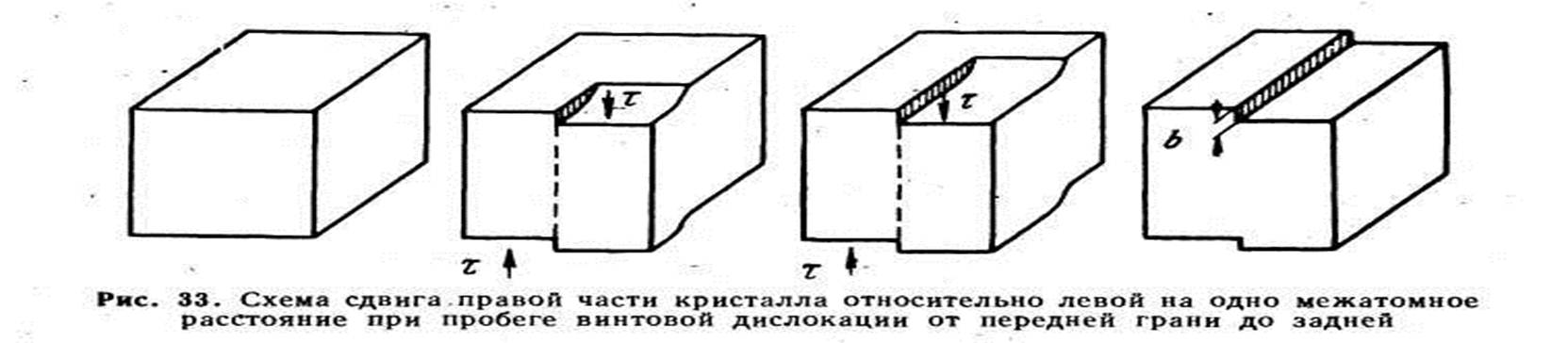
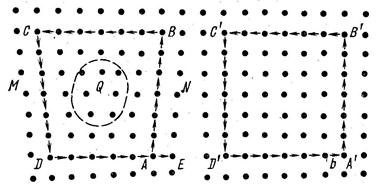
На рис. 33 показан сдвиг на одно межатомное расстояние при пробеге правой винтовой дислокации через весь кристалл от передней грани до задней (сравни с пробегом краевой дислокации на рис. 26).
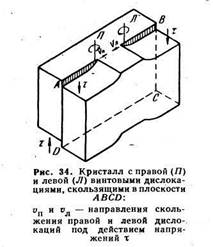
Как видно на рис. 34, под действием одинаковых сдвигающих напряжений винтовые дислокации разного знака скользят в прямо противоположных направлениях.
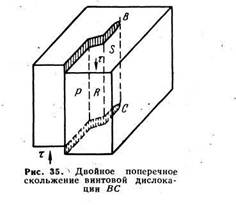
В конце § 12 подчеркивалось, что винтовая дислокация не определяет однозначно плоскость сдвига. Действительно, вокруг линии ВС на рис. 29—31 наблюдается цилиндрическая симметрия искажения решетки. Схемы атомного строения в области дислокации, аналогичные изображенным на рис. 31, а и 32, справедливы не только для плоскостей, параллельных ABCD (см. рис. 29, б и 30), но и для любых вертикальных плоскостей, проходящих через линию ВС на рис. 29, б и 30. Соответственно схема, перемещений атомов на рис. 32, обеспечивающих скольжение винтовой дислокации, также справедлива для любых плоскостей, проходящих через линию ВС на рис. 29, б. Винтовая дислокация в принципе может скользить в любой кристаллографической плоскости, которая содержит линию дислокации и вектор сдвига. В отличие от краевой винтовая дислокация может переходить из одной атомной плоскости в другую без переноса массы — скольжением. Если на пути движения винтовой дислокации в плоскости Р встречается какой-то барьер (см. гл. IX), то дислокация начинает скользить в другой атомной плоскости R, находящейся под углом к первоначальной плоскости скольжения Р (рис. 35). Этот процесс называют поперечным скольжением.
Пройдя некоторый путь в плоскости поперечного скольжения и удалившись от барьера, винтовая дислокация может перейти в атомную плоскость S, параллельную первоначальной плоскости скольжения Р. Этот процесс называют двойным поперечным скольжением. Многократное его повторение называют множественным поперечным скольжением. Например, в г. ц. к. решетке винтовая дислокация, скользившая в плоскости (111), легко переходит в плоскость поперечного скольжения (111), затем вновь скользит в одной из параллельных плоскостей (111), снова совершает поперечное скольжение по плоскости (111) и т.д.
Кроме барьеров, одна из причин поперечного скольжения — изменение вектора приложенных напряжений.
В отличие от краевой винтовая дислокация не может перемещаться с помощью диффузионного механизма, аналогичного приведенному в § 11. Особый случай переползания винтовой дислокации рассмотрен в § 36.
Дислокация не может закончиться внутри кристалла, не соединяясь с другой дислокацией. Это следует из того, что граница зоны сдвига всегда является замкнутой линией. Часть этой границы может проходить по внешней поверхности кристалла. Следовательно, линия дислокации должна замыкаться внутри кристалла или оканчиваться на его поверхности.Здесь возможны самые разнообразные варианты.
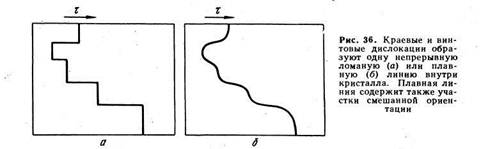
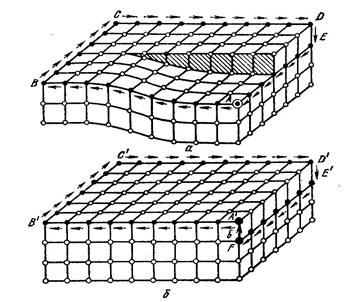
На рис. 36, а линия дислокации состоит из прямых участков краевой и винтовой ориентации, перпендикулярных и параллельных вектору сдвига соответственно. Это частный случай.
В более общем случае в плоскости скольжения линия дислокации является кривой (рис. 36, б).
Отдельные малые участки этой кривой имеют краевую или винтовую ориентацию, но большая ее часть не перпендикулярна и не параллельна вектору сдвига; в последнем случае мы имеем дело с дислокацией смешанной ориентации, которая в макромасштабе является плоской кривой.
15. ВЕКТОР БЮРГЕРСА[2]
Вектор Бюргерса является мерой искаженности кристаллической решетки, обусловленной присутствием в ней дислокации. Он определяет энергию дислокации, действующие на дислокацию силы, величину связанного с дислокацией сдвига, влияет на подвижность дислокации. Следовательно, вектор Бюргерса — главная количественная характеристика дислокации.
Если дислокация вводится в кристалл чистым сдвигом — так, как это было показано выше на примере краевой, винтовой и смешанной дислокаций (см. рис. 22, 29 и 37), то вектор сдвига и является вектором Бюргерса. Вектор сдвига определяет величину и направление смещений атомов в той области, где сдвиг уже произошел, т. е. определяет степень искаженное решетки, связанную с присутствием дислокации, введенной в кристалл путем сдвига. Однако дислокация далеко не всегда вызывается сдвигом. Кроме того, не все типы дислокаций можно определить через вектор сдвига. Поэтому более общим является определение вектора Бюргерса не как вектора сдвига, а как меры искаженность кристаллической решетки.
Чтобы оценить степень искаженности решетки, вызванной дислокацией, следует сравнить несовершенный кристалл, содержащий дислокацию, с совершенным кристаллом. Для этого строят так называемый контур Бюргерса. Контуром Бюргерса называется замкнутый контур произвольной формы, построенный в реальном кристалле путем последовательного обхода дефекта от атома к атому в совершенной области кристалла.
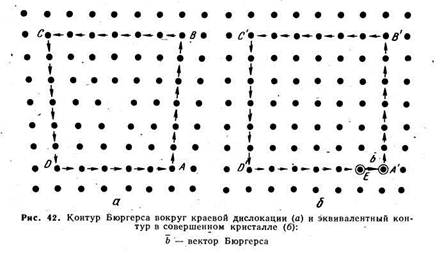
На рис. 42, а показано построение контура Бюргерса вокруг краевой дислокации. За исходную точку принят атом А. Строя контур, пойдем вверх в совершенной области от атома к атому. Пройдя вверх шесть межатомных расстояний, в точке В остановимся и пойдем налево; через шесть межатомных расстояний достигнем точки С и пойдем вниз (мы могли бы по горизонтали справа налево пройти не шесть, а пять, семь или восемь межатомных расстояний). Вниз от точки C, отсчитав шесть межатомных расстояний, попадаем в точку D, находящуюся на одном уровне с точкой A.
Чтобы замкнуть контур на отрезке DA, необходимо пройти не произвольное, а строго определенное число межатомных расстояний — ровно пять. Замкнутая линия ABCD, соединяющая атомы совершенной области решетки и охватывающая краевую дислокацию, является контуром Бюргерса.
Проведем соответствующий контур в совершенном кристалле, т. е. кристалле без дислокации (рис. 42, б). Выберем произвольно в качестве исходной точки атом А’ и пройдем вверх от него шесть межатомных расстояний (до точки В’), затем влево — шесть (до точки С’), вниз — шесть (до точки D’) и вправо — пять межатомных расстояний, т. е. повторим число и направление «шагов», сделанных при построении контура ABCD. Пройдя пять межатомных расстояний вправо от точки D’ мы попадаем в точку Е, а не в исходную точку A’ контур получается незамкнутым. Вектор b, проведенный из точки Е в точку А’ и замыкающий контур, является вектором Бюргерса. Невязка (разомкнутость) контура A’B’C’D’E в совершенном кристалле обусловлена тем, что в кристалле с дислокацией из-за экстраплоскости на стороне ВС, находящейся в верхней половине кристалла, на один атом больше, чем на стороне DA, находящейся в нижней половине кристалла.Вокруг дислокации атомы в совершенной области, где проходит контур Бюргерса ABCD, несколько смещены по сравнению с расположением их в совершенном кристалле без дислокации. Сумма всех упругих смещений, накопившаяся при обходе по контуру Бюргерса ABCD и проявляется в виде невязки, когда соответствующий контур строят в совершенном кристалле.
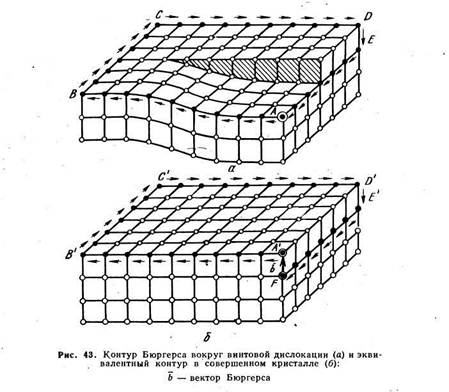
Поэтому вектор Бюргерса, замыкающий в совершенном кристалле контур Бюргерса, является мерой той искаженности решетки в несовершенном кристалле, которая вызвана дислокацией. Величина вектора Бюргерса не зависит от того, насколько контур Бюргерса удален от дислокации. Чем дальше от дислокации мы располагаем этот контур, тем меньше упругие смещения атомов в совершенной области, но тем длиннее контур, и сумма всех упругих смещений, накопившаяся при его обходе, неизменна. Рис. 43 демонстрирует построение контура и вектора Бюргерса для случая винтовой дислокации. Контур Бюргерса можно, например, построить от исходной точки А (рис. 43, а). Пройдем от нее влево девять межатомных расстояний до точки В, шесть — до точки С и вправо девять — до точки D. Чтобы попасть на уровень исходной точки А, спустимся от точки D по вертикали вниз до точки Е на одно межатомное расстояние и пройдем шесть межатомных расстояний от Е до А.
Для проведения соответствующего контура в совершенном кристалле (рис. 43, б) сделаем девять «шагов» от исходной точки А’ до В’, затем шесть — до С, девять — до D’, один шаг вниз по вертикали от D’ до Е’ и шесть шагов — на горизонтальном уровне в сторону исходной точки. При этом мы попадаем не в исходную точку A‘, а в точку F. Невязку контура ликвидируем, замыкая его вектором Бюргерса b (соединяя точки F и A’). Этот вектор на рис. 43, б характеризует степень искаженности решётки, вызванной винтовой дислокацией в кристалле на рис. 43, а. Весьма удобно, что искаженность решетки несовершенного кристалла выражается через период решетки идеального кристалла, т.е. через константу.
Легко увидеть, что векторы Бюргерса, полученные на рис. 42 и 43, являются векторами сдвига.[3]
Направление вектора Бюргерса зависит от направления обхода по контуру Бюргерса. Следовательно, в понятии вектора Бюргерса содержится неопределенность, соответствующая углу в 180 град. Но это не является серьезным недостатком, так как сущность указанной неопределенности сводится к тому, например, что пробег краевой дислокации через весь кристалл (см. рис. 26) вызвал сдвиг верхней половины кристалла влево относительно нижней или, что то же самое, сдвиг нижней половины кристалла вправо относительно верхней половины.
Вектор Бюргерса характеризуется рядом особенностей:
Лекция 5. Основные типы дислокаций: краевые, винтовые и смешанные дислокации



Основные типы дислокаций: краевые, винтовые и смешанные дислокации. Вектор Бюргерса. Перемещение дислокаций скольжением и переползанием.
Дислокации принадлежат к линейным несовершенствам кристалла. Первоначально представления о дислокации были введены в физику твёрдого тела в 1934 году для того, чтобы объяснить несоответствие между наблюдаемой и теоретической прочностью и описать атомный механизм скольжения при пластической деформации кристаллов. Численные теоретические значения скалывающих напряжений, необходимых для деформации оказываются больше экспериментальных в 10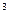
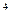
Схема краевой дислокации показана на рис.20. Если в кристалле сделать надрез по плоскости АВСД и сдвинуть части кристалла вдоль плоскости надреза, перпендикулярно к краю надреза, что полученная граница АВ между участком, где скольжение уже произошло, и ненарушенным участком будет краевой дислокацией (рис.20.а). Представим себе, что в части кристалла по каким либо причинам появилась лишняя полуплоскость атомов, так называемая экстраплоскость. Вблизи края экстраплоскости решётка сильно искажена. В этом участке кристаллов против n атомов одного ряда располагается n+1 или n-1 атомов другого ряда. Выше края экстраплоскости (линия АВ) межатомные расстояния меньше параметра решётки, а ниже края – больше. Атом на самой кромке экстраплоскости имеет меньше соседей, чем внутри совершенной решётки. Таким образом, вдоль края экстраплоскости находится область с несовершенной решёткой, которая называется краевой дислокацией.
Рисунок 20 – Краевая дислокация
а – пространственная схема,
б – схема расположения атомов в области дислокации
Ядром или центром дислокации называют осевую зону дефектного участка кристалла, где очень сильны искажения решётки. Положение ядра дислокации в кристаллографической плоскости, являющейся плоскостью чертежа, обозначается знаком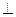
Большое значение в теории прочности и пластичности металлов имеет характер искажений кристаллической решётки вокруг краевой дислокации. У положительной краевой дислокации наблюдается растяжение кристаллической решётки под плоскостью скольжения, выше плоскости – сжатие решётки. У отрицательной дислокации наоборот.
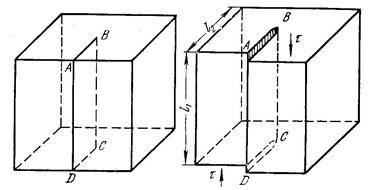
Рисунок 21 – Сдвиг, создавший винтовую дислокацию.
а – кристалл до сдвига надрезан по АВСD, б – кристалл после сдвига, АВСD – зона сдвига.
Дислокации смешанной ориентации наиболее распространены в металлах и сплавах. Зона сдвига АВС на рис.22 ограничена линией дислокации АС. Плоскость чертежа является плоскостью скольжения, чёрные кружки обозначают атомы, расположенные под плоскостью скольжения, белые – над ней. Вблизи точки А дислокация имеет винтовую ориентацию, около точки В – краевую. Линия смешанной дислокации может оканчиваться на гранях кристалла, как это показано на рис.22, кроме того, возможно существование замкнутой петли внутри кристалла. Отдельные участки имеют чисто винтовую или краевую ориентацию, но, в основном, ориентация дислокаций смешанная. Петля определяет границу зоны сдвига части кристалла (внутри петли) относительно области вне петли, не претерпевшей сдвиг.
Рисунок 22 – дислокация смешанной
Дислокации, находящиеся в кристаллической решётке зёрен и кристаллов, называют дислокациями решётки, или внутризеренными.
Геометрически дислокации характеризуются двумя параметрами: направлением линии дислокации и вектором Бюргерса (рис.23).
Рисунок 23 – схема определения вектора Бюргерса
а – схема плоскости реального кристалла,
б – решётка совершенного кристалла.
Вектор Бюргерса является мерой искаженности кристаллической решётки, обусловленной присутствием в ней дислокации. Он определяет энергию дислокации, действующие на дислокации силы, величину, связанного с дислокацией сдвига, влияет на подвижность дислокации. Следовательно вектор Бюргерса главная количественная характеристика дислокации.
Если дислокация вводится в кристалл чистым сдвигом – так как это было показано ранее на примере краевой, винтовой дислокации, то вектор сдвига и является вектором Бюргерса. Вектор сдвига определяет величину и направление смещения атомов в той области, где сдвиг уже произошел, т.е. определяет степень искаженности решётки, связанную с присутствием дислокации, введенной в кристалл путём сдвига. Однако дислокация не всегда называется сдвигом. Кроме того, не все типы дислокаций можно определять через вектор сдвига. Поэтому более общим является определение вектора Бюргерса не как сдвига, а как меры искаженности кристаллической решётки.
Чтобы оценить степень искаженности кристаллической решётки, вызванной дислокацией, следует сравнить несовершенный кристалл, содержащий дислокацию, с совершенным кристаллом. Для этого строят так называемый контур Бюргерса. Контуром Бюргерса называется замкнутый контур произвольной формы, построенный в реальном кристалле путём последовательного обхода дефекта от атома к атому в совершенной области кристалла.
При одинаковом количестве шагов в горизонтальном и вертикальном направлении в конце концов приходим к первоначальному атому, т.е. в идеальном кристалле контур Бюргерса замкнут. В кристалле, содержащем краевую положительную дислокацию, контур Бюргерса окажется незамкнутым. Остаётся ещё отрезок, длина и направление которого определяют вектор Бюргерса.
На рис.24 показано построение контура и вектора Бюргерса для винтовой дислокации. Контур Бюргерса можно, например, построить от исходной точки А (рис.24.а). Пройдём от неё влево девять межатомных расстояний до точки В, шесть до точки С и вправо девять до точки Д. Чтобы попасть на уровень исходной точки А, опустимся от точки Д по вертикали вниз до точки Е на одно межатомное расстояние и пройдём шесть межатомных расстояний от Е доА.
Рисунок 24 – Контур Бюргерса вокруг винтовой дислокации (а) и эквивалентный контур в совершенном кристалле (б)
Для проведения соответствующего контура к совершенном кристалле (рис 24.б) сделаем девять шагов от исходной точки А







Дислокации, у которых вектор Бюргерса соответствует тождественной трансляции атома, называются полными или единичными. Векторы единичных дислокаций имеют в решётке различные направления. Энергия дислокаций будет минимальной в том случае, когда их векторы Бюргерса параллельны направлению плотнейшей упаковки атомов в кристаллической решётке. Частичными являются такие дислокации, вектор Бюргерса не соответствует тождественной трансляции атома. Векторы Бюргерса частичных дислокаций меньше, чем полных.
Вектор Бюргерса характеризуется рядом особенностей:
1. Нормален к лини краевой дислокации и параллелен к линии винтовой дислокации. Вдоль линии смешанной дислокации угол между ней и вектором Бюргерса в разных точках имеет разную величину и располагается под углом к линии дислокации АС.
2. У дефектов недислокационного типа равен нулю. Если построить контур Бюргерса вокруг любого точечного или линейного дефекта недислокационного типа (вокруг цепочки атомов или вакансий), то соответствующий контур в идеальном кристалле окажется замкнутым.
3. Одинаков вдоль всей линии дислокации, т.е. является инвариантом дислокации. Это следует, например, из того, что при смещении контура Бюргерса вдоль линии дислокации он всё равно будет оставаться эквивалентным исходному контуру (при условии, что он всеми своими точками не выходит из совершенной области решётки, т.е. не пересекает другие несовершенства). Кроме того, вектор сдвига, создающего, например, криволинейную смешанную дислокацию, имеет одну величину и одно направление для всего кристалла.
Из инвариантности вектора Бюргерса вытекает важное следствие: дислокация не может обрываться внутри кристалла. Внутри кристалла дислокации могут образовывать замкнутые петли с одинаковыми векторами Бюргерса вдоль всей петли или встречаться с другими дислокациями, образовывая узлы (точки встречи).
Выход дислокаций на поверхность шлифа металла проявляется в виде точки – углубления. Дислокации являются местами развития растущего кристалла. Эти же места активны при обратном процессе – растворении.
К параметрам, характеризующим свойства дислокации относятся её длина и ширина. Длина дислокации – это протяженность зоны искажения кристаллической решётки. В чистых ГЦК металлах устойчивая дислокация при напряжениях, сравнимых с пределом текучести, может иметь длину 10-3 – 10-4 см. Под шириной краевой дислокации следует понимать ширину области на плоскости скольжения, где величина межатомных смещений составляет не менее 1/8 максимального значения атомного смещения в центре дислокации, равного примерно 1/4а. Ширина дислокации определяет её энергию, подвижность, уровень напряжений, при которых дислокация может двигаться вдоль плоскости скольжения.