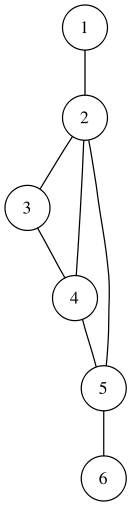
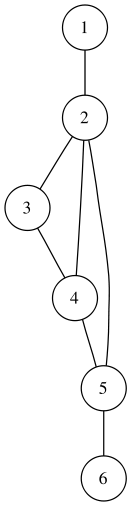
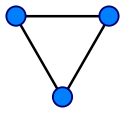
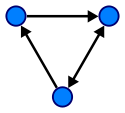
Что такое смешанный граф
Основные виды графов
Виды графов могут определяться общими принципами их построения (таковы, например, двудольный граф и эйлеров граф), а могут зависеть от тех или иных свойств вершин или рёбер (например, ориентированный и неориентированный граф, обыкновенный граф).
Ориентированные и неориентированные графы
Графы, в которых все рёбра являются звеньями (порядок двух концов ребра графа не существенен), называются неориентированными.
Графы, в которых все рёбра являются дугами (порядок двух концов ребра графа существенен), называются ориентированными графами или орграфами.
Неориентированный граф может быть представлен в виде ориентированного графа, если каждое его звено заменить на две дуги, имеющие противоположные направления.
Графы с петлями, смешанные графы, пустые графы, мультиграфы, обыкновенные графы, полные графы
Если граф содержит петли, то это обстоятельство специально оговаривают, добавляя к основной харатеристике графа слова «с петлями», например, «орграф с петлями». Если граф не содержит петель, то добавляют слова «без петель».
Смешанным называют граф, в котором имеются рёбра хотя бы двух из упомянутых трёх разновидностей (звенья, дуги, петли).
Граф, состоящий только из голых вершин, называется пустым.
Мультиграфом называется граф, в котором пары вершин могут быть соединены более чем одним ребром, то есть содершащий кратные рёбра, но не содержащий петель.
Граф без дуг (то есть неориентированный), без петель и кратных рёбер называется обыкновенным. Обыкновенный граф изображён на рисунке ниже.
Граф заданного типа называют полным, если он содержит все возможные для этого типа рёбра (при неизменном множестве вершин). Так, в полном обыкновенном графе каждая пара различных вершин соединена ровно одним звеном (рисунок ниже).
Двудольный граф
Граф называется двудольным, если множество его вершин можно разбить на два подмножества так, чтобы никакое ребро не соединяло вершины одного и того же подмножества.
Пример 1. Построить полный двудольный граф.
Полный двудольный граф состоит из двух множеств вершин и из всевозможных звеньев, соединяющих вершины одного множества с вершинами другого множества (рисунок ниже).
Эйлеров граф
Мы уже касались задачи о кёнигсбергских мостах. Отрицательное решение Эйлером этой задачи привело к первой опубликованной работе по теории графов. Задачу об обходе мостов можно обобщить и получить следующую задачу теории графов: можно ли найти в данной графе цикл, содержащий все вершины и все рёбра? Граф, в котором это возможно, называется эйлеровым графом.
Итак, эйлеровым графом называется граф, в котором можно обойти все вершины и при этом пройти одно ребро только один раз. В нём каждая вершина должна иметь только чётное число рёбер.
Пример 2. Является ли полный граф с одинаковым числом n рёбер, которым инцидентна каждая вершина, эйлеровым графом? Объяснить ответ. Привести примеры.
Регулярный граф
Регулярным графом называется связный граф, все вершины которого имеют одинаковую степень k. Таким образом, на рисунке к примеру 2 изображены примеры регулярных графов, называемых по степени его вершин 4-регулярными и 2-регулярными графами или регулярными графами 4-й степени и 2-й степени.
Число вершин регулярного графа k-й степени не может быть меньше k+1. У регулярного графа нечётной степени может быть лишь чётное число вершин.
Пример 3. Построить регулярный граф, в котором самый короткий цикл имеет длину 4.
Решение. Рассуждаем так: для того, чтобы длина цикла удовлетворяла заданному условию, требуется, чтобы число вершин графа было кратно четырём. Если число вершин равно четырём, то получится граф, изображённый на рисунке ниже. Он является регулярным, но в нём самый короткий цикл имеет длину 3.
Увеличиваем число вершин до восьми (следующее число, кратное четырём). Соединяем вершины рёбрами так, чтобы степени вершин были равны трём. Получаем следующий граф, удовлетворяющий условиям задачи.
Гамильтонов граф
Взвешенный граф
Графы-деревья
Деревом называется связный граф без циклов (рисунок ниже). Любые две вершины дерева соединены лишь одним маршрутом.
Число q рёбер графа находится из соотношения
Приведённое соотношение выражает критическое значение числа рёбер дерева, так как, если мы присоединим к дереву ещё одно ребро, то будет создан цикл, а если уберём одно ребро, то граф-дерево разделится на две компоненты. Граф, состоящий из компонент дерева, называется лесом.
В виде графов, особенно в виде деревьев, строятся многие математические модели, о которых также можно узнать на нашем сайте.
Граф (теория графов)
В математической теории графов и информатике граф — это совокупность объектов со связями между ними.
Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.
Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами. Например, строение Википедии можно смоделировать при помощи ориентированного графа (орграф), в котором вершины — это статьи, а дуги (ориентированные рёбра) — это связи, созданные гиперссылками (см. Тематическая карта).
Содержание
Определения
Теория графов не обладает устоявшейся терминологией. В различных статьях под одними и теми же терминами понимаются разные вещи. Приводимые ниже определения — наиболее часто встречаемые.
V (а значит и E ) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становятся ложными в случае бесконечных множеств.
Вершины и рёбра графа называются также элементами графа, число вершин в графе | V | — порядком, число рёбер | E | — размером графа.
Два ребра называются смежными, если они имеют общую концевую вершину.
Два ребра называются кратными, если множества их концевых вершин совпадают.
Степенью degV вершины V называют количество рёбер, для которых она является концевой (при этом петли считают дважды).
Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.
Ориентированный граф
Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга v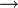 
w ведёт от вершины v к вершине w.
Смешанный граф
Понятно, что ориентированный и неориентированный графы являются частными случаями смешанного.
Прочие связанные определения
Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.
Ориентированным путём в орграфе называют конечную последовательность вершин vi 
, для которой все пары (vi,vi + 1) 
являются (ориентированными) рёбрами.
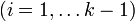
Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины u и v являются концами некоторого ребра, то согласно данному определению, последовательность (u,v,u) является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.
Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что:
Бинарное отношение на множестве вершин графа, заданное как «существует путь из u в v », является отношением эквивалентности, и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.
Всякий максимальный связный подграф графа G называется связной компонентой (или просто компонентой) графа G. Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов
Ребро графа называется мостом, если его удаление увеличивает число компонент.
Дополнительные характеристики графов
Способы представления графа в информатике
Матрица смежности
Матрица смежности — таблица, где как столбцы, так и строки соответствуют вершинам графа. В каждой ячейке этой матрицы записывается число, определяющее наличие связи от вершины-строки к вершине-столбцу (либо наоборот).
Недостатком являются требования к памяти — очевидно, квадрат количества вершин.
Матрица инцидентности
Данный способ является самым ёмким (размер пропорционален | E | | V | ) и неудобным для хранения, но облегчает нахождение циклов в графе.
Список рёбер
Список рёбер — это тип представления графа в памяти, подразумевающий, что каждое ребро представляется двумя числами — номерами вершин этого ребра. Список рёбер более удобен для реализации различных алгоритмов на графах по сравнению с матрицей смежности.
Обобщение понятия графа
Простой граф является одномерным симплициальным комплексом.
Более абстрактно, граф можно задать как тройку 
, где V и E — некоторые множества (вершин и рёбер, соотв.), а 
— функция инцидентности (или инцидентор), сопоставляющая каждому ребру 
(упорядоченную или неупорядоченную) пару вершин u и v из V (его концов). Частными случаями этого понятия являются:
Под данное выше определение не подходят некоторые другие обобщения:
Литература
См. также
Ссылки
Популярные программы для визуализации графов
Граф (математика)
В математической теории графов и информатике граф — это совокупность непустого множества вершин и множества пар вершин (связей между вершинами).
Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.
Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами. Например, строение Википедии можно смоделировать при помощи ориентированного графа (орграф), в котором вершины — это статьи, а дуги (ориентированные рёбра) — гиперссылки (см. Тематическая карта).
Содержание
Определения
Теория графов не обладает устоявшейся терминологией. В различных статьях под одними и теми же терминами понимаются разные вещи. Ниже приведены наиболее часто встречаемые определения.
Граф, или неориентированный граф 
— это упорядоченная пара 
, для которой выполнены следующие условия:
(а значит и, 
, иначе оно было бы мультимножеством) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становится ложным в случае бесконечных множеств.
Вершины и рёбра графа называются также элементами графа, число вершин в графе 
— порядком, число рёбер 
— размером графа.
Вершины 
и 
называются концевыми вершинами (или просто концами) ребра 
. Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.
Два ребра называются смежными, если они имеют общую концевую вершину.
Два ребра называются кратными, если множества их концевых вершин совпадают.
Ребро называется петлёй, если его концы совпадают, то есть 
.
Степенью 
вершины называют количество инцидентных ей рёбер (при этом петли считают дважды).
Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.
Ориентированный граф
Ориентированный граф (сокращённо орграф) — это упорядоченная пара 
, для которой выполнены следующие условия:
Дуга — это упорядоченная пара вершин 
, где вершину называют началом, а 
— концом дуги. Можно сказать, что дуга 
ведёт от вершины к вершине .
Смешанный граф
Смешанный граф — это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые — неориентированными. Записывается упорядоченной тройкой 
, где , и 
определены так же, как выше.
Ориентированный и неориентированный графы являются частными случаями смешанного.
Изоморфные графы
Граф называется изоморфным графу 
, если существует биекция 
из множества вершин графа в множество вершин графа , обладающая следующим свойством: если в графе есть ребро из вершины в вершину 
, то в графе должно быть ребро из вершины 
в вершину 
и наоборот — если в графе есть ребро из вершины в вершину , то в графе должно быть ребро из вершины 
в вершину 
. В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.
Прочие связанные определения
Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.
Ориентированным путём в орграфе называют конечную последовательность вершин 
, для которой все пары 
являются (ориентированными) рёбрами.
Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины и являются концами некоторого ребра, то согласно данному определению, последовательность 
является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.
Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что:
Бинарное отношение на множестве вершин графа, заданное как «существует путь из в », является отношением эквивалентности и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.
Всякий максимальный связный подграф графа G называется связной компонентой (или просто компонентой) графа . Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов
Ребро графа называется мостом, если его удаление увеличивает число компонент.
Дополнительные характеристики графов
Обобщение понятия графа
Простой граф является одномерным симплициальным комплексом.
Более абстрактно, граф можно задать как тройку 
, где и — некоторые множества (вершин и рёбер, соотв.), а 
— функция инцидентности (или инцидентор), сопоставляющая каждому ребру 
(упорядоченную или неупорядоченную) пару вершин и из (его концов). Частными случаями этого понятия являются:
Под данное выше определение не подходят некоторые другие обобщения:
Способы представления графа в информатике
Матрица смежности
Таблица, где как столбцы, так и строки соответствуют вершинам графа. В каждой ячейке этой матрицы записывается число, определяющее наличие связи от вершины-строки к вершине-столбцу (либо наоборот).
Недостатком являются требования к памяти, прямо пропорциональные квадрату количества вершин.
Матрица инцидентности
Каждая строка соответствует определённой вершине графа, а столбцы соответствуют связям графа. В ячейку на пересечении 
-ой строки с 
-м столбцом матрицы записывается:
1 в случае, если связь «выходит» из вершины , −1, если связь «входит» в вершину, 0 во всех остальных случаях (то есть если связь является петлёй или связь не инцидентна вершине)
Данный способ является самым ёмким (размер пропорционален 
) для хранения, но облегчает нахождение циклов в графе.
Список рёбер
Список рёбер — это тип представления графа, подразумевающий, что каждое ребро представляется двумя числами — номерами вершин этого ребра.
Языки описания и программы построения графов
Для описания графов в целях, пригодных для машинной обработки и одновременно удобном для человеческого восприятия используется несколько стандартизированных языков, среди которых:
Отметим специализированные коммерческие программы для построения графов:
Из бесплатных можно отметить:
Для визуализации графов можно использовать:
См. также
Литература
Полезное
Смотреть что такое «Граф (математика)» в других словарях:
Граф — Граф: От древневерхненемецкого gravo, gravio «предводитель, вождь»: Граф (титул) дворянский титул; «Граф» короткометражная немая кинокомедия Чарли Чаплина (The Count, 1916). От греч. γράφω «царапаю, черчу, пишу»: Граф… … Википедия
Граф зависимостей — В математике, информатике и цифровой электронике, граф зависимостей представляет собой ориентированный граф, отражающий зависимости нескольких объектов друг к другу. По графу зависимостей можно определить порядок вычислений или его недостатки,… … Википедия
Граф объектный — это совокупность узлов и ребер, соединяющих эти узлы. Объектные графы обеспечивают простой способ учета взаимных связей в множестве объектов, и не обязательно, чтобы эти связи в точности проецировались в классические связки объектно… … Википедия
Граф Келли (теория групп) — Граф Кэли граф, который строится по группе с выделенной системой образующих. Назван в честь английского математика Артура Кэли (A. Cayley). Определение Пусть дана дискретная группа G и система образующих S. Предположим S = S − 1, то есть, для… … Википедия
Граф Петерсена — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей … Википедия
ГРАФ СЛУЧАЙНЫЙ — вероятностная модель, предназначенная для изучения частотных характеристик различных параметров графов. Под Г. с. обычно понимается нек рый класс графов на к ром задано распределение вероятностей. Произвольный конкретный граф Gиз наз. реализацией … Математическая энциклопедия
Граф — Антон (Graf, Anton) 1736, Винтертур 1813, Дрезден. Немецкий живописец. Учился в 1753 1756 у И. У. Шелленберга в Винтертуре, затем у И. Я. Хайда в Аугсбурге. Работал как портретист в Регенсбурге, Винтертуре, Аугсбурге, Мюнхене, Цюрихе. С 1766… … Европейское искусство: Живопись. Скульптура. Графика: Энциклопедия
Объектный граф — Граф объектный это совокупность узлов и ребер, соединяющих эти узлы. Объектные графы обеспечивают простой способ учёта взаимных связей в множестве объектов, и не обязательно, чтобы эти связи в точности проецировались в классические связки… … Википедия
Гамильтонов граф — Граф додекаэдра с выделенным циклом Гамильтона … Википедия
Планарный граф — Планарный граф граф, который может быть изображен на плоскости без пересечения ребер. Более строго: Граф укладывается на некоторой поверхности, если его можно на ней нарисовать без пересечения ребер. Уложенный граф называется геометрическим … Википедия