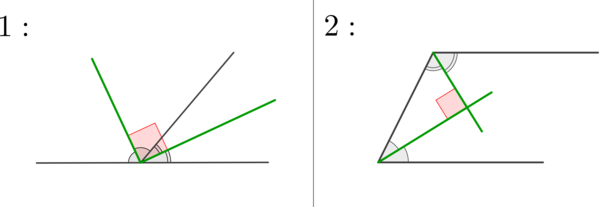
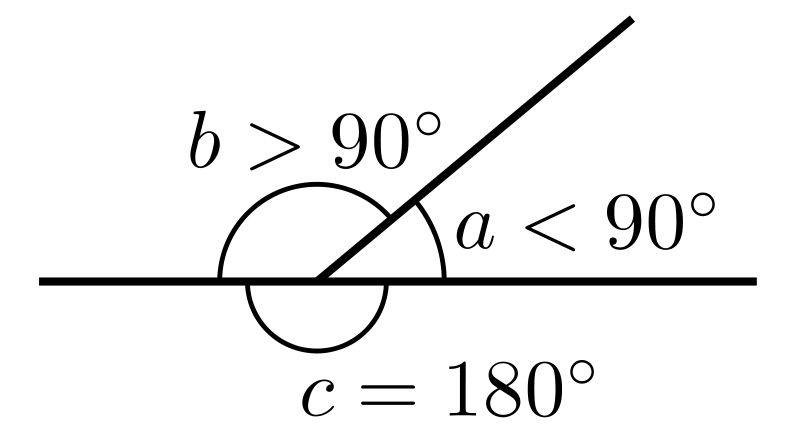Что такое смешанный угол
Смежные углы
Что такое смежные углы? Какие у них свойства?
Определение.
Смежные углы — это углы, у которых одна сторона — общая, а другие стороны лежат на одной прямой.
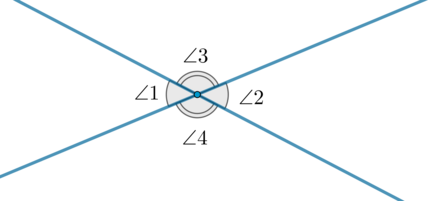
∠1 и ∠2 — смежные углы
Сколько смежных углов образуется при пересечении двух прямых?
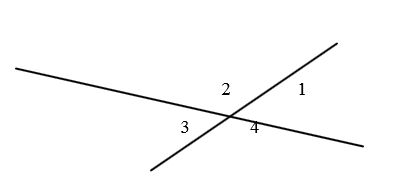
При пересечении двух прямых образуется четыре пары смежных углов:
Но, так как ∠1 =∠4, ∠2=∠3 (как вертикальные), то достаточно рассмотреть только одну из этих пар.
Свойство смежных углов.
Сумма смежных углов равна 180º.
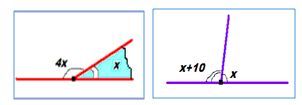
1) Даны два смежных угла. Один на 42 градуса больше другого. Найти эти углы.
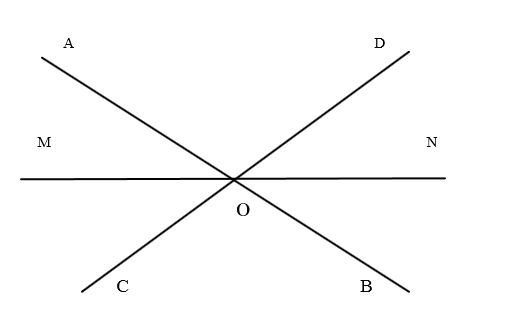
∠AOC и ∠BOC — смежные,
∠AOC на 42º больше, чем ∠BOC
Пусть ∠BOC=хº, тогда ∠AOC= х+42º. Так как сумма смежных углов равна 180º, то ∠BOC+∠AOC=180º.
Значит, ∠BOC= 69º, ∠AOC=69+42=111º.
2) Найти смежные углы, если их градусные меры относятся как 4:5.
Значит, смежные углы равны 4∙20=80º и 5∙20=100º.
3) Один из углов, образованных при пересечении двух прямых, в 5 раз больше другого. Найти эти углы.
Дано: AB и CD — прямые, O — точка их пересечения,
∠AOD в 5 раз больше, чем ∠BOD
При пересечении двух прямых образуются смежные и вертикальные углы. Так как вертикальные углы равны между собой, то углы∠AOD и ∠BOD — смежные. Пусть ∠BOD=xº, тогда ∠AOD=5xº. Так как сумма смежных углов равна 180º, ∠AOD +∠BOD=180º.
Значит, ∠BOD=30º, ∠AOD=5∙30=150º.
Могут ли смежные углы быть равными?
Да. Если смежные углы равны между собой, то, так как сумма смежных углов равна 180º, каждый из них равен половине суммы, то есть 90º.
угол, смежный с прямым, есть прямой угол.
Могут ли два смежных угла быть тупыми? Острыми?
Нет. Так как градусная мера тупого угла больше 90º, то сумма двух тупых углов больше 180º. А сумма смежных углов равна 180º.
Градусная мера острого угла меньше 90º. Значит, сумма двух острых углов меньше 180º.
Таким образом, в паре смежных углов один — тупой, другой — острый (или оба прямые).
Углы. Смежные углы.
Какие углы называются смежными?
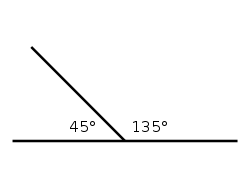
Смежными углами называется пара углов с общей вершиной и одной
общей стороной. 2 оставшиеся стороны делают продолжение друг
другу, образовывая прямую линию. Для угла 135 градусов смежным
будет угол равный 45 градусам. Для угла x градусов смежным
является угол (180 – x) градусов.

Два смежных угла — это углы, с одной общей стороной, а остальные стороны находятся на одной прямой.
При пересечении 2-х прямых получается 4-ре пары смежных углов:
Но, так как ∠1 =∠4, ∠2 = ∠3 (как вертикальные), то достаточно рассматривать
только одну из этих пар.

Свойство смежных углов.
Чему равна сумма смежных углов?
Смежные углы равны: сумма смежных углов 180º.
Следствия из теоремы о смежных углах.
Тригонометрические соотношения.
противоположные знаки (исключение неопределенные значения).
Задание. Чему будет равна градусная мера угла α, когда градусная мера смежного ему угла = 70°?
Как найти смежный угол?
Решение. Из теоремы о смежных углах находим:
Смежные углы
Тригонометрические соотношения
Синусы смежных углов равны. Их косинусы и тангенсы равны по величине, но имеют противоположные знаки (за исключением неопределённых значений).
См. также
Ссылки
Полезное
Смотреть что такое «Смежные углы» в других словарях:
Смежные углы — углы, у которых одна сторона общая, а другие стороны лежат на одной прямой (на рис. углы 1 и 2 смежные). Рис. к ст. Смежные углы … Большая советская энциклопедия
СМЕЖНЫЕ УГЛЫ — углы, имеющие общую вершину и одну общую сторону, а две др. их стороны лежат на одной прямой … Большая политехническая энциклопедия
СМЕЖНЫЕ УГЛЫ — см. Угол … Большой Энциклопедический словарь
СМЕЖНЫЕ УГЛЫ — СМЕЖНЫЕ УГЛЫ, два угла, сумма которых равна 180°. Каждый из этих углов дополняет другой до развернутого угла … Научно-технический энциклопедический словарь
смежные углы — см. Угол. * * * СМЕЖНЫЕ УГЛЫ СМЕЖНЫЕ УГЛЫ, см. Угол (см. УГОЛ) … Энциклопедический словарь
Смежные углы — (Angles adjacents) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие С. углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через вершину … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
СМЕЖНЫЕ УГЛЫ — см. Угол … Естествознание. Энциклопедический словарь
Вертикальные углы — Две прямые пересекаются, создавая пару вертикальных углов. Одна пара состоит из углов A и B, другая из C и D. В геометрии, два угла называются вертикальными, если они созданы пересечением двух … Википедия
Комплементарные углы — Пара комплементарных углов, дополняющих друг друга до 90 градусов Комплементарные углы это пара углов, которые дополняют друг друга до 90 градусов. Если два комплементарных угла являются соседними (т.е. имеют общую вершину и разделяются только… … Википедия
Дополнительные углы — Пара дополнительных углов, дополняющих друг друга до 90 градусов Дополнительные углы это пара углов, которые дополняют друг друга до 90 градусов. Если два дополнительных угла являются с … Википедия
Что такое смешанный угол
Угол – это геометрическая фигура ( рис.1 ), образованная двумя лучами OA и OB ( стороны угла ), исходящими из одной точки O ( вершина угла ).
СМЕЖНЫЕ УГЛЫ — два угла, сумма которых равна 180°. Каждый из этих углов дополняет другой до развернутого угла.
Смежные углы — (Agles adjacets) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
На рисунке 2 углы a1b и a2b смежные. У них общая сторона b, а стороны a1, a2 — дополнительные полупрямые.
На рисунке 3 изображена прямая AB, точка C расположена между точками A и B. Точка D — точка не лежащая на прямой AB. Получается, что углы BCD и ACD смежные. У них общая сторона CD, а стороны CA и CB дополнительные полупрямые прямой AB, так как точки A, B разделены начальной точкой C.
Теорема о смежных углах
Теорема: сумма смежных углов равна 180°
Доказательство:
Углы a1b и a2b смежные (см. рис. 2) Луч b проходит между сторонами a1, и a2 развернутого угла. Следовательно, сумма углов a1b и a2b равна развернутому углу, то есть 180°. Теорема доказана.
Угол, равный 90° называется прямым. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом также прямой угол. Угол, меньший 90° называется острым, а угол больше 90° — тупым. Так как сумма смежных углов равна 180°, значит угол, смежный с острым углом — тупой угол. А угол смежный с тупым углом — острый угол.
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.
Определение 1. Углом называется часть плоскости, ограниченная двумя лучами с общим началом.
Определение 2. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым.
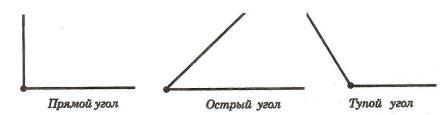
Определение 4. Угол, меньший 90 градусов, называется острым углом.
Определение 5. Угол, больший 90 градусов и меньший 180 градусов, называется тупым углом.
пересекающиеся прямые.
Определение 6. Два угла, одна сторона которых общая, а другие стороны лежат на одной прямой, называются смежными.
Определение 7. Углы, стороны которых продолжают друг друга, называются вертикальными углами.
На рисунке 1:
смежные: 1 и 2; 2 и 3; 3 и 4; 4 и 1
вертикальные: 1 и 3; 2 и 4
Теорема 1. Сумма смежных углов равна 180 градусов.
Для доказательства рассмотрим на рис. 4 смежные углы АОВ и ВОС. Их суммой является развернутый угол АОС. Поэтому сумма данных смежных углов равна 180 градусов.
Интересный факт
Связь математики с музыкой
Так же предложу вашему внимаю забавную пародию про спор двух математиков =)
Геометрия вокруг нас
Геометрия в нашей жизни имеет немаловажное значение. Ввиду того, что когда оглядеться вокруг, то не сложно будет заметить, что нас окружают различные геометрические фигуры. Мы с ними сталкиваемся повсюду: на улице, в классе, дома, в парке, в спортивном зале, в школьной столовой, в принципе везде, где бы мы с вами не находились. Но темой сегодняшнего урока являются смежные угли. Поэтому давайте оглянемся вокруг и попытаемся в этом окружении найти углы. Если вы внимательно посмотрите в окно, то можете увидеть, что некоторые ветки дерева образуют смежные углы, а в перегородках на воротах можно заметить множество вертикальных углов. Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке.
1. Вот на столе на книжной подставке стоит книга. Какой угол она образует?
2. А вот ученик работает за ноутбуком. Какой угол вы видите здесь?
3. Какой угол образует фото рамка на подставке?
4. Как вы думаете, возможно ли, чтобы два смежных угла были равными?
Перед вами изображена геометрическая фигура. Что это за фигура, назовите ее? А теперь назовите все смежные углы, которые вы можете увидеть на этой геометрической фигуре.
Перед вами изображение рисунка и картины. Рассмотрите их внимательно и скажите, какие виды улов вы видите на картине, а какие углы на рисунке.
Решение задач
Математический диктант на повторение ранее выученного материала
1. Может ли сумма 3-х углов, образованных при пересечении 2-х прямых, равняться 100°? 370°?
2. На рисунке найдите все пары смежных углов. А теперь вертикальных углов. Назовите эти углы.
3. Нужно найти угол, когда он втрое больше, чем смежный с ним.
4. Две прямые пересеклись между собой. В результате этого пересечения образовались четыре угла. Определите величину любого из них, при условии что:
а) сумма 2-х углов из четырех 84°;
б) разность 2-х углов из них равна 45°;
в) один угол в 4 раза меньше чем второй;
г) сумма трех из данных углов равна 290°.
Итог урока
1. назовите углы, которые образуются при пересечении 2-х прямых?
2. Назовите все возможные пары углов, находящихся на рисунке, и определите их вид.
1. Найдите отношение градусных мер смежных углов, когда один из них на 54° больше второго.
2. Найдите углы, которые образуются при пересечении 2-х прямых, при условии, что один из углов равняется сумме 2-х других углов, смежных с ним.
3. Необходимо найти смежные углы, когда биссектриса одного из них образует со стороной второго угол, который больше чем второй угол на 60°.
4. Разница 2-х смежных углов равна трети от суммы этих двух углов. Определите величины 2-х смежных углов.
5. Разница и сумма 2-х смежных углов относятся как 1 : 5 соответственно. Найдите смежные углы.
6. Разница двух смежных составляет 25% от их суммы. Как относятся величины 2-х смежных углов? Определите величины 2-х смежных углов.
Смежные и вертикальные углы. Треугольник. Равнобедренный треугольник. Медиана, биссектриса, высота, средняя линия
Эффективное решение существует!
После того, как вы нашли необходимые формулы и теорию для ЕГЭ по математике, рекомендуем вам перейти в раздел «Каталоги» и закрепить полученные знания на практике. Для этого достаточно выбрать задачу по данной теме и решить ее. Кроме того, справочные материалы по математике для ЕГЭ пригодятся вам и для других естественнонаучных дисциплин, таких как физика, химия и т. д.
Факт 4.
\(\bullet\) Биссектрисы смежных углов взаимно перпендикулярны.
\(\bullet\) Биссектрисы односторонних углов при параллельных прямых взаимно перпендикулярны.
Факт 5.
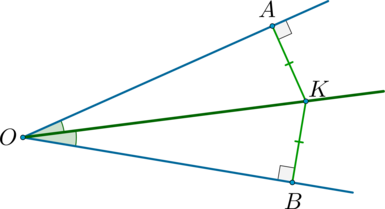
\(\bullet\) Прямая теорема: каждая точка биссектрисы угла равноудалена от сторон угла.
\(\bullet\) Обратная теорема: если точка равноудалена от сторон угла, то она лежит на его биссектрисе.
Факт 6.
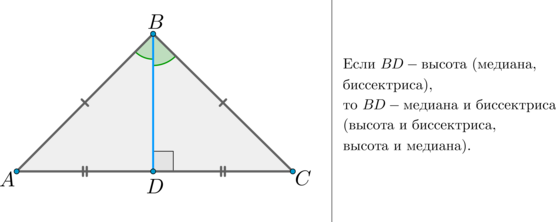
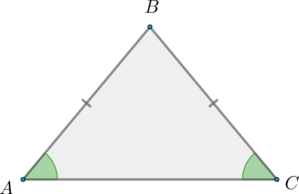
\(\bullet\) Равнобедренный треугольник – треугольник, у которого две стороны равны. Третья сторона треугольника называется основанием.
Первое свойство равнобедренного треугольника:
Второе свойство равнобедренного треугольника: углы при основании равны.
Первый признак равнобедренного треугольника: если у треугольника два угла равны, то он равнобедренный.
Второй признак равнобедренного треугольника: если у треугольника совпадают высота и медиана (высота и биссектриса или медиана и биссектриса), проведенные к одной и той же стороне, то этот треугольник является равнобедренным.
Факт 7.
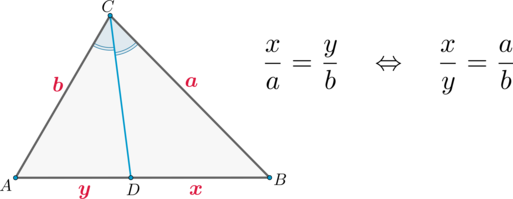
\(\bullet\) Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.
Факт 9.
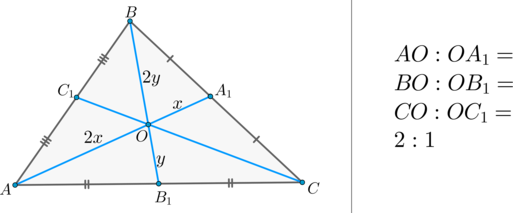
\(\bullet\) Медиана треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.
Факт 10.
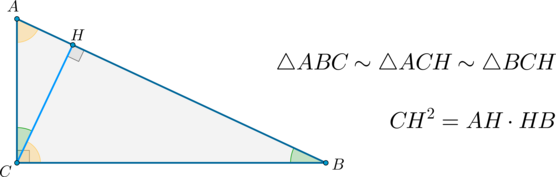
\(\bullet\) Высота, проведенная из вершины прямого угла треугольника, делит его на два треугольника, подобных исходному.
\(\bullet\) Квадрат этой высоты равен произведению отрезков, на которые она делит гипотенузу.
Факт 11.
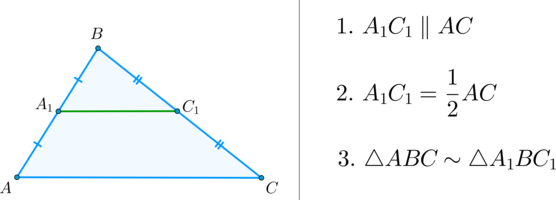
\(\bullet\) Средняя линия треугольника – отрезок, соединяющий середины двух его сторон.
\(\bullet\) 1. Средняя линия треугольника параллельна третьей стороне.
\(\bullet\) 2. Средняя линия треугольника равна половине третьей стороны.
\(\bullet\) 3. Средняя линия отсекает от треугольника подобный ему треугольник.
Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?
Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.