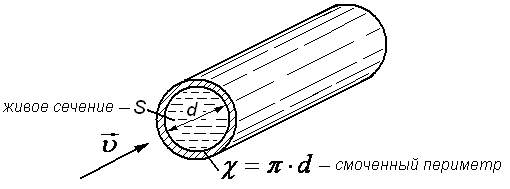Что такое смоченный периметр
Гидродинамика. Гидравлический радиус и диаметр.
Гидравлическим радиусом (R) принято обозначать соотношение площади живого сечения к смоченному периметру. Так, к примеру, для круглой трубы, работающей полным сечением, гидравлический радиус равен одной четвертой ее диаметра. Формула принимает вид:
Живым сечение (w) принято обозначать поперечное сечение потока, перпендикулярное ко всем без исключения линиям тока.
К примеру, при рассмотрении круглой трубки с диаметром d, причем все поперечное сечение заполнено жидкостью, живое сечение представлено площадью круга:
Смоченный периметр (χ) – та часть периметра живого сечения, которая граничит с твердыми стенками, формируя смоченную поверхность. К примеру, для русла вся боковая поверхность потока, без свободной плоскости, там, где жидкость граничит с газообразной средой.
Для круглой трубы, работающей полным сечением, смоченный периметр будет равняться длине окружности, значит формула примет вид:
Для круглой незаполненной трубы формула принимает вид:
Гидравлическим диаметром (D) принято обозначать соотношение учетверенной площади живого сечения к смоченному периметру:
Смоченый периметр и гидравлический радиус
Смоченный периметр потока – линия, по которой жидкость соприкасается с поверхностями русла в данном живом сечении. Длина этой линии обозначается буквой c.
В напорных потоках смоченный периметр совпадает с геометрическим периметром, так как поток жидкости соприкасается со всеми твёрдыми стенками.
Гидравлическим радиусом R потока называется часто используемая в гидравлике величина, представляющая собой отношение площади живого сечения S к смоченному периметру c:
При напорном движении в трубе круглого сечения гидравлический радиус будет равен:


т.е. четверти диаметра, или половине радиуса трубы.
Для безнапорного потока прямоугольного сечения с размерами 


Уравнение неразрывности и его физический смысл
При стационарном течении количество жидкости, втекающей в единицу времени в трубку тока через сечение 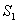



где 



Если бы это равенство не соблюдалось, то масса жидкости между сечениями 


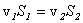 . . | (6.1) |
Это соотношение называется уравнением неразрывности. Его физический смысл заключается в том, что жидкость нигде не накапливается, то есть за одинаковый временной интервал в трубку тока втекает и вытекает равное количество жидкости. Скорость жидкости в одной и той же трубке тока больше там, где меньше площадь поперечного сечения трубки.
Уравнение Бернулли для идеальной и вязкой жидкости
Для идеальной
Поток идеальной жидкости, как указывалось ранее, можно представить совокупностью элементарных струек жидкости. Скорости по сечению потока неодинаковы, причём в середине потока скорости наибольшие, а к периферии они уменьшаются (струйная модель потока). Это означает, что различные струйки в одном сечении имеют различные значения кинетической энергии. Отсюда следует, что кинетическая энергия, посчитанная с использованием скоростей элементарных струек uS, и кинетическая энергия, посчитанная с использованием значения средней скорости потока V, будет иметь разные значения. Выясним, какова эта разница. Кинетическая энергия элементарной струйки 
где 




Проинтегрировав выражение для 

Для вязкой
Перед тем, как записать уравнение Бернулли для потока вязкой жидкости необходимо оговорить два момента. Поток жидкости отличается от элементарной струйки тем, что он имеет реальные размеры поперечного сечения, которые могут быть довольно значительных размеров. Распределение давлений и скоростей по сечению потока может быть неравномерным.
Рассмотрим распределение давления. В плоскости перпендикулярной направлению движения, гидродинамическое давление распределяется по закону гидростатики. В связи с этим справедливо условие:
т.е. сумма отметки z и пьезометрической высоты 
В связи с тем, что распределение местных скоростей U в плоскости сечения потока неравномерно и в большинстве случаев неизвестно, то возникают трудности с определением кинетической энергии потока, т.е. с третьим слагаемым в уравнении Бернулли 
Для наиболее распространенных случаев движения жидкости значения ± следующее: при ламинарном движении в круглой трубе ± = 2, при турбулентном – зависит от режима и принимает значение ± = 1,1 
Коэффициент Кориолиса
Коэффициент Кориолиса представляет собой отношение действительной кинетической энергии к кинетической энергии потока, вычисленной по средней скорости. Таким образом, поправочный коэффициент учитывает неравномерность скорости по живому сечению потока.
Коэффициент Кориолиса зависит от режима течения жидкости.
Для ламинарного режима = 2.
Для турбулентного режима = 1,13…1,15
Что такое смоченный периметр
Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют. Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.
если угол в радианах, или
Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.
Течение жидкости может быть установившимся и неустановившимся. Установившимся движением называется такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени
Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным
Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.
Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений. Представим трубу с переменным живым сечением (рис.3.4). Расход жидкости через трубу в любом ее сечении постоянен, т.е. Q1=Q2= const, откуда
Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:
Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого уравнения решается большой круг задач.
Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис.3.5).
Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.
Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.
Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис.3.5).
Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.
Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.
Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:
Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:
и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.
С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:
Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.
В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.
Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения
Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3.6).
Потерянная энергия или потерянный напор обозначаются 
Уравнение Бернулли для реальной жидкости будет иметь вид:
Из рис.3.6 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.
Кроме этого в уравнении появились еще два коэффициента α1 и α2, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ).
Потерянная высота 
Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис.3.7), загнутый конец которой направлен навстречу потоку. Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим
Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.
Выражение, стоящее перед 
Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.
Гидравлический радиус



В гидравлических расчётах для характеристики размеров и формы поперечного сечения потока вводят понятие о живом сечении и его элементах: смоченном периметре и гидравлическом радиусе.
Живым сечением называется поверхность в пределах потока, проведённая нормально к линиям тока.
Для круглого трубопровода, когда всё поперечное сечение заполнено жидкостью, живым сечение является площадь круга: 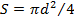
Рис. 3.6. Элементы потока
Смоченным периметром называют ту часть периметра живого сечения, по которой жидкость соприкасается со стенками трубопровода (рис.3.6). Смоченный периметр обычно обозначают греческой 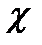
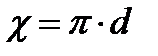
Гидравлическим радиусом называют отношение живого сечения к смоченному периметру, т.е. величину
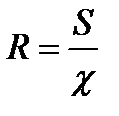
Эта величина характеризует удельную, т.е. приходящуюся на единицу длины смоченного периметра, площадь живого сечения. Легко сделать вывод, что поток с наибольшим гидравлическим радиусом при прочих равных условиях имеет минимальную силу трения, приложенную к смоченной поверхности.
Для круглых труб, полностью заполненных жидкостью, гидравлический радиус равен четверти диаметра:
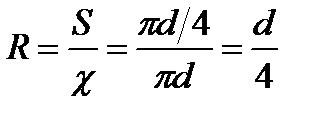
Введение гидравлического радиуса как характерного размера позволяет сравнивать по критерию подобия (Re) потоки с разными формами живого сечения.
Рассмотренные основные понятия позволяют решать самые различные практические задачи гидравлики.
Решение. Искомая скорость 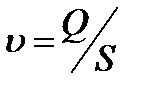
Определим площадь живого сечения:
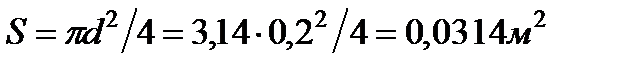
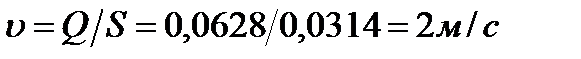
Будь умным!
Работа добавлена на сайт samzan.ru: 2015-07-05
«>32. Гидравлические характеристики поперечного сечения потока.
Смоченный периметр χ это периметр той части поперечного сечения русла, которая смочена движущейся жидкостью, или периметр твердых границ потока (рис. 5.2).
Связь между указанными расходами установим в виде
Весьма важной характеристикой живого сечения является средняя скорость V, которая определяется зависимостью
В последующем изложении потребуется рассматривать не только поток объема, веса или массы жидкости через живое сечение, но также и поток кинетической энергии жидкости и поток количества движения жидкости через живое сечение. Выразим эти величины через среднюю скорость жидкости V в поперечном сечении.
Поток кинетической энергии Q к через живое сечение га, согласно (3.13) и (3.10), равен
Множитель α называется коррективом кинетической энергии, или коэффициентом Кориолиса. Согласно (5.11),
Как показывают расчеты, в большинстве встречающихся на практике потоков α = 1,05. 1,10.
Поток количества движения Q I через живое сечение ω в соответствии с (3.13) и (3.11) равен
т.е. корректив количества движения представляет собой отношение потока количества движения через живое сечение, вычисленного при реальном распределении скорости по живому сечению, к потоку количества движения, вычисленному в предположении, что скорость жидкости в живом сечении постоянна и равна средней скорости. При решении технических и технологических задач для большинства потоков принимают α 0 = 1,03. 1,07.
«>33. Уравнение неразрывности.
«>Рассмотрим установившееся движение жидкости при отсутствии фазовых переходов в трубе с произвольно изменяющимся по ее длине поперечным сечением (рис. 5.3). Пусть в этой трубе есть сечения, где движение равномерное или близкое к нему, т.е. плавноизменяющееся, например, сечения 1 1, 33, 22.
«>Зафиксируем в качестве контрольного объем V трубопровода между сечениями 11 и 22, контрольная поверхность А показана на рис. 5.3 штриховой линией. Запишем для этого контрольного объема закон сохранения массы:
«>Используя представление субстанциальной производной в виде суммы локальной и конвективной составляющих, перепишем (5.16) в виде
«>При установившемся движении плотность ρ, как и размеры и очертание контрольного объема V, не зависит от времени. Поэтому первое слагаемое в левой части уравнения (5.17) равно нулю. В результате(5.18)
«>где А = ω ;vertical-align:sub»> 1 «>+ω ;vertical-align:sub»>2 «>+ » xml:lang=»en-US» lang=»en-US»>A ;vertical-align:sub»>бок «>, » xml:lang=»en-US» lang=»en-US»>ω ;vertical-align:sub»>1 «>, » xml:lang=»en-US» lang=»en-US»>ω ;vertical-align:sub»>2 «>площади живых сечений 1 1 и 22, А ;vertical-align:sub»>бок «> площадь боковой поверхности трубы. Очевидно, что на боковой поверхности » xml:lang=»en-US» lang=»en-US»>u ;vertical-align:sub» xml:lang=»en-US» lang=»en-US»>n «> = 0, следовательно,
«>Как было определено выше, масса жидкости, протекающей в единицу времени через некоторую поверхность, называется массовым расходом. Следовательно, вместо (5.20) можно записать » xml:lang=»en-US» lang=»en-US»>Q ;vertical-align:sub» xml:lang=»en-US» lang=»en-US»>M ;vertical-align:sub»>1 «> = (5.21)
«>где » xml:lang=»en-US» lang=»en-US»>Q ;vertical-align:sub» xml:lang=»en-US» lang=»en-US»>M ;vertical-align:sub»>1 «> и » xml:lang=»en-US» lang=»en-US»>Q ;vertical-align:sub» xml:lang=»en-US» lang=»en-US»>M ;vertical-align:sub»>2 «> массовые расходы в сечениях 1 1 и 22, соответственно. Проведя аналогичные рассуждения относительно любого другого сечения, например, 33, получим » xml:lang=»en-US» lang=»en-US»>Q ;vertical-align:sub» xml:lang=»en-US» lang=»en-US»>M ;vertical-align:sub»>1 «>= » xml:lang=»en-US» lang=»en-US»>Q ;vertical-align:sub» xml:lang=»en-US» lang=»en-US»>M ;vertical-align:sub»>2 «>= » xml:lang=»en-US» lang=»en-US»>Q ;vertical-align:sub» xml:lang=»en-US» lang=»en-US»>M ;vertical-align:sub»>3 «> (5.22) т.е. при движении жидкости в трубе с непроницаемыми стенками массовый расход вдоль потока остается постоянным: » xml:lang=»en-US» lang=»en-US»>Q ;vertical-align:sub» xml:lang=»en-US» lang=»en-US»>M «> = соп » xml:lang=»en-US» lang=»en-US»>st «> (вдоль потока). (5.23)
«>Для несжимаемой жидкости при р = с » xml:lang=»en-US» lang=»en-US»>onst «> равенство (5.21) записывается для объемного расхода » xml:lang=»en-US» lang=»en-US»>Q «> в виде » xml:lang=»en-US» lang=»en-US»>Q ;vertical-align:sub»>1 «> = = » xml:lang=»en-US» lang=»en-US»>Q ;vertical-align:sub»>2 «> (5.24)
«>или О = со » xml:lang=»en-US» lang=»en-US»>nst «> (вдоль потока). (5.25). Полученные равенства (5.21)(5.25) называются уравнениями «> неразрывности. «>Используя понятие средней скорости и полагая, что в живом сечении плотность жидкости постоянна, запишем уравнение неразрывности (5.21) в виде ρ ;vertical-align:sub»>1 » xml:lang=»en-US» lang=»en-US»>v ;vertical-align:sub»>1 «>ω ;vertical-align:sub»>1 «>= ρ ;vertical-align:sub»>2 » xml:lang=»en-US» lang=»en-US»>v ;vertical-align:sub»>2 «>ω ;vertical-align:sub»>2 «>(5.26) или для несжимаемой жидкости » xml:lang=»en-US» lang=»en-US»>v ;vertical-align:sub»>1 «>ω ;vertical-align:sub»>1 «>= » xml:lang=»en-US» lang=»en-US»>v ;vertical-align:sub»>2 «>ω ;vertical-align:sub»>2 «>(5.27)
«>Последнее равенство называют уравнением неразрывности в форме Леонардо да Винчи.
«>Если все характеристики потока не зависят от какой-либо одной координаты, например от у, можно рассматривать изменение их только в плоскости (х, г), т.е. решать так называемую «> плоскую задачу. «>В указанном случае можно перейти к удельным характеристикам, приходящимся на единицу линейного размера потока в направлении оси у. Так, например, равномерное безнапорное течение в прямоугольном канале (рис. 5.4), ширина » xml:lang=»en-US» lang=»en-US»>b «> «>которого намного больше глубины потока » xml:lang=»en-US» lang=»en-US»>h «>, «> можно рассматривать как плоское. «> Удельным расходом «> называют объемный расход, приходящийся на единицу ширины потока:
» xml:lang=»en-US» lang=»en-US»>q «>= (5.28). Поскольку продольная скорость » xml:lang=»en-US» lang=»en-US»>u ;vertical-align:sub»>х «>зависит только от координаты » xml:lang=»en-US» lang=»en-US»>z «>, «> ее распределение по вертикали обычно изображают в виде «> эпюры скорости «>u ;vertical-align:sub»>x «> = » xml:lang=»en-US» lang=»en-US»>u ;vertical-align:sub» xml:lang=»en-US» lang=»en-US»>x «>( » xml:lang=»en-US» lang=»en-US»>z «>), а элементарную площадь поперечного сечения » xml:lang=»en-US» lang=»en-US»>d «>А представляют в виде » xml:lang=»en-US» lang=»en-US»>d «>А = » xml:lang=»en-US» lang=»en-US»>bdz «>. В соответствии с (5.8) средняя скорость (5.29) Согласно (5.29), в условиях плоской задачи средняя скорость численно равна высоте прямоугольника, равновеликого эпюре скорости.
«>34.Уравнение Бернулли для установившегося напорного потока вязкой несжимаемой жидкости.
Уравнение Бернулли, относится к установившимся напорным потокам вязкой жидкости. В некоторых случаях возникает необходимость в более общей форме этого уравнения, относящейся к неустановившимся напорным потокам несжимаемой (р = const ) жидкости в трубах с абсолютно жесткими (недеформируемыми) стенками в фиксированный момент времени.
Для неустановившегося движения в выражении для субстанциальной производной (5.38) нельзя полагать равной нулю локальную составляющую, так как скорость жидкости зависит от времени:
Это слагаемое без преобразований войдет в окончательную форму уравнения Бернулли (5.47), которое для неустановившегося движения примет вид
(5.60). Величина h ин представляет собой изменение в единицу времени кинетической энергии жидкости в контрольном объеме V (при неустановившемся движении), отнесенное к весовому расходу, и называется инерционным напором.Уравнение (5.59) справедливо для каждого фиксированного момента времени t = t ф из временного интервала, в течение которого рассматривается неустановившееся движение. При этом следует иметь в виду, что инерционный напор представляет собой не потерянную (диссипированную) механическую энергию, а изменение механической энергии потока между сечениями 1 1 и 22, обусловленное локальным изменением кинетической энергии в каждой точке потока. Инерционный напор может быть как положительным, если кинетическая энергия жидкости в контрольном объеме увеличивается во времени, так и отрицательным в противном случае. Следовательно, эта величина является дополнением к изменению энергии, обусловленному переносом (конвекцией) кинетической энергии через живые сечения. Учитывая это, иногда целесообразно включать инерционный напор в полный напор во втором сечении:
При этом уравнение Бернулли для установившегося и неустановившегося движений имеет одинаковую форму (5.54).
Организуем эксперименты следующим образом. Зафиксируем значения рил (т.е. используем в качестве рабочей жидкости, например, воздух при заданных температуре и давлении). Поместим цилиндр диаметром D и шероховатостью А в поток жидкости (например, в аэродинамическую трубу) и, задавая несколько значений скорости воздуха V „,, с помощью динамометра определим силу, действующую на единицу длины цилиндра. В результате получим зависимость F = f 1 ( V ∞ ). Изменив шероховатость поверхности цилиндра (наклеив на его поверхность другие песчинки) и проведя такие же опыты, получим F = f 2 ( V ∞ ). Использовав песчинки десяти различных размеров (чтобы изучить возможно более широкий диапазон встречающихся на практике шероховатостей), представим результаты экспериментов в виде графика (рис. 24.1).
Основные положения анализа размерностей. П-теорема
Основой анализа размерности является положение о том, что все математические равенства, выражающие связь между физическими величинами (параметрами потока жидкости или газа в гидромеханике), должны быть размерно-однородными или однородными по размерностям. Это означает, что:
размерность правой части равенства должна быть такой же, как и размерность левой части того же равенства;
складывать и вычитать можно только величины, имеющие одинаковые размерности.
Эти очевидные правила (вряд ли кому-нибудь представится возможность сложить один килограмм с один метром) позволяют получить нетривиальные результаты, что вызывает у начинающих исследователей настороженное отношение к анализу размерностей. С одной стороны, результаты получаются как бы «из ничего», из бесспорных предпосылок, которые не похожи на привычный фундамент физических наук; с другой стороны, результаты не имеют вида окончательных физических зависимостей, они требуют дополнительного, чаще всего экспериментального изучения явлений.
Продемонстрируем на примерах основные особенности технических приемов, используемых в анализе размерностей, и возможности, которые он предоставляет.
Предварительно зафиксируем, что в механике жидкости и газа используются первичные размерности: масса М; длина L ; время Т; температура 0.
В качестве примера, на котором могут быть показаны основные приемы анализа размерности, рассмотрим задачу с распространением возмущения свободной поверхности в покоящейся жидкости, заполняющей широкий прямоугольный канал с горизонтальным дном (рис. 24.2). Жидкость имеет плотность ρ, она невязкая (η = 0), влиянием боковых стенок пренебрегаем и изменение всех характеристик рассматриваем лишь в плос-
Покажем, как аналогичный результат можно получить, используя анализ размерностей. Здесь следует выделить несколько этапов решения задачи.
Все величины, от которых зависит значение с, имеют различные размерности. Поскольку в соответствии с положением об однородности по размерностям их нельзя суммировать, то остается только возможность добиться одинаковой размерности левой и правой частей (24.2), возводя эти величины (ρ, h 0 и g ) в какие-либо степени и составляя произведения из этих степеней:
2-й этап. Подставим вместо всех величин, входящих в (24.4), размерности и потребуем, чтобы размерность левой части была равна размерности правой:
Приравняв показатели степени у одноименных размерностей, получим систему уравнений:
Решив эту систему, найдем
В результате выражение (24.2) приобретает вид
Кроме того, анализ размерностей позволил установить, что скорость с не зависит от рода жидкости, т.е. и в воде и в ртути скорость распространения возмущений свободной поверхности одинакова.
Отметим, что приведенный пример показал основные особенности анализа размерностей. С одной стороны, не проводя экспериментов и не используя физических законов, только из условий однородности по размерности мы установили, что скорость с не зависит от рода жидкости, установили структуру зависимости с от глубины. С другой стороны, полученная зависимость (24.5) дает лишь структуру зависимости и требует дополнительных (но, что существенно, значительно меньших по объему) исследований (экспериментальных или теоретических).
Рассмотрим ту же задачу о скорости распространения возмущения в канале.
Как и в предыдущей задаче, представим зависимость (24.6) в виде (24.7)
2-й этап. Подставив в (24.7) размерности (24.8)
и приравняв показатели степени у М, L и Т, получим (24.9)
3-й этап. Полученная система уравнений не имеет единственного решения, так как здесь количество неизвестных (4) больше количества уравнений (3). Одну из неизвестных X ; можно задать. Пусть это будет х 4 ; выразив остальные неизвестные через нее:
Поскольку x 4 является произвольным безразмерным числом, то полученный результат можно интерпретировать следующим образом. Положим, что х 4 = 1, 2, 3. ; при этом с можно представить в виде ряда (24.11)
Этот ряд (если он сходится, что вполне правдоподобно при h B h 0 ) представляет собой некоторую неизвестную функцию Тогда зависимость (24.11) можно записать в виде ( 24.12)
определению с как функции одной переменной h B / h 0
В общем виде полученный частный результат формулируется в виде так называемой Н-теоремы, которую приведем без доказательства.
Если физический процесс описывается однородным по размерности равенством
Название П-теоремы происходит от использованной для обозначения безразмерных параметров греческой буквы П. Эту теорему часто связывают с именем Бэкингэма, хотя анализ размерности впервые был предложен Фурье.
В разделе 24.1 было показано, что в конечном итоге все задачи экспериментального исследования гидромеханических явлений связаны с вопросами их подобия и моделирования, поэтому для установления набора безразмерных параметров, позволяющих эффективно решать ту или иную задачу, обратимся к общим вопросам о подобии и моделировании физических процессов.
«>51.Подобие гидромеханических явлений. Геометрическое, кинематическое и динамическое подобие потоков жидкости и газа.
«>Для того, чтобы два гидромеханических объекта (два потока жидкости или газа) были подобны, необходимо соблюдение трех типов подобия этих явлений (потоков):
«>геометрическое «>подобие; «>кинематическое «>подобие; «>динамическое «>подобие.
«>Для определенности будем считать один из объектов натурным, или прототипом, а второй объект модельным; все параметры натурного объекта обозначим индексом «н», а модельного «м».
«>Геометрическое «>подобие натурного и модельного объектов обеспечивается, если подобны все треугольники, связывающие сходственные точки физических границ этих объектов.
«>Так, на рис. 24.3 подобны треугольники А ;vertical-align:sub»>М «>В ;vertical-align:sub»>М «>Е ;vertical-align:sub»>М «> и А ;vertical-align:sub»>Н «>В ;vertical-align:sub»>Н «>Е ;vertical-align:sub»>Н «>; » xml:lang=»en-US» lang=»en-US»>C ;vertical-align:sub» xml:lang=»en-US» lang=»en-US»>M » xml:lang=»en-US» lang=»en-US»>B ;vertical-align:sub» xml:lang=»en-US» lang=»en-US»>M » xml:lang=»en-US» lang=»en-US»>D ;vertical-align:sub» xml:lang=»en-US» lang=»en-US»>M «> и » xml:lang=»en-US» lang=»en-US»>C ;vertical-align:sub» xml:lang=»en-US» lang=»en-US»>H » xml:lang=»en-US» lang=»en-US»>B ;vertical-align:sub» xml:lang=»en-US» lang=»en-US»>H » xml:lang=»en-US» lang=»en-US»>D ;vertical-align:sub» xml:lang=»en-US» lang=»en-US»>H «> и т.д. Постоянное отношение расстояния между двумя произвольными точками модельного объекта к расстоянию между соответствующими точками натурного объекта называется «>линейным масштабом модели: «>
«>Из определения геометрического подобия следует, что угол между двумя плоскими элементами физических границ в модельном объекте равен углу между соответствующими элементами натурного объекта.
«>Геометрическое подобие криволинейных границ потока обеспечивается аппроксимацией с необходимой точностью этих границ кусочно-плоскими поверхностями. При этом, в частности, круглоцилиндричес-кой поверхности диаметром » xml:lang=»en-US» lang=»en-US»>D ;vertical-align:sub» xml:lang=»en-US» lang=»en-US»>H «> в натурном объекте будет соответствовать в модельном объекте также круглоцилиндрическая поверхность диаметром » xml:lang=»en-US» lang=»en-US»>D ;vertical-align:sub» xml:lang=»en-US» lang=»en-US»>M «>= » xml:lang=»en-US» lang=»en-US»>M «> ;vertical-align:sub» xml:lang=»en-US» lang=»en-US»>l «> » xml:lang=»en-US» lang=»en-US»>D ;vertical-align:sub» xml:lang=»en-US» lang=»en-US»>H «>.
«>Кинематическое «>подобие предполагает, что картина течения в модельном объекте подобна натурной картине течения, другими словами, в сходственных точках скорости жидкости (или какая-либо другая скорость, например, скорость движущегося в жидкости тела) в натурном и модельном объектах одинаково ориентированы относительно физических границ, а отношение значений модельной и натурной скоростей, которое называется масштабом скорости, постоянно во всех точках потока: (24.16)
«>Это условие особенно важно при возможности образования отрывных течений: одни и те же физические границы могут формировать качественно различающиеся картины течения; примеры таких течений, когда физическими границами являются труба с резким увеличением диаметра и круговой цилиндр, представлены на рис. 24.4 и 24.5, соответственно. Очевидно, что потоки при безотрывном обтекании физических границ (рис. 24.4,а и 24.5, » xml:lang=»en-US» lang=»en-US»>a «>) не подобны кинематически потокам, имеющим отрывные зоны (водовороты, каверны и т.п. на рис. 24.4,6’и 24.5,6), и следовательно, такие пары течений не могут рассматриваться как модельный и натурный объекты.
«>Динамическое «>подобие потоков формулируется на основе закона подобия Ньютона, согласно которому в каждой из сходственных точек модельного и натурного потоков «>многоугольники сил, «>действующих на каждую жидкую частицу (включая силу инерции), должны быть: «>подобны, «>причем коэффициент подобия (масштаб сил должен быть постоянен во всей области течения; «>одинаково ориентированы «>относительно физических границ (рис. 24.6).
«>52. Критерии динамического подобия, их роль и физический смысл.
Такие равенства, записанные для различных сочетаний сил, формирующих течение жидкости, рассматривают как «> критерии динамического подобия натурного и модельного объектов.
«>Рис. 24.6. Динамическое подобие гидравлических объектов: а модельный объект; б натурный объект
В большинстве задач гидромеханики сила инерции жидкой частицы является формирующей течение силой, в то время как силы другой природы (силы вязкости, давления, тяжести, электромагнитного происхождения, поверхностного натяжения) не всегда вносят ощутимый вклад в баланс сил, и в отдельных задачах те или иные силы целесообразно исключать из рассмотрения, считая их вклад исчезающе малым. С учетом этого принято при составлении критериев подобия рассматривать отношения внешних для заданной жидкой частицы сил к силе инерции этой частицы.
Оценим значения сил, действующих на жидкие частицы, полагая на основании изложенного выше, что характерная для данного объекта площадь поверхности, на которую действует сила, равна » xml:lang=»ru-RU» lang=»ru-RU»>ℓ ;vertical-align:super» xml:lang=»ru-RU» lang=»ru-RU»>2 » xml:lang=»ru-RU» lang=»ru-RU»>, характерный
Э и и объем » xml:lang=»ru-RU» lang=»ru-RU»>ℓ ;vertical-align:super» xml:lang=»ru-RU» lang=»ru-RU»>3 » xml:lang=»ru-RU» lang=»ru-RU»>, а пространственная производная скорости ∂ u /∂ℓ
Сила инерции F ин жидкой частицы равна произведению ее массы ρℓ 3 на ускорение; при установившемся
движении ускорение жидкой частицы (24.18)
Аналогично найдем выражение для других сил:
Сила вязкости: (24.20)
Сила давления (24.21)
Составим отношение значений каждой из трех последних сил к силе инерции (24.18) для модельного объекта и приравняем соответствующим отношением для натурального объекта.
Безразмерное выражение называют числом Фр y да и обозначают:
Число Фруда является критерием динамического подобия, если в состав сил, определяющих гидродинамическое явление входят силы тяжести и инерции. Используя (24.23), условие подобия (24.22) представим в виде
Безразмерное выражение uℓ/ν называют числом Рейнольдса и обозначают
Число Рейнольдса является критерием динамического подобия, если в состав сил, формирующих поток, входят силы вязкости и инерции. Используя (24.25) в виде
Безразмерное выражение называют числом Эйлера или коэффициентом давления и обозначают Еu (множитель ½ вводят в знаменательно, чтобы последний был близок к скоростному напору в уравнении Бернулли):
«>Число Эйлера обычно не рассматривается как независимый критерий динамического подобия; согласно уравнениям гидродинамики (в частности, уравнению Бернулли), поле давления и поле скорости жидкости связаны друг с другом; перепад давления Δрнапример, при обтекании жидкостью твердого тела связан со скоростью потока, а скорость потока связана с перепадом давления, так что значение числа Эйлера, как правило, не может рассматриваться как независимый критерий подобия. Вместе с тем, в динамически подобных потоках
( «>Еu) ;vertical-align:sub»>м «>= ( «>Еu) ;vertical-align:sub»>н «>(24.29)
Кроме критериев подобия, получаемых из закона динамического подобия Ньютона, при моделировании гидромеханических явлений необходимо принимать во внимание еще целый ряд безразмерных величин.
;font-family:’Times New Roman'» xml:lang=»ru-RU» lang=»ru-RU»>ИЛИ
4. При моделировании натурных объектов, в которых возможны эффекты, связанные со «> сжимаемостью жидкости, в качестве критерия подобия следует использовать «> число Маха
где а скорость звука в жидкости.
При этом для подобия модельного и натурного объектов необходимо равенство М м =М н (24.31)
Кроме того, в этом случае следует включить в число независимых безразмерных параметров, определяющих подобие процессов, и показатель адиабаты k = c p / c V
5. При необходимости учесть «> поверхностные эффекты на границе, разделяющей различные жидкости (например, воду и воздух), в число критериев подобия включают «> число » xml:lang=»be-BY» lang=»be-BY»>В «>ебера
Где σ коэффициент поверхностного натяжения.
Этот критерий следует учитывать, рассматривая лишь течения тонких слоев жидкости со свободной поверхностью (пленочные течения).
6. При «> нестационарных граничных условиях, когда, например, какое- нибудь твердое тело колеблется с некоторой частотой Ωв потоке жидкости, из трех размерных величин, определяющих этот процесс: из скорости потока и, линейного размера тела ℓи частоты Ω можно образовать безразмерную величину, которую называют «> числом Струхала:
Если колебания тела задаются внешней по отношению к потоку силой (рис. 24.7), то число Струхала является «> независимым критерием подобия, и при изучении этого явления на модели следует потребовать выполнения условия:
В некоторых случаях колебания тела в турбулентном потоке обуслов- лены именно обтеканием его жидкостью, образованием за телом турбу-лентного следа, цепочки вихрей и т.п. Такие явления приходится рас- сматривать при проектировании дымовых труб, мостов, линий электро-
передач; здесь число Струхала это зависимый безразмерный параметр, а независимыми будут число Рейнольдса и, возможно,число Маха.
Безразмерные параметры, представляющие собой произведения величин, имеющиотличающиеся друг отдруга размерности (например, числа Рейнольдса, Фруда и т.п.), называют безразмерными «> комплексами. Наряду с ними, используют безразмерные параметры в виде отношения двух величин, имеющих одинаковую размерность; например, число Маха, относительная ширина открытого потока β=b/h, относительная шероховатость Δ г = Δ/ ℓ (в круглой трубе ℓ диаметр D, а в открытом русле ℓ глубина потока h), относительная длина трубы ℓ/ D и т.п. Такие параметры называются безразмерными «> симплексами.
Безразмерные комплексы и симплексы, которые используются как «>критерии подобия (для обеспечения геометрического и динамического подобия), называют «> независимыми безразмерными параметрами подобия. Кроме них в гидромеханике используют так называемые «> зависимые (искомые) «>безразмерные параметры подобия. В их число входят из приведенных выше число Эйлера Еu, в некоторых задачах число СтрухалаSh. Кроме этих чисел, зависимыми безразмерными параметрами являются:
коэффициент местной потери напора: (24.37)
коэффициент лобового сопротивления движущегося тела: (24.38)
Зависимые (искомые) безразмерные параметры рассматривают как функцию от независимых (задаваемых) безразмерных параметров.
Материалы собраны группой SamZan и находятся в свободном доступе