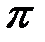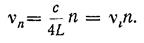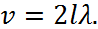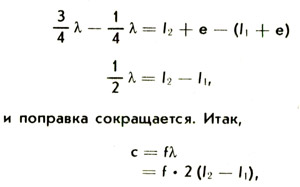Что такое собственная частота столба воздуха в трубе

Определение скорости звука в воздухе и собственных частот воздушного столба

Краткая теория.Звуковые волны характеризуются частотой v, длиной волны λ и скоростью распространения с. Между собой они связаны соотношением

Для определения скорости звука в большинстве случаев изме­ряют частоту звука и соответствующую длину волны. Для измерения длины волны можно воспользоваться явлением акустического резонан­са. Пусть имеется труба, закрытая с одного конца. Если к отверстию трубы поднести источник звука, то в столбе воздуха, находящегося в трубе, возникнут колебания с частотой, создаваемой источником звука. Явление резонанса будет наблюдаться всякий раз, когда час­тота вынужденных колебаний будет практически совпадать с соб­ственной частотой воздушного столба. Собственные же частоты ко­лебаний воздушного столба определяются его длиной и скоростью распространения звука в воздухе. Теоретические расчеты показывают, что собственные частоты воздушного столба могут быть вычис­лены по следующей формуле:

(1 )

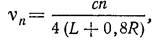
где п = 1, 3, 5. ; L — длина воздушного столба; R — радиус воз­душного столба, т. е. радиус трубы, в которой находится столб воз­духа. Если радиус воздушного столба по сравнению с его длиной мал, т. е. R

Задание. 1. Задайте определенную частоту звуковых колебаний в интервале 300—500 гц, измерьте длину волны и вычислите скорость распространения звука в воздухе.

,

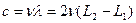
где L₂, L₁ расстояния уровня воды при двух последующих резонансах звука в воздушном столбе.

Измерения повторите не менее чем для трех различных частот.

2. Найдите собственные частоты колебаний воздушного столба заданной длины, изменяя для этого частоту, задаваемую генератором. Сверьте полученные данные с рассчитанными по формуле

3. Найдите погрешности измерения скорости звука в воздухе и укажите возможные их причины.

Источник

;

, где k=0,1,2,…

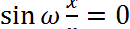
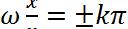
Следовательно, координаты узлов:.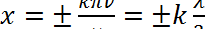

Расстояние между соседними узлами :.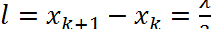

Обычно стоячие волны возникают при распространении упругих колебаний в телах ограниченных размеров. Вследствие многократных отражений от границ тела с окружающей средой падающая волна вызывает множество отраженных волн. Если размеры тела таковы, что отраженные волны, взаимодействуя, усиливают друг друга, то амплитуда результирующего колебания возрастает – наступает резонанс.

Таким образом, наименьшая разность длин воздушных столбов, в которых возникает резонанс, равна ,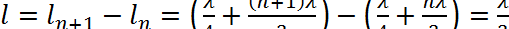

Откуда 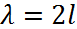, а скорость волны

Вопросы для самоконтроля

1. Звуковые волны в различных средах.

2. Выведите уравнение бегущей волны.

3. Объясните возникновение стоячей волны.

4. Почему стоячая волна не переносит энергии?

5. Как изменяется фаза звуковой волны при отражении от границы раздела воздух-вода?

6. Объясните возникновение резонанса звуковых колебаний в трубе с воздухом.

Определение скорости звука в воздухе

ЦЕЛЬ РАБОТЫ: овладеть методикой определения скорости звука в воздухе методом стоячих волн – методом Кундта.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: установка для определения скорости звука в воздухе методом стоячих волн (методом резонанса).

Установка для образования стоячих звуковых волн (рис.2) состоит из звукового генератора (1), телефона 2 и стеклянной трубки 3, в которую налита вода. Уровень воды в трубке можно изменять, поднимая или опуская сосуд 4, соединенный с трубкой резиновым шлангом 5.Телефон размещен у открытого конца трубки. Трубка снабжена шкалой 6, которая дает возможность определять высоту столба жидкости.

Источником звука является телефон, на который от генератора подаются электрические сигналы звуковой частоты. Телефон возбуждает колебания столба воздуха в стеклянной трубке, звуковые волны, дойдя до поверхности воды в трубке, отражаются от нее и идут в обратном направлении. Так как отражение происходит от среды акустически более плотной, наблюдается антифазное отражение, т.е. на границе раздела сред фаза отраженной волны скачком изменяется на π.

При определенных длинах воздушных столбов в трубке возникает акустический резонанс, который можно легко обнаружить по максимально звучанию воздушного столба. Наступление резонанса означает, что в трубке образовалась стоячая волна.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Переведя регулятор напряжения выхода 4 (рисунок 5) звукового генератора ГЗ-63 в крайнее левое положение, минимальное напряжение тумблером I включить генератор.

2. К выходу генератора 9 и: 9а подключить телефон (рисунок 2). Ручкой «установка частоты» 3 по индикатору «частота 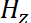» 2 установить частоту в диапазоне 1000-2000 Гц.

3. Добиться оптимальной громкости звука с помощью регулятора.

4. Осторожно перемещается сосуд 4 (рисунок 2) вверх, предварительно ослабив винт 8, поднять уровень воды в трубе 3 на максимальную высоту. (Уровень воды не должен быть ближе 5-7 см от края трубы I).

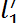
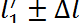
5. Медленно понижая уровень воды, грубо находим положение границы раздела, при котором имеет место максимальное усиление звука (резонанс). Затем подходим к резонансу сверху (опуская уровень воды) и снизу (поднимая уровень воды). Полученные значения уровней по линейке 6 (рисунок 2), заносим в таблицу. Эту операцию проводим не менее трех раз. Обработав полученные значения найдем величину .

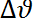
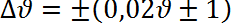
6. Записываем в таблицу значение температуры среды и частоту генератора. Ошибка определения частоты дается формулой:

.

7. Найти положение второго и третьего резонансов, как указано в пункте 5.

8. Операции 5-7 проделать не менее чем для четырех значений частот в диапазоне 1000-2000 Гц.

9. По формулам (13) и (14) рассчитать скорость звука для каждой из частот. 10. Оценить ошибку определения скорости звука .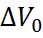

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Что такое собственная частота столба воздуха в трубе

В узкой неограниченной трубе, как и в неограниченной среде, могут существовать свободные гармонические волны любой частоты, как бегущие, так и стоячие. Иначе обстоит дело с волнами в конечном отрезке трубы, закрытом крышками, через которые звук не проходит. В таком отрезке трубы возможны только стоячие волны, и притом только определенных дискретных частот. Эти стоячие волны называют собственными колебаниями трубы. Основная задача о звуке в отрезке трубы заключается в нахождении этих дискретных частот собственных колебаний.

Начнем с простейшего случая труб, закрытых абсолютно жесткими или абсолютно мягкими крышками. Конечно, осуществление таких крышек возможно только с некоторой степенью точности: практически крышка может быть только достаточно жесткой или достаточно мягкой, в том смысле, что дальнейшее увеличение степени жесткости или податливости крышки уже не меняет заметно искомые частоты стоячих волн. Для труб, заполненных газом, осуществление достаточно жестких крышек труда не представляет. Для жидкости крышка из твердого материала будет достаточно жесткой только при достаточной ее толщине; заметим, что при заполнении трубы жидкостью возникает также и вопрос о достаточной степени жесткости боковых стенок (см. ниже, § 68).

Абсолютно мягкой «крышкой» явится, конечно, граница, с вакуумом. Но такая граница неосуществима для газов. Почти абсолютно мягкая «крышка» узкой трубы осуществляется гораздо проще — открыванием конца трубы: практически давление (звуковое, а не атмосферное!) у открытого конца трубы равно нулю (расталкивать частицы среды в стороны в неограниченной среде легче, чем продвигать в одном направлении столб среды длиной порядка длины волны). Все же давление у открытого конца не в точности равно нулю. Мы еще вернемся к этому вопросу при расчете излучения звука открытым концом трубы.

Итак, обратимся к расчету частот гармонических колебаний, возможных в ограниченной трубе. Начнем со случая идеальных крышек. На абсолютно жестких крышках скорости частиц обращаются в нуль. Поэтому на крышках должны оказаться пучности давления, и, следовательно, на длине трубы уложится целое число полуволн. Отсюда следует, что для волновых чисел при

собственных колебаниях должно удовлетворяться уравнение

где длина трубы и Каждому значению I соответствует значение волнового числа стоячей волны, возможной в данной трубе; никаких других гармонических волн в трубе быть не может. Этот набор волн образует полную систему гармонических волн в трубе с жесткими крышками. Давление в волне номера распределено вдоль трубы по закону

Распределение скоростей частиц дается формулой

Рис. 63.1. Распределение амплитуд давлений и скоростей частиц в первых трех собственных колебаниях в трубе с обеими жесткими крышками.

На рис. 63.1 показаны распределения амплитуд давления и скорости частиц для трех первых номеров колебаний.

Частоты собственных колебаний составляют арифметическую прогрессию:

Собственное колебание наименьшей частоты называют основным тоном, колебания высших частот — обертонами. В трубе с жесткими крышками частоты обертонов относятся к частоте основного тона как целые числа; такие обертоны называют гармоническими.

Отметим весьма важное свойство так называемой ортогональности собственных колебаний:

Из свойств ортогональности и полноты набора собственных колебаний в трубе следует, что любое свободное колебание в трубе можно однозначно представить как суперпозицию собственных колебаний, взятых с теми или иными амплитудами (см. § 66).

Аналогично найдем свободные колебания и в трубе с абсолютно мягкими крышками: на крышках должны лежать узлы давления, а следовательно, вдоль трубы снова должно укладываться целое число полуволн. Соответственное условие снова имеет вид (63.1). Распределения давлений и скоростей в трубе с открытыми концами имеют вид

Распределение амплитуд давлений и скоростей частиц — такое же, как распределение амплитуд скоростей и давлений соответственно в трубе с жесткими крышками. Частоты собственных колебаний оказываются такими же, как и в трубе той же длины с жесткими крышками. Обертоны открытой трубы также гармонические. Выполняется также условие ортогональности всех собственных колебаний, и они образуют полную систему функций: других гармонических колебаний в трубе быть не может.

Рис. 65.2. То же, что на рис. 63.1, для трубы с одной жесткой и второй мягкойкрышкой.

В трубе с одной абсолютно жесткой и другой абсолютно мягкой крышкой на первой из них должна оказаться пучность, а на второй — узел давлений. Поэтому на длине трубы должно укладываться нечетное число четвертей длин волн. Это дает следующее условие для волнового числа:

Давления и скорости последовательных волн выразятся формулами

Формы первых трех колебаний показаны на рис. 63.2. Частоты последовательных волн павны

Органные трубы делают двух типов: открытые с обоих концов («открытые трубы») и открытые с одного и жестко закрытые с другого конца («закрытые трубы»). Открытый конец равносилен абсолютно мягкой крышке. Поэтому при игре на органе в «открытых» трубах возбуждается весь набор гармонических обертонов основного тона, а в «закрытых» — только нечетные обертоны. Это приводит к характерному различию тембров этих двух типов труб.

Источник

Что такое собственная частота столба воздуха в трубе

Новый Эталон Килограмма

может в ближайшее время заменить устаревший платиново-иридиевый. »»»

Солнце Становится Ближе

получены изображения высокого разрешения Солнца с космической обсерватории Solar Dynamics Observatory. »»»

Человек «Искрививший» Время

Что за Очки у Будущего?

история создания, развития и будущее популярного оптического прибора. »»»

Резонансная труба представляет собой узкую трубу, в которой создаются колебания столба воздуха. Для изменения длины столба воздуха применяются разные способы, например изменения уровня воды в трубе.

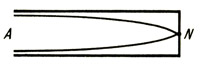
Закрытый конец трубы представляет собой узел, потому что находящийся в соприкосновении с ним воздух неподвижен. Открытый конец трубы всегда является пучностью, поскольку амплитуда колебаний здесь максимальна. На рисунке показан основной вид стоячей волны воздуха в трубе, закрытой с одного конца (закрытой трубе). Присутствует один узел и одна пучность. Длина трубы составляет примерно одну четвертую длины стоячей волны.

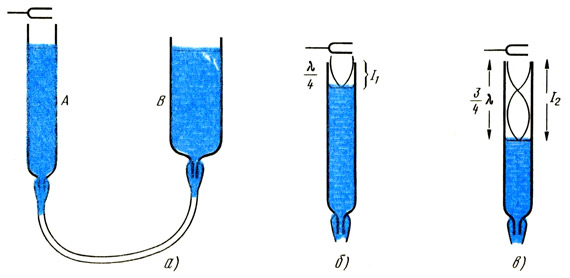
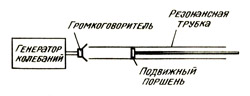
Прибор, применяемый в этом исследовании, показан на рисунке а. Резонансная труба представляет собой длинную узкую трубу А, соединенную с резервуаром В через резиновый патрубок. В обеих трубах находится вода. Когда В поднят, длина воздушного столба в А уменьшается, а когда В опускается, длина столба воздуха в А увеличивается. Поместите колеблющийся камертон сверху А, когда длина столба воздуха в А практически равна нулю. Вы не услышите никакого звука.

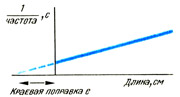
По мере увеличения длины столба воздуха в А вы услышите, как звук усиливается, достигает максимума, а затем начинает затихать. Повторите эту процедуру, регулируя В таким образом, чтобы длина воздушного столба в А давала максимальный по силе звук. Затем замерьте длину l₁ столба воздуха (рис. б).

Громкий звук слышен потому, что собственная частота столба воздуха длиной l₁ равна собственной частоте камертона, и поэтому воздушный столб колеблется в унисон с ним. Вы нашли первое положение резонанса. Фактически длина колеблющегося воздуха несколько больше столба воздуха в А.

Для того чтобы показать, что длина столба воздуха обратно пропорциональна частоте волны, нужно применить ряд камертонов. Лучше использовать маленький громкоговоритель, соединенный с откалиброванным генератором звуковой частоты, вместо камертонов фиксированной частоты. Вместо труб с водой применяется длинная труба с поршнем, поскольку это облегчает подбор длины столбов воздуха. Вблизи от конца трубы помещается постоянный источник звука, и получаются резонансные длины воздушного столба для частот 300 Гц, 350 Гц, 400 Гц, 450 Гц, 500 Гц, 550 Гц и 600 Гц.

Когда вода наливается в бутылку, образуется звук определенного тона, поскольку воздух в бутылке начинает колебаться. Высота этого тона повышается по мере уменьшения объема воздуха в бутылке. Каждая бутылка имеет определенную собственную частоту, и, когда дуешь поверх открытого горлышка бутылки, может также образоваться звук.

В начале второй мировой войны прожектора фокусировались на самолетах при помощи оборудования, работавшего в звуковом диапазоне. Чтобы не дать им сфокусироваться, некоторые экипажи выбрасывали из самолетов пустые бутылки, когда они попадали в луч прожектора. Громкие звуки падающих бутылок воспринимались приемником, и прожектора теряли фокус.

Источник

Основные теоретические сведения. Тип волн, способных распространяться в среде, зависит от упругих свойств среды

В среде могут распространяться одновременно колебания, исходящие из разных центров колебаний. Если две различные системы волн, исходящих из разных источников, перекрываются в некоторой области, а затем снова расходятся, то дальше каждая из них распространяется так, как если бы она не повстречала на своем пути другую волну.

Этот принцип независимости распространения волн известен как принцип суперпозиции, и он является весьма характерным для распространения волновых процессов,

В области перекрытия волн колебания налагаются друг на друга, происходит сложение (интерференция) волн, в результате чего колебания в одних местах получаются более сильные, а в других более слабые. Особый интерес представляет случай, когда источники колеблются с одинаковой частотой, имеют одинаковые фазы или постоянную разность фаз.

Такого рода сложение колебаний называется интерференцией от когерентных источников. Осуществить когерентные источники колебания можно, например, следующим образом. От источника распространяется сферическая волна, на пути которой поставлена преграда с двумя отверстиями , и . Согласно принципу Гюйгенса, отверстия становятся самостоятельными источниками колебаний, притом колеблющимися с одинаковой амплитудой и в одинаковых фазах.

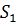
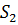
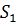
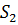
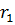
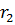
Рассмотрим результат сложения колебаний в некоторой точке А, которая отстоит от источников и на расстоянии и .

Колебания, дошедшие до точки А, выражаются соответственно следующим образом:

, (1)

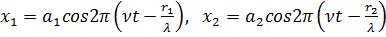
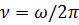
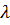
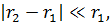
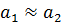
где — частота колебаний, а₁ и а₂ – амплитуды колебаний, – длина волны; т.к. то можно пренебречь затуханием и считать, что .

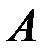
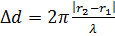
Разность фаз слагаемых колебаний в точке будет:

. (2)

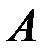
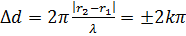
Условие максимума амплитуды в точке имеет вид:

, (3)

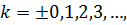
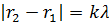
где , т.е. . Максимум амплитуды получается в точках, для которых разность хода лучей равна нулю или целому числу длин волн.

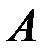
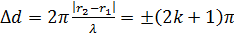
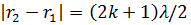
Условия минимума амплитуды в точке сводятся к требованию:

или , (4)

т.е. минимум амплитуды получается в точках, для которых разность хода лучей равна нечетному числу полуволн. Если мы наблюдаем интерференцию звуковых волн, то в точках, удовлетворяющих условию (3), амплитуда будет усиливаться, а в точках, где выполняется условие (4), ослабляться.

Особым примером результата интерференции волн служат так называемые стоячие волны, образующие в результате наложение двух встречных волн.

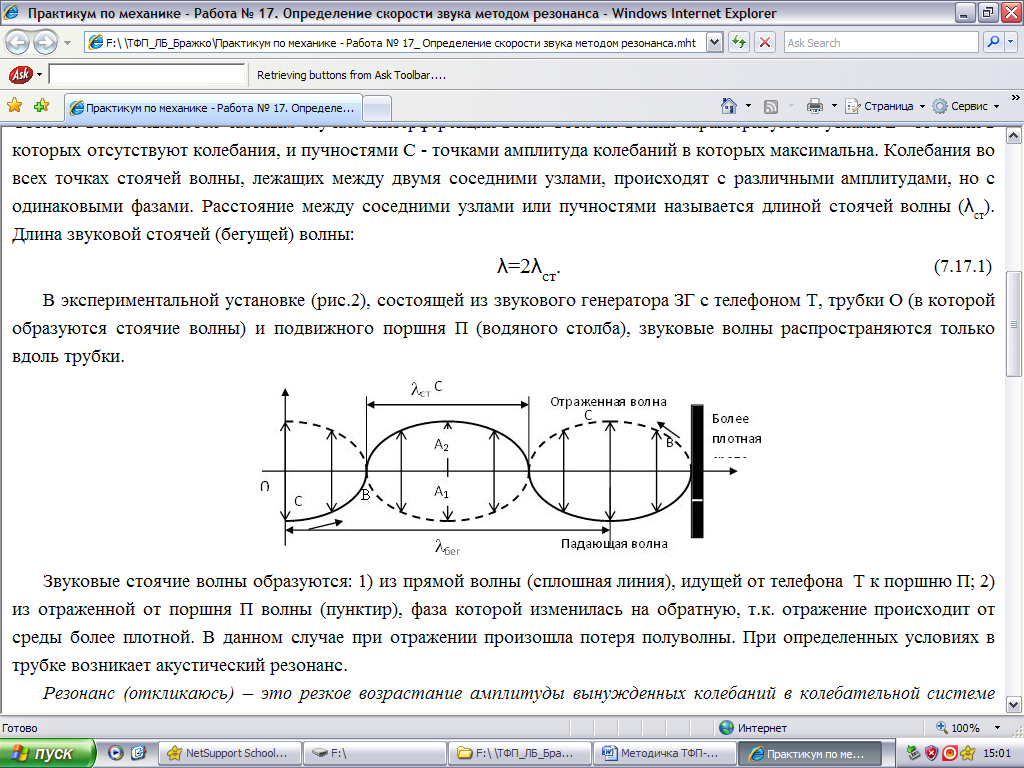
Рассмотрим распространение гармонической звуковой волны в закрепленной стеклянной трубе (рис. 1). Если на конце трубы среда более плотная, то при этом образуется отраженная волна, и наложение ее на падающую волну приводит к образованию стоячей волны. Как видно из рис.1, звуковые стоячие волны образуются: 1) из прямой волны (сплошная линия); 2) из отраженной волны (пунктир), фаза которой изменилась на обратную, т.к. отражение происходит от среды более плотной. В данном случае при отражении произошла потеря полуволны.

Рис.1. Распространение гармонической звуковой волны

в закрепленной стеклянной трубе.

Колебания во всех точках стоячей волны, лежащих между двумя соседними узлами, происходят с различными амплитудами, но с одинаковыми фазами.

Расстояние между соседними узлами или пучностями называется длиной стоячей волны (λ_ст). Как видно из рис.1, длина звуковой бегущей волны:

. (5)

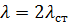
Так как частицы, находящиеся в узлах, не двигаются, то передачи энергии через узловые точки не осуществляется. Энергия не распространяется вдоль стоячей волны. Поэтому движение в стоячей волне, по существу, не является волновым движением, хотя получается в результате интерференции двух бегущих встречных волн с одинаковой частотой и амплитудой.

При определенных условиях в трубе возникает акустический резонанс.

Резонанс– это резкое возрастание амплитуды вынужденных колебаний в колебательной системе при приближении частоты внешней силы (вызывающей вынужденные колебания) к частоте какой-либо из собственных колебаний данной колебательной системы. В данном случае имеем акустический резонанс, т. е. явление, при котором колебания столба воздуха в трубе достигают максимальной амплитуды. Это происходит тогда, когда частота звуковых колебаний мембраны (внешняя, вынуждающая сила) приближается к одной из собственных частот воздушного столба в трубке. Эта частота называется резонансной частотой. При резонансной частоте звучание воздушного столба в трубе максимально.

Следует отметить, что отражение бегущих упругих волн происходит не только от вполне свободного или жестко закрепленного конца тела, но и от всякой границы, у которой изменяется свойства сплошного тела: его упругость или плотность. При этом происходит частичное отражение падающей волны, которое является причиной возникновения стоячих волн.

Если в один из концов трубы вставлен поршень, совершавший гармонические колебания, то по столбу воздуха, находящемуся внутри трубы, распространяется звуковая волна, которая по своему характеру аналогична плоской волне в свободном воздухе.

Если второй конец трубы закрыт плотной стенкой (например, заполнен водой), то звуковая волна будет отражаться от этой стенки, причем фаза деформации остается прежней, а фаза волны скоростей изменяется на величину 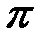. В трубе устанавливаются стоячие звуковые волны, причем на закрытом конце трубы образуется пучность деформации и узел скоростей.

На открытом конце трубы также будет происходить отражение звуковой волны, но с изменением фазы деформации на 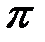— сжатие превращается в разряжение и наоборот.

Когда сжатие падающей волны подходит к отверстию трубы, частица воздуха имеет скорость, направленную в ту сторону, в которую распространяется волна. Но снаружи трубы частицы уже не вызовут такого сжатия, которое существовало в падающей волне. Поэтому частицы воздуха, вышедшие из трубы, сместятся дальше, чем смещаются частицы в трубе, и на конце трубы образуется разряжение. Точно так же, когда разряжение подходит к концу трубы, в трубу устремляются частицы воздуха из слоя, имеющего сечение больше, чем сечение трубы. Эти частицы, приобретя скорость за счет разности давлений, не только скомпенсируют разрежение в конце трубы, но и создадут в нем сжатие. Таким образом, в обоих случаях фаза деформаций изменяется на . Так как скорость частиц не изменяет знака, то энергия начнет течь в обратном направлении, т.е. у открытого конца трубы будет происходить отражение падающей волны. Следует отметить, что в случае трубы звуковая волна отчасти выходит наружу: открытый конец трубы является источником волн в окружающей среде. Отражение звуковой волны у открытого конца трубы будет тем менее заметно, чем больше диаметр трубы. Действительно, причиной отражения является выравнивание давлений в воздухе, прилегавшем к открытому концу трубы, Но так как выравнивание давлений происходит со скоростью звука, то в выравнивании давлений будут участвовать только области, отстоящие от краев трубы на расстоянии, малом по сравнению с длиной волны. Поэтому, если диаметр трубы мал по сравнению с длиной волны, то области, участвующие в выравнивании давлений, имеют размеры, сравнимые с диаметром трубы, и выравнивание давлений играет заметную роль. Если диаметр трубы превосходит длину волны, то области, участвующие в выравнивании давлений, малы, и выравнивание давлений перестает играть роль в отражении волны.

Источник