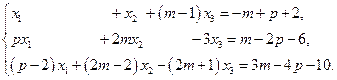Что такое собственные значения матрицы

Собственные значения и собственные векторы матрицы

Комплексное число 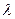называется собственным числом квадратной матрицы , если существует ненулевой вектор (матрица-столбец) , такой, что выполнено равенство

. (13)

Вектор называется в этом случае собственным вектором матрицы , соответствующим числу .

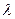
Такой собственный вектор – не единственный, т.к., если удовлетворяет уравнению (13), то и вектор — тоже удовлетворяет, где t – любое число, не равное нулю. Следовательно, собственный вектор определяется с точностью до множителя.

Матричное уравнение (13) эквивалентно однородной системе

(14)

Для того чтобы система (14) имела ненулевое решение, необходимо и достаточно, чтобы определитель этой системы был равен нулю:

(15)

Уравнение (15) называется характеристическим для матрицы и представляет собой алгебраическое уравнение — ой степени относительно . Его корни и являются собственными числами матрицы .

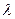
Если матрица — диагональная, т.е.

, (16)

с разными числами по диагонали ( ), то собственные числа совпадают с диагональными элементами матрицы .

Как известно из курса алгебры (см, например, ), уравнение (15) имеет, по крайней мере, один корень, а пример с матрицей (16) показывает, что у матрицы размера максимум собственных чисел. Чтобы найти собственные числа, надо решить уравнение (15). Для нахождения собственных векторов решается система (14) при найденных значениях .

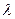
►Пример 14.Найти собственные числа матрицы .

Составим характеристическое уравнение

.

Уравнение имеет три действительных корня: , которые и являются собственными числами. ◄

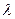
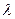
Для того чтобы найти собственный вектор, соответствующий собственному числу , надо решить систему (14), подставив в нее значение числа .

►Пример 15.Найти собственные векторыдля матрицыпримера 14.

Найдем собственный вектор для числа 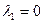. Для этого решим однородную систему

Ранг матрицы этой системы равен двум, на единицу меньше числа неизвестных. Решение найдем через миноры матрицы :

Итак, собственный вектор имеет вид , где любое число, не равное нулю. Ответ можно писать при t=1, помня замечание, приведенное выше.

Аналогично находятся два других вектора. Советуем студентам найти их самостоятельно. ◄

Упражнения.

Найти собственные числа, и для действительных собственных чисел найти собственные векторы матриц:

1) , 2) , 3) , 4) , 5) , 6) , 7) .

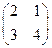
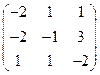
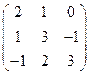
1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) .

Индивидуальное задание

1. Вычислить определители:

, , .

2. Даны матрицы:

, , , .

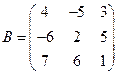
a) , где — единичная матрица.

b) (вычисления проводить, сохраняя три знака после запятой).

3. Решить матричное уравнение (найти матрицу ).

.

4.Решить системы уравнений двумя способами: по формулам Крамера и с помощью обратной матрицы.

а) б)

5.Исследовать системы уравнений и найти решение, если оно существует.

а)

б)

в)

6. Исследовать и решить системы уравнений.

а)

б)

в)

Приложение

В приложении приведены примеры работы с матрицами и примеры решения систем с использованием математического пакета MATHEMATICA Первоначально студент должен ознакомиться с работой интерфейса. Для любой работы необходимо знать операции ввода, вывода результатов; команды для выполнения операций.

Ввод данных осуществляется через знак «=». Программа подтверждает ввод строкой «In[1]:=…». Результат выполнения операции находится в строке, начинающейся словом «Out[1]=». Номера в квадратных скобках ввода и вывода совпадают.

Выполнение любой операции происходит по команде со строгим выполнением заданного формата.

Найти эти форматы можно в справке VIRTUAL BOOK. Там же приведены примеры выполнения операций. Ниже приведен ряд команд для выполнения заданий по теме.

Ввод матрицы.

Имя матрицы m1. Сама матрица вводится построчно с использование фигурных скобок.

Команда для умножении «.».

Вычисление определителя.

In[10]:= Det[m2]
Out[10]= 252

Матрица m2 введена выше.

Определение ранга матрицы.

In[18]:= MatrixRank[m1]
Out[18]= 3

Наряду со строчной записью ввода вывода использоваться записью матриц и других математических объектов в привычном виде. Для этого можно использовать команду TraditionalForm

Источник

Введение

Определения и основные факты

Если матрица не является нормальной, как, например, любая действительная несимметричная матрица, то в общем случае нельзя отыскать ортонормированный набор собственных векторов, нельзя даже гарантировать ортогональности любой пары из них (кроме редких случаев). В общем случае эти N собственных векторов будут образовывать неортогональный базис в N-мерном пространстве (но не всегда). Если собственные вектора не образуют N-мерный базис, то матрицу будем называть дефектной.

Левый и правый собственный векторы

Диагонализация матрицы

Имеется два существенно различных подхода к осуществлению указанной стратегии. Часто они хорошо работают в комбинации друг с другом, так что большинство современных методов используют оба из их. Первый подход заключается в построении индивидуальных матриц P_i как явных «элементарных» трансформаторов, расчитанных на специфические задачи, например, для обнуления конкретного внедиагонального элемента (преобразование Якоби) или целого столбца или строки (преобразования Хаусхолдера). В общем случае конечная цепочка подобных преобразований диагонализировать матрицу не может. Имеется выбор: либо использовать конечное число трансформаций для прохода большей части пути к диагонализации (например, приведя к трехдиагональной или Гессенберговской форме), а затем завершить операцию на второй стадии с помощью алгоритмов, которые будут указаны ниже. Либо итерациями свести внедиагональные элементы к пренебрежимо малым. Последний подход концептуально является простейшим и будет обсуждаться в следующем разделе, однако при N больших

10 он является примерно в 5 раз менее эффективен.

Методы факторизации также не дают сходимость за конечное число шагов. Но лучшие из них сходятся быстро и надежно, и при использовании хорошего начального состояния матрицы, первично преобразованной элементарными операциями, являются главным выбором.

Готовые прикладные пакеты для решения проблем собственных векторов и значений

Почти все готовые программы, использующиеся сейчас, восходят к алгоритмам, опубликованным в Handbook for Automatic Computation, by Wilkinson & Reinsch, Vol. II, Linear Algebra [2]. Эта великолепная подборка работ различных авторов является своего рода Библией в данной области. Общедоступным пакетом, осуществляющим алгоритмы из этой книги на Фортране, является EISPACK [3]. Программы в этой главе нашей книги являются переводами программ из Handbook или EISPACK, так что понимание приведет вас в значительной мере к пониманию того, как эти канонические пакеты составляются.

Пакеты IMSL [4] и NAG [5] также воспроизводят в основном алгоритмы из Handbook, на Фортране.

Источник

Собственный вектор

Из Википедии — свободной энциклопедии

Понятия собственного вектора и собственного числа [3] являются одними из ключевых в линейной алгебре, на их основе строится множество конструкций. Это связано с тем, что многие соотношения, связанные с линейными операторами, существенно упрощаются в системе координат, построенной на базисе из собственных векторов оператора. Множество собственных значений линейного оператора (спектр оператора) характеризует важные свойства оператора без привязки к какой-либо конкретной системе координат. По этим причинам собственные векторы имеют важное прикладное значение. Так, например, собственные векторы часто встречаются в механике, квантовой теории и так далее. В частности, оператор проекции спина на произвольную ось имеет два собственных и соответствующие им собственные векторы.

Понятие линейного векторного пространства не ограничивается «чисто геометрическими» векторами и обобщается на разнообразные множества объектов, таких как пространства функций (в которых действуют линейные дифференциальные и интегральные операторы). Для такого рода пространств и операторов говорят о собственных функциях операторов.

Множество всех собственных векторов линейного оператора, соответствующих данному собственному числу, дополненное нулевым вектором, называется собственным подпространством [4] этого оператора.

Поиск оптимальных алгоритмов вычисления собственных значений для заданного линейного оператора является одной из важных задач вычислительной математики.

Источник

Игра в собственные

Собственно, собственные

где, вспоминая правила умножения матриц ( , см. заметки ), мы воспользовались тождеством , в котором — транспонированная матрица (используем обозначения NumPy). Здесь нет проблем, но это до тех пор, пока мы работаем с действительными векторами. В комплексной области квадрат длины вектора равен скалярному произведению вектора на комплексно сопряженный. В этом случае потребуется следующая модификация соотношения (2):

Действительно, характеристическое уравнение имеет решения , где — мнимая единица. Столбцы матрицы — собственные векторы и .

Эрмитовы матрицы

Далее выполним комплексное сопряжение второго уравнения в (5)

где — эрмитово-сопряжённая матрица, элементы которой определяются как . Теперь из первого уравнения (5) вычитаем (6). В результате получим следующее замечательное выражение:

Шарль Эрмит, 1822-1901

Теперь соорудим эрмитову матрицу. Для этого сгенерируем пару случайных матриц и , затем сложим их, умножив одну из матриц на мнимую единицу , . Затем возьмем полученную матрицу и сложим ее с эрмитово-сопряженной. Действительно, , так что — эрмитова матрица.

Пришло время окунуться в мутные воды искусственного интеллекта. Внести, так сказать, свой слабый голос в общий хор.

Собственные значения (values) получились с едва заметной мнимой частью, которую мы отрезаем по идеологическим соображениям. Для этого мы оставили только действительную часть. Напомним, что

где — единичная матрица (по диагонали единицы ). Проверим в коде

Симметричный MNIST

База данных MNIST состоит тренировочного и тестового наборов, где — набор рукописных изображений цифр(матриц), которые подаем на вход, а — набор правильных ответов (числа от 0 до 9); тестовый набор выделен для удобства. Теперь посмотрим, сколько их там, и что они из себя представляют. Для этого подключим “рисовалку”.

Все выглядит замечательно, так что можно продолжать работать с нашим изображением. Тем не менее, проблемы вылазят тогда, когда мы посмотрим на матрицу, скрывающуюся под этим изображением.

Сразу можно отметить (посмотрите сами), что слишком много нулей. Это вырожденная матрица, определитель ее равен нулю.

Если попробуем вычислить собственные значения, никакого сбоя не случится, просто некоторые из них будут равны нулю.

Как видно, собственные значения находятся в комплексной области. Монтировать комплексную нейронную сеть можно, но осторожно. Основы и ссылки можно подчерпнуть из диссертации. Это отличная тема для исследований и экспериментов; советую использовать только аналитические функции, несмотря на ограничения, связанные с принципом максимума модуля (это для тех, кто в теме).

Пятерочки для закраски вполне достаточно, поскольку вероятность совпадения элементов в строке или столбце просто мизерная. Детерминант, конечно, громадный, но Python все стерпит, а пока закроем на это глаза. Если посмотрим на картинку, то поверьте, там все нормально: наша тройка практически не изменилась.

Итак, перейдем к симметричной матрице и посмотрим, что там нарисовано.

Кто скажет, что это не тройка, пусть первый бросит в меня камень! Теперь это число подготовлено для манипуляций в нейронной сети. Матрица симметричная, невырожденная, имеет замечательный набор собственных значений.

Нет слов, все работает! Итак, наши подозрения были беспочвенны, но проверять все равно надо. Теперь мы знаем, что по собственным значениям и векторам можно четко восстановить исходную матрицу. Итак, если используем обратимые операции, царапая формулы на листке бумаге, лучше проверить, как с этим обстоит дело в коде.

Эксперимент

Итак, теперь мы умеем манипулировать симметричными матрицами, используя в качестве полигона базу данных MNIST. Теперь мы попытаемся представить набор данных как симметричные матрицы, затем вычислить собственные значения, на основе которых построить нейронную сеть по примеру обращения с обычным набором. Сразу скажу, что надежд на удачный исход мало. Действительно, как мы выяснили ранее, для того чтобы восстановить матрицу собственных значений недостаточно, для этого необходим набор собственных векторов, объединенных в матрицу , которая сама по себе имеет размер исходной матрицы. Так что, с первого взгляда, мы ничего не выигрываем. Тем не менее, есть надежда, что распределение и свойства собственных значений обладают необходимыми свойствами, чтобы их классифицировать по классам. Иными словами, собственные значения несут информацию о классах рукописных цифр. Распределением собственных значений мы займемся в следующей публикации, а сейчас будем использовать наивный подход, а именно : 1) представим набор MNIST в виде симметричных матриц (28*28); 2) для каждого экземпляра вычислим собственные значения (28 штук); 3) используем Keras. Первые шаги мы уже сделали в предыдущем разделе, а над последним особо заморачиваться не будем, поскольку мы просто ставим эксперименты.

Начинаем новый блокнот:

Теперь напишем функцию, которая будет “закрашивать” матрицы из набора данных. Отмечу, что использую доморощенные функции, которые предпочитаю писать самостоятельно, чем искать на мутных форумах.

Используем эту функцию, затем масштабируем (это не обязательно).

На следующем шаге нам понадобится функция, которая делает симметричные матрицы и возвращает только собственные значения.

Включаем и смотрим.

Как видно, вполне приемлемые значения, с которыми можно и поработать. Для этого возьмем продвинутый молоток от Keras.

Пару слов напоследок

Что касается реальных, на настоящий момент, дел, то это классификация собственных значений по примеру распределения уровней сложных систем. Опять же MNIST животворящий. Но это тема следующей публикации.

Источник