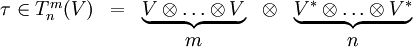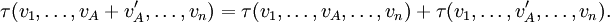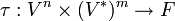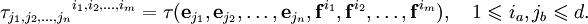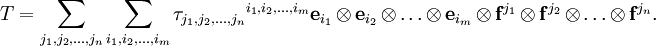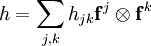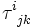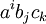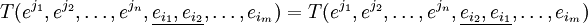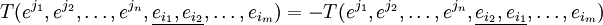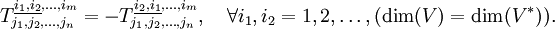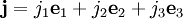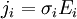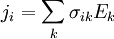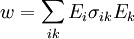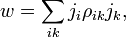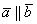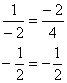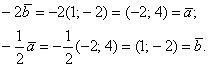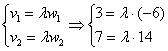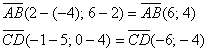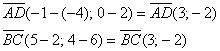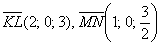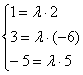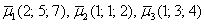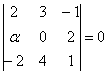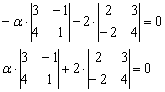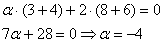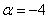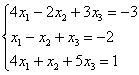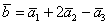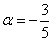Что такое собственный базис
Размерность и базис линейного пространства
Определения размерности и базиса
Базисом n-мерного линейного пространства называется упорядоченная совокупность линейно независимых векторов ( базисных векторов ).
и притом единственным образом, т.е. коэффициенты определяются однозначно. Другими словами, любой вектор пространства может быть разложен по базису и притом единственным образом.
Теорема 8.2 о дополнении системы векторов до базиса. Всякую линейно независимую систему векторов n-мерного линейного пространства можно дополнить до базиса пространства.
2. В некоторых пространствах, часто встречающихся в приложениях, один из возможных базисов, наиболее удобный с практической точки зрения, называют стандартным.
3. Теорема 8.1 позволяет говорить, что базис — это полная система элементов линейного пространства, в том смысле, что любой вектор пространства линейно выражается через базисные векторы.
5. Теорема 8.2 позволяет говорить, что базис — это максимальная линейно независимая система векторов линейного пространства, так как базис — это линейно независимая система векторов, и ее нельзя дополнить каким-либо вектором без потери линейной независимости.
Примеры базисов линейных пространств
Укажем размерность и базис для примеров линейных пространств, рассмотренных выше.
5. В пространстве матриц размеров можно выбрать 6 матриц:
которые линейно независимы. Действительно, их линейная комбинация
6. Для любого натурального в пространстве многочленов с комплексными коэффициентами можно найти п линейно независимых элементов. Например, многочлены линейно независимы, так как их линейная комбинация
Во-первых, покажем, что система линейно независима. В самом деле, возьмем линейную комбинацию этих ковекторов и приравняем ее нулевой функции
т.е. функция представлена в виде линейной комбинации функций (числа — коэффициенты линейной комбинации). Следовательно, система ковекторов является базисом сопряженного пространства и (для конечномерного пространства ).
Дуальный базис
Те́нзор — объект линейной алгебры. Частными случаями тензоров являются скаляры, векторы и билинейные формы.
Часто тензор представляют как многомерную таблицу 
Такое представление (за исключением тензоров валентности ноль — скаляров) возможно только после выбора базиса (или системы координат), при смене базиса компоненты тензора меняются определённым образом. При этом сам тензор как «геометрическая сущность» от выбора базиса не зависит. Это можно увидеть на примере вектора, являющегося частным случаем тензора: компоненты вектора меняются при смене координатных осей, но сам вектор — наглядным образом которого может быть просто нарисованная стрелка — от этого не изменяется.
Термин «тензор» также зачастую служит сокращением для термина «тензорное поле», изучением которых занимается тензорное исчисление.
Содержание
Определения
Современное определение
Сумма чисел n + m называется валентностью тензора (её также часто называют рангом). Тензор ранга (n,m) также называется n раз ковариантным и m раз контравариантным.
NB часто термином ранг пользуются как синонимом определённого здесь термина валентность. Также бывает и обратное, то есть использование термина валентность в значении ранг, определённом здесь.
Тензор как полилинейная функция
Точно так же как ковариантный тензор ранга (1,0) можно представлять как линейный функционал, тензор τ ранга (n,0) удобно представлять себе как функцию 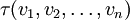
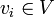
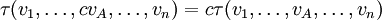
В том же ключе, тензор τ произвольного ранга (n,m) представляется полилинейным функционалом от n векторов и m ковекторов:
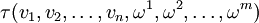
Компоненты тензора
Выберем в пространстве V базис 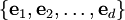
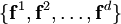
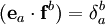
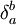
Тогда в тензорном произведении 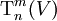
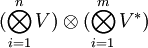

Если определить тензор как полилинейную функцию, то его компоненты определяются значениями этой функции на базисе 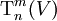
После этого тензор можно записать как линейную комбинацию базисных тензорных произведений:
Нижние индексы компонент тензора называются ковариантными, а верхние — контравариантными. Например, разложение некоторого дважды ковариантного тензора h будет таким:
О классическом определении
Так вектор (тензор первого ранга) задаётся одномерным массивом (строкой или лучше — столбцом), а такие объекты как линейный оператор и квадратичная форма — двумерной матрицей. Скаляр же (тензор нулевого ранга) задаётся одним числом (которое можно рассматривать как нульмерный массив с единственным элементом). (Скаляры и векторы удобно рассматривать в качестве частных случаев тензоров, так как все тензорные определения и теоремы для них в силе и векторы со скалярами можно при общем рассмотрении не упоминать отдельно).
Вводятся тензорные операции, которые можно считать прямым обобщением матричных операций (умножение матриц между собой и с векторами), а также векторных операций, таких, как скалярное произведение. Эти операции, если исходить из современного (аксиоматического) определения, прямо вытекают из (поли-)линейности тензоров в этом определении, после разложения векторов, свёртываемых с тензорами, по базису векторного пространства, точно так же, как и матричные операции вытекают из линейности линейных операторов и билинейных форм, представлением каждого из которых в конкретном базисе является конкретная матрица.
С помощью этих операций тензоры связываются с такими фундаментальными геометрическими объектами, как векторы и скаляры, чем, в конечном счёте, определяется их геометрический смысл. Эти же операции связывают тензоры с матрицами преобразований координат (матрицами якоби). Если речь идёт о тензорном анализе на (римановом или псевдоримановом, с которыми обычно имеют дело в классическом подходе, по крайней мере, на первом этапе) многообразии общего вида, все эти операции определяются обычно общековариантным способом (то есть способом, не зависящим от выбора криволинейных координат) с помощью метрического тензора.
Основными тензорными операциями являются сложение, в этом подходе сводящееся к покомпонентному сложению, аналогично векторам, и свёртка — с векторами, между собой и сами с собой, обобщающая матричное умножение, скалярное произведение векторов и взятие следа матрицы. Умножение тензора на число (на скаляр) можно при желании считать частным случаем свёртки, оно сводится к покомпонентному умножению.
Значения чисел в массиве, или компоненты тензора, зависят от системы координат, но при этом сам тензор, как геометрическая сущность, от них не зависит. Под проявлениями этой геометрической сущности можно понимать много что: различные скалярные инварианты, симметричность/антисимметричность индексов, соотношения между тензорами и другое. Например, скалярное произведение и длина векторов не меняется при поворотах осей, а метрический тензор всегда остаётся симметричным. Свёртки любых тензоров с самими собой и/или другими тензорами (в том числе векторами), если в результате не осталось ни одного индекса, являются скалярами, то есть инвариантами относительно замены координат: это общий способ постороения скалярных инвариантов.
При замене системы координат компоненты тензора преобразуются по определённому линейному закону.
Зная компоненты тензора в одной координатной системе, всегда можно вычислить его компоненты в другой, если задана матрица преобразования координат. Таким образом, второй подход можно суммировать в виде формулы:
тензор = массив компонент + закон преобразования компонент при замене базиса
Следует заметить, что при этом подразумевается, что все тензоры (все тензоры над одним векторным пространством), независимо от их ранга (то есть и векторы в том числе), преобразуются через одну и ту же матрицу преобразования координат (и дуальную ей, если есть верхние и нижние индексы). Компоненты тензора, таким образом, преобразуется по тому же закону, что и соответствующие компоненты тензорного произведения векторов (в количестве, равном валентности тензора), учитывая ковариантность-контравариантность компонент.
Например, компоненты тензора
преобразуется так же, как компоненты тензорного произведения трёх векторов, то есть как произведение компонент этих векторов
Так как преобразование компонент вектора известно, то таким образом можно легко сформулировать простейший из вариантов классического определения тензора.
Примеры
Как следует из определения, компоненты тензора должны меняться определённым образом синхронно с компонентами векторов того пространства, на котором он определён, при преобразовании координат. Поэтому не любая табличка или величина с индексами, выглядящая как представление тензора, на самом деле представляет тензор.
Существуют объекты, которые не только похожи на тензоры, но для которых определены (и имеют разумный и корректный смысл) тензорные операции (свёртка с другими тензорами, в частности, с векторами), однако при этом тензорами не являющиеся:
Тензорные операции
Тензоры допускают следующие алгебраические операции:
Симметрии
В различного рода приложениях часто возникают тензоры с определённым свойством симметрии.
Симметричным по двум ко-(контра-)вариантным индексам называется тензор, который удовлетворяет следующему требованию:
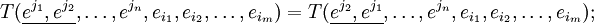
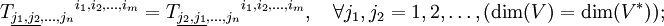
Аналогично определяется косая симметрия (или антисимметричность):
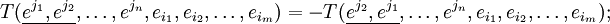
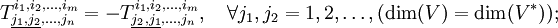
Симметрия или антисимметрия не обязательно должна охватывать только соседние индексы, она может включать в себя любые индексы, учитывая, правда, следующее: симметрия или антисимметрия может относиться только к индексам одного сорта: ко- или контравариантным. Симметрии же, смешивающие ко- и контравариантные индексы тензоров, как правило, не имеют особого смысла, так как, даже если они наблюдаются в компонентах, то разрушаются при переходе к другому базису отнесения (то есть неинвариантны).
Впрочем, в присутствии метрического тензора, наличие операций поднятия или опускания индекса устраняет это неудобство, и ограничение этим по сути снимается, когда тензор представлен подходящим образом (так, например, тензор кривизны Римана 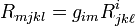
Эти определения естественным образом обобщаются на случай более чем двух индексов. При этом при любой перестановке индексов, по которым тензор является симметричным, его действие не изменяется, а при антисимметрии по индексам знак действия тензора изменяется на противоположный для нечётных перестановок (получаемых из начального расположения индексов нечётным числом транспозиций — перестановок двух индексов) и сохраняется для чётных.
Существуют и более сложные симметрии, например первое тождество Бьянки для тензора кривизны.
Тензоры в физике
В физике тензоры широко используются в теориях, обладающих геометрической природой (таких, как Общая теория относительности (ОТО)) или допускающих полную или значительную геометризацию (к каковым можно в значительной степени отнести практически все современные фундаментальные теории, поскольку они являются лоренц-ковариантными и допускают четырехмерную запись с использованием пространства Минковского, в частности, электродинамика, релятивистская механика и т. д.), а также в теории анизотропных сред (которые могут быть анизотропны изначально, как кристаллы низкой симметрии, или вследствие своего движения или напряжений, как текущая жидкость или газ, или как деформированное твердое тело). Кроме того, тензоры широко используются в механике абсолютно твердого тела.
Линейные операторы квантовой механики, конечно, также могут быть интерпретированы как тензоры над некими абстрактными пространствами (пространствами состояний), но традиционно такое применение термина тензор практически не используется, как и вообще крайне редко используется для описания линейных операторов над бесконечномерными пространствами. Вообще в физике термин тензор имеет тенденцию применяться только к тензорам над обычным физическим 3-мерным пространством или 4-мерным пространством-временем, или, в крайнем случае, над наиболее простыми и прямыми обобщениями этих пространств, хотя принципиальная возможность применения его в более общих случаях не является секретом.
Примерами тензоров в физике являются:
Нетрудно заметить, что большинство тензоров в физике (не рассматривая скаляров и векторов) имеют всего два индекса. Тензоры, имеющие большую валентность (такие, как тензор Римана в ОТО) встречаются, как правило, только в теориях, считающихся достаточно сложными, да и то нередко фигурируют в основном в виде своих свёрток меньшей валентности. Большинство симметрично или антисимметрично.
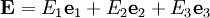
тогда можно для каждой компоненты записать:
Переходя к произвольным декартовым координатам, не совпадающим с этими выделенными направлениями, мы вынуждены будем включить матрицу поворота для преобразования координат, и поэтому в произвольной системе координат соотношение между 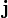
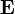
то есть тензор электропроводности будет представлен симметричной матрицей 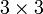
Учитывая же то, что удельная мощность тепловыделения w в проводнике равна скалярному произведению 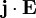
Таким образом, мы получили (правда, говоря строго, только для случая симметричного тензора) хороший наглядный геометрический образ тензора, применимый в физике. Этот образ состоит из ортогонального базиса (называемого собственным базисом тензора или его собственными координатами), ориентированного в пространстве определенным образом (определяемым свойствами среды, порождающей тензор), и трех (для трехмерного пространства) чисел (коэффициентов), связанных каждое с одной из этих осей (называемых собственными числами или собственными значениями тензора), предназначенных для умножения на них соответствующих компонент вектора, чтобы получить компоненты вектора нового. Как видим, в частном случае σ1 = σ2 = σ3 умножение на тензор σ сводится к умножению на число (на скаляр).
Или, умножая квадраты этих компонент (компонент в собственном базисе тензора) вектора на собственные числа, и сложив их, получаем скаляр. Поверхности уровня такой квадратичной формы — эллипсоиды. Такой эллипсоид служит также хорошим геометрическим образом тензора. Направление его главных осей — дает собственный базис тензора, а их величины — определяют его собственные числа.
В алгебре же всё сказанное иллюстрирует понятия собственных векторов (собственного базиса) и собственных чисел линейного оператора, квадратичной формы или матрицы, а процесс нахождения собственного базиса и собственных чисел (называемый задачей на собственные значения) называется диагонализацией оператора, квадратичной (или билинейной) формы или матрицы (так как матрица, представляющая оператор или билинейную форму становится в этом базисе диагональной).
Линейная зависимость и линейная независимость векторов.
Базис векторов. Аффинная система координат
В аудитории находится тележка с шоколадками, и каждому посетителю сегодня достанется сладкая парочка – аналитическая геометрия с линейной алгеброй. В данной статье будут затронуты сразу два раздела высшей математики, и мы посмотрим, как они уживаются в одной обёртке. Сделай паузу, скушай «Твикс»! …блин, ну и чушь спорол. Хотя ладно, забивать не буду, в конце концов, на учёбу должен быть позитивный настрой.
Линейная зависимость векторов, линейная независимость векторов, базис векторов и др. термины имеют не только геометрическую интерпретацию, но, прежде всего, алгебраический смысл. Само понятие «вектор» с точки зрения линейной алгебры – это далеко не всегда тот «обычный» вектор, который мы можем изобразить на плоскости или в пространстве. За доказательством далеко ходить не нужно, попробуйте нарисовать вектор пятимерного пространства 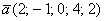
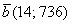
Нет, я не собираюсь грузить вас теорией, линейными векторными пространствами, задача состоит в том, чтобы понять определения и теоремы. Новые термины (линейная зависимость, независимость, линейная комбинация, базис и т.д.) приложимы ко всем векторам с алгебраической точки зрения, но примеры будут даны геометрические. Таким образом, всё просто, доступно и наглядно. Помимо задач аналитической геометрии мы рассмотрим и некоторые типовые задания алгебры. Для освоения материала желательно ознакомиться с уроками Векторы для чайников и Как вычислить определитель?
Линейная зависимость и независимость векторов плоскости.
Базис плоскости и аффинная система координат
Рассмотрим плоскость вашего компьютерного стола (просто стола, тумбочки, пола, потолка, кому что нравится). Задача будет состоять в следующих действиях:
1) Выбрать базис плоскости. Грубо говоря, у столешницы есть длина и ширина, поэтому интуитивно понятно, что для построения базиса потребуется два вектора. Одного вектора явно мало, три вектора – лишка.
2) На основе выбранного базиса задать систему координат (координатную сетку), чтобы присвоить координаты всем находящимся на столе предметам.
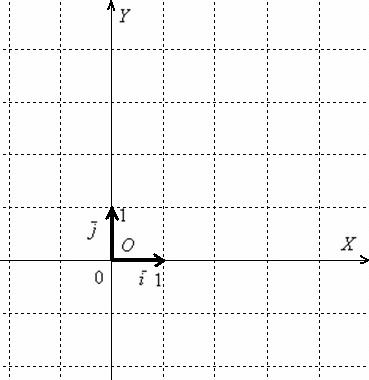
Не удивляйтесь, сначала объяснения будут на пальцах. Причём, на ваших. Пожалуйста, поместите указательный палец левой руки на край столешницы так, чтобы он смотрел в монитор. Это будет вектор 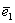
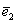
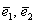
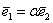
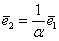
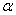
Картинку сего действа можно посмотреть на уроке Векторы для чайников, где я объяснял правило умножения вектора на число.
Будут ли ваши пальчики 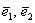
Такие векторы называют линейно зависимыми.
Справка: Слова «линейный», «линейно» обозначают тот факт, что в математических уравнениях, выражениях нет квадратов, кубов, других степеней, логарифмов, синусов и т.д. Есть только линейные (1-й степени) выражения и зависимости.
Два вектора плоскости линейно зависимы тогда и только тогда, когда они коллинеарны.
Скрестите пальцы на столе, чтобы между ними был любой угол, кроме 0 или 180 градусов. Два вектора плоскости 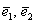
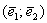
Любой вектор плоскости 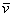
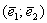
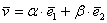
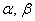
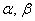
Также говорят, что вектор 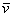
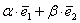
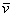
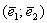
Например, можно сказать, что вектор 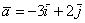
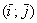
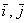
Сформулируем определение базиса формально: Базисом плоскости называется пара линейно независимых (неколлинеарных) векторов 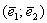
Существенным моментом определения является тот факт, что векторы взяты в определённом порядке. Базисы 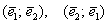
С базисом разобрались, но его недостаточно, чтобы задать координатную сетку и присвоить координаты каждому предмету вашего компьютерного стола. Почему недостаточно? Векторы являются свободными и блуждают по всей плоскости. Так как же присвоить координаты тем маленьким грязным точкам стола, которые остались после бурных выходных? Необходим отправной ориентир. И таким ориентиром является знакомая всем точка – начало координат. Разбираемся с системой координат:
Начну со «школьной» системы. Уже на вступительном уроке Векторы для чайников я выделял некоторые различия между прямоугольной системой координат и ортонормированным базисом 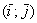
Когда говорят о прямоугольной системе координат, то чаще всего имеют в виду начало координат, координатные оси и масштаб по осям. Попробуйте набрать в поисковике «прямоугольная система координат», и вы увидите, что многие источники вам будут рассказывать про знакомые с 5-6-го класса координатные оси и о том, как откладывать точки на плоскости.
С другой стороны, создается впечатление, что прямоугольную систему координат вполне можно определить через ортонормированный базис 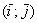
Точка 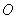
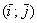
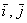
Думаю, всем понятно, что с помощью точки 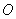
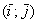
Обязаны ли координатные векторы быть единичными? Нет, они могут иметь произвольную ненулевую длину. Рассмотрим точку 
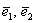
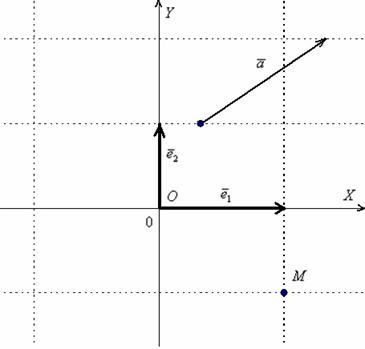
Такой базис называется ортогональным. Начало координат с векторами 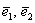
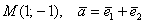
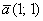
! Примечание: в ортогональном базисе, а также ниже в аффинных базисах плоскости и пространства единицы по осям считаются УСЛОВНЫМИ. Например, в одной единице по оси абсцисс содержится 4 см, в одной единице по оси ординат 2 см. Данной информации достаточно, чтобы при необходимости перевести «нестандартные» координаты в «наши обычные сантиметры».
И второй вопрос, на который уже на самом деле дан ответ – обязательно ли угол между базисными векторами должен равняться 90 градусам? Нет! Как гласит определение, базисные векторы должны быть лишь неколлинеарными. Соответственно угол может быть любым, кроме 0 и 180 градусов.
Точка 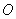
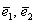
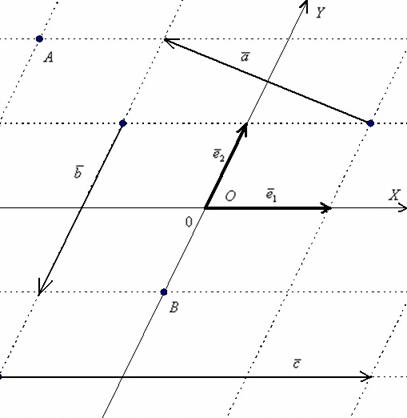
Иногда такую систему координат называют косоугольной системой. В качестве примеров на чертеже изображены точки 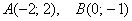
Как понимаете, аффинная система координат ещё менее удобна, в ней не работают формулы длин векторов и отрезков, которые мы рассматривали во второй части урока Векторы для чайников, многие вкусные формулы, связанные со скалярным произведением векторов. Зато справедливы правила сложения векторов и умножения вектора на число, формулы деления отрезка в данном отношении, а также ещё некоторые типы задач, которые мы скоро рассмотрим.
А вывод таков, что наиболее удобным частным случаем аффинной системы координат является декартова прямоугольная система. Поэтому её, родную, чаще всего и приходится лицезреть. …Впрочем, всё в этой жизни относительно – существует немало ситуаций, в которых уместна именно косоугольная (или какая-набудь другая, например, полярная) система координат. Да и гуманоидам такие системы могут прийтись по вкусу =)
Переходим к практической части. Все задачи данного урока справедливы как для прямоугольной системы координат, так и для общего аффинного случая. Сложного здесь ничего нет, весь материал доступен даже школьнику.
Как определить коллинеарность векторов плоскости?
Типовая вещь. Для того чтобы два вектора плоскости 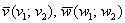
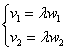
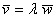
а) Проверить, коллинеарны ли векторы 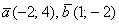
б) Образуют ли базис векторы 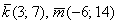
Решение:
а) Выясним, существует ли для векторов 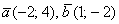
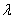
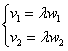
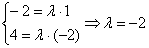
Обязательно расскажу о «пижонской» разновидности применения данного правила, которая вполне прокатывает на практике. Идея состоит в том, чтобы сразу составить пропорцию 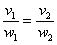
Составим пропорцию из отношений соответствующих координат векторов:
Сокращаем: 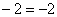
Отношение можно было составить и наоборот, это равноценный вариант:
Для самопроверки можно использовать то обстоятельство, что коллинеарные векторы линейно выражаются друг через друга. В данном случае имеют место равенства 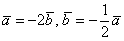
б) Два вектора плоскости образуют базис, если они не коллинеарны (линейно независимы). Исследуем на коллинеарность векторы 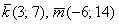
Из первого уравнения следует, что 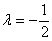
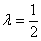
Вывод: векторы линейно независимы и образуют базис.
Упрощённая версия решения выглядит так:
Составим пропорцию из соответствующих координат векторов 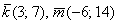
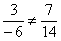
Обычно такой вариант не бракуют рецензенты, но возникает проблема в тех случаях, когда некоторые координаты равны нулю. Вот так: 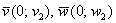
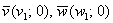
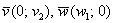
Ответ: а) 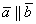
Небольшой творческий пример для самостоятельного решения:
При каком значении параметра 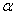
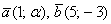
В образце решения параметр найден через пропорцию 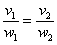
Существует изящный алгебраический способ проверки векторов на коллинеарность., систематизируем наши знания и пятым пунктом как раз добавим его:
Для двух векторов плоскости эквивалентны следующие утверждения:
1) векторы линейно независимы;
2) векторы образуют базис;
3) векторы не коллинеарны;
4) векторы нельзя линейно выразить друг через друга;
+ 5) определитель, составленный из координат данных векторов, отличен от нуля.
Соответственно, эквивалентны следующие противоположные утверждения:
1) векторы линейно зависимы;
2) векторы не образуют базиса;
3) векторы коллинеарны;
4) векторы можно линейно выразить друг через друга;
+ 5) определитель, составленный из координат данных векторов, равен нулю.
Я очень и очень надеюсь, что на данный момент вам уже понятны все встретившиеся термины и утверждения.
Рассмотрим более подробно новый, пятый пункт: два вектора плоскости 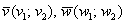
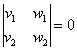
Решим Пример 1 вторым способом:
а) Вычислим определитель, составленный из координат векторов 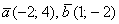
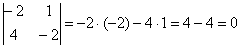
б) Два вектора плоскости образуют базис, если они не коллинеарны (линейно независимы). Вычислим определитель, составленный из координат векторов 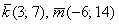
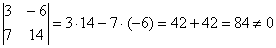
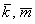
Ответ: а) 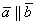
Выглядит значительно компактнее и симпатичнее, чем решение с пропорциями.
Проверка векторов на коллинеарность – простая и очень распространенная задача аналитической геометрии. Нередко в условии заодно требуется проверить векторы и на ортогональность (базис в таких случаях, как правило, ортонормированный). Данное задание подробно рассмотрено на уроке Скалярное произведение векторов.
С помощью рассмотренного материала можно устанавливать не только коллинеарность векторов, но и доказывать параллельность отрезков, прямых. Рассмотрим пару задач с конкретными геометрическими фигурами.
Даны вершины четырёхугольника 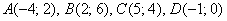
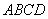
Доказательство: Чертежа в задаче строить не нужно, поскольку решение будет чисто аналитическим. Вспоминаем определение параллелограмма:
Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.
Таким образом, нужно доказать:
1) параллельность противоположных сторон 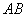
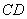
2) параллельность противоположных сторон 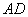
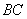
1) Найдём векторы:
Вычислим определитель, составленный из координат векторов 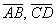
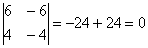
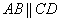
2) Найдём векторы:
Получился один и тот же вектор («по школьному» – равные векторы). Коллинеарность совсем очевидна, но решение таки лучше оформить с толком, с расстановкой. Вычислим определитель, составленный из координат векторов 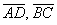
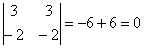
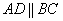
Вывод: Противоположные стороны четырёхугольника 
Больше фигур хороших и разных:
Даны вершины четырёхугольника 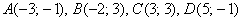
Для более строгой формулировки доказательства лучше, конечно, раздобыть определение трапеции, но достаточно и просто вспомнить, как она выглядит.
Это задание для самостоятельного решения. Полное решение в конце урока.
А теперь пора потихонечку перебираться из плоскости в пространство:
Как определить коллинеарность векторов пространства?
Правило очень похоже. Для того чтобы два вектора пространства 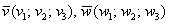
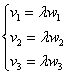
Выяснить, будут ли коллинеарны следующие векторы пространства:
а) 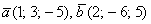
б) 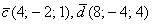
в)
Решение:
а) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов:
Система не имеет решения, значит, векторы 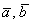
«Упрощёнка» оформляется проверкой пропорции 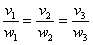
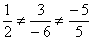
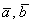
Ответ: векторы 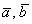
б-в) Это пункты для самостоятельного решения. Попробуйте его оформить двумя способами.
Существует метод проверки пространственных векторов на коллинеарность и через определитель третьего порядка, данный способ освещен в статье Векторное произведение векторов.
Аналогично плоскому случаю, рассмотренный инструментарий может применяться в целях исследования параллельности пространственных отрезков и прямых.
Добро пожаловать во второй раздел:
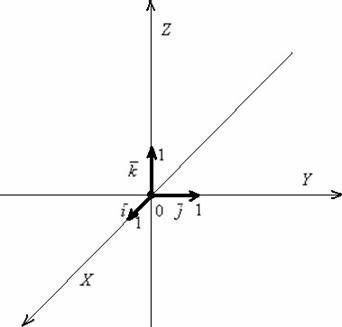
Линейная зависимость и независимость векторов трехмерного пространства.
Пространственный базис и аффинная система координат
Многие закономерности, которые мы рассмотрели на плоскости, будут справедливыми и для пространства. Я постарался минимизировать конспект по теории, поскольку львиная доля информации уже разжёвана. Тем не менее, рекомендую внимательно прочитать вводную часть, так как появятся новые термины и понятия.
Теперь вместо плоскости компьютерного стола исследуем трёхмерное пространство. Сначала создадим его базис. Кто-то сейчас находится в помещении, кто-то на улице, но в любом случае нам никуда не деться от трёх измерений: ширины, длины и высоты. Поэтому для построения базиса потребуется три пространственных вектора. Одного-двух векторов мало, четвёртый – лишний.
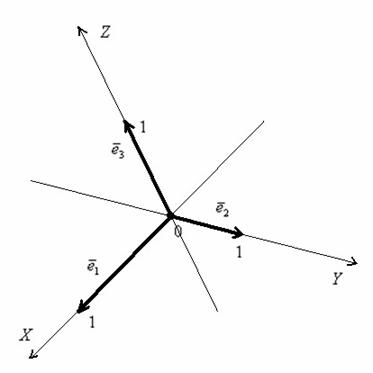
И снова разминаемся на пальцах. Пожалуйста, поднимите руку вверх и растопырьте в разные стороны большой, указательный и средний палец. Это будут векторы 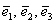
Далее зададимся важным вопросом, любые ли три вектора образуют базис трехмерного пространства? Пожалуйста, плотно прижмите три пальца к столешнице компьютерного стола. Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас пропало одно из измерений – высота. Такие векторы являются компланарными и, совершенно очевидно, что базиса трёхмерного пространства не создают.
Следует отметить, что компланарные векторы не обязаны лежать в одной плоскости, они могут находиться в параллельных плоскостях (только не делайте этого с пальцами, так отрывался только Сальвадор Дали =)).
Определение: векторы называются компланарными, если существует плоскость, которой они параллельны. Здесь логично добавить, что если такой плоскости не существует, то и векторы будут не компланарны.
Три компланарных вектора всегда линейно зависимы, то есть линейно выражаются друг через друга. Для простоты снова представим, что они лежат в одной плоскости. Во-первых, векторы 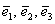
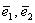
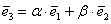
Справедливо и противоположное утверждение: три некомпланарных вектора всегда линейно независимы, то есть никоим образом не выражаются друг через друга. И, очевидно, только такие векторы могут образовать базис трёхмерного пространства.
Определение: Базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов 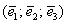
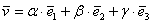
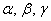
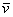
Напоминаю, также можно сказать, что вектор 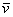
Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки и любых трёх линейно независимых векторов:
Точка 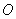
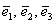
Конечно, координатная сетка «косая» и малоудобная, но, тем не менее, построенная система координат позволяет нам однозначно определить координаты любого вектора и координаты любой точки пространства. Аналогично плоскости, в аффинной системе координат пространства не будут работать некоторые формулы, о которых я уже упоминал.
Наиболее привычным и удобным частным случаем аффинной системы координат, как все догадываются, является прямоугольная система координат пространства:
Точка 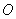
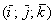
Перед тем, как перейти к практическим заданиям, вновь систематизируем информацию:
Для трёх векторов пространства эквивалентны следующие утверждения:
1) векторы линейно независимы;
2) векторы образуют базис;
3) векторы не компланарны;
4) векторы нельзя линейно выразить друг через друга;
5) определитель, составленный из координат данных векторов, отличен от нуля.
Противоположные высказывания, думаю, понятны.
Три вектора пространства 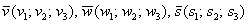
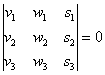
Обращаю внимание на небольшой технический нюанс: координаты векторов можно записывать не только в столбцы, но и в строки (значение определителя от этого не изменится – см. свойства определителей). Но гораздо лучше в столбцы, поскольку это выгоднее для решения некоторых практических задач.
Тем читателям, которые немножко позабыли методы расчета определителей, а может и вообще слабо в них ориентируются, рекомендую один из моих самых старых уроков: Как вычислить определитель?
Проверить, образуют ли базис трёхмерного пространства следующие векторы:
а) 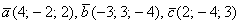
б)
Решение: Фактически всё решение сводится к вычислению определителя.
а) Вычислим определитель, составленный из координат векторов 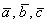
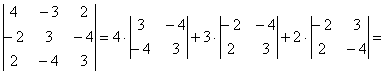
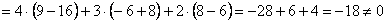
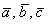
Ответ: данные векторы образуют базис
б) Это пункт для самостоятельного решения. Полное решение и ответ в конце урока.
Встречаются и творческие задачи:
При каком значении параметра 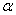
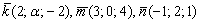
Решение: Векторы компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов равен нулю:
По существу, требуется решить уравнение с определителем. Налетаем на нули как коршуны на тушканчиков – определитель выгоднее всего раскрыть по второй строке и сразу же избавиться от минусов:
Проводим дальнейшие упрощения и сводим дело к простейшему линейному уравнению:
Ответ: при
Здесь легко выполнить проверку, для этого нужно подставить полученное значение 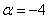
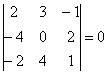
В заключение рассмотрим ещё одну типовую задачу, которая носит больше алгебраический характер и традиционно включается в курс линейной алгебры. Она настолько распространена, что заслуживает отдельного топика:
Доказать, что 3 вектора образуют базис трёхмерного пространства
и найти координаты 4-го вектора в данном базисе
Даны векторы 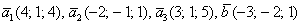
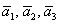
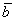
Решение: Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Какой это базис – нас не интересует. А интересует следующая вещь: три вектора 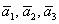
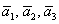
Вычислим определитель, составленный из координат векторов 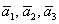
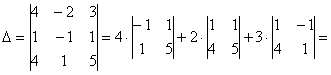
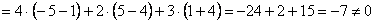
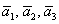
! Важно: координаты векторов 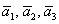
Теперь вспомним теоретическую часть: если векторы 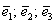
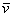
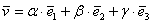
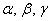
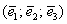
Поскольку наши векторы 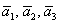
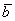
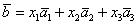
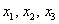
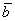
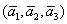
По условию и требуется найти координаты 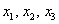
Для удобства объяснения поменяю части местами: 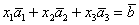
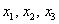
По какому принципу расставлены коэффициенты? Все коэффициенты левой части в точности перенесены из определителя 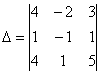
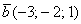
Получилась система трёх линейных уравнений с тремя неизвестными. Обычно её решают по формулам Крамера, часто даже в условии задачи есть такое требование.
Главный определитель системы уже найден: 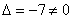
Дальнейшее – дело техники:
Таким образом:
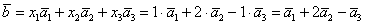
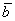
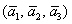
Ответ:
Более подготовленные читатели могут ознакомиться с уроком Переход к новому базису, и окончательно уяснить смысл прорешанной задачи. Кстати, с содержательной точки зрения использовать метод Крамера здесь – совсем не айс 😉
И, как я уже отмечал, задание носит алгебраический характер. Векторы, которые были рассмотрены – это не обязательно те векторы, которые можно нарисовать в пространстве, а, в первую очередь, произвольные векторы курса линейной алгебры. Для случая двумерных векторов можно сформулировать и решить аналогичную задачу – решение будет технически намного проще, и поэтому я прошёл мимо него в предыдущем параграфе.
Такая же задача с трёхмерными векторами для самостоятельного решения:
Даны векторы 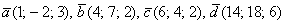
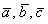
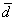
Полное решение и примерный образец чистового оформления в конце урока.
Аналогично можно рассмотреть четырёхмерное, пятимерное и т.д. векторные пространства, где у векторов соответственно 4, 5 и более координат. Для данных векторных пространств тоже существует понятие линейной зависимости, линейной независимости векторов, существует базис, в том числе, ортонормированный, разложение вектора по базису. Да, такие пространства невозможно нарисовать геометрически, но в них работают все правила, свойства и теоремы двух и трех мерных случаев – чистая алгебра.…Хотя, кто его знает, может быть и не чистая…, однако закругляемся – о философских вопросах меня уже пробивало поговорить в статье Частные производные функции трёх переменных, которая появилась раньше данного урока.
Любите векторы, и векторы полюбят вас!
Пример 2: Решение: составим пропорцию из соответствующих координат векторов: 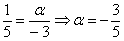
Ответ: при
Пример 4: Доказательство: трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
1) Проверим параллельность противоположных сторон 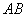
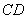
Найдём векторы: 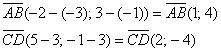
Вычислим определитель, составленный из координат векторов 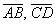
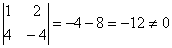
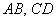
2) Проверим параллельность противоположных сторон 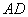
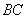
Найдём векторы: 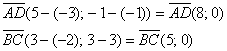
Вычислим определитель, составленный из координат векторов 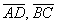
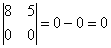
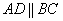
Вывод: Две стороны четырёхугольника 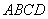
Пример 5: Решение:
б) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов: 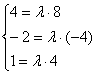
Система не имеет решения, значит, векторы 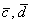
Более простое оформление:
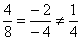
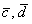
Ответ: векторы 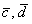
в) Исследуем на коллинеарность векторы 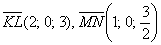
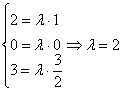
Соответствующие координаты векторов пропорциональны, значит 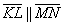
Вот здесь как раз не проходит «пижонский» метод оформления.
Ответ:
Пример 6: Решение: б) Вычислим определитель, составленный из координат векторов 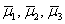
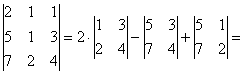
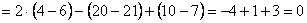
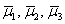
Ответ: данные векторы не образуют базиса
Пример 9: Решение: Вычислим определитель, составленный из координат векторов 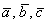

Таким образом, векторы 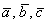
Представим вектор 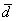
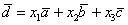
Покоординатно: 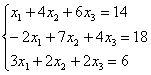
Систему решим по формулам Крамера: 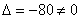
Ответ: Векторы 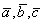
Автор: Емелин Александр
(Переход на главную страницу)