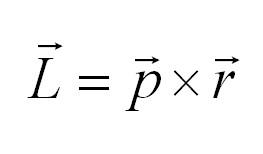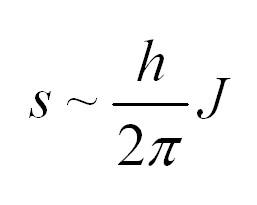Что такое собственный момент импульса

Что такое спин в физике: момент импульса, бозоны, фермионы

Итак, полностью абстрагируемся и забываем любые классические определения. Ибо спин – это понятие, присущее исключительно квантовому миру. Попробуем разобраться в том, что это такое.

Больше полезной информации для учащихся – у нас в телеграм.

Спин и момент импульса

Спин (от английского spin – вращаться) – собственный момент импульса элементарной частицы.

Теперь вспомним, что такое момент импульса в классической механике.

Момент импульса – это физическая величина, характеризующая вращательное движение, точнее, количество вращательного движения.

В классической механике момент импульса определяется как векторное произведение импульса частицы на ее радиус вектор:

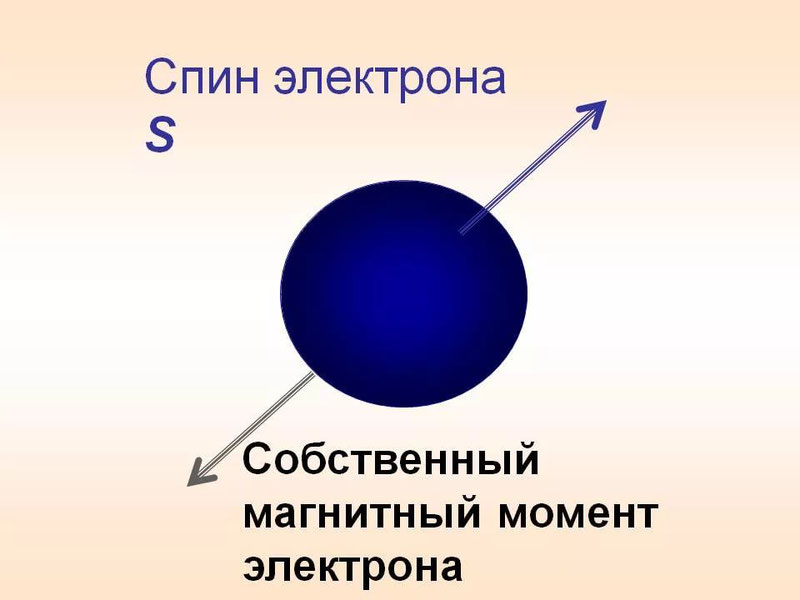
По аналогии с классической механикой спин характеризует вращение частиц. Их представляют в виде волчков, вращающихся вокруг оси. Если частица имеет заряд, то, вращаясь, она создает магнитный момент и явлеятся своего рода магнитом.

Однако данное вращение нельзя трактовать классически. Все частицы помимо спина обладают внешним или орбитальным моментом импульса, характеризующим вращение частицы относительно какой-то точки. Например, когда частица движется по круговой траектории (электрон вокруг ядра).

Спин же является собственным моментом импульса, то есть характеризует внутреннее вращательное состояние частицы вне зависимости от внешнего орбитального момента импульса. При этом спин не зависит от внешних перемещений частицы.

Представить, что же там вращается внутри частицы, невозможно. Однако факт остается фактом – для заряженных частиц с разнонаправленными спинами траектории движения в магнитном поле будут различны.

Спиновое квантовое число

Для характеристики спина в квантовой физике введено спиновое квантовое число.

Спиновое квантовое число – одно из квантовых чисел, присущих частицам. Часто спиновое квантовое число называют просто спином. Однако следует понимать, что спин частицы (в понимании собственного момента импульса) и спиновое квантовое число – это не одно и то же. Спиновое число обозначается буквой J и принимает ряд дискретных значений, а само значение спина пропорционально приведенной постоянной Планка:

Бозоны и фермионы

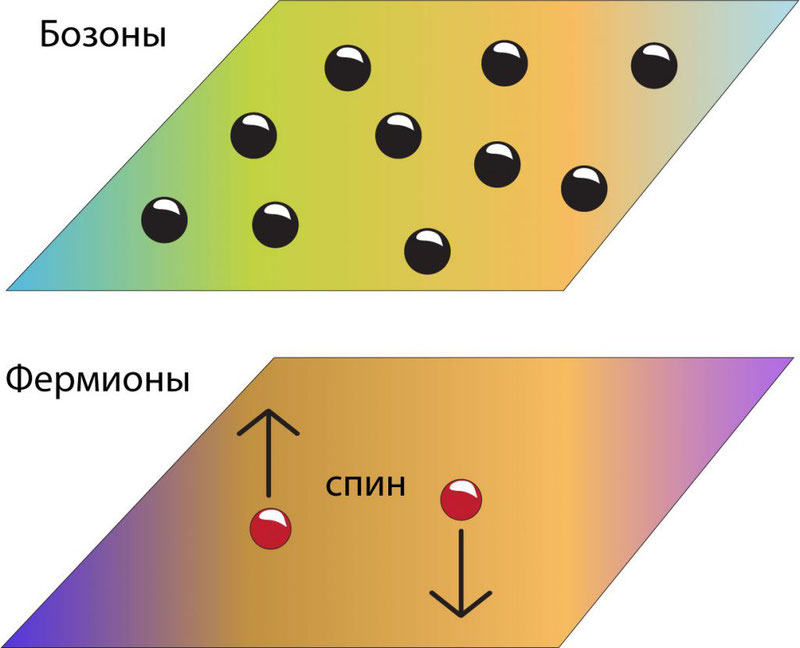
Разным частицам присущи разные спиновые числа. Так, главное отличие состоит в том, что одни обладают целым спином, а другие – полуцелым. Частицы обладающие целым спином называются бозонами, а полуцелым – фермионами.

Бозоны подчиняются статистике Бозе-Эйнштейна, а фермионы – Ферми-Дирака. В ансамбле частиц, состоящем из бозонов, любое их количество может находиться в одинаковом состоянии. С фермионами все наоборот – наличие двух тождественных фермионов в одной системе частиц невозможно.

Фермионы: электрон, лептон, кварк

Попробуем представить, чем отличаются частицы с разными спиновыми числами на примерах из макромира. Если спин объекта равен нулю, то его можно представить в виде точки. Со всех сторон, как ни вращай этот объект, он будет одинаков. При спине равном 1 поворот объекта на 360 градусов возвращает его в состояние, идентичное первоначальному состоянию.

Надеемся, что вы осилите эту теорию быстро и сможете при случае применить знания на практике. Ну а если задачка по квантовой механике оказалось непосильно сложной или не можете не забывайте о студенческом сервисе, специалисты которого готовы прийти на выручку. Учитывая, что сам Ричард Фейнман сказал, что «в полной мере квантовую физику не понимает никто», обратиться за помощью к опытным специалистам – вполне естественно!

Источник

Момент импульса

Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения.

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях).

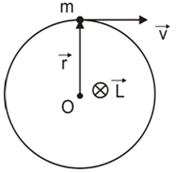
Моментом импульса L материальной точки относительно произвольной точки О называется физическая величина, определяемая векторным произведением радиус-вектора r этой материальной точки, проведенного из точки О, на величину ее импульса Р(рис. 6):

(Дж•с),

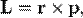
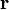
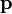
где – радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, – импульс частицы.

Если твердое тело, вращающееся вокруг некоторой неподвижной оси z, представить в виде совокупности элементарных масс, и спроектировать моменты импульсов всех этих элементарных масс на это направление, получим момент импульса тела L_z относительно этой оси (L_z – скалярная величина).

В случае тела, вращающегося вокруг оси симметрии, векторы L и ω имеют одинаковое направление и тогда:

= I .(1)

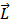
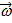
Продифференцируем выражение (1) по времени:

Таким образом, производная по времени от момента импульса твердого тела относительно оси вращения равна моменту сил относительно той же оси:

dL/ dt = M (3)

Из уравнения (3) видно, что если момент внешних сил, действующих на тело, равен нулю, то момент импульса тела остается постоянным.

Если M = 0, то: dL/dt = 0 ⇒ L = const. (4)

Выражение (4) представляет собой закон сохранения момента импульса:

момент импульса замкнутой системы тел не меняется со временем, причем это утверждение справедливо для момента импульса, взятого относительно любой точки инерциальной системы отсчета. Этот закон выполняется только в инерциальных системах отсчета.

Закон сохранения момента импульса – фундаментальный закон природы. Он связан со свойством симметрии пространства – его изотропностью, т.е. с инвариантностью физических законов относительно поворота замкнутой системы в пространстве на любой угол.

Источник

Момент импульса

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Пожалуй, наибольшую роль, момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях).

Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр.

Момент импульса замкнутой системы сохраняется. Момент импульса является одним из трёх аддитивных (энергия, импульс, момент импульса) интегралов движения.

Связанные понятия

Упоминания в литературе

Связанные понятия (продолжение)

Эта статья — об энергетическом спектре квантовой системы. О распределении частиц по энергиям в излучении см. Спектр, Спектр излучения. Об энергетическом спектре сигнала см. Спектральная плотность.Энергетический спектр — набор возможных энергетических уровней квантовой системы.

В теории поля представление системы зарядов в виде некоторых квадрупо́лей, аналогично представлению её в виде системы диполей, используется для приближённого расчёта создаваемого ей поля и излучения. Более общим представлением является разложение системы на мультиполи, соответствующее разложению потенциалов в ряд Тейлора по некоторым переменным. Квадруполь — частный случай мультиполя. Квадрупольное рассмотрение системы оказывается особенно важным в том случае, когда её дипольный момент и заряд равны.

Источник

Момент импульса

Импульс материальной точки есть произведение ее массы на скорость:

Аналогом импульса во вращательном движении является момент импульса, который является произведением момента инерции материальной точки на ее угловую скорость:

Момент импульса является векторной величиной, по направлению совпадает с направлением вектора угловой скорости.

Закон сохранения момента импульса

Момент импульса сохраняется в случае, если сумма всех моментов внешних сил равна нулю.

Наглядное использование момента импульса можно видеть во время выступления фигуристов, когда они начинают вращение с широко раставленными в стороны руками, постепенно смыкая руки, они увеличивают скорость своего вращения. Таким образом, они уменьшают свой момент инерции и увеличивают свою угловую скорость вращения. Таким образом, зная начальную угловую скорость вращения ω₀ и его момент инерции с разведенными I₀ и сомкнутыми руками I₁, используя закон сохранения момента импульса, можно найти конечную угловую скорость ω₁:

Применяя закон сохранения импульса, можно достаточно просто рассчитывать параметры орбитального движения планет и космических аппаратов.

Согласно закону сохранения импульса, имеем следующе равенства:

Поскольку диаметр Луны (3476 км) мал по сравнению с расстоянием до Земли, будем считать Луну материальной точкой, что значительно упростит расчеты, не оказав существенного влияния на их точность.

Моменты инерции для материальной точки будут равны:

Проведем соответствующие подстановки в формулу закона сохранения импульса:

Выполнив несложные алгебраичиские преобразования, получим:

Подставляем числовые значения:

Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:

Код кнопки:
Политика конфиденциальности Об авторе

Источник

Савельев И.В. Курс общей физики, том I

Загрузить всю книгу

Титульный лист

Главная редакция физико-математической литературы

Механика, колебания и волны,

КУРС ОБЩЕЙ ФИЗИКИ, ТОМ I

Главная цель книги — познакомить студентов прежде всего с основными идеями и методами физики. Особое внимание обращено на разъяснение смысли физических законов и на сознательное применение их. Несмотря на сравнительно небольшой объем, книга представляет собой серьезное руководство, обеспечивающее подготовку, достаточную для успешного усвоения в дальнейшем теоретической физики и других физических дисциплин.

Предисловие к четвертому изданию

При подготовке к настоящему изданию книга была значительно переработана. Написаны заново (полностью или частично) параграфы 7, 17, 18, 22, 27, 33, 36, 37, 40, 43, 68, 88. Существенные добавления или изменения сделаны в параграфах 2, 11, 81, 89, 104, 113.

Ранее, при подготовке ко второму и третьему изданиям были написаны заново параграфы 14, 73, 75. Существенные изменения или добавления были внесены в параграфы 109, 114, 133, 143.

Таким образом, по сравнению с первым изданием облик первого тома заметно изменился. Эти изменения отражают методический опыт, накопленный автором последние десять лет преподавания обшей физики в Московском инженерно-физическом институте.

Ноябрь 1969 г. И. Савельев

Из предисловия к четвертому изданию

Предлагаемая вниманию читателей книга представляет собой первый том учебного пособия по курсу общей физики для втузов. Автор в течение ряда лет преподавал общую физику в Московском инженерно-физическом институте. Естественно поэтому, что пособие он писал имея в виду прежде всего студентов инженерно-физических специальностей втузов.

При написании книги автор стремился познакомить учащихся с основными идеями и методами физической науки, научить их физически мыслить. Поэтому книга не является по своему характеру энциклопедичной, содержание в основном посвящено тому, чтобы разъяснить смысл физических законов и научить сознательно применять их. Не осведомленности читателя по максимально широкому кругу вопросов, а глубоких знаний фундаментальным основам физической пауки — вот что стремился добиться автор.

Источник