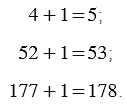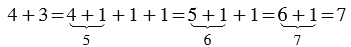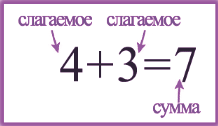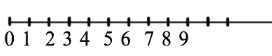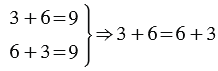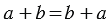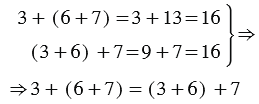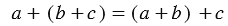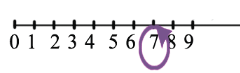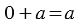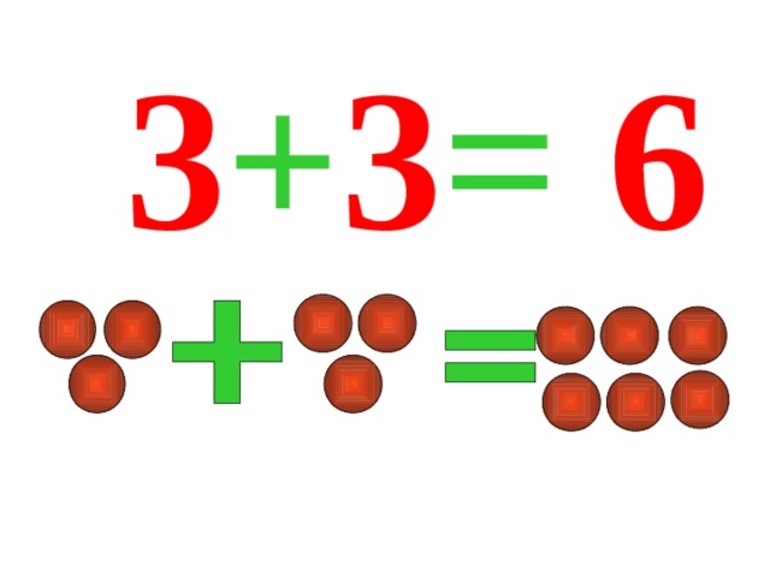Что такое сочетать сильное свойство сложения
Свойства сложения
Содержание
Мы уже умеем складывать числа с помощью рисунка и координатного луча. Умеем складывать однозначные числа, такие как 7 и 5, и многозначные, такие как 123 и 456.
Для того чтобы складывать числа было легче, существует несколько простых правил. Их еще называют законами сложения или свойствами.
Закон – это что-то, что никогда не меняется, и что можно применять для всех чисел.
Заучивать законы сложения не нужно, их нужно только один раз понять и научиться использовать в примерах и задачах. Сделать это очень просто. Сейчас мы сможем в этом убедиться.
Переместительное свойство
Первый закон сложения называется переместительным законом сложения. Звучит он так:
От перестановки слагаемых сумма не меняется.
Чтобы понять этот закон, мы решим один и тот же пример двумя способами.
А теперь поменяем наши числа местами и посчитаем ответ:
Результаты сложения получились одинаковыми. Но заметим, что во втором случае посчитать было гораздо проще, не так ли? Значит, проще было поменять числа местами и потом посчитать.
Сложение с нулем
В корзине было 100 яблок, туда положили 0 яблок, сколько яблок стало в корзине?
Очевидно, что если в корзину не положили яблок, то количество яблок в ней не изменилось, то есть по-прежнему равно 100.
От прибавления нуля число не изменяется
$10+0 = 10$
$0 + 8 = 8$
$0 + 0 = 0$
Сочетательное свойство
В некоторых примерах бывает нужно сложить не два числа, а несколько.
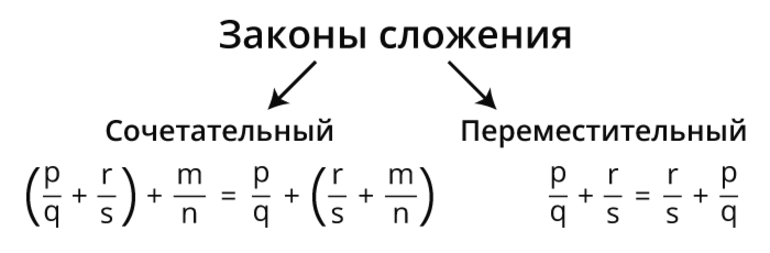
Складываем все числа слева направо привычным для нас способом. Получаем:
Если мы внимательно посмотрим на числа, то сможем увидеть, что легче сначала сложить 4 и 6, а затем к полученной сумме прибавить и число 29.
$29 + 4 + 6 = 24 + 10 = 39$
Ответ получился таким же.
Значит, при сложении нескольких чисел можно складывать сначала те числа, которые нам удобнее сложить. А затем уже к полученной сумме прибавляем оставшиеся числа. Мы, так сказать, сочетаем те числа, которые легче посчитать при сложении.
Этот закон называется сочетательный закон сложения. Кратко он звучит так:
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.
Законы сложения можно применять при сложении не только двух или трех, но и большего количество чисел.
Чтобы решить этот пример, посмотрим внимательно на числа. Заметим, что легче всего было бы сложить 128 и 12, а к числу 383 легче прибавить 17. Поэтому мы сейчас поменяем местами числа 17 и 12. То есть применим в нашем примере переместительный закон. Получим:
Теперь группируем попарно числа, которые будем складывать. То есть применим сочетательный закон. Для этого мы используем скобки:
Считаем, сколько получится в скобках и складываем результаты:
Вот так легко и быстро мы получили ответ, применяя законы сложения.
Свойства сложения и вычитания
Свойства (или законы) арифметических действий на числовых примерах мы рассматривали в теме «Законы арифметики» для начальной школы.
В 5 классе законы арифметики записываются с помощью буквенных выражений. Поэтому теперь мы рассмотрим эти и другие свойства в виде буквенных выражений.
Свойства сложения
Переместительное свойство сложения
От перестановки слагаемых сумма не меняется.
В буквенном виде свойство записывается так:
Сочетательное свойство сложения
Чтобы к сумме двух чисел прибавить третье число можно к первому числу прибавить сумму второго и третьего числа.
Так как результат сложения трёх чисел не зависит от того как поставлены скобки, то скобки можно не ставить и писать просто « a + b + с ».
Переместительное и сочетательное свойство сложения позволяют сформулировать правило преображения сумм.
При сложении нескольких чисел их можно как угодно объединять в группы и переставлять.
Свойство нуля при сложении
Сумма двух натуральных чисел всегда больше каждого из слагаемых. Но это не так, если хотя бы одно из слагаемых равно нулю.
Если к числу прибавить нуль, получится само число.
Свойства вычитания
Свойство вычитания суммы из числа
Чтобы вычесть сумму из числа, можно из него вычесть одно слагаемое и затем из результата вычесть другое слагаемое.
Скобки в выражении « (a − b) − c » не имеют значения и их можно опустить.
Свойство вычитания числа из суммы
Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.
Свойство нуля при вычитании
Если из числа вычесть нуль, получится само число.
Если из числа вычесть само число, то получится нуль.
Сложение натуральных чисел
К нескольким натуральным числам прибавим 1:
Мы видим, что когда мы прибавляем к натуральному числу 1, получаем следующее за ним натуральное число, т.е. следующее число больше предыдущего на единицу. Теперь к 4 прибавим 3: 4+3: для этого к 4 прибавим 3 раза единицу. Учитывая, что при прибавлении к числу единицы получаем следующее число, получим:
Но мы записываем коротко: 4+3=7.
Числа, которые складываются, называются слагаемыми, число, которое получается в результате сложения, называется суммой.
Сложение чисел на координатном луче
Изобразим координатный луч. Отметим на нем начало координат, единичный отрезок и несколько чисел, следующих друг за другом:
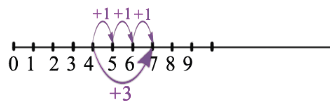
Рассмотрим наш пример: 4+3. Для того чтобы к 4 прибавить 3 на координатном луче, необходимо от точки 4 вправо отложить 3 единичных отрезка:
И мы попадем в точку 7, следовательно 4+3=7.
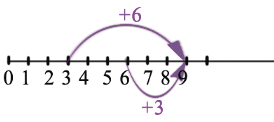
Теперь попробуем отложить на луче, от точки 3 6 единичных отрезков, и от точки 6 3 единичных отрезка, другими словами к 3 прибавим 6 и к 6 прибавим 3 :
Мы видим, что и в первом и во втором случае мы попадаем в одну и ту же точку: 9, следовательно сумма чисел 3 и 6 и 6 и 3 одинакова и равна 9. Это можно записать с помощью равенства:
В этом случае мы меняем местами слагаемые и получаем первое свойство сложения — переместительное свойство :
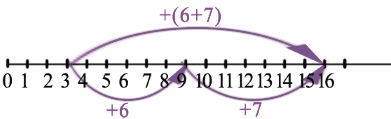
Рассмотрим с помощью координатного луча следующие суммы: 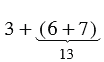
Заметим, что и в первом и во втором случае мы попадаем в одну точку: 16. Это можно записать равенством:
К натуральному числу можно прибавлять не только натуральное число, но еще и нуль, изобразим на луче прибавление нуля к 7:
Свойства сложения
От перестановки слагаемых сумма не меняется
Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом к полученной сумме прибавить второе слагаемое
Если прибавить к нулю какое-нибудь число, то получится прибавленное число
Сравнение сумм натуральных чисел
Сравним (15+81) и (15+77), для этого рассмотрим слагаемые этих двух сумм: Мы видим, что первые слагаемые у них одинаковые, поэтому переходим к сравнению вторых слагаемых: 81 >77, поэтому (15+81)>(15+77).
Теперь сравним (21+15) и (34+54), для этого опять рассмотрим слагаемые, в данном случае одинаковых у нас нет, но мы видим, что слагаемые первой суммы меньше слагаемых второй суммы, а значит мы можем записать: (21+15) При увеличении слагаемых сумма увеличивается, а при уменьшении уменьшается.
Письменный прием сложения («сложение в столбик»)
Часто при решении задач, нам необходимо складывать многозначные числа, поэтому считать в «уме» или чертить координатный луч не целесообразно, для решения таких задач был придуман письменный прием сложения или «сложение в столбик», который помогает сложение многозначных чисел свести к сложению однозначных чисел, которое мы можем производить легко. Рассмотрим пример:
| 1 | 1 | 1 | |||
| + | 4 | 5 | 8 | 7 | 1 |
| 4 | 3 | 8 | 2 | ||
| 5 | 0 | 2 | 5 | 3 |
Вывод: Если при сложении чисел одного разряда число получается больше или равное 10, то 1 десяток записываем над следующим разрядом, а единицы под рассматриваемым разрядом.
Поделись с друзьями в социальных сетях:
Общие сведения
Сложение является одной из базовых арифметических операций в математике. Оно изучается во втором классе общеобразовательной школы. Существует всего 2 правила: переместительный и сочетательный закон сложения. Однако многие ученики часто их путают. Разобраться в этом помогут специалисты. Они разработали специальную методику, позволяющую быстро запомнить различие между ними.
Однако для изучения алгоритма нужно знать базовые термины и определения. К ним относятся:
Сложение состоит минимум из трех элементов: двух слагаемых (одно из них увеличивается на другое) и результата. Последний называется суммой. На примере это выглядит так: 5+9=14, где 5 — I слагаемое, 9 — второй элемент-слагаемое или число, на которое нужно увеличить первое слагаемое, а 14 — их сумма.
Переместительное правило
Переместительное (коммутативное) правило является очень простым для понимания. Оно формулируется следующим образом: если поменять местами слагаемые, их сумма не изменится. Математическая форма записи закона выглядит следующим образом: q+w=s.
На практическом примере правило реализуется в таком виде: 5+6=6+5=11. Последнее числовое выражение очень легко проверить. Для этого достаточно воспользоваться обыкновенным калькулятором. При сложении 5 и 6 он покажет величину, равную 11. Следует отметить, что таким образом и доказывается закон переместительного свойства сложения.
Прием практической реализации для доказательства правил и утверждений применяется очень часто. Это и есть оптимальная методика, позволяющая выяснить работоспособность того или иного утверждения. Далее необходимо рассмотреть сочетательный закон сложения.
Сочетательный закон
Сочетательное правило сложения возможно применить, когда числовое выражение включает в свой состав от трех и более слагаемых. Сочетательный закон сложения во 2 классе можно сформулировать следующим образом: слагаемые, входящие в состав выражения, можно для удобства складывать в любом порядке.
Очень часто правило называют ассоциативным свойством операции сложения. Ее математическая запись имеет такой вид: p+r+s=(p+s)+r=(s+r)+p=z. Чтобы доказать утверждение, нужно решить пример «2+9+8+1». Его специалисты рекомендуют решать по такому алгоритму:
К сочетательному свойству также можно применить и переместительное (коммуникативное) правило. Этим приемом очень часто пользуются специалисты. Кроме того, по-другому ассоциативный закон называется методом группировки чисел. Далее нужно рассмотреть методику применения двух законов на практике.
Методика применения
Методика использования правил сложения зависит от конкретного примера. Однако специалисты рекомендуют придерживаться следующего алгоритма нахождения результатов числовых выражений:
Сочетание элементов можно выполнять несколько раз, т. е. вычислить сначала одно значение, а потом опять перегруппировать выражение. Перемену мест слагаемых можно производить в несколько заходов.
Кроме того, законы сложения можно применять не только для целых чисел, но и для дробных. Для совершенствования качества усвоения теоретического материала рекомендуется придумать примеры и решить их.
Некоторые ученики часто путают принадлежность распределительного правила к суммации двух и более величин. Этого делать не нужно, а требуется запомнить, что у сложения только 2 закона, но не 3. Последний принадлежит только операциям деления и умножения.
Переместительное и сочетательное свойства можно применять и для вычитания. Далее необходимо на практическом примере разобрать использование правил сложения и методику их применения.
Пример решения
Для закрепления теоретического материала необходимо решить следующий пример: 4+9+6+5+1+15+17+2+12+1. Находится решение по такому алгоритму:
Следует учитывать, что группировку элементов можно выполнять в произвольном порядке и количестве. Суть метода — достижение максимальной скорости вычислений при сложении простых элементов, позволяющих без проблем произвести расчеты.
Если сразу выполнить расчеты сложно, рекомендуется группировать числа по количеству знаков, т. е. однозначные с однозначными, двузначные с двузначными и т. д.
Таким образом, сочетательный и переместительный законы применяются в математике для ускорения вычислений.
Сочетательный закон сложения – правило
Многие ученики путают понятия сочетательного закона сложения и сочетательного свойства сложения. Насколько это допустимо и как не путаться – разберемся вместе.
Сумма чисел
Сначала вспомним, что такое сумма чисел. Если два числа разбить на единицы, а потом все эти единицы свести в одно число, то получится сумма. Примерно так объясняют сумму в младших классах, иногда приводя примеры на сложение фруктов, конфет или канцелярских принадлежностей.
Такие объяснения правильны, но они не подходят для курса средней школы. Чем старше ученик, тем более глубокое и емкое определение ему нужно знать.
Поэтому в математике старших классов используют другое определение. Сумма это движение числа по числовой прямой вправо. На самом деле, число может двигаться и влево, при сложении отрицательных чисел. Но принято говорить «вправо», поскольку такие суммы сначала преобразовываются в разность
Законы сложения
Законов сложения всего два. Это сочетательный и переместительный. Сочетательный закон гласит, если в примере есть несколько слагаемых, то можно сложить два из них между собой, а потом к результату прибавить оставшееся слагаемое. Таким образом, можно складывать сколько угодно большие выражения. Применение этого свойства основано на сочетании слагаемых, откуда и взято это название.
Переместительный закон имеет следующую формулировку: «От перемены мест слагаемых сумма не меняется». Вне зависимости от того, как расположены слагаемые в примере, итоговое значение не измениться. Если подумать, то это логично. Какая разница, высыпать в корзину 10 фруктов, а потом еще 8 или сначала 8, а потом 10.
Разве количество фруктов в корзине от этого измениться? Конечно, нет.
Свойства сложения – это проявление простейшей логики в математике. Они доказывались опытным путем еще математиками Древней Греции. На сегодняшний день кажется невозможным не использовать их, поэтому свойства нужны скорее не для использования и запоминания, а для теоретического подтверждения того, что все и так знают. Ведь всеобщее знание это не аргумент в математике всегда нужно ссылаться на какие-то законы, аксиому и теоремы, чтобы доказать правильность решения. При этом свойство и закон сложения это одно и то же. Никакой разницы между ними нет.
Сочетательный закон
Сочетательный закон интересен тем, что может значительно ускорить выполнение сложения. Рассмотрим некоторые принципы быстрого счета, основанные на сочетательном законе.
3,72-5+5,28+17,8+9,2 – иногда проще разделить целые и дробные части дробей, чтобы ускорить счет.
Что мы узнали?
Мы поговорили о том, что такое сумма. Узнали о двух основных свойствах сложения и выделили правило сочетательного закона сложения. Привели несколько способов быстрого счета, основанных на сочетательном законе сложения. Рассмотрели несколько простых примеров.