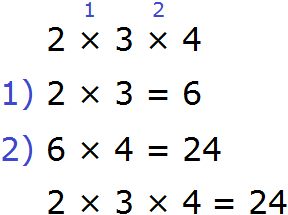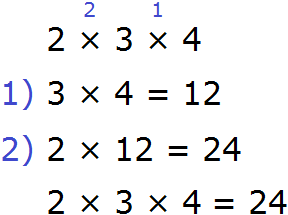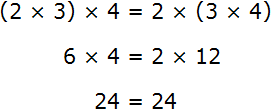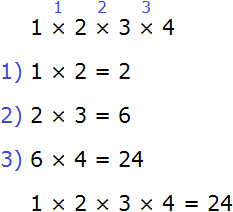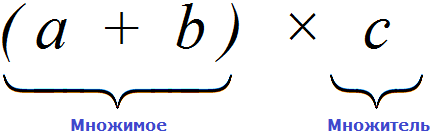Что такое сочетательное свойство сложения и умножения
Свойства умножения
Переместительное свойство умножения
От перестановки сомножителей местами произведение не меняется.
Следовательно, для любых чисел a и b верно равенство:
выражающее переместительное свойство умножения.
4 · 2 · 3 = 3 · 2 · 4 = 24.
Обратите внимание, что данное свойство можно применять и к произведениям, в которых более двух множителей.
Сочетательное свойство умножения
Результат умножения трёх и более множителей не изменится, если какую-либо группу множителей заменить их произведением.
Следовательно, для любых чисел a, b и c верно равенство:
выражающее сочетательное свойство умножения.
3 · 2 · 5 = 3 · (2 · 5) = 3 · 10 = 30
3 · 2 · 5 = (3 · 2) · 5 = 6 · 5 = 30.
Сочетательное свойство используется для удобства и упрощения вычислений при умножении. Например:
25 · 15 · 4 = (25 · 4) · 15 = 100 · 15 = 1500.
В данном случае можно было вычислить всё последовательно:
25 · 15 · 4 = (25 · 15) · 4 = 375 · 4 = 1500,
но проще и легче сначала умножить 25 на 4 и получить 100, а уже потом умножить 100 на 15.
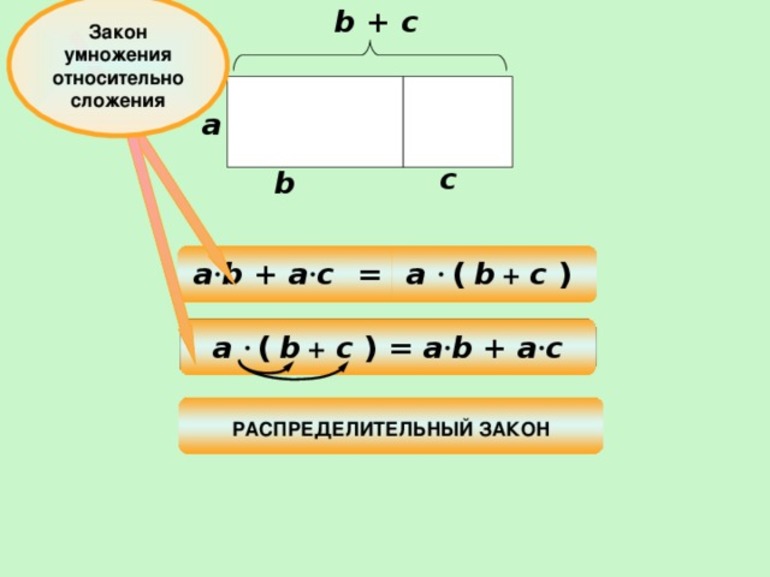
Распределительное свойство умножения
Сначала рассмотрим распределительное свойство умножения относительно сложения:
Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
выражающее распределительное свойство умножения.
Так как в данном случае число и сумма являются множителями, то, поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на это число и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
Теперь рассмотрим распределительное свойство умножения относительно вычитания:
Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
Так как в данном случае число и разность являются множителями, то поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы разность чисел умножить на число, можно уменьшаемое и вычитаемое отдельно умножить на это число и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
Переход от умножения:
соответственно к сложению и вычитанию:
называется раскрытием скобок.
Переход от сложения и вычитания:
называется вынесением общего множителя за скобки.
Свойства умножения и деления
Свойства умножения
Переместительное свойство умножения
От перестановки множителей произведение не меняется.
Сочетательное свойство умножения
Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
Переместительное и сочетательное свойства умножения позволяют сформулировать правило преобразования произведений.
При умножении нескольких чисел, их можно как угодно переставлять и объединять в группы.
Свойство нуля при умножении
Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.
Распределительное свойство умножения относительно сложения
Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить полученные результаты.
Это свойство справедливо для любого количества слагаемых.
Распределительное свойство умножения относительно вычитания
Чтобы умножить разность на число, можно умножить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе.
В буквенном виде свойство записывается так:
Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
Свойства деления
Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.
, где « k » — любое натуральное число.
Обратите внимание, что именно свойство деления выше позволяет нам сокращать дроби.
Использование всех рассмотренных выше свойств позволяет нам выполнять упрощение выражений.
Общие сведения
В математике любое действие принято называть операцией. Согласно математическому определению под ней понимают представления соответствия одному или нескольких элементам аргумента иного элемента. Все операции разделяют на арифметические и гипероперации. К первым относят сложение и вычитание. Вторые же включают в себя:
При умножении участвуют два члена (аргумента). Один из них называют множителем, а другой сомножителем. Но вместе с тем в учебниках используют и другие названия — множимое и множитель. Результатом умножения является не что иное, как произведение. Так как перемножение по своей сути является коммутативной операцией, то есть характеризуется свойством переместительности, порядок записи членов не оказывает влияния на результат.
Наряду с таблицей существуют и законы умножения. В 5 классе среднеобразовательной школы учащиеся проходят эти свойства, закладывая фундамент для освоения быстрого счёта. По своей сути произведение является результатом сложения одного из чисел столько раз, сколько указывает второе. Например, пусть имеется девять рядов. В каждом из них лежит пятнадцать яблок. Чтобы вычислить, сколько же всего фруктов необходимо, нужно сложить число пятнадцать само с собой девять раз. В ответе и получится искомое количество.
Эта неудобная операция сложения заменяется умножением. Другими словами, нужно просто число рядов умножить на количество яблок в каждом из них: k = 15 * 9 = 135 штук. При этом, согласно свойству умножения, порядок перемножения не имеет значения, так k = 9 * 15 = 135 штук.
Под умножением двух натуральных чисел понимают действие, результат которого равен сумме одинаковых слагаемых, определяемой первым из умножаемых чисел. При этом второе из этих чисел указывает количество слагаемых. В этом и заключена суть умножения двух натуральных чисел. Можно сформулировать простое определение действию: под произведением понимают результат, полученный суммированием слагаемого, при этом одно из перемножаемых чисел указывает на количество слагаемых.
Свойства произведения
Изучение математиками процесса умножения позволило им обнаружить ряд закономерностей, характерных для этого действия. Их назвали свойствами умножения. Наиболее часто при решении задач, при котором используется нахождение произведения, используют шесть законов умножения:
Сочетательный и переместительный законы были получены путём изучения результатов действия сложения. Они довольно похожи между собой. При сложении используется два правила: от перемены мест слагаемых результат остаётся неизменным, и при сложении нескольких членов можно сложить только два из них, а после полученную сумму прибавить к оставшимся. Именно на этих свойствах и построены два закона умножения. Сочетательное свойство сложения и умножения вместе с переместительным законом используют для существенного ускорения расчётов.
Например, пусть необходимо вычислить выражение: 15 * 3 * 4 * 5 + 1 * 2 * 3 * 4 * 5 * 6. Пример состоит из двух слагаемых. Первое, используя сочетательный закон, можно упростить. То есть не выполнять перемножение последовательно, что трудно сделать в уме, а вначале умножить первый и второй член, а затем третий с четвёртым, а уже после полученные произведения перемножить между собой: (15 * 3) * (4 * 5) = 45 * 20 = 900. Второе же слагаемое проще вычислить последовательно. В итоге получится: 900 + 720 = 1620.
Формулировка и объяснение
Сочетательный закон, а его часто называют ассоциативным, гласит, что при умножении любого количества множителей результат не поменяется, если группу этих множителей подменить произведением. Математической формулой это утверждение можно записать в виде: a * b * c = (a * b) * c = a * (b * c).
Для понимания этого действия нужно представить прямоугольник со сторонами три и пять сантиметров, нарисованный на тетрадном листе в клетку. Фигуру можно разбить на одинаковые единичные (сантиметровые) квадраты, а после подсчитать их количество. Сделать это можно несколькими способами.
Например, зная, что общее количество квадратов будет равняться произведению пяти на три, а каждый квадрат образуется четырьмя клетками, общее число будет равняться n = (5 * 3) *4 = 60 штук. Другой способ можно построить на том, что в каждом столбце находится три квадрата. Отсюда следует, что столбец содержит 3 * 4 клетки. Общее число клеток будет равняться: 5 * (3 * 4) = 60 штук.
Получается, что два способа равноправны, то есть (5 * 3) * 4 = 5 * (3 * 4). Таким образом, если заменить члены буквенным обозначением, то получится сочетательное свойство умножения. Отсюда следует ещё одно правило. Оно позволяет не только менять местами множители, но и вносить их под знак скобки, тем самым определяя порядок решения.
Распределительное свойство удобно применять и относительно сложения и вычитания. Пусть имеется отрезок разделяющий прямоугольник. Количество единичных квадратов, с одной стороны, будет равняться произведению трёх умноженному на три, а с другой — трёх на два. В итоге получится: 3 * 3 + 3 * 2 = 15 штук. Иначе можно утверждать, что в каждой строчке фигуры размещены 3 + 2 квадрата. Исходя из этого, верно будет записать: 3 * (3 + 2) = 15 штук. Равенство 3 * 3 + 3 * 2 = 3 * (3+ 2) и есть распределительное свойство, довольно плотно использующееся с сочетательным законом.
Например, нужно найти результат действия 25 *1349 * 4. Используя переместительное и сочетательное свойство, удобно выполнить перестановку членов, благодаря чему можно найти ответ. Так, удобно объединить члены выражения следующим образом: 25 * 1349 * 4 = 1349* (25 * 4) = 1349 * 100 = 134900. Аналогичным образом можно поступить и при присутствии в задании знака сложения или вычитания. Например, 311 * 734 + 329 * 266 = 311 * (734 + 266) = 311 * 1000 = 311 000.
Решение примеров
Необходимо не только понять сочетательный закон, но и уметь применять его в практических заданиях. Тем более что решение примеров позволит закрепить теоретический материал и довести действия до автоматизма. Получив опыт группирования членов, можно будет, затрачивая минимальные усилия, перемножить любой сложности выражения. При этом некоторые действия даже выполнить в уме.
Существует несколько условий применения сочетательного свойства: в задании не может быть менее трёх числовых значений; выражение должно содержать только все знаки сложения или умножения. Например, для следующих выражений: 6 * 55 — 3, 6 * 34, 4 * 9 *12, 34:5 * 8, 4 *9 *234, закон применим только ко второму и последнему.
Вот ряд примеров, предназначенных для самостоятельного решения:
Следует отметить, что для освоения сочетательного свойства обычно хватает самостоятельно решить около двадцати различных примеров. При этом для проверки результата можно использовать обычный калькулятор или даже онлайн-калькуляторы.
Основные свойства сложения и умножения
п.1. Основные законы сложения и умножения
1. Переместительный закон
Сумма не меняется от перестановки её слагаемых: a + b = b + a.
2. Сочетательный закон
Сумма не зависит от группировки её слагаемых: (a + b) + c = a + (b + c) = a + b + c
Сумма нуля и любого числа равна этому числу: 0 + a = a
4. Свойство противоположных чисел
Сумма противоположных чисел равна нулю: a + (-a)=0
1. Переместительный закон
Произведение не меняется от перестановки его сомножителей: ab = ba.
2. Сочетательный закон
Произведение не зависит от группировки его сомножителей: (ab)c = a(bc) = abc
3. Распределительный закон
4. Свойство единицы
6. Свойство обратных чисел
Применение переместительных и сочетательных законов сложения и умножения к числовым выражениям значительно облегчает вычисления.
Пример 1. Найдите значение выражения, выбирая удобный порядок вычислений
$(3\frac <17> <25>+ 4\frac <7><9>) + (2\frac <8> <25>— 1\frac <4><9>) + \frac 23 \cdot 0,2 \cdot 0,8 \cdot 5 \cdot 1,25 =$
$= (3\frac <17> <25>+ 2\frac <8><25>) + (4\frac <7> <9>— 1\frac <4><9>) + \frac 23 \cdot (0,2 \cdot 0,5) \cdot (0,8 \cdot 1,25) =$
Пример 2. Вычислите удобным способом:
п.2. Приведение подобных слагаемых
Применение законов сложения и умножения к выражениям с переменными также даёт возможность их упростить, прежде всего, с помощью приведения подобных слагаемых.
Подобные слагаемые – это слагаемые в выражении с переменными, имеющие одинаковую буквенную часть (любое буквенное выражение); числа без буквенной части также считаются подобными слагаемыми.
Заметим, что в выражении 3ab+2ba слагаемые подобны, т.к. 2ba=2ab по переместительному закону умножения.
Получаем следующий алгоритм.
Алгоритм приведения подобных слагаемых
1. Провести перестановку слагаемых так, чтобы подобные слагаемые оказались рядом, сгруппировать их с помощью скобок.
2. Вынести за скобки буквенную часть подобных слагаемых.
3. Вычислить значение числового выражения в скобках. Это – новый числовой коэффициент.
4. Заменить подобные слагаемые в выражении полученным результатом.
Пример 3. Упростите выражение:
Пример 4. Упростите выражение и найдите его числовое значение, если x=8:
Законы математики
В нашей жизни есть законы, которые надо соблюдать. Соблюдение законов гарантирует стабильность и гармоничное развитие. Несоблюдение же законов приводит к печальным последствиям.
У математики есть свои законы, которые тоже следует соблюдать. Несоблюдение законов математики приводит в лучшем случае к тому, что оценка учащегося снижается, а в худшем случае приводит к тому, что падают самолёты, зависают компьютеры, улетают крыши домов от сильного ветра, снижается качество связи и тому подобные нехорошие явления.
Законы математики состоят из простых свойств. Эти свойства нам знакомы со школы. Но не мешает вспомнить их ещё раз, а лучше всего записать или выучить наизусть.
В данном уроке мы рассмотрим лишь малую часть законов математики. Их нам будет достаточно для дальнейшего изучения математики.
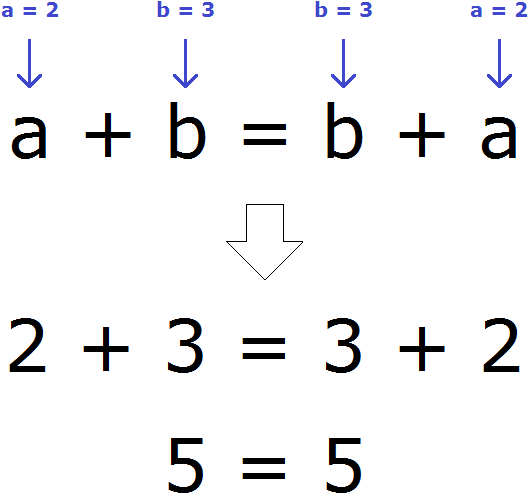
Переместительный закон сложения
Переместительный закон сложения говорит о том, что от перестановки мест слагаемых сумма не изменяется. Действительно, прибавьте пятерку к двойке — получите семёрку. И наоборот, прибавьте двойку к пятерке — опять получите семёрку:
Если положить на одну чашу весов 10 килограмм яблок и на другую чашу так же положить 10 килограмм яблок, то весы выровнятся, и не важно, что яблоки в пакетах лежат вразброс. Если мы возьмём пакет с весов и перемешаем яблоки находящиеся в нём, словно шары в лотерейном мешке, пакет всё так же будет весить 10 килограмм. От перестановки мест слагаемых сумма не изменится. Слагаемые в данном случае это яблоки, а сумма это итоговый вес.
Таким образом, между выражениями 5 + 2 и 2 + 5 можно поставить знак равенства. Это будет означать, что их сумма равна:
Полагаем что, вы изучили один из предыдущих уроков, который назывался выражения, поэтому мы без тени смущения запишем переместительный закон сложения с помощью переменных:
Сочетательный закон сложения
Сочетательный закон сложения говорит о том, что результат сложения нескольких слагаемых не зависит от порядка действий. Этот закон позволяет группировать слагаемые для удобства их вычислений.
Рассмотрим сумму из трёх слагаемых:
Чтобы вычислить данное выражение, можно сначала сложить числа 2 и 3 и полученный результат сложить с числом 5. Для удобства сумму чисел 2 и 3 можно заключить в скобки, указывая тем самым, что эта сумма будет вычислена в первую очередь:
2 + 3 + 5 = (2 + 3) + 5 = 5 + 5 = 10
Либо можно сложить числа 3 и 5, затем полученный результат сложить с числом 2
2 + 3 + 5 = 2 + (3 + 5) = 2 + 8 = 10
Видно, что в обоих случаях получается один и тот же результат.
Таким образом, между выражениями (2 + 3) + 5 и 2 + (3 + 5) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(2 + 3) + 5 = 2 + (3 + 5)
Запишем сочетательный закон сложения с помощью переменных:
Переместительный закон умножения
Переместительный закон умножения говорит о том, что если множимое и множитель поменять местами, то произведение не изменится. Давайте проверим так ли это. Умножим пятерку на двойку, а затем наоборот двойку на пятерку.
В обоих случаях получается один и тот же результат, поэтому между выражениями 5 × 2 и 2 × 5 можно поставить знак равенства, поскольку они равны одному и тому же значению:
5 × 2 = 2 × 5
Запишем переместительный закон умножения с помощью переменных:
Сочетательный закон умножения
Сочетательный закон умножения говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
Рассмотрим следующее выражение:
Данное выражение можно вычислять в любом порядке. Сначала можно перемножить числа 2 и 3, и полученный результат умножить на 4:
Либо сначала можно перемножить числа 3 и 4, и полученный результат перемножить с числом 2
Таким образом, между выражениями (2 × 3) × 4 и 2 × (3 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
Запишем сочетательный закон умножения с помощью переменных:
a × b × с = (a × b) × с = a × (b × с)
Пример 2. Найти значение выражения 1 × 2 × 3 × 4
Данное выражение можно вычислять в любом порядке. Вычислим его слева направо в порядке следования действий:
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число или число на сумму.
Рассмотрим следующее выражение:
Мы знаем, что сначала надо выполнить действие в скобках. Выполняем:
В главном выражении (3 + 5) × 2 выражение в скобках заменим на полученную восьмёрку:
8 × 2 = 16
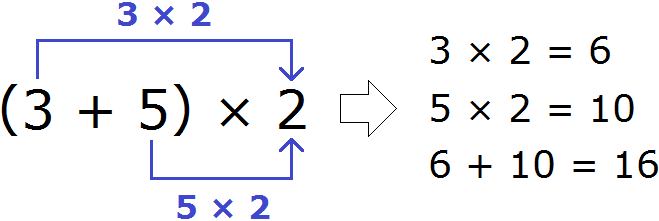
Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое, которое в скобках, нужно умножить на 2, затем сложить полученные результаты:
Мы рассмотрели распределительный закон умножения слишком развёрнуто и подробно. В школе этот пример записали бы очень коротко. К такой записи тоже надо привыкать. Выглядит она следующим образом:
(3 + 5) × 2 = 3 × 2 + 5 × 2 = 6 + 10 = 16
(3 + 5) × 2 = 6 + 10 = 16
Теперь запишем распределительный закон умножения с помощью переменных:
(a + b) × c = a × c + b × c
Давайте внимательно посмотрим на начало этого распределительного закона умножения. Начало у него выглядит так: (a + b) × c.
Если рассматривать выражение в скобках (a + b), как единое целое, то это будет множимое, а переменная с будет множителем, поскольку соединены они знаком умножения ×
Из переместительного закона умножения мы узнали, что если множимое и множитель поменять местами, то произведение не изменится.
c × (a + b) = c × a + c × b
Пример 2. Найти значение выражения 5 × (3 + 2)
Умножим число 5 на каждое слагаемое в скобках и полученные результаты сложим:
5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25
Пример 3. Найти значение выражения 6 × (5 + 2)
Умножим число 6 на каждое слагаемое в скобках и полученные результаты сложим:
6 × (5 + 2) = 6 × 5 + 6 × 2 = 30 + 12 = 42
Если в скобках располагается не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. Затем из полученного первого числа вычесть второе число. В принципе, ничего нового.
Пример 4. Найти значение выражения 5 × (6 − 2)
Умножим 5 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
5 × (6 − 2) = 5 × 6 − 5 × 2 = 30 − 10 = 20
Пример 5. Найти значение выражения 7 × (3 − 2)
Умножим 7 на каждое число в скобках. Затем из полученного первого числа вычтем второе число: