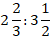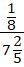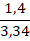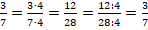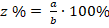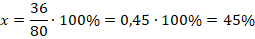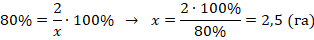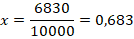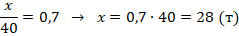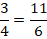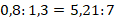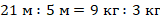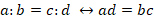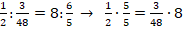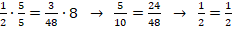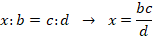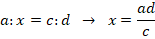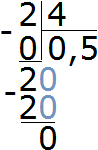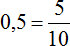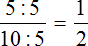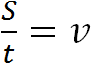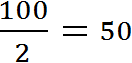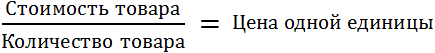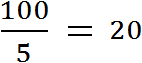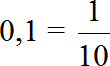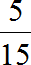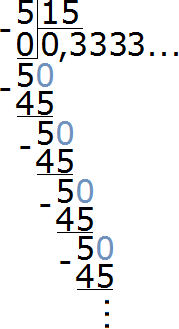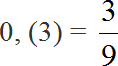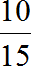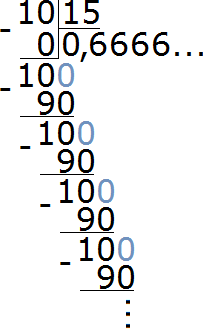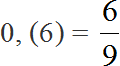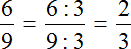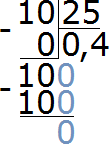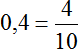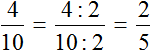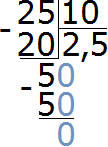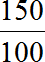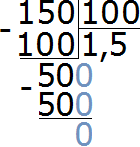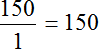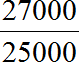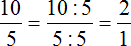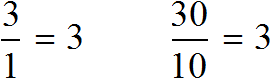Что такое соотношение между числами

Как рассчитать соотношение между двумя числами?

Чтобы рассчитать соотношение суммы, мы разделить сумму на общее количество частей в соотношении, а затем умножьте этот ответ на исходное соотношение.

В связи с этим, как вы решаете вопросы о соотношении?

к решить это вопрос, вы должны сначала сложить две половинки соотношение т.е. 4 + 2 = 6. Затем вам нужно разделить общую сумму, используя это число, например, 600/6 = 100. Чтобы вычислить, сколько получает каждый человек, вы затем умножаете его долю на 100.

В связи с этим, какое отношение 2 к 4?

Кроме того, как упростить соотношение?

Отношения можно полностью упростить, как и дроби. Чтобы упростить соотношение, разделите все числа в соотношении на одно и то же, пока они не перестанут делиться.

Как рассчитать коэффициент в процентах? Отношения часто выражаются в виде m: n или m / n. Чтобы преобразовать соотношение в процентную форму, просто разделите m на n, а затем умножьте результат на 100.

Как объяснить пропорции и пропорции?

Что такое метод отношения?

Оценка соотношения использует известные итоговые данные по совокупности для переменных, чтобы улучшить взвешивание от выборочные значения для оценки совокупности. Он сравнивает выборочную оценку переменной с генеральной совокупностью. … Этот метод применяет коэффициент выборки ко всей генеральной совокупности.

Какие есть примеры пропорций?

Если два соотношения эквивалентны друг другу, то говорят, что они пропорциональны. Например, соотношения 1: 2, 2: 4 и 3: 6 являются эквивалентными соотношениями.

Какое соотношение 3 к 5?

Отношение 3 к 5 просто означает, что на каждые 3 чего-то приходится 5 чего-то другогоВсего 8.

Чему эквивалентно соотношение 8 к 2?

С 8 до 2 можно уменьшить в 4, поэтому, чтобы иметь эквивалентное отношение, его также необходимо уменьшить до 4. Пример может включать от 16 до 4.

Какое соотношение 12 к 15?

Что такое простое соотношение?

Определение. Соотношение в простейшей форме, когда обе стороны являются целыми числами и нет целого числа, которое можно было бы разделить на обе стороны. Рассмотрим соотношение целых чисел, например, 6: 4. Его можно записать в виде дроби 64.

Что означает упрощение соотношения?

Что такое процентная формула?

Процент можно рассчитать, разделив значение на общее значение, а затем умножив результат на 100. Формула, используемая для расчета процента: (значение / общее значение) × 100%.

Что такое соотношение 70%?

Сколько 70 из 100 записано в процентах? Перевести дробь (соотношение) 70/100 Ответ: 70%

Каков процент соотношения 2 к 1?

Простое преобразование процентов и соотношений.

Что такое соотношение простыми словами?

Проще говоря, соотношение равно число, которое можно использовать для выражения одной величины как доли других. Два числа в соотношении можно сравнивать только в том случае, если они имеют одинаковую единицу измерения. Мы используем отношения для сравнения двух вещей.

Какая формула пропорции?

Формула процентной доли: Частей / целого = процентов / 100. Эту формулу можно использовать для определения процента заданного отношения и для нахождения недостающего значения части или целого.

Что такое метод цепного отношения?

метод расчета общего рыночного спроса на продукт, в котором базовое число, такое как общая численность населения страны, умножается на несколько процентов, например, численность населения выше и младше определенного возраста, численность населения, интересующегося автоспортом, численность населения…

Что такое метод оценки отношения?

Какая формула пропорции?

Для чего нужны пропорции?

Если вам известно одно соотношение в пропорции, вы можете использовать эту информацию, чтобы найти значения в другом эквивалентном соотношении. Использование пропорций может помочь вам решить такие проблемы, как увеличение рецепта, чтобы накормить большую толпу людей, создание дизайна с определенными согласованными функциями или увеличение или уменьшение изображения в масштабе.

Какое соотношение 12 к 5?

Перевести дробь (соотношение) 12/5 Ответ: 240%

Какой процент составляет соотношение 2 к 1?

Простое преобразование процентов и соотношений.

Какое соотношение 15 к 50?

Перевести дробь (соотношение) 15/50 Ответ: 30%

Источник

Что такое формула соотношения?

Когда мы сравниваем отношения между двумя числами, имеющими отношение к виду, мы используем формулу отношения. это обозначается как разделение числа двоеточием (:). Например, мы делаем торт, тогда в рецепте иногда говорится, что муку нужно смешать с водой в соотношении 2 части 1.…

Впоследствии, какое соотношение 3 к 5?

Отношение 3 к 5 просто означает, что на каждые 3 чего-то приходится 5 чего-то другогоВсего 8.

Кроме того, каков пример соотношения?

В математике соотношение указывает, сколько раз одно число содержит другое. Например, если в миске с фруктами находится восемь апельсинов и шесть лимонов, то соотношение апельсинов и лимонов будет восемь к шести (то есть 8∶6, что эквивалентно соотношению 4∶3).

Во-вторых, что такое соотношение? В математике соотношение сравнение двух или более чисел, указывающее их размеры по отношению друг к другу. Соотношение сравнивает две величины путем деления, при этом делимое или число, которое делится, называется антецедентом, а делитель или число, которое делит, называется следствием.

Как решить проблему соотношения?

Чтобы использовать пропорции для решения задач соотношения слов, нам нужно выполнить следующие шаги:

Как решить пример с соотношением?

Чтобы решить этот вопрос, вы должны сначала сложить две половины отношения, т.е. 4 + 2 = 6. Затем вам нужно разделить общую сумму, используя это число, например, 600/6 = 100. Чтобы определить, сколько получает каждый человек, затем вы умножаете их долю на 100.

Что означает соотношение 3 к 1?

Соотношение 3:1 означает что всего 4 части. Следовательно, дроби из отношения могут быть выведены как. 34 и 14. Они представляют собой проценты: 75%: 25%

Какие бывают 3 типа соотношений?

К трем основным категориям соотношений относятся: показатели рентабельности, левериджа и ликвидности. Знание индивидуальных коэффициентов в каждой категории и роли, которую они планируют, может помочь вам принять выгодные финансовые решения, касающиеся вашего будущего.

Как найти соотношение двух чисел?

Как вы читаете соотношение?

Чаще всего соотношение записывается в виде дроби, 3/6. Мы также могли бы написать это, используя слово «до», как «от 3 до 6». Наконец, мы могли бы записать это соотношение, используя двоеточие между двумя числами, 3: 6. Убедитесь, что вы понимаете, что это все способы написать одно и то же число.

Что такое соотношение простыми словами?

Проще говоря, соотношение равно число, которое можно использовать для выражения одной величины как доли других. Два числа в соотношении можно сравнивать, только если они имеют одинаковую единицу измерения.

Что такое простое определение соотношения?

1а: указанное частное двух математических выражений. b: соотношение количества, количества или размера между двумя или более вещами: пропорция. 2: выражение относительной стоимости золота и серебра в соответствии с валютным законодательством страны.

Как быстро рассчитать коэффициенты?

Как упростить соотношение?

коэффициенты может быть полностью упрощенный точно так же, как дроби. К упростить a соотношение, разделите все числа в соотношение на одно и то же число до тех пор, пока их больше нельзя будет разделить.

Как вы читаете соотношение?

В математике соотношение указывает, сколько раз одно число содержит другое. Например, если в миске с фруктами находится восемь апельсинов и шесть лимонов, то соотношение апельсинов и лимонов будет восемь к шести (то есть 8∶6, что эквивалентно соотношению 4∶3).

Как добавить коэффициент?

Уловка с добавлением соотношений заключается в том, чтобы следите за числом справа от двоеточия (:), это число называется знаменателем отношения. Когда знаменатели обоих соотношений одинаковы, сложить соотношение просто. Вы просто добавляете числа слева от двоеточия (это число называется числителем соотношений).

Как рассчитать коэффициент в процентах?

Отношения часто выражаются в виде m: n или m / n. Чтобы преобразовать соотношение в процентную форму, просто разделите m на n, а затем умножьте результат на 100.

Что такое 1/3 в процентах?

Какое соотношение 25?

Что означает соотношение 9 3 3 1?

Соотношение 9: 3: 3: 1 просто означает, что девять из них дикого типа, что означает, что они нормальные; шесть демонстрируют один мутантный и один нормальный признак, три нормальны для одного признака, остальные три нормальны для противоположного признака; один имеет оба мутантных фенотипа.

Какие бывают 5 типа соотношений?

Анализ коэффициентов состоит из расчета финансовых показателей с использованием пяти основных типов коэффициентов: прибыльность, ликвидность, активность, долг и рынок.

Каковы 4 финансовых коэффициента?

Финансовые коэффициенты обычно делятся на четыре категории:

Какие пять финансовых коэффициентов?

Какое соотношение 2 к 4?

Как найти соотношение двух чисел на калькуляторе?

Пример: упростить соотношение 6: 10

Как рассчитать соотношение между тремя числами?

Чтобы рассчитать соотношение трех чисел, мы выполняем 3 шага:

Источник

Отношение чисел

Отношения чисел: определение, свойства, виды

Определение

Отношением пары чисел называют результат их деления одно на другое. То есть понятия частного и отношения являются синонимами, обозначая одно и то же понятие. При этом число, которое делят, называют предыдущим членом, а число, на которое осуществляется деление, – последующим.

Для обозначения отношения чисел используется знак деления «:» либо черта дроби.

Общая форма записи отношения чисел: a : b или, соответственно, . В таких записях a – предыдущий член отношения, b – последующий. Обязательное условие для всякого отношения: .

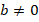
3:2

Здесь 3 и 4 – предыдущие члены отношений, 2 и 9 – последующие.

Свойства отношений

Свойство №1. Членами всякого отношения могут быть как целые, так и дробные, рациональные или другие числа.

Примеры отношений, члены которых являются целыми числами, приведены выше (см. Пример №1).

Пример №2. Отношения, члены которого дробные числа:

Свойство №2. Если члены отношения умножить (либо разделить) на одно и то же число, то его значение не изменится. Это свойство называют основным для отношений чисел.

Деление членов отношения на одно и то же число называют сокращением отношения.

Это свойство нередко используется для перехода от нецелых членов отношения к целым, что более удобно для расчетов.

Свойство №3. В отношении могут участвовать и более 2-х членов. Так, в прикладных задачах нередко используются пропорциональные величины, значения которых выражаются как раз через их отношения. Количество членов при этом может быть произвольным и равняться трем, четырем и так далее. В общем виде такие отношения записываются как a:b:c:d:…n и читаются так: «величины относятся между собой как a, b, c…»

Пример №4. Имеется треугольник, длины сторон которого относятся как 3:4:5.

Пример №5. Даны 4 пропорциональных числа, которые относятся между собой как 1:2:4:5.

В задачах, в которых приведены такого рода отношения, обычно вводится коэффициент пропорциональности и, используя свойства объекта, для которого они приведены, и (или) данные из условия, по заданному отношению находят абсолютные значения величин для этого объекта. При этом под абсолютными величинами понимают величины, выраженные в конкретных единицах измерения – кг, км и так далее.

Процентное отношение

Процентное отношение – это характерное и одно из наиболее распространенных направлений прикладного использования отношения чисел. Обозначение процентного отношения – % (процент). 1 % – это сотая часть от целого.

Процентное отношение основывается на обычном отношении, которое множат на 100. Процентное отношение показывает часть объекта (величины) в сравнении с его 100 частями, которые принимаются за целое.

Где a – часть целого, выраженная в единицах измерения, b – значение целого, выраженное в тех же единицах, z – количество процентов, которое составляет данная часть от целого.

Пример №6. На книжной полке 80 книг. Сколько процентов от этого количества составляют 36 книг?

Обозначим искомую величину через х. Тогда получаем:

Пример №7. Фермер посеял пшеницу на 2 га, что составляет 80 % от всех его посевных площадей. Какова общая посевная площадь, которой он располагает?

Обозначим искомую величину через х. Составим процентное отношение на основании данных задачи:

Нередко вместо понятия процентного отношения используют понятие долей. В этом случае целое абстрактно принимается за 1, а понятие процента не используется. Доля (часть) от данного целого в такой ситуации – это всегда будет величина, меньшая 1. Для определения доли (части) от целого используется обычное отношение:

Где b – часть от целого, c – величина целого, a – доля, которую b составляет от c.

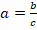
Специальной единицы измерения доля не имеет и измеряется просто в единицах.

Пример №8. Какую долю тиража изданной книги удалось продать писателю, если тираж составляет 10 тысяч экземпляров, а приобретено было 6830 книг?

Обозначим искомую величину через х. Составим отношение и найдем х:

Переход от долей к процентам предельно прост: достаточно умножить долю на 100. Так, в предыдущем примере 0,683 по отношению к общему тиражу составит .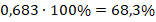

Пример №9. С 1 га планировалось собрать 40 тонн картофеля. Реальная урожайность составила 0,7 от планируемой. Сколько тонн картофеля собрали?

Обозначим искомую величину через х. Составим выражение для расчета реальной урожайности и найдем х:

Пропорция

Пропорцией называют равенство двух числовых отношений. В общем виде такое равенство записывают как 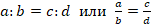, где a и d называют крайними членами пропорции, b и c – средними. Прочтение пропорции: отношение a к b равно отношению c к d, или a относится к b как c к d, или a во столько раз больше b во сколько больше d.

Пример №9. Примеры конкретных пропорций:

При решении практических задач с использованием отношений в виде пропорции чаще всего от деления переходят к умножению ее членов. Для этого используют основное ее свойство.

Основное свойство пропорции: произведение ее крайних членов равно произведению средних. Математически это свойство записывается так:

Если провести дальнейшие вычисления, то в итоге мы должны прийти к равенству чисел слева и справа. А именно:

Отсюда следует важная особенность: основное свойство применяют для проверки истинности составленной пропорции. Если в результате числовых преобразований получено верное равенство, то это означает, что исходные 4 числа действительно могут составить пропорцию.

Когда один из членов пропорции неизвестен и требуется найти его, то применяют правило: для вычисления неизвестного крайнего (среднего) члена перемножают средние (крайние) и делят полученное произведение на известный крайний (средний) член.

Математически это выражается так:

То есть для определения неизвестного члена перемножают пару соответствующих известных и делят их на тот известный член, который не имеет известной пары.

Источник

Что такое отношение двух чисел: определение, запись, примеры

В данной публикации мы рассмотрим, что такое отношение двух чисел, как записывается, а также, какие действия с ним можно выполнять, чтобы оно осталось неизменным. Представленная информация сопровождается практическими примерами.

Определение отношения чисел

Отношением двух чисел называется их частное, т.е. деление одного на другое.

Например, отношение 24 к 6 можно записать как или представить в виде обыкновенной дроби. В этом случае в знаменателе пишется число, с которым выполняется сравнение, а в числителе – то, которое сравнивается:

Примечание: вместо предлога “к” иногда используется “по сравнению с”.

С помощью отношения чисел показывается:

1. Во сколько раз одно из них больше другого (когда делимое больше делителя).

То есть 14 в два раза больше 7.

2. Какую часть одно число занимает в другом (делитель больше делимого).

То есть 5 составляет одну четвертую часть от числа 20 (или 25%).

Умножение/деление отношения на число

Если умножить или разделить оба элемента отношения на одно и то же число, отличное от нуля, в результате получится новое отношение, которое равно исходному.

Примечание: Это есть не что иное как основное свойство дроби.

Источник

Соотношения

Соотношением называют некоторую взаимосвязь между сущностями нашего мира. Это могут быть числа, физические величины, предметы, продукты, явления, действия и даже люди.

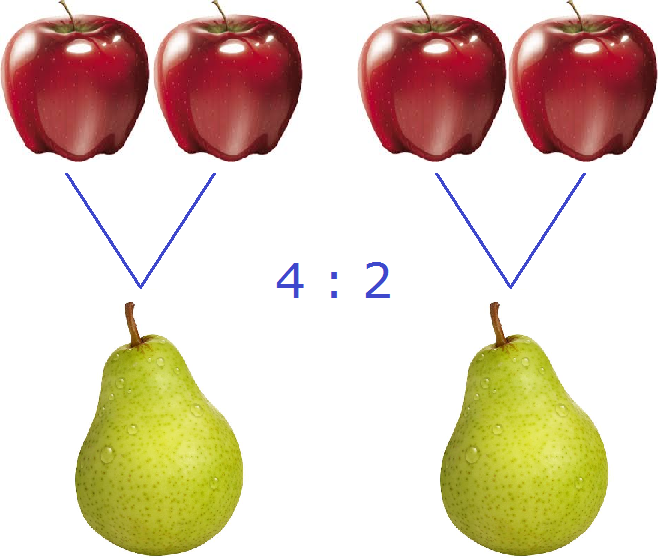
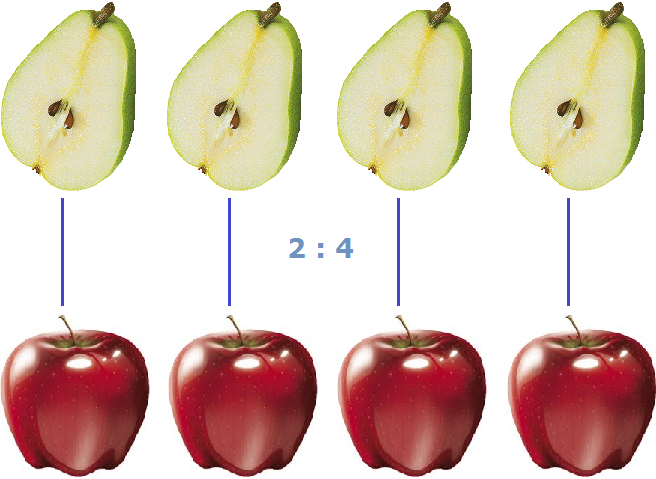
В повседневной жизни, когда речь заходит о соотношениях, мы говорим «соотношения того-то и того-то». Например, если в вазе лежит 4 яблока и 2 груши, то мы говорим «соотношения яблок и груш» или если поменять местами яблоки и груши, то «соотношения груш и яблок».

В математике соотношение чаще употребляется как «отношение того-то к тому-то». Например, соотношение четырёх яблок и двух груш, которые мы рассматривали выше, в математике будет читаться как «отношение четырех яблок к двум грушам» или если поменять местами яблоки и груши, то «отношение двух груш к четырем яблокам».

Запишем соотношение четырех яблок и двух груш с помощью символа соотношения:

Это соотношение можно прочитать как «четыре к двум» либо «соотношение четырех яблок и двух груш» либо «четыре яблока относится к двум грушам»

В дальнейшем соотношение мы будем называть просто отношением.

Что такое отношение?

Отношением в математике называют частное двух чисел.

Данное отношение представляет собой деление числа 4 на число 2. Если выполнить это деление, мы получим ответ на вопрос сколько яблок приходится на единицу груши

Получили 2. Значит четыре яблока и две груши (4 : 2) соотносятся (взаимосвязаны друг с другом) так, что на одну грушу приходится два яблока

На рисунке показано, как четыре яблока и две груши соотносятся между собой. Видно, что на каждую грушу приходятся два яблока.

Чтобы найти значение дроби нужно вспомнить, как делить меньшее число на большее

Получили 0,5. Переведём эту десятичную дробь в обыкновенную:

Сократим полученную обыкновенную дробь на 5

Получили ответ (половину груши). Значит две груши и четыре яблока (2 : 4) соотносятся (взаимосвязаны друг с другом) так, что на одно яблоко приходится половина груши

На рисунке показано, как две груши и четыре яблока соотносятся между собой. Видно, что на каждое яблоко приходится половинка груши.

Числа, из которых составлено отношение, называют членами отношения. Например, в отношении 4 : 2 членами являются числа 4 и 2.

Рассмотрим другие примеры соотношений. Для приготовления чего-либо составляется рецепт. Рецепт строят из соотношений между продуктами. Например, для приготовления овсяной каши обычно требуется стакан хлопьев на два стакана молока или воды. Получается соотношение 1 : 2 («один к двум» или «один стакан хлопьев на два стакана молока»).

Если перевернуть соотношение 1 : 2 то получится соотношение 2 : 1 («два к одному» или «два стакана молока на один стакан хлопьев»). Преобразуем соотношение 2 : 1 в дробь, получим . Вычислив эту дробь, получим 2. Значит два стакана молока и один стакан хлопьев соотносятся (взаимосвязаны друг с другом) так, что на один стакан хлопьев приходятся два стакана молока.

Пример 2. В классе 15 школьников. Из них 5 – это мальчики, 10 – девочки. Можно записать соотношение девочек и мальчиков 10 : 5 и преобразовать это соотношение в дробь . Вычислив эту дробь получим 2. То есть девочки и мальчики соотносятся между собой так, что на каждого мальчика приходятся две девочки

На рисунке показано, как десять девочек и пять мальчиков соотносятся между собой. Видно, что на каждого мальчика приходятся две девочки.

Соотношение не всегда можно обращать в дробь и находить частное. В некоторых случаях это будет нелогично.

Так, если перевернуть отношение получится , а это уже отношение мальчиков к девочкам. Если вычислить эту дробь получается 0,5. Получается, что пять мальчиков относятся к десяти девочкам так, что на каждую девочку приходится половина мальчика. Математически это конечно верно, но с точки зрения реальности не совсем разумно, ибо мальчик это живой человек и его нельзя просто так взять и разделить, как грушу или яблоко.

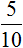
Умение построить правильное отношение — важный навык при решении задач. Так в физике, отношение пройденного расстояния ко времени есть скорость движения.

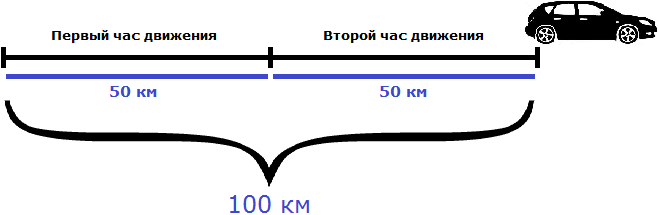
Предположим, что автомобиль проехал 100 километров за 2 часа. Тогда отношение пройденных ста километров к двум часам будет скоростью движения автомобиля:

Скоростью принято называть расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. А отношение, как было сказано ранее, позволяет узнать сколько количества одной сущности приходится на единицу другой. В нашем примере отношение ста километров к двум часам показывает сколько километров приходится на один час движения. Видим, что на каждый час движения приходятся 50 километров

Пример 2. Отношение стоимости товара к его количеству есть цена одной единицы товара

Если мы взяли в магазине 5 шоколадных батончиков и их общая стоимость составила 100 рублей, то мы можем определить цену одного батончика. Для этого нужно найти отношение ста рублей к количеству батончиков. Тогда получим, что на один батончик приходятся 20 рублей

Сравнение величин

Ранее мы узнали, что отношение между величинами разной природы образуют новую величину. Так, отношение пройденного расстояния ко времени есть скорость движения. Отношение стоимости товара к его количеству есть цена одной единицы товара.

Но отношение можно использовать и для сравнения величин. Результат выполнения такого отношения есть число, показывающее во сколько раз первая величина больше второй или какую часть первая величина составляет от второй.

Чтобы узнать во сколько раз первая величина больше второй, в числитель отношения нужно записать большую величину, а в знаменатель меньшую величину.

Чтобы узнать какую часть первая величина составляет от второй, в числитель отношения нужно записать меньшую величину, а в знаменатель большую величину.

Рассмотрим числа 20 и 2. Давайте узнаем во сколько раз число 20 больше числа 2. Для этого находим отношение числа 20 к числу 2. В числителе отношения записываем число 20, а в знаменателе — число 2

Значение данного отношения равно десяти

Отношение числа 20 к числу 2 есть число 10. Это число показывает во сколько раз число 20 больше числа 2. Значит число 20 больше числа 2 в десять раз.

Пример 2. В классе 15 школьников. 5 из них это мальчики, 10 – девочки. Определить во сколько раз девочек больше мальчиков.

Записываем отношение девочек к мальчикам. В числителе отношения записываем количество девочек, в знаменатель отношения — количество мальчиков:

Значение данного отношения равно 2. Значит в классе из 15 человек девочек в два раза больше мальчиков.

Здесь уже не стоит вопрос о том, сколько девочек приходятся на одного мальчика. В данном случае отношение используется для сравнения количества девочек с количеством мальчиков.

Пример 3. Какую часть число 2 составляет от числа 20.

Находим отношение числа 2 к числу 20. В числителе отношения записываем число 2, а в знаменателе — число 20

Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее

Значение отношения числа 2 к числу 20 есть число 0,1

В данном случае десятичную дробь 0,1 можно перевести в обыкновенную. Такой ответ будет проще для восприятия:

Значит число 2 от числа 20 составляет одну десятую часть.

Можно сделать проверку. Для этого найдём от числа 20. Если мы всё сделали правильно, то должны получить число 2

Получили число 2. Значит одна десятая часть от числа 20 есть число 2. Отсюда делаем вывод, что задача решена верно.

Пример 4. В классе 15 человек. 5 из них это мальчики, 10 – девочки. Определить какую часть от общего количества школьников составляют мальчики.

Записываем отношение мальчиков к общему количеству школьников. В числителе отношения записываем пять мальчиков, в знаменателе — общее количество школьников. Общее количество школьников это 5 мальчиков плюс 10 девочек, поэтому в знаменателе отношения записываем число 15

Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее. В данном случае число 5 нужно разделить на число 15

При делении 5 на 15 получается периодическая дробь. Переведём эту дробь в обыкновенную

Сократим полученную дробь на 3

Получили окончательный ответ . Значит мальчики составляют одну треть от всего класса

На рисунке видно, что в классе из 15 школьников треть класса составляют 5 мальчиков.

Если для проверки найти от 15 школьников, то мы получим 5 мальчиков

Записываем отношение числа 35 к числу 5. В числитель отношения нужно записать число 35, в знаменатель — число 5, но не наоборот

Значение данного отношения равно 7. Значит число 35 в семь раз больше числа 5.

Пример 6. В классе 15 человек. 5 из них это мальчики, 10 – девочки. Определить какую часть от общего количества составляют девочки.

Записываем отношение девочек к общему количеству школьников. В числителе отношения записываем десять девочек, в знаменателе — общее количество школьников. Общее количество школьников это 5 мальчиков плюс 10 девочек, поэтому в знаменателе отношения записываем число 15

Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее. В данном случае, число 10 нужно разделить на число 15

При делении 10 на 15 получается периодическая дробь. Переведём эту дробь в обыкновенную

Сократим полученную дробь на 3

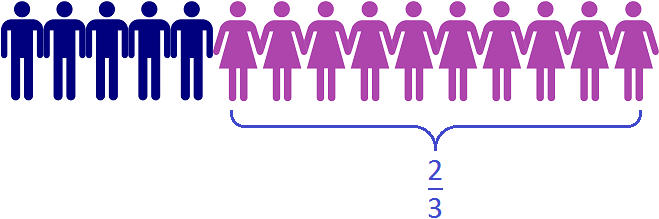
На рисунке видно, что в классе из 15 школьников две трети класса составляют 10 девочек.

Если для проверки найти от 15 школьников, то получим 10 девочек

Пример 7. Какую часть 10 см составляют от 25 см

Записываем отношение десяти сантиметров к двадцати пяти сантиметрам. В числителе отношения записываем 10 см, в знаменателе — 25 см

Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее. В данном случае число 10 нужно разделить на число 25

Переведём полученную десятичную дробь в обыкновенную

Сократим полученную дробь на 2

Получили окончательный ответ . Значит 10 см составляют от 25 см.

Пример 8. Во сколько раз 25 см больше 10 см

Записываем отношение двадцати пяти сантиметров к десяти сантиметрам. В числителе отношения записываем 25 см, в знаменателе — 10 см

Найдём значение данного отношения

Получили ответ 2,5. Значит 25 см больше 10 см в 2,5 раза (в два с половиной раза)

Важное замечание. При нахождении отношения одноименных физических величин эти величины обязательно должны быть выражены в одной единице измерения, в противном случае ответ будет неверным.

Например, если мы имеем дело с двумя длинами и хотим узнать во сколько раз первая длина больше второй или какую часть первая длина составляет от второй, то обе длины сначала нужно выразить в одной единице измерения.

Пример 9. Во сколько раз 150 см больше 1 метра?

Сначала сделаем так, чтобы обе длины были выражены в одной единице измерения. Для этого переведем 1 метр в сантиметры. Один метр это сто сантиметров

1 м = 100 см

Теперь находим отношение ста пятидесяти сантиметров к ста сантиметрам. В числителе отношения записываем 150 сантиметров, в знаменателе — 100 сантиметров

Найдём значение данного отношения

Получили ответ 1,5. Значит 150 см больше 100 см в 1,5 раза (в полтора раза).

А если бы не стали переводить метры в сантиметры и сразу попытались найти отношение 150 см к одному метру, то у нас получилось бы следующее:

Получилось бы, что 150 см больше одного метра в сто пятьдесят раз, а это неверно. Поэтому обязательно нужно обращать внимание на единицы измерения физических величин, которые участвуют в отношении. Если эти величины выражены в разных единицах измерения, то для нахождения отношения этих величин, нужно перейти к одной единице измерения.

Пример 10. В прошлом месяце зарплата человека составляла 25000 рублей, а в текущем месяце зарплата выросла до 27000 рублей. Определить во сколько раз выросла зарплата

Записываем отношение двадцати семи тысяч к двадцати пяти тысячам. В числителе отношения записываем 27000, в знаменателе — 25000

Найдём значение данного отношения

Получили ответ 1,08. Значит зарплата выросла в 1,08 раза. В будущем, когда мы познакомимся с процентами, такие показатели как зарплата будем выражать в процентах.

Пример 11. Ширина многоквартирного дома 80 метров, а высота 16 метров. Во сколько раз ширина дома больше его высоты?

Записываем отношение ширины дома к его высоте:

Значение данного отношения равно 5. Значит ширина дома в пять раз больше его высоты.

Свойство отношения

Отношение не изменится если его члены умножить или разделить на одно и тоже число.

Это одно из важнейших свойств отношения следует из свойства частного. Мы знаем, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится. А поскольку отношение является ничем иным как делением, то свойство частного работает и для него.

В нашем примере удобнее разделить члены отношения на их наибольший общий делитель (НОД).

НОД членов 10 и 5 это число 5. Поэтому можно разделить члены отношения на число 5

Получили новое отношение . Это есть отношение два к одному (2:1). Данное отношение, как и прошлое отношение 10:5 показывает, что на одного мальчика приходятся две девочки.

На рисунке показано отношение 2 : 1 (два к одному). Как и в прошлом отношении 10 : 5 на одного мальчика приходятся две девочки. Другими словами, отношение не изменилось.

Пример 2. В одном классе 10 девочек и 5 мальчиков. В другом классе 20 девочек и 10 мальчиков. Во сколько раз в первом классе девочек больше мальчиков? Во сколько раз во втором классе девочек больше мальчиков?

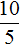
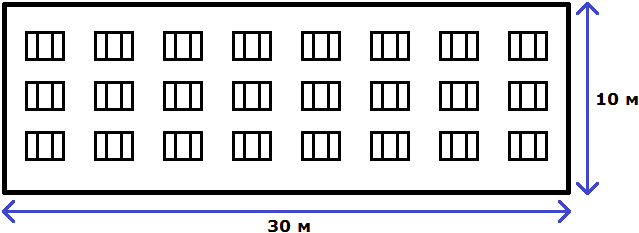
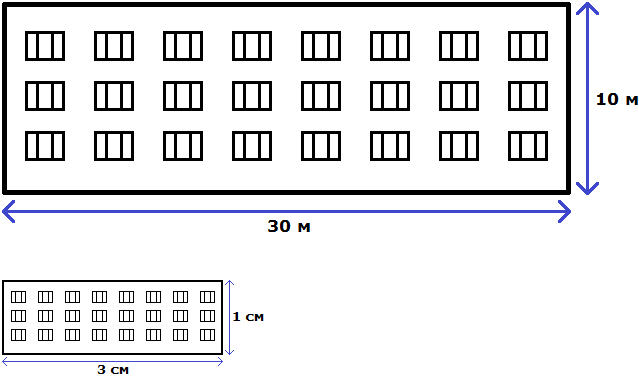
В обоих классах девочек в два раза больше мальчиков, поскольку отношения и равны одному и тому же числу.

Свойство отношения позволяет строить различные модели, которые имеют схожие параметры с реальным объектом. Предположим, что многоквартирный дом имеет ширину 30 метров и высоту 10 метров.

Переведем метры в сантиметры. 3 метра это 300 сантиметров, а 1 метр это 100 сантиметров

3 м = 300 см

1 м = 100 см

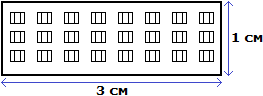
Имеем отношение 300 см : 100 см. Разделим члены этого отношения на 100. Получим отношение 3 см : 1 см. Теперь можно нарисовать дом с шириной 3 см и высотой 1 см

Конечно нарисованный дом намного меньше реального дома, но неизменным осталось отношение ширины и высоты. Это позволило нам нарисовать дом, максимально похожий на реальный

Отношение можно понимать и другим образом. Изначально было сказано, что у реального дома ширина составляет 30 метров, а высота 10 метров. Итого получается 30+10, то есть 40 метров.

Эти 40 метров можно понимать, как 40 частей. Отношение 30 : 10 говорит о том, что 30 частей приходится на ширину, а 10 частей на высоту.

Далее члены отношения 30 : 10 были разделены на 10. В результате получилось отношение 3 : 1. Это отношение можно понимать, как 4 части, три из которых приходится на ширину, одна — на высоту. В этом случае обычно требуется узнать сколько конкретно метров приходится на ширину и высоту.

Другими словами, нужно узнать сколько метров приходится на 3 части и сколько метров приходится на 1 часть. Сначала надо узнать сколько метров приходится на одну часть. Для этого общие 40 метров нужно разделить на 4, поскольку в отношении 3 : 1 всего четыре части

Далее с помощью умножения определяют сколько метров приходятся на ширину и высоту. Члены, которые даны в отношении используют в качестве сомножителя.

Определим сколько метров приходится на ширину:

Определим сколько метров приходится на высоту:

Несколько членов отношения

Если в отношении дано несколько членов, то их можно понимать как части от чего-либо.

Отношение 2 : 1 : 3 говорит о том, что мама получила 2 части, папа — 1 часть, дочка — 3 части. Другими словами, каждый член отношения 2 : 1 : 3 это определенная часть от 18 яблок:

Узнаем сколько яблок приходится на одну часть. Для этого 18 яблок разделим на 6

18 : 6 = 3 (яблока на одну часть)

Узнаем сколько яблок получила мама:

Узнаем сколько яблок получил папа:

Узнаем сколько яблок получила дочка:

4 килограмма нового серебра будет содержать 3 части никеля, 4 части цинка и 13 частей меди. Сначала узнаем сколько всего частей будет в четырех килограммах серебра:

3 + 4 + 13 = 20 (частей)

Определим сколько килограммов будет приходиться на одну часть:

Определим сколько килограммов никеля будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что три части сплава содержат никель. Поэтому умножаем 0,2 на 3:

0,2 кг × 3 = 0,6 кг никеля

Теперь определим сколько килограммов цинка будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что четыре части сплава содержат цинк. Поэтому умножаем 0,2 на 4:

0,2 кг × 4 = 0,8 кг цинка

Теперь определим сколько килограммов меди будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что тринадцать частей сплава содержат медь. Поэтому умножаем 0,2 на 13:

0,2 кг × 13 = 2,6 кг меди

Значит, чтобы получить 4 кг нового серебра, нужно взять 0,6 кг никеля, 0,8 кг цинка и 2,6 кг меди.

Определим сколько граммов сплава приходится на одну часть. В условии сказано, что для изготовления куска латуни требуется 120 г меди. Также сказано, что три части сплава содержат медь. Если разделить 120 на 3, мы узнаем сколько граммов сплава приходится на одну часть:

120 : 3 = 40 граммов на одну часть

Теперь определим сколько требуется цинка для изготовления куска латуни. Для этого 40 граммов умножим на 2, поскольку в отношении 3 : 2 указано, что две части содержат цинк:

40 г × 2 = 80 граммов цинка

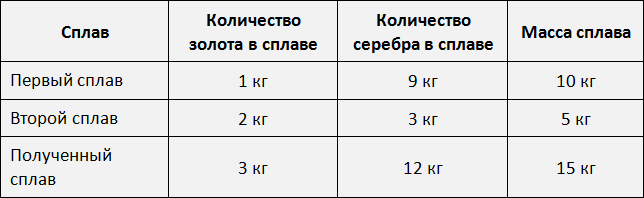
Пример 4. Взяли два сплава золота и серебра. В одном количество этих металлов находится в отношении 1 : 9, а в другом 2 : 3. Сколько нужно взять каждого сплава, чтобы получить 15 кг нового сплава, в котором золото и серебро относилось бы как 1 : 4?

Решение

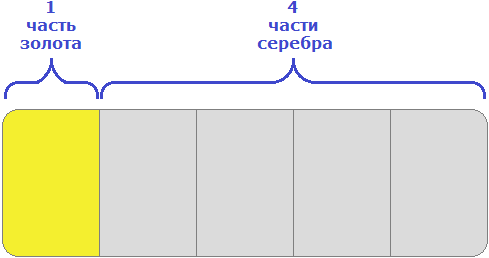
15 кг нового сплава должны состоять в отношении 1 : 4. Это отношение говорит о том, что на одну часть сплава будет приходиться золото, а на четыре части будет приходиться серебро. Всего же частей пять. Схематически это можно представить следующим образом

Определим массу одной части. Для этого сначала сложим все части (1 и 4), затем массу сплава разделим на количество этих частей

1 + 4 = 5
15 кг : 5 = 3 кг

Одна часть сплава будет иметь массу 3 кг. Тогда в 15 кг нового сплава будет содержáться 3 × 1 = 3 кг золота и серебра 3 × 4 = 12 кг серебра.

Поэтому для получения сплава массой 15 кг нам нужно 3 кг золота и 12 кг серебра.

Теперь ответим на вопрос задачи — « Сколько нужно взять каждого сплава? »

Первого сплава мы возьмем 10 кг, поскольку золото и серебро в нём находятся в отношении 1 : 9. То есть этот первый сплав даст нам 1 кг золота и 9 кг серебра.

Второго сплава мы возьмем 5 кг, поскольку золото и серебро находятся в нём в отношении 2 : 3. То есть этот второй сплав даст нам 2 кг золота и 3 кг серебра.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Источник