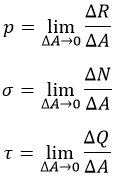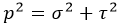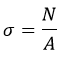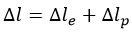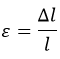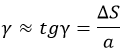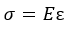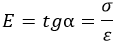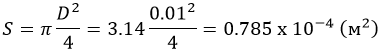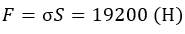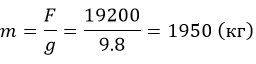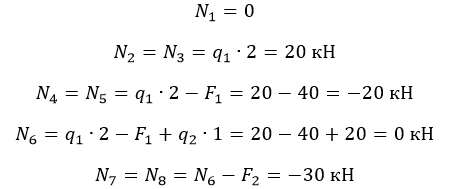Что такое сопромат определение
Сопротивление материалов
Сопротивление материалов (в обиходе — сопромат) — часть механики деформируемого твёрдого тела, которая рассматривает методы инженерных расчётов конструкций на прочность, жесткость и устойчивость при одновременном удовлетворении требований надежности, экономичности и долговечности. Сопротивление материалов относится к фундаментальным дисциплинам общеинженерной подготовки специалистов с высшим техническим образованием, за исключением специальностей, не связанных с проектированием объектов, для которых прочность является важным показателем.
Содержание
Определение
Сопротивление материалов базируется на понятии «прочность», что является способностью материала противостоять приложенным нагрузкам и воздействиям без разрушения. Сопротивление материалов оперирует такими понятиями как: внутренние усилия, напряжения, деформации. Приложенная внешняя нагрузка к некоторому телу порождает внутренние усилия в нём, противодействующие активному действию внешней нагрузки. Внутренние усилия, распределенные по сечениям тела называются напряжениями. Таким образом, внешняя нагрузка порождает внутреннюю реакцию материала, характеризующуюся напряжениями,которые в свою очередь прямо пропорциональны деформациям тела. Деформации бывают линейные такие как удлинение,укорочение, сдвиг и углы поворота сечений. Основные понятия сопротивления материалов оценивающие способность материала сопротивляться внешним воздействиям являются:
Связь с другими науками
В теоретической части сопротивление материалов базируется на математике и теоретической механике, в экспериментальной части — на физике и материаловедении и применяется при проектировании машин, приборов и конструкций. Практически все специальные дисциплины подготовки инженеров по разным специальностям содержат разделы курса сопротивления материалов, так как создание работоспособной новой техники невозможно без анализа и расчета её прочности, жёсткости и надёжности.
Задачей сопротивления материалов, как одного из разделов механики сплошной среды, является определение деформаций и напряжений в твёрдом упругом теле, которое подвергается силовому или тепловому воздействию.
Эта же задача среди других рассматривается в курсе теории упругости. Однако методы решения этой общей задачи в том и другом курсах существенно отличаются друг от друга. Сопротивление материалов решает её главным образом для бруса, базируясь на ряде гипотез геометрического или физического характера. Такой метод позволяет получить, хотя и не во всех случаях, вполне точные, но достаточно простые формулы для вычисления напряжений. Также поведением деформируемых твёрдых тел под нагрузкой занимается теория пластичности и теория вязкоупругости.
Гипотезы и допущения
Расчет конструкций и их элементов является или теоретически невозможным, или практически неприемлемым по своей сложности. Поэтому в сопротивлении материалов существует модель идеализированного деформируемого тела.
Эти положения ограниченно применимы к решению конкретных закдач. Например, для решения задач устойчивости утверждения 4-6 не справедливы, утверждение 3 справедливо не всегда.
Теории прочности
Прочность конструкций определяется с использованием теории разрушения — науки о прогнозировании условий, при которых твердые материалы разрушаются под действием внешних нагрузок. Материалы, как правило, подразделяются на разрушающиеся хрупко и пластично. В зависимости от условий (например, температура, состояние напряжений, виды нагрузки) большинство материалов может быть отнесено к хрупким или пластичным или обоим видам одновременно. Тем не менее, для большинства практических ситуаций, материалы могут быть классифицированы как хрупкие или пластичные. Несмотря на то, что теория разрушения находится в разработке уже более 200 лет, уровень её приемлемости для механики сплошных сред, не всегда достаточен.
В математических терминах, теория разрушения выражается в виде различных критериев разрушения, которые справедливы для конкретных материалов. Критерием разрушения является поверхность разрушения, выраженная через напряжения или деформации. Поверхность разрушения разделяет «поврежденное» и «не поврежденное» состояния. Для «поврежденного» состояния трудно дать точное физическое определение. Поэтому это понятие следует рассматривать как рабочее определение, используемое в инженерном сообществе. Термин «поверхность разрушения», используемый в теории прочности, не следует путать с аналогичным термином, который определяет физическую границу между поврежденными и не поврежденными частями тела. Довольно часто феноменологические критерии разрушения одного и того же вида используются для прогнозирования хрупкого и пластичного разрушения.
Среди феноменологических теорий прочности наиболее известными являются следующие теории, которые принято называть «классическими» теориями прочности:
1. Теория наибольших нормальных напряжений.
2. Теория наибольших деформаций.
3. Теория наибольших касательных напряжений Треска (Tresca).
4. Теория наибольшей удельной потенциальной энергии формоизменения фон Мизеса (von Mises).
Классические теории прочности имеют существенные ограничения для их применения. Так теории наибольших нормальных напряжений и наибольших деформаций применимы лишь для расчета прочности хрупких материалов, причём только для некоторых определённых условий нагружения. Поэтому эти теории прочности сегодня применяют весьма ограниченно. Из перечисленных теорий наиболее часто используют теорию Мора, которую также называют критерием Мора-Кулона. Кулон (Coulomb) в 1781 г. на основе выполненных им испытаний установил закон сухого трения, который использовал для расчета устойчивости подпорных стенок. Математическая формулировка закона Кулона совпадает с теорией Мора, если в ней выразить главные напряжения через касательные и нормальные напряжения на площадке среза. Достоинством теории Мора является то, что она применима к материалам, имеющим разные сопротивления сжатию и растяжению, а недостатком то, что она учитывает влияние только двух главных напряжений — максимального и минимального. Поэтому теория Мора не точно оценивает прочность при трехосном напряженном состоянии, когда необходимо учитывать все три главных напряжения. Кроме того, при использовании эта теория не учитывается поперечное расширение (дилатацию) материала при сдвиге. На эти недостатки теории Мора неоднократно обращал внимание А. А. Гвоздев, который доказал неприменимость теории Мора для бетона [2].
На смену «классическим» теориям прочности в современной практике пришли многочисленные новые новые теории разрушения. Большинство из них используют различные комбинации инвариантов тензора напряжений Коши (Cauchy) Среди них наиболее известны следующие критерии разрушения:
Перечисленные критерии прочности предназначены для расчета прочности однородных (гомогенных) материалов. Некоторые из них используются для расчёта анизотропных материалов.
Для расчета прочности неоднородных (не гомогенных) материалов используется два подхода, называемые макро-моделированием и микро-моделированием. Оба подхода ориентированы на использование метода конечных элементов и вычислительной техники. При макро-моделировании предварительно выполняется гомогенизация — условная замена неоднородного (гетерогенного) материала на однородный (гомогенный). При микро-моделировании компоненты материала рассматриваются с учётом их физических характеристик. Микро-моделирование используют в основном в исследовательских целях, так как расчет реальных конструкций требует чрезмерно больших затрат машинного времени. Методы гомогенизации широко используются для расчета прочности каменных конструкций, в первую очередь для расчета стен-диафрагм жесткости зданий. Критерии разрушения каменных конструкций учитывают многообразные формы разрушения каменной кладки. Поэтому поверхность разрушения, как правило. принимается в виде нескольких пересекающихся поверхностей, которые могут иметь разную геометрическую форму.
Применение
Методы сопротивления материалов широко используются при расчете несущих конструкций зданий и сооружений, в дисциплинах связанных с проектированием деталей машин и механизмов.
Как правило, именно из-за оценочного характера результатов, получаемых с помощью математических моделей этой дисциплины, при проектировании реальных конструкций все прочностные характеристики материалов и изделий выбираются с существенным запасом (в несколько раз относительно результата, полученного при расчетах).
В студенческой среде сопротивление материалов считается одной из наиболее сложных общепрофессиональных дисциплин, что дало богатую пищу студенческому фольклору и породило целый ряд шуток и анекдотов.
См. также
Литература
Основные понятия и определения сопромата.
Сопротивление материалов – раздел механики деформируемого твердого тела, в котором рассматриваются методы расчета элементов машин и сооружений на прочность, жесткость и устойчивость.
Прочностью называется способность материала сопротивляться воздействию внешних сил, не разрушаясь и без появления остаточных деформаций. Расчеты на прочность дают возможность определить размеры и форму деталей, выдерживающих заданную нагрузку, при наименьшей затрате материала.
Жесткостью называется способность тела сопротивляться образованию деформаций. Расчеты на жесткость гарантируют, что изменения формы и размеров тела не превзойдут допустимых норм.
Устойчивостью называется способность конструкций сопротивляться усилиям, стремящимся вывести их из состояния равновесия. Расчеты на устойчивость предотвращают внезапную потерю равновесия и искривление элементов конструкции.
Долговечность состоит в способности конструкции сохранять необходимые для эксплуатации служебные свойства в течение заранее предусмотренного срока времени.
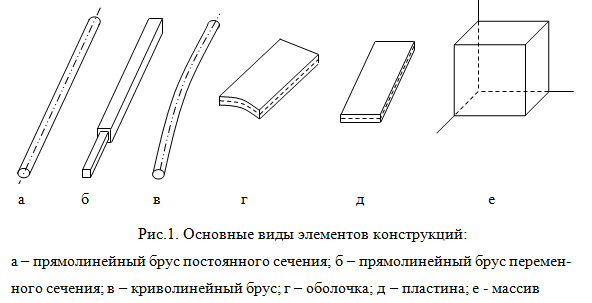
Оболочка (рис.1, г) это тело, один из размеров которого (толщина) намного меньше остальных. Если поверхность оболочки представляет собой плоскость, то объект называют пластиной (рис.1, д). Массивами называются тела, у которых все размеры одного порядка (рис.1, е). К ним относятся фундаменты сооружений, подпорные стены и др.
Эти элементы в сопротивлении материалов используются для составления расчетной схемы реального объекта и проведения ее инженерного анализа. Под расчетной схемой понимается некоторая идеализированная модель реальной конструкции, в которой отброшены все малосущественные факторы, влияющие на ее поведение под нагрузкой
Допущения о свойствах материала
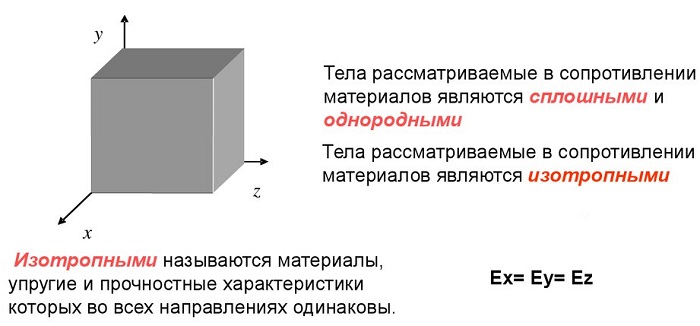
Материал считается сплошным, однородным, изотропным и идеально упругим.
Сплошность – материал считается непрерывным. Однородность –физические свойства материала одинаковы во всех его точках.
Изотропность – свойства материала одинаковы по всем направлениям.
Идеальная упругость – свойство материала ( тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.
Допущения о деформациях
1. Гипотеза об отсутствии первоначальных внутренних усилий.
2. Принцип неизменности начальных размеров – деформации малы по сравнению с первоначальными размерами тела.
3. Гипотеза о линейной деформируемости тел – деформации прямо пропорциональны приложенным силам (закон Гука).
4. Принцип независимости действия сил.
5. Гипотеза плоских сечений Бернулли – плоские поперечные сечения бруса до деформации остаются плоскими и нормальными к оси бруса после деформации.
6. Принцип Сен-Венана – напряженное состояние тела на достаточном удалении от области действия локальных нагрузок очень мало зависит от детального способа их приложения
Внешние силы
Внутренние силы. Метод сечений.
Действие на тело внешних сил приводит к его деформации (меняется взаимное расположение частиц тела). Вследствие этого между частицами возникают дополнительные силы взаимодействия. Это силы сопротивления изменению формы и размеров тела под действием нагрузки, называют внутренними силами (усилиями). С увеличением нагрузки внутренние усилия возрастают. Выход из строя элемента конструкции наступает при превышении внешних сил некоторого предельного для данной конструкции уровня внутренних усилий. Поэтому оценка прочности нагруженной конструкции требует знания величины и направления возникающих внутренних усилий. Значения и направления внутренних сил в нагруженном теле определяют при заданных внешних нагрузках методом сечений.
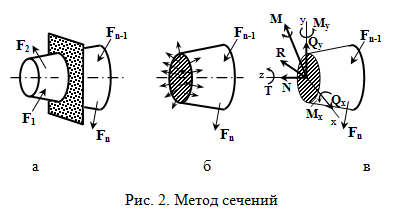
Метод сечений (см. рис. 2) состоит в том, что брус, находящийся в равновесии под действием системы внешних сил, мысленно рассекают на две части (рис. 2, а), и рассматривают равновесие одной из них, заменяя действие отброшенной части бруса системой внутренних сил, распределенных по сечению (рис. 2, б). Заметим, что внутренние силы для бруса в целом, становятся внешними для одной из его частей. Причем во всех случаях внутренние усилия уравновешивают внешние силы, действующие на отсеченную часть бруса.
Что такое сопромат
Сопромат занимается вопросами прочности, жесткости и устойчивости
Прочность это способность конструкции и ее элементов выдерживать нагрузку, к ней приложенную без разрушений в виде пластических деформаций или хрупких трещин
Жесткость это способность элементов конструкции получая деформации (изгиб, растяжение — сжатие и др.) не ревышать при этом допустимые значения
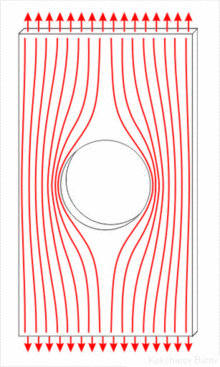
При продольном сжатии длинных и тонких стержней может появиться изгиб. Переход из прямолинейного состояния в изогнутое — есть потеря устойчивости.
Сопротивление материалов — это наука, которая занимается расчетом на прочность, жесткость и устойчивость.
Сопромат, сопротивление материалов что это?
Всего три вопроса, но вот разнообразие этих расчетов очень широкое. Сопромат занимается, например расчетами на прочность при следующих видах деформаций:
После проверки элемента конструкции на прочность нужно провести расчет на жесткость.
Что изучает сопротивление материалов — видео урок
Видео урок в котором объясняется что изучает сопротивление материалов и о чем предмет сопротивление материалов:
Расчет на прочность
При расчете на прочность мы даем ответ вопрос: выдержит ли, не разрушится ли (сломается) наша конструкция, тело, объект.

Как видно из рисунков пластичные материалы, такие как медь, сталь при потере прочности меняют свои размеры значительно и еще говорят «текут» (за пределом текучести).
Хрупкие материалы, когда нагрузка превышает допустимую разрушаются в виде трещин. Это и характеризует хрупкие материалы.
Подробнее о прочности можно посмотреть видео по разрушению стального образца
Испытания стали на разрыв. Определение предела текучести, предела пропорциональности, предела прочности, а также упругих и пластичных деформаций
Расчет на жесткость
Дает ответ на второй вопрос: не будет ли прогиб, растяжение-сжатие, или другой вид деформации слишком большим.
Конечно же не комфортно ходить по полу в доме, который прогибается под ногами. Или когда крыша над головой «висит». Это и есть не жесткая конструкция. Она прочная, выдерживает, не «ломается», но, при этом, не жесткая.
Итак расчет на жесткость проверяет существующее перемещение в конструкции (деформация изгиба, растяжения или сжатия, кручения и др) с допустимым изменением этой величины, например прогиба.
Если расчетная величина меньше допустимой — условие жесткости соблюдается.
Расчет на устойчивость
Расчет на устойчивость дает ответ на еще один вопрос. Часто, колонны, поддерживающие крыши, балконы и другие конструкции, бывают большой длины (высоты).
В механических конструкциях тоже встречаются различные стержни, которые тонкие и длинные. Так вот, это и есть гибкость, такое понятие, которое определяется двумя показателями — длинное и тонкое сечение.
Ну линейка, например (только длинная сантиметров на 100). Если к ней приложить нагрузку на сжатие, то увеличивая ее все больше и больше в определенный момент времени, она изогнется.
Это явление называют потеря устойчивости. Она еще не «сломалась» (т.е. условие прочности соблюдается), но уже не такая какой мы ее запроектировали в конструкции. А это и есть потеря устойчивости. Мы должны заранее предусмотреть и рассчитать.
Какие бывают виды деформации
В нашей жизни, в природе, в строительных конструкциях, машинах и механизмах внешние воздействия: ветер, собственный вес объекта, вес других предметов и объектов вызывают различные изменения, которые мы называем деформацией. А деформации, которые возникают, разделяют на соответствующие виды:
Есть и другие, но пока остановимся на том, что названо. Так вот определение изменения усилий, вызывающих эти деформации, построение графиков этих изменений — называют построением эпюр внутренних усилий. Об этом сняты видео в соответствующих разделах. Так например при изгибе строят эпюры изгибающих моментов M и поперечных сил Q. При растяжении сжатии — строят эпюры продольных сжимающих и растягивающих внутренних усилий N. Пример решения такой задачи, на построение эпюр приведен по ссылке выше. Ну и в задачах на кручение — строят эпюры крутящих моментов.
Многочисленные учебники «Cопромат для чайников» создают для развенчания мифа о непостижимой сложности дисциплины. Этой наукой пугают на первых курсах вузов. Для начала расшифруем грозный термин «сопротивление материалов».
На деле – проста и решение почти не выходит за рамки школьной задачи о растяжении и сжатии пружины. Другое дело – найти слабое звено конструкции и свести расчет к несложной постановке. Так что не стоит зевать на лекциях по основам механики. При подготовке к урокам можно пользоваться решениями онлайн, но на экзаменах помогут только свои знания.
Что такое сопромат
Это методика расчета деталей, конструкций на способность выдерживать нагрузки в требуемой степени. Или хотя бы для предсказания последствий. Не более, хотя почему-то относят руководство к наукам.
Этой «наукой» прекрасно владели древнегреческие и древнеримские инженеры, сооружавшие сложнейшие механизмы. Понятия не имея о структуре, уравнении состояния вещества и прочих теориях, египтяне строили исполинские плотины и пирамиды.
Основные задачи по сопротивлению материалов
Задача следует напрямую из определения. А вот каковы критерии упомянутого слова «выдерживать»? Неясно, что скрывается под «материалом» и как реальные вещи схематизировать.
Требования
Перечислены далеко не все, но для статики и базовой программы хватит:
Прочность – способность образца воспринимать внешние силы без разрушения. Слегка мнущаяся под весом оборудования подставка никого не интересует. Основную-то функцию она выполняет.
Жесткость – свойство воспринимать нагрузку без существенного нарушения геометрии. Гнущийся под силой резания инструмент даст дополнительную погрешность обработки. К ошибке приведет деформация станины агрегата.
Устойчивость – способность конструкции сохранять стабильность равновесия. Поясним на примере: стержень находится под грузом, будучи прямым – выдерживает, а чуть изогнется – характер напряжения изменится, груз рухнет.
Материал и силы
Как всякая методика, сопромат принимает массу упрощений и прямо неверных допущений:
материал однороден, среда сплошная. Внутренние особенности в расчет не берутся;
свойства не зависят от направления;
образец восстанавливает начальные параметры при снятии нагрузки;
поперечные сечения не меняются при деформации;
в удаленных от места нагрузки местах усилие распределяется равно по сечению;
результат воздействия нагрузок равен сумме последствий от каждой;
деформации не влияют на точки приложения сил;
отсутствуют изначальные внутренние напряжения.
Схемы
Служат для создания возможности расчета реальных конструкций:
тело – объект с практически одинаковыми «длина х ширина х высота»;
брус (балка, стержень, вал) – характеризуется значительной длиной.
На рисунке показаны опоры с воспринимаемыми реакциями (обозначены красным цветом):
Рис. 1. Опоры с воспринимаемыми реакциями:
в) жесткая заделка (защемление).
Силы в сопромате
Приложенные извне, уравновешиваются возникающими изнутри. Напомним, рассматривается статическая ситуация. Материал «сопротивляется».
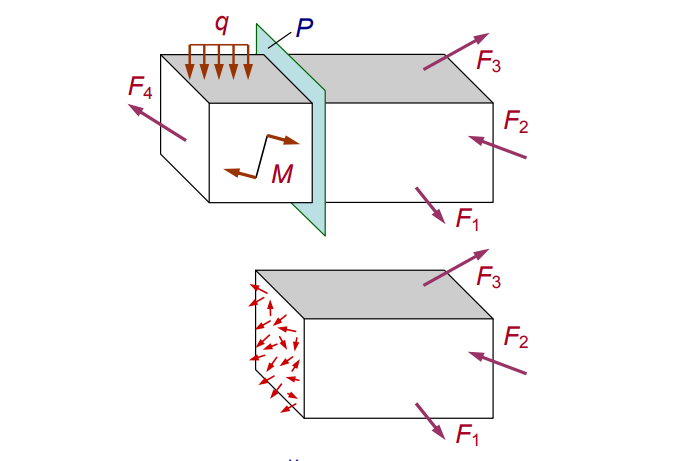
Разделим нагруженное тело виртуальным сечением P (см. рис. 2).
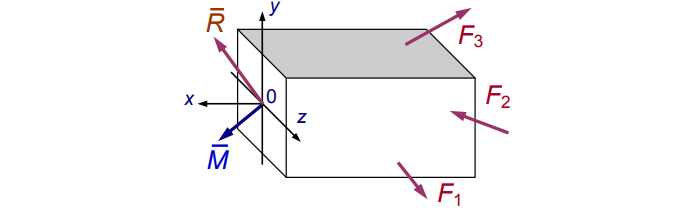
Заменим хаос равнодействующей R и моментом M (см. рис. 3):
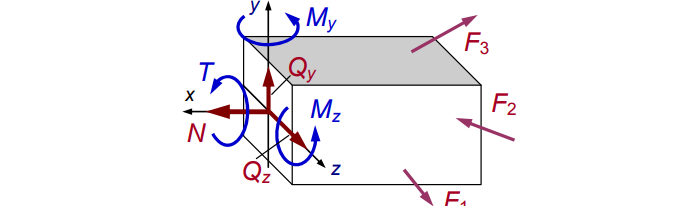
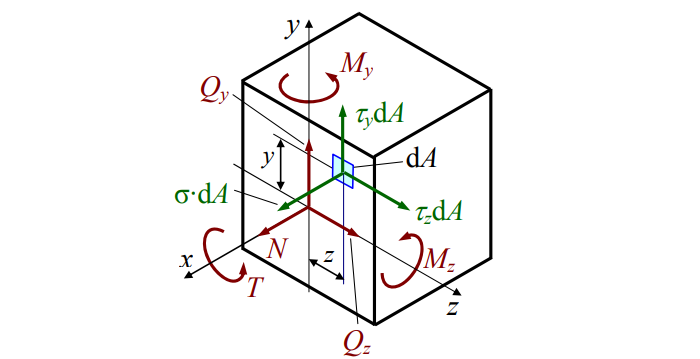
Распределив по осям, получим картину нагрузки сечения (см. рис. 4):
Нагрузки и деформации, изучаемые в сопромате
Изучим несколько принятых терминов.
Напряжения
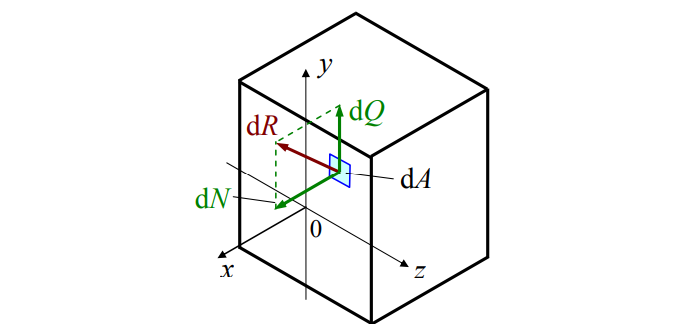
В теле приложенные силы распределяются по сечению. Нагружен каждый элементарный «кусочек». Разложим силы:
Элементарные усилия таковы:
σ – «сигма», нормальное напряжение. Перпендикулярно сечению. Характерно для сжатия / растяжения;
τ – «тау», касательное напряжение. Параллельно сечению. Появляется при кручении;
p – полное напряжение.
Просуммировав элементы, получим:
N – нормальная сила;
A – площадь сечения.
В принятой в России системе СИ сила измеряется в ньютонах (Н). Напряжения – в паскалях (Па). Длины в метрах (м).
Деформации
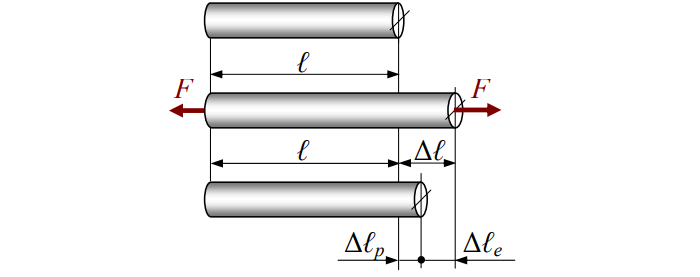
Различают деформацию упругую (с индексом «e») и пластическую (с индексом «p»). Первая исчезает по снятии растягивающей / сжимающей силы, вторая – нет.
Полная деформация будет равна:
Деформация относительная обозначается «ε» и рассчитывается так:
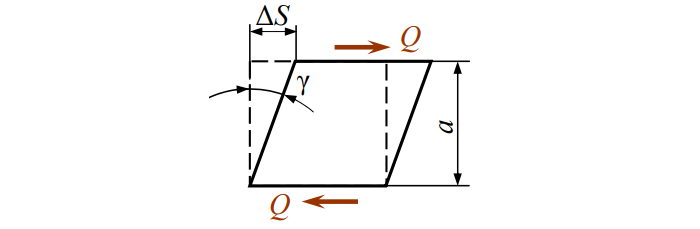
Под «сдвигом» понимается смещение параллельных слоев. Рассмотрим рисунок:
Здесь γ – относительный сдвиг.
Виды нагрузки
Растяжение и сжатие – нагрузка нормальной силой (по оси стержня).
Кручение – действует момент. Обычно рассчитываются передающие усилия валы.
Изгиб – воздействие направлено на искривление.
Основные формулы
Базовый принцип сопромата единственный. В упомянутой задаче о пружине применим закон Гука:
E – модуль упругости (Юнга). Величина зависит от используемого материала. Для стали полагают равным 200 х 10 6 Па.
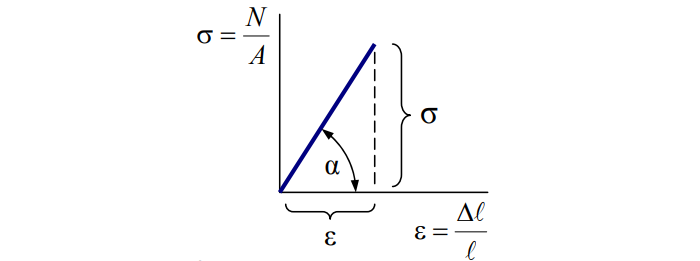
Сопротивление материала прямо пропорционально деформации:
Закон верен не всегда и не для всех материалов. Как уже упоминалось, принимается как одно из допущений.
Реальная диаграмма
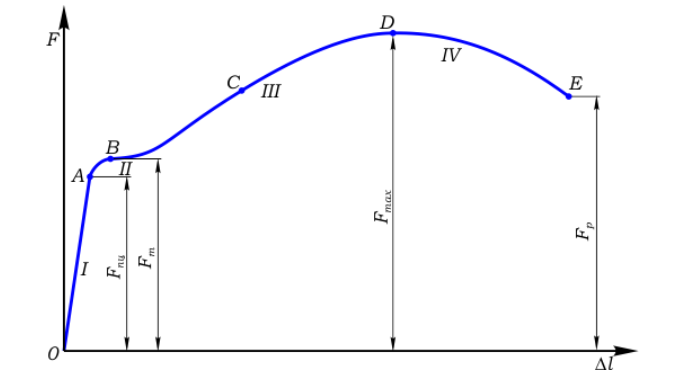
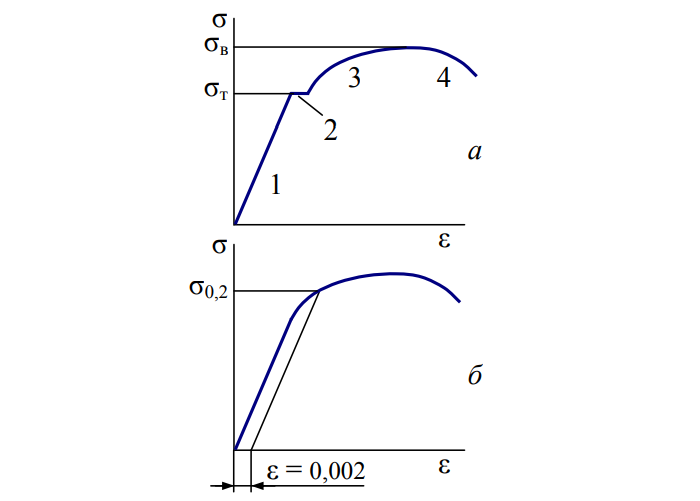
Растяжение стержня из низкоуглеродистой стали выглядит следующим образом:
График (б) относится к большей части конструкционных материалов: подкаленные стали, сплавы цветных металлов, пластики.
Расчеты обычно ведут по σт (а) и σ0.2 (б). С незначительными пластическими деформациями конструкции или без таковых.
Пример решения задачи
Какой груз допустимо подвесить на пруток из стали 45 Ø10 мм?
σ0,2 для стали 45 равна 245 МПа (из ГОСТ).
Площадь сечения прутка:
Допустимая сила тяжести:
Для получения веса следует разделить на ускорение свободного падения g:
Ответ: необходимо подвесить груз массой 1950 кг.
Как найти опасное сечение
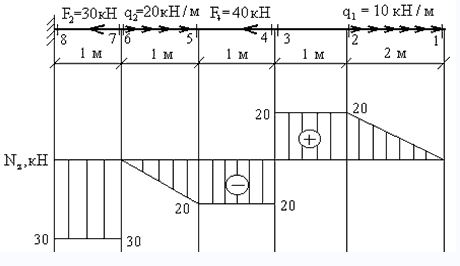
Наиболее простой способ – построение эпюры. На закрепленную балку действуют точечные и распределенные силы. Считаем на характерных участках, начиная с незакрепленного конца.
Усилие положительно, если направлено на растяжение.
На схеме показано, что:
Зачем и кому нужен сопромат
Даже не имеющий отношения к прочностным расчетам инженер-универсал должен иметь понятие о приблизительных (на 10-20%) значениях. Знать конструкционные материалы, представлять свойства. Чувствовать заранее слабые места агрегатов.
Совершенно необходим разработчикам различных конструкций, машиностроительных изделий. Будущим архитекторам в вузах преподается в виде предмета «Строительная механика».
Методика помогает на стадии проектирования обеспечивать необходимый запас прочности изделий. Стойкость к постоянным и динамичным нагрузкам. Это сберегает массу времени и затрат в дальнейших изготовлении, испытании и эксплуатации изделия. Обеспечивает надежность и долговечность.