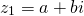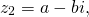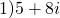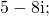Что такое сопряженные комплексные числа

Комплексно-сопряженные числа

Что такое комплексно-сопряженные числа? Как комплексно-сопряженные числа изображаются на комплексной плоскости?

у которых действительные части равны, а коэффициенты при мнимой части — противоположные числа, называются комплексно-сопряженными.

(другими словами, комплексонов-сопряженные числа — это комплексные числа, которые отличаются только знаком при мнимой части).

Примеры комплексно-сопряженных чисел:

Свойства комплексно сопряженных чисел

1) Действительное число является комплексно-сопряженным самому себе, так как a+0i=a-0i.

2) Сумма комплексно- сопряженных чисел — действительное число:

3) Разность комплексно-сопряженных чисел — мнимое число:

4) Произведение комплексно-сопряженных чисел — действительное число:

Изображение комплексно-сопряженных чисел на плоскости

На комплексной плоскости z1=a+bi и z2=a-bi изображаются

1) точками, симметричными относительно действительной оси ox.

Например, z1= — 6+3i и z2= — 6-3i; z3=0+2i и z4=0-2i; z5=5+0i и z6=5-0i.

2) векторами, симметричными относительно действительной оси ox.

Например, z1= 0+4i и z2= 0-4i; z3= 5+2i и z4= 5-2i; z5= — 6+0i и z6=- 6-0i.

Источник

Комплексные числа

Алгебраическая форма записи комплексных чисел

Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме

Комплексно сопряженные числа

Модуль комплексного числа

Деление комплексных чисел, записанных в алгебраической форме

Изображение комплексных чисел радиус-векторами на координатной плоскости

Аргумент комплексного числа

Тригонометрическая форма записи комплексного числа

Формула Эйлера. Экспоненциальная форма записи комплексного числа

Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме

Извлечение корня натуральной степени из комплексного числа

Алгебраическая форма записи комплексных чисел

Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.

Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.

Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме

Комплексно сопряженные числа

Модуль комплексного числа

Модулем комплексного числа z = x + i y называют вещественное число, обозначаемое | z | и определенное по формуле

Для произвольного комплексного числа z справедливо равенство:

а для произвольных комплексных чисел z₁ и z₂ справедливы неравенства:

Деление комплексных чисел, записанных в алгебраической форме

Деление комплексного числа z₁ = x₁ + i y₁ на отличное от нуля комплексное число z₂ = x₂ + i y₂ осуществляется по формуле

Используя обозначения модуля комплексного числа и комплексного сопряжения, частное от деления комплексных чисел можно представить в следующем виде:

Деление на нуль запрещено.

Изображение комплексных чисел радиус-векторами координатной плоскости

Рассмотрим плоскость с заданной на ней прямоугольной декартовой системой координат Oxy и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.

При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.

Аргумент комплексного числа

Считается, что комплексное число нуль аргумента не имеет.

Тогда оказывается справедливым равенство:

(3)

(4)

а аргумент определяется в соответствии со следующей Таблицей 1.

Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом k обозначать в Таблице 1 произвольное целое число.

Таблица 1. – Формулы для определения аргумента числа z = x + i y

y z

Расположение числа z	Знаки x и y	Главное значение аргумента	Аргумент	Примеры
Положительная вещественная полуось
Положительная мнимая полуось
Второй квадрант
Отрицательная вещественная полуось	Положительная вещественная полуось
Знаки x и y
Главное значение аргумента	0
Аргумент	φ = 2kπ
Примеры

Главное
значение
аргументаАргументПримерыГлавное
значение
аргументаАргументПримерыГлавное
значение
аргументаАргументПримеры

x zТретий
квадрантЗнаки x и y

x zОтрицательная
мнимая
полуосьЗнаки x и y

y zЧетвёртый
квадрантЗнаки x и y

Положительная вещественная полуось

Главное значение аргумента:

Расположение числа z :

Главное значение аргумента:

Расположение числа z :

Положительная мнимая полуось

Главное значение аргумента:

Расположение числа z :

Главное значение аргумента:

Расположение числа z :

Отрицательная вещественная полуось

Отрицательная мнимая полуось

x z = x + i y может быть записано в виде

Формула Эйлера. Экспоненциальная форма записи комплексного числа

В курсе «Теория функций комплексного переменного», который студенты изучают в высших учебных заведениях, доказывается важная формула, называемая формулой Эйлера :

Из формулы Эйлера (6) и тригонометрической формы записи комплексного числа (5) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде

Из формулы (7) вытекают, в частности, следующие равенства:

а из формул (4) и (6) следует, что модуль комплексного числа

Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме

Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.

Действительно, умножение и деление двух произвольных комплексных чисел и записанных в экспоненциальной форме, осуществляется по формулам

Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.

При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.

Возведение комплексного числа z = r e iφ в натуральную степень осуществляется по формуле

Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.

Извлечение корня натуральной степени из комплексного числа

Пусть — произвольное комплексное число, отличное от нуля.

Для того, чтобы решить уравнение (8), перепишем его в виде

следствием которых являются равенства

(9)

Из формул (9) вытекает, что уравнение (8) имеет n различных корней

(10)

то по формуле (10) получаем:

Источник

Комплексно сопряженные числа

Вы будете перенаправлены на Автор24

Выписать действительную и мнимую части для заданных комплексных чисел:

Комплексная плоскость

Любое комплексное число можно изобразить на плоскости, которую принято называть комплексной плоскостью. Комплексная плоскость аналогична прямоугольной декартовой системе координат, исключение составляют только названия осей:

Общий вид комплексной плоскости представлен на рис.1.

Готовые работы на аналогичную тему

Зная действительную и мнимую части комплексного числа, записать данное число:

Зная действительную и мнимую части комплексного числа, изобразить данное число на комплексной плоскости:

Записать комплексно-сопряженные числа для заданных комплексных чисел:

Отмечая соответствующие точки на плоскости, получим изображение комплексных чисел (рис.3)

Если комплексное число изображается точкой на вещественной оси, то комплексно-сопряженное число изображается той же самой точкой.

Изобразить на комплексной плоскости числа комплексно-сопряженные к отмеченным.

Изображая комплексно-сопряженные числа на комплексной плоскости, воспользуемся примечаниями 1 и 2.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 11 11 2021

Источник

Комплексно сопряженные числа

Сопряженное (или комплексно сопряженное) число с комплексным числом \(\ z=x+i y \) является числом \(\ \overline=x-i y \)

поиска для комплексного числа \(\ z=-34-i \) является его сопряженное число.

Следовательно, сопряженное число имеет вид: \(\ \overline=-34+i \)

На комплексной плоскости сопряженные числа зеркалируются относительно оси действительных чисел.

Свойства комплексно-сопряженных чисел

1. \(\ |z|=|z| \), т. е. модули сопряженных чисел равны.

Модуль комплексного числа \(\ z=-4+i \) равен \(\ r=\sqrt<(-4)^<2>+1^<2>>=\sqrt <17>\). Присоединенным к комплексному числу является число \(\ z=-4-i \), модуль \(\ r=\sqrt<(-4)^<2>+(-1)^<2>>=\sqrt <17>\) которого равен модулю исходного числа.

2. \(\ \arg z=-\arg \overline \) т. е. Аргументы сопряженных чисел различаются по знаку.

3. \(\ \overline<\overline>=z \) т. е. Комплексное сопряженное сопряженное число является исходным комплексным числом.

4. \(\ z \cdot \overline=|z|^ <2>\) т. е. В результате произведения сопряженных чисел получается вещественное число.

5.\(\ z+\overline=2 \operatorname z \) т. е. Сумма сопряженных чисел также является вещественным числом.

6.\(\ \overline \cdot z_<2>>=\overline> \cdot \overline> \) т. е. Сопряженное произведение двух комплексных чисел является произведением их сопряженных чисел.

7.\(\ \overline \div z_<2>>=\overline> \div \overline> \) т. е. Сопряженное к ним частное число есть фактор сопряженного.

Примеры решения проблем

Чтобы умножить комплексное число \(\ z=4-7 i \) на его сопряженное.

\(\ z \cdot \overline=(4-7 i) \cdot(4+7 i)=4 \cdot 4+(-7) \cdot 7 \cdot i^<2>+i(4 \cdot 7-7 \cdot 4)=65 \)

Чтобы найти сопряженное к частному два комплексных числа: \(\ z 1=1-3 i \), \(\ z 2=2+5 i \).

Фактор комплексных чисел определяется путем умножения числителя и знаменателя на сопряженное число:

Мы получим тот же результат, если найдем фактор сопряженных чисел \(\ z \rceil=1-3 i \), \(\ z 2=2+5 i \):

Источник

Что такое сопряженные комплексные числа

Определение. Два комплексных числа, имеющие одну и ту же действительную часть и взаимно противоположные коэффициенты мнимых частей, называются взаимно) сопряженными.

Для любого комплексного числа z существует одно и только одно сопряженное с ним комплексное число, которое обозначается . Если , то . Очевидно, тогда и только тогда, когда z — действительное число.

Отметим, что сумма и произведение двух сопряженных комплексных чисел являются действительными числами:

Ранее было выведено правило деления комплексных чисел. Это правило можно проще получить с помощью сопряженных комплексных чисел.

Умножим числитель и знаменатель дроби — на число комплексно сопряженное со знаменателем. Выполнив действия и отделив действительную часть от мнимой, получаем:

Этот результат совпадает с формулой, полученной в п. 6.

Эту формулу можно не запоминать, а только помнить, что при делении надо числитель и знаменатель дроби умножить на число, комплексно сопряженное со знаменателем.

Теорема 1. Число, сопряженное с суммой или произведением комплексных чисел, есть сумма или соответственно произведение чисел, сопряженных данным комплексным числам:

Доказательство. Пусть . Тогда . Имеем:

Эта теорема показывает, что, поставив в соответствие каждому комплексному числу сопряженное с ним число, мы получили взаимно однозначное отображение поля комплексных чисел К на это же поле при котором сохраняются операции сложения и умножения.

Из теоремы 1 непосредственно вытекает следующее

Следствие 1. Число, сопряженное (натуральной) степени комплексного числа, равно той же степени числа, сопряженного данному:

Далее, если нам дан многочлен

коэффициенты которого — комплексные числа, то, заменив каждый коэффициент сопряженным ему комплексным числом мы получим новый многочлен, который обозначим через

Если теперь в полученном многочлене произвольное значение переменной заменить сопряженным ему значением то в силу доказанной выше теоремы и следствия I полученное значение многочлена будет комплексным числом, сопряженным с исходным значением многочлена

Если, в частности, все коэффициенты многочлена действительные числа, то один и тот же многочлен, и формула (3) дает:

Таким образом, мы получили

Следствие 2. При замене в многочлене с действительными коэффициентами произвольного значения аргумента сопряженным ему числом значение многочлена также заменяется сопряженным ему числом.

Источник