Что такое совершенная дизъюнктивная нормальная форма
Для всякой логической формулы с помощью тождественных преобразований можно построить бесконечно много равносильных ей формул. В алгебре логики одной из основных задач является поиск канонических форм (т. е. формул, построенных по единому правилу, канону).
Если логическая функция выражена через дизъюнкцию, конъюнкцию и отрицание переменных, то такая форма представления называется нормальной.
Среди нормальных форм выделяются совершенные нормальные формы (такие формы, в которых функции записываются единственным образом).
Совершенная дизъюнктивная нормальная форма (СДНФ)
Определение. Формулу называют элементарной конъюнкцией, если она образованна конъюнкцией некоторого числа переменных или их отрицаний.
Определение. Формула называтся дизъюнктивной нормальной формой (ДНФ), если она является дизъюнкцией неповторяющихся элементарных конъюнкций.
Определение. Логическая формула от k переменных называется совершенной дизъюнктивной нормальной формой (СДНФ), если:
1) формула является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция k переменных х1, х2, …, хk, причем на i-м месте этой конъюнкции стоит либо переменная хi, либо ее отрицание;
2) все элементарные конъюнкции в такой ДНФ попарно различны.
Совершенная конъюнктивная нормальная форма (СКНФ)
Определение. Формулу называют элементарной дизъюнкцией, если она образована дизъюнкцией некоторого числа переменных или их отрицаний.
Определение. Формула называется конъюнктивной нормальной формой (КНФ), если она является конъюнкцией неповторяющихся элементарных дизъюнкций.
Определение. Логическая формула от k переменных называется совершенной конъюнктивной нормальной формой (КДНФ), если:
1) формула является КНФ, в которой каждая элементарная дизъюнкция есть дизъюнкция k переменных х1, х2, …, хk, причем на i-м месте этой дизъюнкции стоит либо переменная хi, либо ее отрицание;
2) все элементарные дизъюнкции в такой КНФ попарно различны.
Алгоритм построения СДНФ по таблице истинности
Алгоритм построения СКНФ по таблице истинности
Пример: Дана таблица истинности логической функции от трех переменных. Построить логическую формулу, реализующую эту функцию.
| x | y | z | F (x, y, z) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Т.к. на большинстве строк таблицы истинности значение функции равно 1, то построим СКНФ. В результате получим следующую логическую формулу:
F = (¬ x ∨ y ∨ z) ∧ (¬ x ∨ y ∨ ¬ z)
Проверим полученную формулу. Для этого построим таблицу истинности функции.
| x | y | z | ¬ x | ¬ x ∨ y ∨ z | ¬ z | ¬ x ∨ y ∨ ¬ z | F (x, y, z) |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
Сравнив исходную таблицу истинности и построенную для логической формулы, заметим, что столбцы значений функции совпадают. Значит, логическая функция построена верно.
Copyright © 2014-2021, Урок информатики
Все права защищены
Совершенная нормальная форма — дизъюнктивная и конъюнктивная, правило построения
Что такое СДНФ
Нормальная форма логической формулы характеризуется тем, что для нее не свойственны эквивалентность, отрицание формул неэлементарного типа и знаки импликации.
Существует две формы нормального типа: КНФ (конъюнктивная нормальная форма) и ДНФ (дизъюнктивная нормальная форма).
СДНФ — совершенная дизъюнктивная нормальная форма формулы. СДНФ — способ написания функции алгебры логики в качестве логического выражения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
СДНФ формулы — это равнозначная ей формула, которая представляет собой дизъюнкцию элементарных конъюнкций, при которых функция достигает показателя «1».
ДНФ выглядит следующим образом:
СДНФ обладает некоторыми определенными свойствами:
К СДНФ возможно привести любую формулу алгебры логики. Исключение составляет только тождественно ложная формула. СДНФ можно получить как используя таблицы истинности, так и через равносильные преобразования.
При построении таблицы истинности важно помнить, что логические переменные со значением «0» необходимо брать с отрицанием.
Что такое СКНФ
СКНФ — совершенная конъюнктивная нормальная форма. Формулу можно назвать таковой, когда она — конъюнкция неповторяющихся элементарных дизъюнкций.
Формула должна соответствовать нескольким условиям, чтобы называться СКНФ:
Правила построения по таблице истинности
Дизъюнктивная форма
Если функция равна 1, то для всех наборов переменных, при которых это происходит, записывается произведение. Однако переменные, которые имеют значение 0, берутся с отрицанием.
Конъюнктивная форма
Когда функция равна 0, то для всех наборов переменных, при которых это происходит, записывается сумма. Однако переменные, которые имеют значение 1, берутся с отрицанием.
Алгоритм приведения к СДНФ и СКНФ
Рассмотрим логическую функцию в виде таблицы истинности.
Алгоритм построения СДНФ по таблице истинности выглядит следующим образом:
Построим совершенную ДНФ:
И как результат получим следующую СДНФ:
Алгоритм построения СКНФ по таблице истинности выглядит следующим образом:
Построим совершенную КНФ:
И как результат получим следующую СКНФ:
Рассмотрев алгоритмы построения СДНФ и СКНФ ясно, что в случае подавляющей части наборов значений переменных функция равна 0, то значительно легче построить и СДНФ для получения ее формулы, а в обратном случае — СКНФ.
Доказательство эквивалентности
Доказать эквивалентность формул можно двумя способами.
Далее следуют примеры с некоторыми эквивалентными преобразованием в булевой алгебре и новыми эквивалентностями, которые возможно получить с их помощью.
Поглощение
Склеивание
Обобщенное склеивание
\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\)
\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\;\vee\;xyz\;\vee\;xy\overline z\;=\;xz\;\vee\;y\overline z\)
Расщепление
\(x\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;xy\;\vee\;\overline xy\;=\;x\;\cdot\;l\;\;\vee\;y\;\cdot\;l\;=\;x\;\vee\;y\)
Примеры с решением
Задача №1
Через применение закона де Моргана и правила \( x\;\rightarrow\;y\;=\;\overline x\;\vee\;y\) упростим выражения:
\(F\;=\;((((A\;\rightarrow\;B)\;\rightarrow\;\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;(((\overline A\;\vee\;B)\;\rightarrow\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\overline C\;)\;=\)
\(=\;((((\overline A\;\vee\;B)\;\rightarrow\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;((\overline<((\overline A\;\vee\;B)>\;\vee\;\overline A)\;\rightarrow\overline B)\;\rightarrow\overline C)\;=\)
\(=(((\overline A\;\vee\;B)\;\vee\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\;\overline C)\;=((\overline<(\overline<(\overline A\vee B)>\;\vee\;\overline A\;)>\;\vee\;\overline B)\;\rightarrow\;\overline C)\;=\)
\(=\;((\overline<(\overline A\;\vee\;B)>\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge B)\;\vee\;\overline C\;=\)
\(=((A\overline B\;\vee\;\overline A)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\)
\(=\;((A\overline B\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(A\overline BB\;\vee\;\overline AB)\;\vee\;\overline C\;=\;(0\;\vee\;\overline AB)\;\vee\;\overline C\;=\;\overline AB\;\vee\;\overline C\)
Далее приведем выражение к КНФ:
\(F\;=\;\overline AB\;\vee\;\overline C\;\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\)
Далее приведем выражение к СКНФ:
\(F\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\;=\;(\overline A\;\vee\:\overline C\;\vee\;B\overline B)\;\wedge\;(A\overline A\;\vee\;B\;v\;\overline C)\;=\)
\(=\;(\overline A\;\vee\;\overline C\;\vee\;B)\;\wedge\;(A\;\vee\;B\;\vee\;\overline C)\;\wedge\;(\overline A\;\vee\;\overline C\;\vee\;\overline B)\;\wedge\;(\overline A\;\vee\;B\;\;\overline C)\)
Задача №2
Используя эквивалентные преобразования, постройте ДНФ функции \(f(\widetilde x^n)\)
\(f(\widetilde x^3) = (\overline
\(f(\widetilde x^3) = (\overline
\(=(\overline
СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице
СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице
СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице
Простой конъюнкцией или конъюнктом называется конъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная встречается не более одного раза.
ДНФ — нормальная форма, в которой булева функция имеет вид дизъюнкции нескольких простых конъюнктов.
СДНФ — это такая ДНФ, которая удовлетворяет условиям:
Для любой булевой функции выполняется следующее соотношение, называемое разложением Шеннона.
Алгоритм построения СДНФ по таблице истинности
Пример построения СДНФ для медианы
В таблице истинности отмечаем те наборы переменных, на которых значение функции равно 1.
| x | y | z | $\langle x,y,z \rangle$ |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть 1, то в конъюнкцию включаем саму переменную, иначе ее отрицание.
Примеры СДНФ для некоторых функций
а > в ней нет одинаковых дизъюнктивных элементов;
б > ни одна элементарная конъюнкция не содержит двух одинаковых высказываний;
в > ни какая элементарная конъюнкция не содержит высказывание вместе с ее отрицанием;
Условие а > – г > являются необходимыми и достаточными для того, чтобы ДНФ стала СДНФ. В свою очередь эти условия дают возможность составить алгоритм получения СДНФ из ДНФ:
2) если в полученном выражении окажутся одинаковые элементарные конъюнкции, то лишние опускаются;
3) если в некоторых элементарных конъюнкциях окажутся одинаковые высказывания, то лишние опускаются;
4) удаляем элементарные конъюнкции, в которых содержатся высказывания вместе с их отрицанием.
Если все элементарные конъюнкции окажутся таковыми, т.е. вся формула будет ложной, то она не будет иметь СДНФ.
Если все элементарные конъюнкции окажутся таковыми, т.е. вся формула будет ложной, то она не будет иметь СДНФ.
Все элементарные конъюнкции в такой ДНФ попарно различны.
Совершенная дизъюнктивная нормальная форма представляет собой формулу, построенную по строго определенным правилам с точностью до порядка следования элементарных конъюнкций < дизъюнктивных членов >в ней.
Она является примером однозначного представления булевой функции в виде формульной < алгебраической >записи.
Алгоритм построения СДНФ по таблице истинности:
Далее:
Механические приложения тройного интеграла
Механические и физические приложения поверхностного интеграла первого рода
Свойства тройного интеграла
Вычисление двойного интеграла. Двукратный интеграл
Условия независимости криволинейного интеграла от пути интегрирования
Дифференциальные характеристики векторного поля
Критерий полноты <формулировка>. Лемма о нелинейной функции
Вычисление криволинейного интеграла первого рода. Примеры
Поток жидкости через поверхность
Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных
Выражение площади плоской области через криволинейный интеграл
Нормальные формы
Инвариантное определение дивергенции
Конспект урока в 10-м классе по информатике «Совершенная дизъюктивная нормальная форма и совершенная конъюктивная нормальная форма»
Оборудование: Презентация, слайды, которые демонстрируются на экран с помощью проектора (Приложение 1).
План урока для учителя
Содержание этапов урока
Виды и формы работы
I. Организационный момент. Приветствие учащихся
II. Мотивационное начало урока
Вспомним что такое логическая функция.
Логической функцией n переменных y = f(x1, x2, …, xn) называется такая функция, у которой все переменные и сама функция могут принимать только два значения: 0 и 1.
Задание: построить по формуле функциональную схему и таблицу истинности. Дана формула 
| X | Y |  |  |  |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 |
На практике при конструировании различных электронных устройств есть только таблица истинности. Возникает проблема – как от таблицы истинности перейти к логическому выражению – формуле, а на ее основе построить функциональную схему. Эту проблему мы сегодня и попробуем разрешить.
III. Объяснение нового материала
Мы знаем, что конъюнкция – это логическое умножение, а дизъюнкция – логическое сложение. Знаем, что переменные структурной формулы соответствуют входам функциональной схемы. Значения переменных в таблице истинности соответствуют значениям входов функциональной схемы.
Мы знаем, как составлять таблицу истинности для логической функции. Попробуем решить обратную задачу. Так мы решим возникшую проблему – как от таблицы истинности перейти к логическому выражению – формуле, а на ее основе построить функциональную схему.
Пусть дана таблица истинности для некоторой логической функции F(X,Y):
| X | Y | F |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Здесь нам помогут СКНФ и СДНФ. Что это такое? (Учитель сообщает тему урока).
“Совершенная дизъюнктивная нормальная форма и совершенная конъюнктивная нормальная форма”.
Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одном и том же порядке. (Слайд 8).
Перечислим свойства совершенства для СДНФ:
1. Каждое логическое слагаемое формулы содержит все переменные, входящие в функцию.
2. Все логические слагаемые различны.
3. Ни одно слагаемое не содержит одновременно переменную и ее отрицание.
4. Ни одно слагаемое не содержит одну и ту же переменную дважды.
Совершенной конъюнктивной нормальной формой (СКНФ) называется такая конъюнктивная нормальная форма, у которой в каждую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одном и том же порядке. (Слайд 9).
Решение задачи. (Слайды 11, 12)
Алгоритм получения СДНФ по таблице истинности:
1. Отметить те строки таблицы истинности, в последнем столбце которых стоят 1:
2. Выписать для каждой отмеченной строки конъюнкцию всех переменных следующим образом: если значение в данной строке равно 1, то в конъюнкцию включать саму эту переменную, если равно 0, то ее отрицание: для 1-й строки 


3. Все полученные конъюнкции связать в дизъюнкцию:
4. Упрощаем формулу, применяем законы логики.
Алгоритм получения СКНФ по таблице истинности
1. Отметить те строки таблицы истинности, в последнем столбце которых стоят 0:
2. Выписать для каждой отмеченной строки дизъюнкцию всех переменных следующим образом: если значение в данной строке равно 0, то в дизъюнкцию включать саму эту переменную, если равно 1, то ее отрицание: для 2-й строки 
3. Все полученные дизъюнкции связать в конъюнкцию:
4. Упрощаем формулу, применяем законы логики (если это необходимо).
Покажем, что полученные по двум алгоритмам СДНФ и СКНФ эквивалентны. СДНФ 
Можем проверить, построив таблицу истинности по найденной формуле.
Теперь построим логическую схему:
IV. Этап общения, систематизации знаний и закрепление изученного
Проблема решена, теперь мы знаем, как от таблицы истинности перейти к формуле, а на ее основе построить функциональную схему.
Решение задач по карточкам (задания разноуровневые). (Приложение 2).
Примечание: Для нахождения формулы по таблице истинности рекомендуется использовать тот из двух алгоритмов, в котором в таблице помечается меньше строк.
V. Подведение итогов, домашнее задание
Построение СКНФ и СДНФ по таблице истинности
Вы будете перенаправлены на Автор24
Нормальная форма логической формулы не содержит знаков импликации, эквивалентности и отрицания неэлементарных формул.
Нормальная форма существует в двух видах:
не содержит одинаковых элементарных дизъюнкций;
ни одна из дизъюнкций не содержит одинаковых переменных;
каждая элементарная дизъюнкция содержит каждую переменную из входящих в данную КНФ.
Любая булева формула, которая не является тождественно истинной, может быть представлена в СКНФ.
Правила построения СКНФ по таблице истинности
Для каждого набора переменных, при котором функция равна 0, записывается сумма, причем переменные, которые имеют значение 1, берутся с отрицанием.
не содержит одинаковых элементарных конъюнкций;
ни одна из конъюнкций не содержит одинаковых переменных;
каждая элементарная конъюнкция содержит каждую переменную из входящих в данную ДНФ, к тому же в одинаковом порядке.
Любая булева формула, которая не является тождественно ложной, может быть представлена в СДНФ, к тому же единственным образом.
Правила построения СДНФ по таблице истинности
Для каждого набора переменных, при котором функция равна 1, записывается произведение, причем переменные, которые имеют значение 0 берут с отрицанием.
Примеры нахождения СКНФ и СДНФ
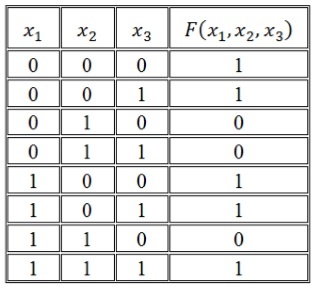
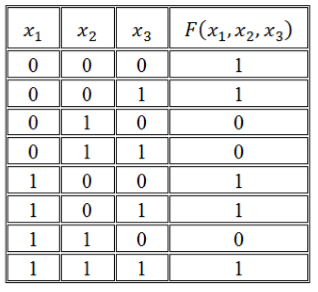
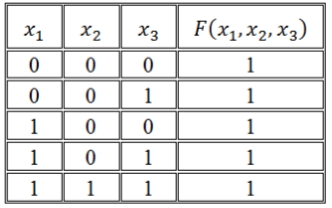
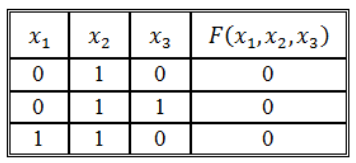
Записать логическую функцию по ее таблице истинности:
Решение:
Воспользуемся правилом построения СДНФ:
\[F\left(x_1,\ x_2,\ x_3\right)=\left(\overline
Воспользуемся правилом построения СКНФ:
\[F\left(x_1,\ x_2,\ x_3\right)=\left(x_1\vee \overline
Готовые работы на аналогичную тему
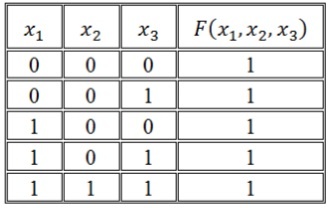
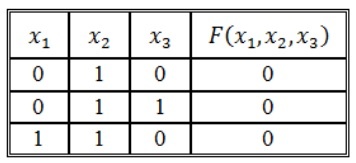
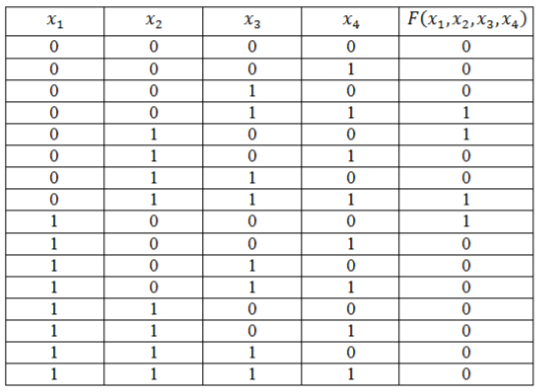
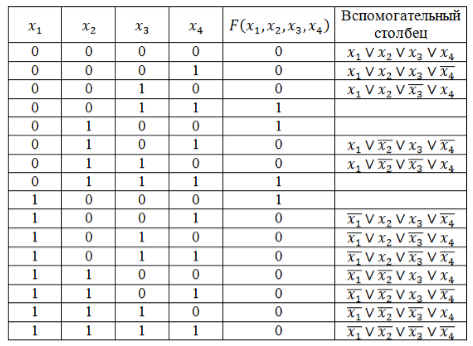
Функция задана таблицей истинности:
Представить эту функцию в виде СДНФ и СКНФ.
Решение:
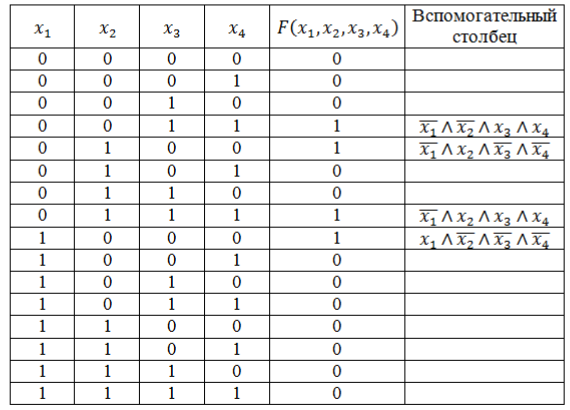
Запишем логическую функцию в СДНФ. Для удобства решения добавим к таблице вспомогательный столбец.
Используя правило составления СДНФ не забываем вводить знак отрицания для переменных со значением 0. Инвертировать нулевые значения переменных обязательно, т.к. иначе они превратят значения конъюнкций в нули основной функции.
Полученные во вспомогательном столбце конъюнкции соединим знаком дизъюнкции и получим искомую логическую функцию в виде СДНФ:
\[F\left(x_1,x_2,x_3,x_4\right)=\left(\overline
Запишем логическую функцию в СКНФ.
Используя правило составления СКНФ не забываем вводить знак отрицания для переменных со значением 1. Инвертировать единичные значения переменных обязательно, т.к. иначе они превратят значения дизъюнкций в единицы основной функции.
Полученные во вспомогательном столбце дизъюнкции соединим знаком конъюнкции и получим искомую логическую функцию в виде СКНФ:
\[F\left(x_1,x_2,x_3,x_4\right)=\left(x_1\vee x_2\vee x_3\vee x_4\right)\wedge \left(x_1\vee x_2\vee x_3\vee \overline