Что такое совершенная конъюнктивная нормальная форма

27.10.202329.04.2022 admin 0 Comments

Что такое совершенная конъюнктивная нормальная форма

Определение:

Конъюнктивная нормальная форма, КНФ (англ. conjunctive normal form, CNF) — нормальная форма, в которой булева функция имеет вид конъюнкции нескольких простых дизъюнктов.

Пример КНФ: [math]f(x,y,z) = (x \lor y) \land (y \lor \neg)[/math]

СКНФ [ править ]

Пример СКНФ: [math]f(x,y,z) = (x \lor \neg \lor z) \land (x\lor y \lor \neg)[/math]

Последнее выражение и является СКНФ. Так как СКНФ получена из СДНФ, которая может быть посторена для любой функции, не равной тождественному нулю, то теорема доказана.[math]\triangleleft[/math]

Алгоритм построения СКНФ по таблице истинности [ править ]

Пример построения СКНФ для медианы [ править ]

Построение СКНФ для медианы от трех аргументов [ править ]

0	0	0	0
x	y	z	[math] \langle x,y,z \rangle [/math]
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

0	0	0	0	[math]( x \lor y \lor z)[/math]
x	y	z	[math] \langle x,y,z \rangle [/math]
0	0	1	0	[math]( x \lor y \lor \neg)[/math]
0	1	0	0	[math](x \lor \neg \lor z)[/math]
0	1	1	1
1	0	0	0	[math](\neg \lor y \lor z)[/math]
1	0	1	1
1	1	0	1
1	1	1	1

3. Все полученные дизъюнкции связываем операциями конъюнкции.

[math] \langle x,y,z \rangle = ( x \lor y \lor z) \land (\neg \lor y \lor z) \land (x \lor \neg \lor z) \land ( x \lor y \lor \neg)[/math]

Построение СКНФ для медианы от пяти аргументов [ править ]

0	0	0	0	0	0	[math](x_1 \lor x_2 \lor x_3 \lor x_4 \lor x_5)[/math]
[math] x_1 [/math]	[math] x_2 [/math]	[math] x_3 [/math]	[math]x_4[/math]	[math] x_5 [/math]	[math] \langle x_1, x_2, x_3, x_4, x_5 \rangle [/math]
0	0	0	0	1	0	[math](x_1 \lor x_2 \lor x_3 \lor x_4 \lor \neg )[/math]
0	0	0	1	0	0	[math](x_1 \lor x_2 \lor x_3 \lor \neg \lor x_5)[/math]
0	0	0	1	1	0	[math](x_1 \lor x_2 \lor x_3 \lor \neg \lor \neg )[/math]
0	0	1	0	0	0	[math](x_1 \lor x_2 \lor \neg \lor x_4 \lor x_5)[/math]
0	0	1	0	1	0	[math](x_1 \lor x_2 \lor \neg \lor x_4 \lor \neg )[/math]
0	0	1	1	0	0	[math](x_1 \lor x_2 \lor \neg \lor \neg \lor x_5)[/math]
0	0	1	1	1	1
0	1	0	0	0	0	[math](x_1 \lor \neg \lor x_3 \lor x_4 \lor x_5)[/math]
0	1	0	0	1	0	[math](x_1 \lor \neg \lor x_3 \lor x_4 \lor \neg )[/math]
0	1	0	1	0	0	[math](x_1 \lor \neg \lor x_3 \lor \neg \lor x_5)[/math]
0	1	0	1	1	1
0	1	1	0	0	0	[math](x_1 \lor \neg \lor \neg \lor x_4 \lor x_5)[/math]
0	1	1	0	1	1
0	1	1	1	0	1
0	1	1	1	1	1
1	0	0	0	0	0	[math](\neg \lor x_2 \lor x_3 \lor x_4 \lor x_5)[/math]
1	0	0	0	1	0	[math](\neg \lor x_2 \lor x_3 \lor x_4 \lor \neg )[/math]
1	0	0	1	0	0	[math](\neg \lor x_2 \lor x_3 \lor \neg \lor x_5)[/math]
1	0	0	1	1	1
1	0	1	0	0	0	[math](\neg \lor x_2 \lor \neg \lor x_4 \lor x_5)[/math]
1	0	1	0	1	1
1	0	1	1	0	1
1	0	1	1	1	1
1	1	0	0	0	0	[math](\neg \lor \neg \lor x_3 \lor x_4 \lor x_5)[/math]
1	1	0	0	1	1
1	1	0	1	0	1
1	1	0	1	1	1
1	1	1	0	0	1
1	1	1	0	1	1
1	1	1	1	0	1
1	1	1	1	1	1

[math] \langle x_1, x_2, x_3, x_4, x_5 \rangle = (x_1 \lor x_2 \lor x_3 \lor x_4 \lor x_5) \land (x_1 \lor x_2 \lor x_3 \lor x_4 \lor \overline ) \land \\ (x_1 \lor x_2 \lor x_3 \lor \overline \lor x_5) \land (x_1 \lor x_2 \lor x_3 \lor \overline \lor \overline ) \land (x_1 \lor x_2 \lor \overline \lor x_4 \lor x_5) \land \\ (x_1 \lor x_2 \lor \overline \lor x_4 \lor \overline ) \land (x_1 \lor x_2 \lor \overline \lor \overline \lor x_5) \land (x_1 \lor \overline \lor x_3 \lor x_4 \lor x_5) \land \\ (x_1 \lor \overline \lor x_3 \lor x_4 \lor \overline ) \land (x_1 \lor \overline \lor x_3 \lor \overline \lor x_5) \land (x_1 \lor \overline \lor \overline \lor x_4 \lor x_5) \land (\overline \lor x_2 \lor x_3 \lor x_4 \lor x_5) \land (\overline \lor x_2 \lor x_3 \lor x_4 \lor \overline ) \land (\overline \lor x_2 \lor x_3 \lor \overline \lor x_5) \land (\overline \lor x_2 \lor \overline \lor x_4 \lor x_5) \land (\overline \lor \overline \lor x_3 \lor x_4 \lor x_5) [/math]

Примеры СКНФ для некоторых функций [ править ]

Стрелка Пирса: [math] x \downarrow y = (\neg \lor ) \land ( \lor \neg ) \land (\neg \lor \neg ) [/math]

Исключающее или: [math] x \oplus y \oplus z = (\neg \lor \neg \lor z) \land (\neg \lor y \lor \neg ) \land (x \lor \neg \lor \neg ) \land (x \lor y \lor z)[/math]

Источник

Построение СКНФ и СДНФ по таблице истинности

Вы будете перенаправлены на Автор24

Нормальная форма логической формулы не содержит знаков импликации, эквивалентности и отрицания неэлементарных формул.

Нормальная форма существует в двух видах:

не содержит одинаковых элементарных дизъюнкций;

ни одна из дизъюнкций не содержит одинаковых переменных;

каждая элементарная дизъюнкция содержит каждую переменную из входящих в данную КНФ.

Любая булева формула, которая не является тождественно истинной, может быть представлена в СКНФ.

Правила построения СКНФ по таблице истинности

Для каждого набора переменных, при котором функция равна 0, записывается сумма, причем переменные, которые имеют значение 1, берутся с отрицанием.

не содержит одинаковых элементарных конъюнкций;

ни одна из конъюнкций не содержит одинаковых переменных;

каждая элементарная конъюнкция содержит каждую переменную из входящих в данную ДНФ, к тому же в одинаковом порядке.

Любая булева формула, которая не является тождественно ложной, может быть представлена в СДНФ, к тому же единственным образом.

Правила построения СДНФ по таблице истинности

Для каждого набора переменных, при котором функция равна 1, записывается произведение, причем переменные, которые имеют значение 0 берут с отрицанием.

Примеры нахождения СКНФ и СДНФ

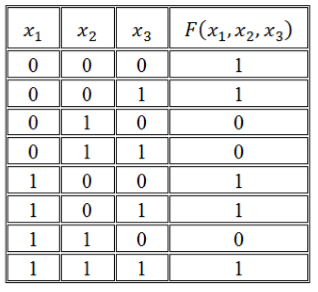
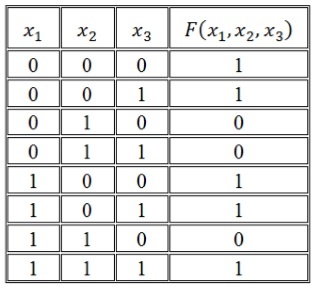
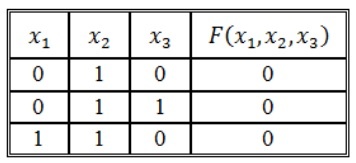
Записать логическую функцию по ее таблице истинности:

Решение:

Воспользуемся правилом построения СДНФ:

\[F\left(x_1,\ x_2,\ x_3\right)=\left(\overline\wedge \overline\wedge \overline\right)\vee \left(\overline\wedge \overline\wedge x_3\right)\vee \left(x_1\wedge \overline\wedge \overline\right)\vee \left(x_1\wedge \overline\wedge x_3\right)\vee \left(x_1\wedge x_2\wedge x_3\right)\]

Воспользуемся правилом построения СКНФ:

\[F\left(x_1,\ x_2,\ x_3\right)=\left(x_1\vee \overline\vee x_3\right)\wedge \left(x_1\vee \overline\vee \overline\right)\wedge \left(\overline\vee \overline\vee x_3\right)\]

Готовые работы на аналогичную тему

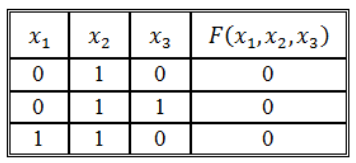
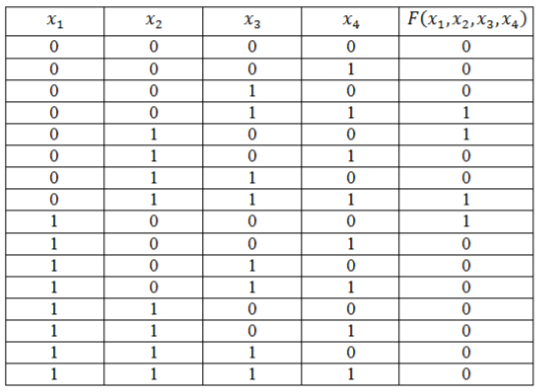
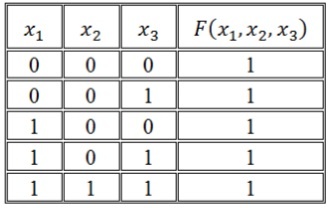
Функция задана таблицей истинности:

Представить эту функцию в виде СДНФ и СКНФ.

Решение:

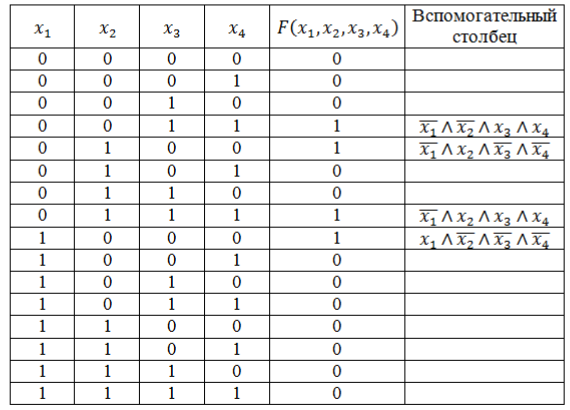
Запишем логическую функцию в СДНФ. Для удобства решения добавим к таблице вспомогательный столбец.

Используя правило составления СДНФ не забываем вводить знак отрицания для переменных со значением 0. Инвертировать нулевые значения переменных обязательно, т.к. иначе они превратят значения конъюнкций в нули основной функции.

Полученные во вспомогательном столбце конъюнкции соединим знаком дизъюнкции и получим искомую логическую функцию в виде СДНФ:

\[F\left(x_1,x_2,x_3,x_4\right)=\left(\overline\wedge \overline\wedge z\wedge f\right)\vee \left(\overline\wedge x_2\wedge \overline\wedge \overline\right)\vee \left(\overline\wedge x_2\wedge x_3\wedge x_4\right)\vee \left(x_1\wedge \overline\wedge \overline\wedge \overline\right).\]

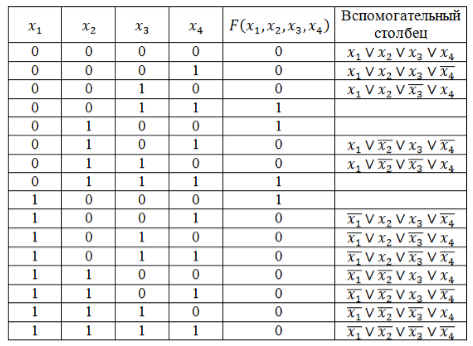
Запишем логическую функцию в СКНФ.

Используя правило составления СКНФ не забываем вводить знак отрицания для переменных со значением 1. Инвертировать единичные значения переменных обязательно, т.к. иначе они превратят значения дизъюнкций в единицы основной функции.

Полученные во вспомогательном столбце дизъюнкции соединим знаком конъюнкции и получим искомую логическую функцию в виде СКНФ:

\[F\left(x_1,x_2,x_3,x_4\right)=\left(x_1\vee x_2\vee x_3\vee x_4\right)\wedge \left(x_1\vee x_2\vee x_3\vee \overline\right)\wedge \left(x_1\vee x_2\vee \overline\vee x_4\right)\wedge \left(x_1\vee \overline\vee x_3\vee \overline\right)\wedge \left(x_1\vee \overline\vee \overline\vee x_4\right)\wedge \left(\overline\vee x_2\vee x_3\vee \overline\right)\wedge \left(\overline\vee x_2\vee \overline\vee x_4\right)\wedge \left(\overline\vee x_2\vee \overline\vee \overline\right)\wedge \left(\overline\vee \overline\vee x_3\vee x_4\right)\wedge \left(\overline\vee \overline\vee x_3\vee \overline\right)\wedge \left(\overline\vee \overline\vee \overline\vee x_4\right)\wedge \left(\overline\vee \overline\vee \overline\vee \overline\right).\]

Источник

Совершенная нормальная форма — дизъюнктивная и конъюнктивная, правило построения

Что такое СДНФ

Нормальная форма логической формулы характеризуется тем, что для нее не свойственны эквивалентность, отрицание формул неэлементарного типа и знаки импликации.

Существует две формы нормального типа: КНФ (конъюнктивная нормальная форма) и ДНФ (дизъюнктивная нормальная форма).

СДНФ — совершенная дизъюнктивная нормальная форма формулы. СДНФ — способ написания функции алгебры логики в качестве логического выражения.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

СДНФ формулы — это равнозначная ей формула, которая представляет собой дизъюнкцию элементарных конъюнкций, при которых функция достигает показателя «1».

ДНФ выглядит следующим образом:

СДНФ обладает некоторыми определенными свойствами:

К СДНФ возможно привести любую формулу алгебры логики. Исключение составляет только тождественно ложная формула. СДНФ можно получить как используя таблицы истинности, так и через равносильные преобразования.

При построении таблицы истинности важно помнить, что логические переменные со значением «0» необходимо брать с отрицанием.

Что такое СКНФ

СКНФ — совершенная конъюнктивная нормальная форма. Формулу можно назвать таковой, когда она — конъюнкция неповторяющихся элементарных дизъюнкций.

Формула должна соответствовать нескольким условиям, чтобы называться СКНФ:

Правила построения по таблице истинности

Дизъюнктивная форма

Если функция равна 1, то для всех наборов переменных, при которых это происходит, записывается произведение. Однако переменные, которые имеют значение 0, берутся с отрицанием.

Конъюнктивная форма

Когда функция равна 0, то для всех наборов переменных, при которых это происходит, записывается сумма. Однако переменные, которые имеют значение 1, берутся с отрицанием.

Алгоритм приведения к СДНФ и СКНФ

Рассмотрим логическую функцию в виде таблицы истинности.

Алгоритм построения СДНФ по таблице истинности выглядит следующим образом:

Построим совершенную ДНФ:

И как результат получим следующую СДНФ:

Алгоритм построения СКНФ по таблице истинности выглядит следующим образом:

Построим совершенную КНФ:

И как результат получим следующую СКНФ:

Рассмотрев алгоритмы построения СДНФ и СКНФ ясно, что в случае подавляющей части наборов значений переменных функция равна 0, то значительно легче построить и СДНФ для получения ее формулы, а в обратном случае — СКНФ.

Доказательство эквивалентности

Доказать эквивалентность формул можно двумя способами.

Далее следуют примеры с некоторыми эквивалентными преобразованием в булевой алгебре и новыми эквивалентностями, которые возможно получить с их помощью.

Поглощение

Склеивание

Обобщенное склеивание

\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\)

\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\;\vee\;xyz\;\vee\;xy\overline z\;=\;xz\;\vee\;y\overline z\)

Расщепление

\(x\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;xy\;\vee\;\overline xy\;=\;x\;\cdot\;l\;\;\vee\;y\;\cdot\;l\;=\;x\;\vee\;y\)

Примеры с решением

Задача №1

Через применение закона де Моргана и правила \( x\;\rightarrow\;y\;=\;\overline x\;\vee\;y\) упростим выражения:

\(F\;=\;((((A\;\rightarrow\;B)\;\rightarrow\;\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;(((\overline A\;\vee\;B)\;\rightarrow\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\overline C\;)\;=\)

\(=\;((((\overline A\;\vee\;B)\;\rightarrow\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;((\overline<((\overline A\;\vee\;B)>\;\vee\;\overline A)\;\rightarrow\overline B)\;\rightarrow\overline C)\;=\)

\(=(((\overline A\;\vee\;B)\;\vee\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\;\overline C)\;=((\overline<(\overline<(\overline A\vee B)>\;\vee\;\overline A\;)>\;\vee\;\overline B)\;\rightarrow\;\overline C)\;=\)

\(=\;((\overline<(\overline A\;\vee\;B)>\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge B)\;\vee\;\overline C\;=\)

\(=((A\overline B\;\vee\;\overline A)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\)

\(=\;((A\overline B\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(A\overline BB\;\vee\;\overline AB)\;\vee\;\overline C\;=\;(0\;\vee\;\overline AB)\;\vee\;\overline C\;=\;\overline AB\;\vee\;\overline C\)

Далее приведем выражение к КНФ:

\(F\;=\;\overline AB\;\vee\;\overline C\;\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\)

Далее приведем выражение к СКНФ:

\(F\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\;=\;(\overline A\;\vee\:\overline C\;\vee\;B\overline B)\;\wedge\;(A\overline A\;\vee\;B\;v\;\overline C)\;=\)

\(=\;(\overline A\;\vee\;\overline C\;\vee\;B)\;\wedge\;(A\;\vee\;B\;\vee\;\overline C)\;\wedge\;(\overline A\;\vee\;\overline C\;\vee\;\overline B)\;\wedge\;(\overline A\;\vee\;B\;\;\overline C)\)

Задача №2

Используя эквивалентные преобразования, постройте ДНФ функции \(f(\widetilde x^n)\)

\(f(\widetilde x^3) = (\overlinex_2\;\oplus\;x_3)\;\cdot\;(x_1x_3\;\rightarrow\;x_2)\)

\(f(\widetilde x^3) = (\overlinex_2\;\oplus\;x_3)\;\cdot\;(x_1x_3\;\rightarrow\;x_2) = ((\overlinex_2\;\cdot\;\overline\;)\;\vee\;(\overline<\overlinex_2>\;\cdot\;x_3))\;\cdot\;(\overline\;\vee\;x_2)\;=\)

\(=(\overlinex_2\overline\;\cdot(x_1\vee x_3\vee x_2)\;\vee\;x_1x_3\;\cdot\;(\overline\;\vee\;\overline\;\vee\;x_2)\;\vee\;\overlinex_3\;\cdot\;(\overline\;\vee\;\overline\;\vee\;x_2))\;=\)

Источник

Для всякой логической формулы с помощью тождественных преобразований можно построить бесконечно много равносильных ей формул. В алгебре логики одной из основных задач является поиск канонических форм (т. е. формул, построенных по единому правилу, канону).

Если логическая функция выражена через дизъюнкцию, конъюнкцию и отрицание переменных, то такая форма представления называется нормальной.

Среди нормальных форм выделяются совершенные нормальные формы (такие формы, в которых функции записываются единственным образом).

Совершенная дизъюнктивная нормальная форма (СДНФ)

Определение. Формулу называют элементарной конъюнкцией, если она образованна конъюнкцией некоторого числа переменных или их отрицаний.

Определение. Формула называтся дизъюнктивной нормальной формой (ДНФ), если она является дизъюнкцией неповторяющихся элементарных конъюнкций.

Определение. Логическая формула от k переменных называется совершенной дизъюнктивной нормальной формой (СДНФ), если:
1) формула является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция k переменных х₁, х₂, …, х_k, причем на i-м месте этой конъюнкции стоит либо переменная х_i, либо ее отрицание;
2) все элементарные конъюнкции в такой ДНФ попарно различны.

Совершенная конъюнктивная нормальная форма (СКНФ)

Определение. Формулу называют элементарной дизъюнкцией, если она образована дизъюнкцией некоторого числа переменных или их отрицаний.

Определение. Формула называется конъюнктивной нормальной формой (КНФ), если она является конъюнкцией неповторяющихся элементарных дизъюнкций.

Определение. Логическая формула от k переменных называется совершенной конъюнктивной нормальной формой (КДНФ), если:
1) формула является КНФ, в которой каждая элементарная дизъюнкция есть дизъюнкция k переменных х₁, х₂, …, х_k, причем на i-м месте этой дизъюнкции стоит либо переменная х_i, либо ее отрицание;
2) все элементарные дизъюнкции в такой КНФ попарно различны.

Алгоритм построения СДНФ по таблице истинности

Алгоритм построения СКНФ по таблице истинности

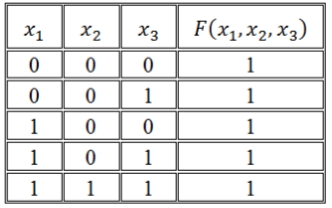
Пример: Дана таблица истинности логической функции от трех переменных. Построить логическую формулу, реализующую эту функцию.

x	y	z	F (x, y, z)
0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	1

Т.к. на большинстве строк таблицы истинности значение функции равно 1, то построим СКНФ. В результате получим следующую логическую формулу:
F = (¬ x ∨ y ∨ z) ∧ (¬ x ∨ y ∨ ¬ z)

Проверим полученную формулу. Для этого построим таблицу истинности функции.

x	y	z	¬ x	¬ x ∨ y ∨ z	¬ z	¬ x ∨ y ∨ ¬ z	F (x, y, z)
0	0	0	1	1	1	1	1
0	0	1	1	1	0	1	1
0	1	0	1	1	1	1	1
0	1	1	1	1	0	1	1
1	0	0	0	0	1	1	0
1	0	1	0	1	0	0	0
1	1	0	0	1	1	1	1
1	1	1	0	1	0	1	1

Сравнив исходную таблицу истинности и построенную для логической формулы, заметим, что столбцы значений функции совпадают. Значит, логическая функция построена верно.

Источник

Сайт aromolux.ru

Что такое совершенная конъюнктивная нормальная форма

Что такое совершенная конъюнктивная нормальная форма

СКНФ [ править ]

Алгоритм построения СКНФ по таблице истинности [ править ]

Пример построения СКНФ для медианы [ править ]

Построение СКНФ для медианы от трех аргументов [ править ]

Построение СКНФ для медианы от пяти аргументов [ править ]

Примеры СКНФ для некоторых функций [ править ]

Построение СКНФ и СДНФ по таблице истинности

Правила построения СКНФ по таблице истинности

Правила построения СДНФ по таблице истинности