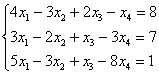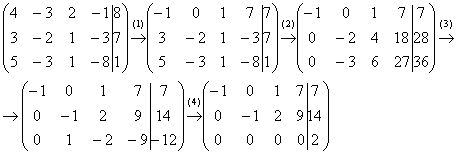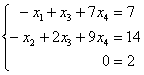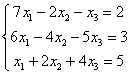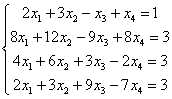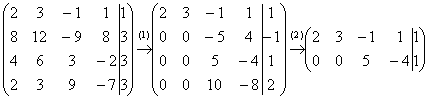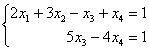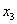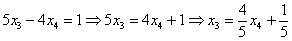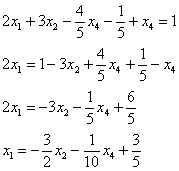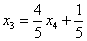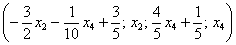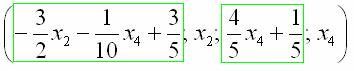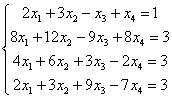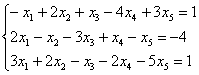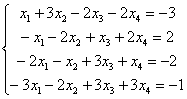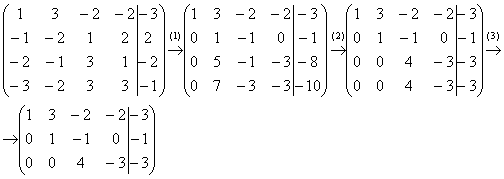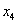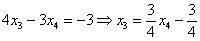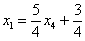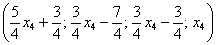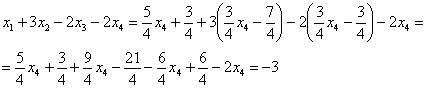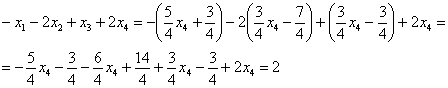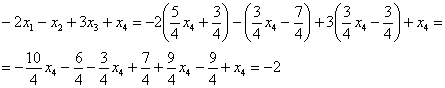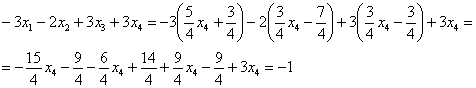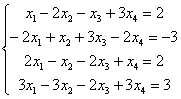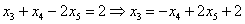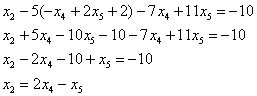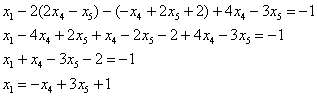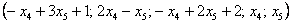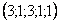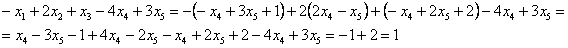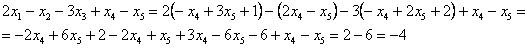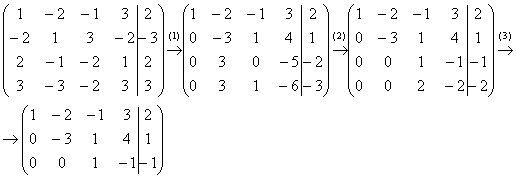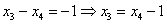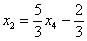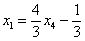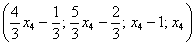Что такое совместность матрицы

Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность. Первая часть.

Исследовать систему линейных агебраических уравнений (СЛАУ) на совместность означает выяснить, есть у этой системы решения, или же их нет. Ну и если решения есть, то указать сколько их.

Следствие из теоремы Кронекера-Капелли

Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения или нет, а если существуют – то сколько.

Способ №1. Вычисление рангов по определению.

Подводя итог сказанному, отмечу, что первый способ хорош для тех СЛАУ, у которых матрица системы квадратна. При этом сама СЛАУ содержит три или четыре неизвестных и взята из стандартных типовых расчетов или контрольных работ.

Способ №2. Вычисление ранга методом элементарных преобразований.

Какие преимущества второго способа? Главное преимущество – это его универсальность. Нам совершенно неважно, является ли матрица системы квадратной или нет. Кроме того, мы фактически провели преобразования прямого хода метода Гаусса. Осталось лишь пару действий, и мы смогли бы получить решение данной СЛАУ. Честно говоря, второй способ нравится мне более первого, но выбор – это дело вкуса.

Ответ: Заданная СЛАУ совместна и определена.

Ответ: система несовместна.

Приводим расширенную матрицу системы к ступенчатому виду:

Ответ: система является неопределённой.

Во второй части мы разберём примеры, которые нередко включают в типовые расчёты или контрольные работы по высшей математике: исследование на совместность и решение СЛАУ в зависимости от значений параметров, входящих в неё.

Источник

Условие совместности системы линейных уравнений. Теорема Кронекера-Капелли

Установить, совместна ли система линейных уравнений, с помощью теоремы Кронекера-Капелли часто можно быстрее, чем с помощью метода Гаусса, когда требуется последовательно исключать неизвестные. Основана эта теорема на использовании ранга матрицы.

Ранги этих матриц связаны неравенством , при этом ранг матрицы В может быть лишь на одну единицу больше ранга матрицы A.

Следствие из теоремы Кронекера-Капелли о числе решений. Пусть для системы m линейных уравнений с n неизвестными выполнено условие совместности, то есть ранг матрицы из коэффициентов системы равен рангу её расширенной матрицы. Тогда верно следующее.

Если ранг матрицы системы линейных уравнений равен числу уравнений, то есть , то система совместна при любых свободных членах. В этом случае ранг расширенной матрицы также равен m, так как ранг матрицы не может быть больше числа её строчек.

В ходе доказательства теоремы Кронекера-Капелли были получены явные формулы для решений системы (в случае её совместности). Если уже известно, что система совместна, то, чтобы найти её решения, необходимо:

1) отыскать в матрице системы A ранга отличный от нуля минор порядка, равного рангу матрицы системы, то есть ранга r;

2) отбросить те уравнения, которые соответствуют строкам матрицы A, не входящим в минор ;

3) члены с коэффициентами, не входящими в , перенести в правую часть, а затем, придавая неизвестным, находящимся в правой части, произвольные значения, определить по формулам Крамера оставшиеся r неизвестных из системы r уравнений с отличным от нуля определителем .

Пример 1. Следуя теореме Кронекера-Капелли, установить, совместна ли система уравнений

Если система совместна, то решить её.

Решение. Вычисляем ранг матрицы этой системы и ранг расширенной матрицы. В обоих случаях он равен 3. Следовательно, система линейных уравнений совместна. Так как ранг матрицы системы меньше числа неизвестных, то система имеет бесконечно много решений: одно неизвестное может быть взято произвольно. Минор

отличен от нуля, поэтому последнее уравнение отбрасываем и неизвестному придаём произвольное значение .

Оставшиеся неизвестные определяются из системы

Решая последнюю систему по формулам Крамера или иным способом, находим

,

,

.

Присоединяя сюда , получаем все решения данной системы линейных уравнений.

Пример 2. Следуя теореме Кронекера-Капелли, установить, совместна ли система уравнений

Если система совместна, то решить её.

Решение. Вычисляем ранг матрицы этой системы:

.

Следовательно, ранг системы равен 3. Определим ранг расширенной матрицы:

.

Это означает, что ранг расширенной матрицы также равен 3. Следовательно, система совместна, а так как число неизвестных равно рангу матрицы системы, то она имеет единственное решение. Для решения можем использовать первые три уравнения:

Решая последнюю систему по формулам Крамера, находим

,

,

.

Источник

Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами

Содержание:

Методы решения систем линейных алгебраических уравнений (СЛАУ)

Метод Крамера

Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение

Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы

Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на для этого умножим все элементы первого столбца на эту неизвестную:

Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.

Определение: Определитель называется первым вспомогательным определителем СЛАУ.

Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:

31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.

Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины Проанализируем полученные формулы:

Пример:

Решить СЛАУ методом Крамера

Решение:

Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом

Найдем главный определитель СЛАУ (раскрываем по первой строке)

Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя

Воспользуемся формулами Крамера

Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.

Выполним проверку Отсюда видно, что СЛАУ решена верно.

Матричный способ решения СЛАУ

Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных матpицы-столбцы неизвестных и свободных коэффициентов

Тогда СЛАУ можно записать в матричном виде Матричный способ решения СЛАУ состоит в следующем: умножим слева матричное уравнение на обратную матрицу к матрице А, получим в силу того, что произведение найдем Таким образом, для нахождения неизвестных матричным способом, надо найти обратную к А матрицу после чего надо умножить эту матрицу на матрицу-столбец свободных коэффициентов.

Пример:

Решить СЛАУ матричным способом

Решение:

Введем в рассмотрение следующие матрицы

Найдем матрицу (см. Лекцию № 2): найдем детерминант матрицы А.

Пример:

Решение:

Найдем алгебраические дополнения всех элементов Запишем обратную матрицу (в правильности нахождения обратной матрицы убедиться самостоятельно). Подействуем пай денной матрицей на матрицу-столбец свободных коэффициентов В:

Отсюда находим, что х = 1; y = l; z = l.

Метод Гаусса

Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:

Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.

Обменяем в расширенной матрице первую и вторую строки местами, получим Приведем матрицу к треугольному виду, выполнив следующие преобразования: умножим элементы первой строки на (-2) и прибавим к соответствующим элементам второй строки Разделим все элементы второй строки на (-5), получим эквивалентную матрицу

Из первого уравнения находим, что х = 1.

Вывод: Из вышеизложенного материала следует, что вне зависимости от

способа решения СЛАУ всегда должен получаться один и тот же ответ.

Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.

Ранг матрицы. Теорема Кронекера-Капелли

Определение: Рангом матрицы называется наивысший порядок отличного от нуля минора этой матрицы.

Если то среди всевозможных миноров этой матрицы есть хотя бы один минор порядка r, который отличен от нулю, а все миноры порядков больших, чем r, равны нулю.

При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.

Пример:

Найти ранг матрицы

Решение:

Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, среди миноров третьего порядка также есть миноры, которые не равны нулю, например, Очевидно, что определитель четвертого порядка равен нулю, так как он будет содержать строку, состоящую из одних нулей (см. свойство для определителей). Следовательно, ранг матрицы А равен 3.

Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.

Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).

Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).

В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Общая теория систем линейных уравнений

Условия совместности.

Займемся изучением систем из m уравнений с n неизвестными. Систему
\begina_<1>^<1>x^<1>+a_<2>^<1>x^<2>+. +a_^<1>x^=b^<1>,\\a_<1>^<2>x^<1>+a_<2>^<2>x^<2>+. +a_^<2>x^=b^<2>,\\\cdots\\a_<1>^x^<1>+a_<2>^x^<2>+. +a_^x^=b^\end мы можем кратко записать в виде \tag <1>A\boldsymbol=\boldsymbol.
Система задается своей расширенной матрицей A^ <*>, получаемой объединением матрицы системы A и столбца свободных членов \boldsymbol .

Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

Иначе это утверждение можно сформулировать так.

Система линейных уравнений несовместна тогда и только тогда, когда противоречивое равенство 0=1 является линейной комбинацией ее уравнений.

Равенство рангов матрицы системы и расширенной матрицы можно выразить, понимая ранг матрицы как строчный ранг. Это приведет нас к важной теореме, известной как теорема Фредгольма.

Для того чтобы система (1) была совместна, необходимо и достаточно, чтобы каждое решение сопряженной однородной системы (3) удовлетворяло уравнению \tag <4>\boldsymbol^\boldsymbol=y_<1>b^<1>+. +y_b^=0.

Нахождение решений.

Для удобства записи будем предполагать, что первые r столбцов — базисные. Тогда преобразованную систему можно записать в виде \tag <5>\begin x^<1>=\beta^<1>-(\alpha_^<1>x^+. +\alpha_^<1>x^),\\\cdots\\x^=\beta^-(\alpha_^x^+. +\alpha_^x^).\end
Здесь \alpha_^ и \beta^ — элементы преобразованной расширенной матрицы. В левых частях равенств мы оставили неизвестные, соответствующие выбранным нами базисным столбцам, так называемые базисные неизвестные. Остальные неизвестные, называемые параметрическими, перенесены в правые части равенств.

На формулах (5) можно было бы и остановиться, но ниже мы дадим более простое и наглядное, а также принципиально важное описание совокупности решений системы линейных уравнений.

Приведенная система.

Сопоставим системе линейных уравнений (1) однородную систему с той же матрицей коэффициентов: \tag<6>A\boldsymbol=\boldsymbol. По отношению к системе (1) она называется приведенной.

Это предложение сводит задачу описания множества решений совместной системы линейных уравнений к описанию множества решений ее приведенной системы.

Однородная система совместна. Действительно, нулевой столбец является ее решением. Это решение называется тривиальным.

Если \boldsymbol_ <1>и \boldsymbol_ <2>— решения однородной системы, то любая их линейная комбинация — также решение этой системы.

Действительно, из A\boldsymbol_<1>=\boldsymbol и A\boldsymbol_<2>=\boldsymbol для любых \alpha и \beta следует A(\alpha \boldsymbol_<1>+\beta \boldsymbol_<2>)=\alpha A \boldsymbol_<1>+\beta A\boldsymbol_<2>=\boldsymbol .

Если однородная система имеет нетривиальные решения, то можно указать несколько линейно независимых решений таких, что любое решение является их линейной комбинацией. Сделаем это.

Столбцы фундаментальной матрицы называются фундаментальной системой решений.

Ниже мы докажем, что в остальных случаях фундаментальная матрица существует, но сначала выясним, что означает третье условие в определении.

Таким образом, мы получили

Итак, система столбцов (8) — фундаментальная система решений. Она называется нормальной фундаментальной системой решений. Каждому выбору базисных столбцов соответствует своя нормальная фундаментальная система решений. Вообще же, каждая система из n-r линейно независимых решений является фундаментальной.

Для нахождения матрицы (8) можно привести матрицу A системы к упрощенному виду, что даст коэффициенты разложения небазисных столбцов по базисным.

Столбец \boldsymbol — решение системы A\boldsymbol=\boldsymbol тогда и только тогда, когда существует такой столбец \boldsymbol , что \tag <9>\boldsymbol=F\boldsymbol.

Общее решение системы линейных уравнений.

Теперь мы можем собрать воедино наши результаты — утверждения 2 и 6.

Одна из ранее доказанных нами теорем гласит, что для существования единственного решения системы из n линейных уравнений с n неизвестными достаточно, чтобы матрица системы имела детерминант, отличный от нуля. Сейчас легко получить и необходимость этого условия.

Равенство \det A=0 означает, что \mathbf\,A и, следовательно, приведенная система имеет бесконечно много решений. Если данная система совместна, то из теоремы 3 следует, что и она имеет бесконечно много решений.

Пример.

Источник

Решение систем линейных уравнений. Несовместные системы.
Системы с общим решением. Частные решения

Продолжаем разбираться с системами линейных уравнений. До сих пор я рассматривал системы, которые совместны и имеют единственное решение. Такие системы можно решить любым способом: методом подстановки («школьным»), по формулам Крамера, матричным методом, методом Гаусса. Однако на практике широко распространены еще два случая:

– Система несовместна (не имеет решений);
– Система совместна и имеет бесконечно много решений.

Примечание: термин «совместность» подразумевает, что у системы существует хоть какое-то решение. В ряде задач требуется предварительно исследовать систему на совместность, как это сделать – см. статью о ранге матриц.

Для этих систем применяют наиболее универсальный из всех способов решения – метод Гаусса. На самом деле, к ответу приведет и «школьный» способ, но в высшей математике принято использовать гауссовский метод последовательного исключения неизвестных. Те, кто не знаком с алгоритмом метода Гаусса, пожалуйста, сначала изучите урок метод Гаусса для чайников.

Сами элементарные преобразования матрицы – точно такие же, разница будет в концовке решения. Сначала рассмотрим пару примеров, когда система не имеет решений (несовместна).

Решить систему линейных уравнений

Что сразу бросается в глаза в этой системе? Количество уравнений – меньше, чем количество переменных. Если количество уравнений меньше, чем количество переменных, то сразу можно сказать, что система либо несовместна, либо имеет бесконечно много решений. И это осталось только выяснить.

Начало решения совершенно обычное – запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

(1) На левой верхней ступеньке нам нужно получить +1 или –1. Таких чисел в первом столбце нет, поэтому перестановка строк ничего не даст. Единицу придется организовать самостоятельно, и сделать это можно несколькими способами. Я поступил так: К первой строке прибавляем третью строку, умноженную на –1.

(2) Теперь получаем два нуля в первом столбце. Ко второй строке прибавляем первую строку, умноженную на 3. К третьей строке прибавляем первую строку, умноженную на 5.

(3) После выполненного преобразования всегда целесообразно посмотреть, а нельзя ли упростить полученные строки? Можно. Вторую строку делим на 2, заодно получая нужную –1 на второй ступеньке. Третью строку делим на –3.

(4) К третьей строке прибавляем вторую строку.

Наверное, все обратили внимание на нехорошую строку, которая получилась в результате элементарных преобразований: . Ясно, что так быть не может. Действительно, перепишем полученную матрицу обратно в систему линейных уравнений:

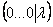
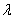
Если в результате элементарных преобразований получена строка вида , где – число, отличное от нуля, то система несовместна (не имеет решений).

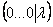
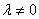
Как записать концовку задания? Нарисуем белым мелом: «в результате элементарных преобразований получена строка вида , где » и дадим ответ: система не имеет решений (несовместна).

Если же по условию требуется ИССЛЕДОВАТЬ систему на совместность, тогда необходимо оформить решение в более солидном стиле с привлечением понятия ранга матрицы и теоремы Кронекера-Капелли.

Обратите внимание, что здесь нет никакого обратного хода алгоритма Гаусса – решений нет и находить попросту нечего.

Решить систему линейных уравнений

Это пример для самостоятельного решения. Полное решение и ответ в конце урока. Снова напоминаю, что ваш ход решения может отличаться от моего хода решения, у алгоритма Гаусса нет сильной «жёсткости».

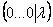
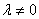
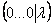
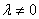
Еще одна техническая особенность решения: элементарные преобразования можно прекращать сразу же, как только появилась строка вида , где . Рассмотрим условный пример: предположим, что после первого же преобразования получилась матрица . Матрица еще не приведена к ступенчатому виду, но в дальнейших элементарных преобразованиях нет никакой необходимости, так как появилась строка вида , где . Следует сразу дать ответ, что система несовместна.

Когда система линейных уравнений не имеет решений – это почти подарок, ввиду того, что получается короткое решение, иногда буквально в 2-3 действия.

Но всё в этом мире уравновешено, и задача, в которой система имеет бесконечно много решений – как раз длиннее.

Решить систему линейных уравнений

Тут 4 уравнений и 4 неизвестных, таким образом, система может иметь либо единственное решение, либо не иметь решений, либо иметь бесконечно много решений. Как бы там ни было, но метод Гаусса в любом случае приведет нас к ответу. В этом его и универсальность.

Начало опять стандартное. Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Вот и всё, а вы боялись.

(1) Обратите внимание, что все числа в первом столбце делятся на 2, поэтому на левой верхней ступеньке нас устраивает и двойка. Ко второй строке прибавляем первую строку, умноженную на –4. К третьей строке прибавляем первую строку, умноженную на –2. К четвертой строке прибавляем первую строку, умноженную на –1.

Внимание! У многих может возникнуть соблазн из четвертой строки вычесть первую строку. Так делать можно, но не нужно, опыт показывает, что вероятность ошибки в вычислениях увеличивается в несколько раз. Только складываем: К четвертой строке прибавляем первую строку, умноженную на –1 – именно так!

(2) Последние три строки пропорциональны, две из них можно удалить.

Здесь опять нужно проявить повышенное внимание, а действительно ли строки пропорциональны? Для перестраховки (особенно, чайнику) не лишним будет вторую строку умножить на –1, а четвертую строку разделить на 2, получив в результате три одинаковые строки. И только после этого удалить две из них.

В результате элементарных преобразований расширенная матрица системы приведена к ступенчатому виду: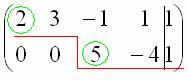

При оформлении задачи в тетради желательно для наглядности делать такие же пометки карандашом.

Перепишем соответствующую систему уравнений:

«Обычным» единственным решением системы здесь и не пахнет. Нехорошей строки 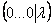тоже нет. Значит, это третий оставшийся случай – система имеет бесконечно много решений. Иногда по условию нужно исследовать совместность системы (т.е. доказать, что решение вообще существует), об этом можно прочитать в последнем параграфе статьи Как найти ранг матрицы? Но пока разбираем азы:

Бесконечное множество решений системы коротко записывают в виде так называемого общего решения системы.

Общее решение системы найдем с помощью обратного хода метода Гаусса.

Сначала нужно определить, какие переменные у нас являются базисными, а какие переменные свободными. Не обязательно заморачиваться терминами линейной алгебры, достаточно запомнить, что вот существуют такие базисные переменные и свободные переменные.

Базисные переменные всегда «сидят» строго на ступеньках матрицы.
В данном примере базисными переменными являются 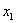и

Свободные переменные – это все оставшиеся переменные, которым не досталось ступеньки. В нашем случае их две: 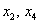– свободные переменные.

Теперь нужно все базисные переменные выразить только через свободные переменные.

Обратный ход алгоритма Гаусса традиционно работает снизу вверх.
Из второго уравнения системы выражаем базисную переменную :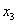

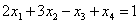
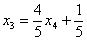
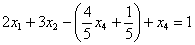
Теперь смотрим на первое уравнение: . Сначала в него подставляем найденное выражение :

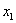
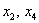
Осталось выразить базисную переменную через свободные переменные :

В итоге получилось то, что нужно – все базисные переменные ( и ) выражены только через свободные переменные :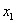

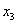
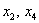
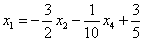
Собственно, общее решение готово:

Как правильно записать общее решение?
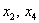
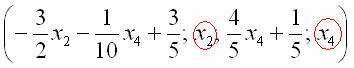
Свободные переменные записываются в общее решение «сами по себе» и строго на своих местах. В данном случае свободные переменные следует записать на второй и четвертой позиции:
.

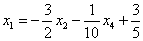
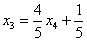
Полученные же выражения для базисных переменных и , очевидно, нужно записать на первой и третьей позиции:

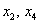
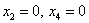
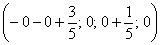
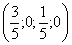
Придавая свободным переменным произвольные значения, можно найти бесконечно много частных решений. Самыми популярными значениями являются нули, поскольку частное решение получается проще всего. Подставим в общее решение:

– частное решение.

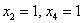
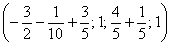
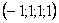
Другой сладкой парочкой являются единицы, подставим в общее решение:

– еще одно частное решение.

Легко заметить, что система уравнений имеет бесконечно много решений (так как свободным переменным мы можем придать любые значения)

Каждое частное решение должно удовлетворять каждому уравнению системы. На этом основана «быстрая» проверка правильности решения. Возьмите, например, частное решение 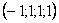и подставьте его в левую часть каждого уравнения исходной системы:

Всё должно сойтись. И с любым полученным вами частным решением – тоже всё должно сойтись.

Но, строго говоря, проверка частного решения иногда обманывает, т.е. какое-нибудь частное решение может удовлетворять каждому уравнению системы, а само общее решение на самом деле найдено неверно.

Поэтому более основательна и надёжна проверка общего решения. Как проверить полученное общее решение ?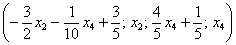

Это несложно, но довольно муторно. Нужно взять выражения базисных переменных, в данном случае и , и подставить их в левую часть каждого уравнения системы.

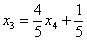
В левую часть первого уравнения системы: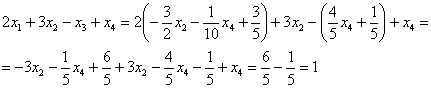

Получена правая часть исходного уравнения.

В левую часть второго уравнения системы: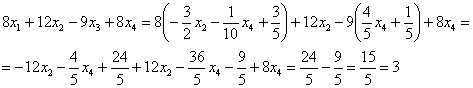

Получена правая часть исходного уравнения.

И далее – в левые части третьего и четвертого уравнение системы. Это дольше, но зато гарантирует стопроцентную правильность общего решения. Кроме того, в некоторых заданиях требуют проверку общего решения.

Решить систему методом Гаусса. Найти общее решение и два частных. Сделать проверку общего решения.

Это пример для самостоятельного решения. Здесь, кстати, снова количество уравнений меньше, чем количество неизвестных, а значит, сразу понятно, что система будет либо несовместной, либо с бесконечным множеством решений. Что важно в самом процессе решения? Внимание, и еще раз внимание. Полное решение и ответ в конце урока.

И еще пара примеров для закрепления материала

Решить систему линейных уравнений. Если система имеет бесконечно много решений, найти два частных решения и сделать проверку общего решения

Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

(1) Ко второй строке прибавляем первую строку. К третьей строке прибавляем первую строку, умноженную на 2. К четвертой строке прибавляем первую строку, умноженную на 3.
(2) К третьей строке прибавляем вторую строку, умноженную на –5. К четвертой строке прибавляем вторую строку, умноженную на –7.
(3) Третья и четвертая строки одинаковы, одну из них удаляем.

Вот такая красота: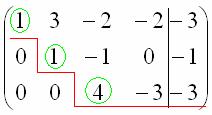

Базисные переменные сидят на ступеньках, поэтому 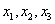– базисные переменные.
Свободная переменная, которой не досталось ступеньки здесь всего одна:

Обратный ход:
Выразим базисные переменные через свободную переменную:
Из третьего уравнения:

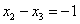
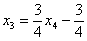
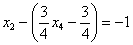
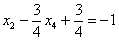
Рассмотрим второе уравнение и подставим в него найденное выражение :

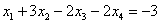
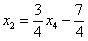
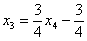
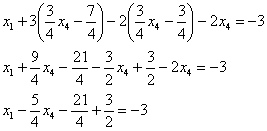
Рассмотрим первое уравнение и подставим в него найденные выражения и :

Таким образом, общее решение:

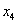
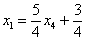
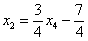
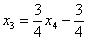
Еще раз, как оно получилось? Свободная переменная одиноко сидит на своём законном четвертом месте. Полученные выражения для базисных переменных , тоже заняли свои порядковые места.

Сразу выполним проверку общего решения. Работа для негров, но она у меня уже выполнена, поэтому ловите =)

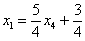
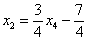
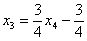
Подставляем трех богатырей , , в левую часть каждого уравнения системы:

Получены соответствующие правые части уравнений, таким образом, общее решение найдено верно.

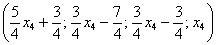
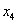
Теперь из найденного общего решения получим два частных решения. Шеф-поваром здесь выступает единственная свободная переменная . Ломать голову не нужно.

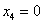
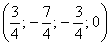
Пусть , тогда – частное решение.
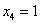
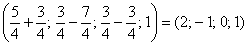
Пусть , тогда – еще одно частное решение.

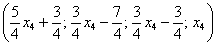
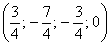
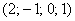
Ответ: Общее решение: , частные решения: , .

Много математики вредно, поэтому похожий заключительный пример для самостоятельного решения.

Найти общее решение системы линейных уравнений.

Проверка общего решения у меня уже сделана, ответу можно доверять. Ваш ход решения может отличаться от моего хода решения, главное, чтобы совпали общие решения.

Наверное, многие заметили неприятный момент в решениях: очень часто при обратном ходе метода Гаусса нам пришлось возиться с обыкновенными дробями. На практике это действительно так, случаи, когда дробей нет – встречаются значительно реже. Будьте готовы морально, и, самое главное, технически.

Остановлюсь на некоторых особенностях решения, которые не встретились в прорешанных примерах.

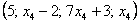
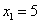
В общее решение системы иногда может входить константа (или константы), например: . Здесь одна из базисных переменных равна постоянному числу: . В этом нет ничего экзотического, так бывает. Очевидно, что в данном случае любое частное решение будет содержать пятерку на первой позиции.

Редко, но встречаются системы, в которых количество уравнений больше количества переменных. Метод Гаусса работает в самых суровых условиях, следует невозмутимо привести расширенную матрицу системы к ступенчатому виду по стандартному алгоритму. Такая система может быть несовместной, может иметь бесконечно много решений, и, как ни странно, может иметь единственное решение.

И, конечно, повторюсь в своем совете – чтобы комфортно себя чувствовать при решении системы методом Гаусса, следует набить руку и прорешать хотя бы десяток систем.

Пример 2: Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.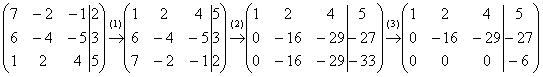

Выполненные элементарные преобразования:
(1) Первую и третью строки поменяли местами.
(2) Ко второй строке прибавили первую строку, умноженную на –6. К третьей строке прибавили первую строку, умноженную на –7.
(3) К третьей строке прибавили вторую строку, умноженную на –1.
В результате элементарных преобразований получена строка вида 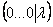, где , значит, система несовместна.
Ответ: решений нет.

Пример 4: Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду: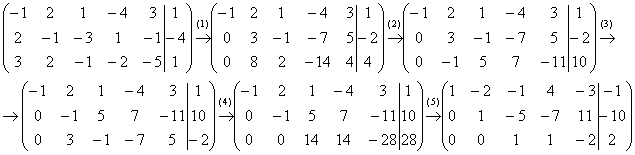

Выполненные преобразования:
(1) Ко второй строке прибавили первую строку, умноженную на 2. К третьей строке прибавили первую строку, умноженную на 3.

Для второй ступеньке нет единицы, и преобразование (2) направлено на её получение.

(2) К третьей строке прибавили вторую строку, умноженную на –3.
(3) Вторую с третью строки поменяли местами (переставили полученную –1 на вторую ступеньку)
(4) К третьей строке прибавили вторую строку, умноженную на 3.
(5)У первых двух строк сменили знак (умножили на –1), третью строку разделили на 14.

Обратный ход.
– базисные переменные (те, которые на ступеньках), – свободные переменные (те, кому не досталось ступеньки).

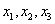
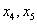
Выразим базисные переменные через свободные переменные:
Из третьего уравнения:

Рассмотрим второе уравнение: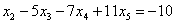
Подставим в него найденное выражение :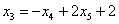

Рассмотрим первое уравнение: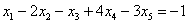
Подставим в него найденные выражения: , :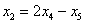

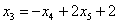
Общее решение:

Найдем два частных решения
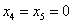
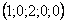
Если , то
Если 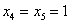, то

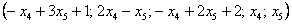
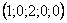
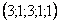
Ответ: Общее решение: , частные решения: , .

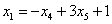
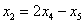
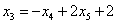
Проверка: подставим найденное решение (выражения базисных переменных , и ) в левую часть каждого уравнения системы:

Получены соответствующие правые части, таким образом, общее решение найдено верно.

Пример 6: Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

(1) Ко второй строке прибавляем первую строку, умноженную на 2. К третьей строке прибавляем первую строку, умноженную на –2. К четвертой строке прибавляем первую строку, умноженную на –3.
(2) К третьей строке прибавляем вторую строку. К четвертой строке прибавляем вторую строку.
(3) Третья и четвертая строки пропорциональны, одну из них удаляем.

– базисные переменные, – свободная переменная. Выразим базисные переменные через свободную переменную:

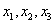
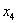
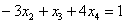
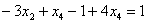
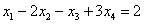
Ответ: Общее решение:

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник