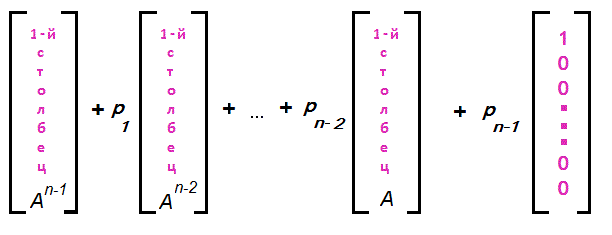Что такое спектр матрицы

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Характеристический полином, собственные числа, собственные векторы матрицы

Характеристический полином

Теорема 1.

Пример. Характеристический полином матрицы Фробениуса

Характеристический полином линейного оператора

определяется как характеристический полином матрицы этого оператора в произвольном базисе линейного пространства, в котором этот оператор задан. Подробнее ☞ ЗДЕСЬ.

Характеристический полином линейного однородного разностного уравнения

Свойства

Теорема 2. Характеристический полином матрицы не меняется

Теорема Гамильтона-Кэли

матрица является корнем своего характеристического полинома.

Доказательство ☞ ЗДЕСЬ.

Собственное число

Пример. Найти спектр матрицы

Доказательство следует из представления характеристического полинома через миноры матрицы и формул Виета. ♦

Имеет место следующее равенство:

Доказательство ☞ ЗДЕСЬ.

Доказательство ☞ ЗДЕСЬ.

Доказательство ☞ ЗДЕСЬ.

Теорема 11. Спектр циклической матрицы

Доказательство ☞ ЗДЕСЬ.

Локализация собственных чисел

Теорема 12. [1]. Собственные числа матрицы являются непрерывными функциями ее элементов. Иначе: пусть

Собственно факт непрерывной зависимости собственных чисел от элементов матрицы следует из представления характеристического полинома из теоремы ☞ ПУНКТА — коэффициенты этого полинома полиномиально (и, следовательно, непрерывно) зависят от элементов матрицы. Далее используем теорему о непрерывной зависимости корней полинома от его коэффициентов.

Выясним теперь на примере, насколько малым может быть возмущение элементов матрицы чтобы сохранились хотя бы количество вещественных корней ее характеристического полинома.

Пример [Уилкинсон] [2]. Найти собственные числа матрицы

Пример. Найти собственные векторы матрицы

Еще один способ нахождения собственного вектора основан на теореме Гамильтона-Кэли.

Пример. Найти собственные векторы матрицы

Пример. Вычислить собственный вектор матрицы

Пример. Найти представление всех собственных векторов матрицы

Доказательство ☞ ЗДЕСЬ.

Теорема Перрона-Фробениуса

Пример. Найти собственное число и вектор Перрона-Фробениуса для матрицы

Пример. Спектр неотрицательной матрицы

Методы вычисления характеристического полинома

А в качестве усугубляющего положение обстоятельства «на заднем плане» маячит проблема точности вычислений коэффициентов характеристического полинома — чувствительность его корней к возмущению его коэффициентов бывает весьма высокой.

Метод Леверье

Пример [Леверье]. Найти характеристический полином матрицы

Пример. Для приведенного выше примера находим собственные числа:

Теорема 21. Характеристический полином явно выражается через суммы Ньютона с помощью следующего представления:

Биографические заметки о Леверье ☞ ЗДЕСЬ.

Метод Крылова

Теорема 22. Определитель

Пример. Найти характеристический полином матрицы примера Леверье

Пример. Найти характеристический полином матрицы

Поиск всех собственных чисел

Существуют методы нахождения спектра матрицы, не требующие предварительного построения характеристического полинома.

QR-алгоритм

Частичная проблема собственных чисел

Теорема 25. Как правило, предел

Как правило, вектор

Пример. Для матрицы

Теперь обсудим исключительные случаи алгоритма.

Пример. Найти максимальное по модулю собственное число матрицы примера Леверье

Пример. Для матрицы

При выполнении условия предположения 2 имеет место равенство

Пример. Для матрицы

Задачи

Источники

[2]. Уилкинсон Дж.Х. Алгебраическая проблема собственных значений. М.Наука. 1970, с.93-94

[3]. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.ГИФМЛ. 1960

[4]. Хорн Р., Джонсон Ч. Матричный анализ. М.Мир.1989

Источник

СОДЕРЖАНИЕ

Матрицы

Ограниченные линейные операторы

Спектральный радиус затем определяется как верхняя грань величин элементов в спектре:

Графики

Это определение распространяется на случай бесконечных графов с ограниченными степенями вершин (т.е. существует некоторое вещественное число C такое, что степень каждой вершины графа меньше, чем C ). В этом случае для графа G определим:

Верхняя граница

Верхние оценки спектрального радиуса матрицы

Следующее предложение показывает простую, но полезную оценку сверху спектрального радиуса матрицы:

и поскольку v ≠ 0, имеем

Верхние оценки спектрального радиуса графа

Последовательность мощности

Теорема

Спектральный радиус тесно связан с поведением сходимости степенной последовательности матрицы; а именно, имеет место следующая теорема:

Доказательство теоремы

и, поскольку J блочно-диагональный,

Формула Гельфанда

Теорема

Следующая теорема дает спектральный радиус как предел нормы матрицы.

Доказательство

Для любого ε > 0 сначала построим следующие две матрицы:

Сначала применим предыдущую теорему к A ₊ :

который по определению

Следствия Гельфанда

Формула Гельфанда непосредственно приводит к оценке спектрального радиуса произведения конечного числа матриц, а именно, предполагая, что все они коммутируют, получаем

который по определению

где + означает приближение к пределу сверху.

Пример

Источник

Спектральные свойства матриц-операторов

При действии линейного оператора вектор-прообраз (х) переходит в вектор-образ (у): Аx = y. Иногда между этими двумя векторами наблюдается пропорциональность: y= ax,и операторное уравнение приобретает видАx = ax. Другими словами, некоторые векторы при действии на них определенного оператора просто умножаются на определенное число, или, говоря геометрическим языком, изменяют только свою длину, но не направление. Такие особые векторы называются собственными векторами данного оператора. Каждый оператор имеет индивидуальный набор собственных векторов, причем их число строго определено — оно равно размерности матрицы (числу строк или столбцов). Иногда несколько собственных векторов одного и того же оператора совпадают друг с другом (являются вырожденными).

Число, на которое умножается собственный вектор при действии оператора (a), называется собственным значением или собственным числом оператора. Каждому собственному вектору соответствует свое собственное значение. Иногда несколько собственных чисел являются одинаковыми (вырожденными). Полный набор собственных значений оператора называется его спектром.

Если некоторый вектор а является собственным для оператора Аи ему соответствует собственное число a, то любой вектор, пропорциональный данному (т.е. k • a,где k — любое число), также является собственным, причем ему соответствует то же самое собственное число. Другими словами, каждый собственный вектор существует в бесконечном числе экземпляров, отличающихся друг от друга длиной, но совпадающих по направлению. Можно сказать, что говоря о собственном векторе, мы всегда подразумеваем под этим некоторый луч (или одномерное подпространство, ось), характеризуемый направлением, но не имеющий какой-либо определенной длины. При действии оператора на этот луч, он никак не изменяется. Поэтому часто употребляют такие термины как инвариантное направление или инвариантное подпространство. В качестве представителя такого собственного луча (инвариантного подпространства) часто используют нормированный вектор этого луча. В этом случае понятие собственного вектора становится вполне определенным не только в отношении направления, но и в отношении длины.

Собственные векторы и собственные значения операторов имеют чрезвычайно широкое применение в физике и химии. Так, например, квантово-механические волновые функции, с помощью которых описываются состояния атомов и молекул, являются собственными векторами оператора Гамильтона, а энергии этих состояний — собственными числами того же самого оператора. Можно сказать, что решение практически любой квантово-механической задачи сводится к нахождению собственных векторов и собственных чисел некоторых линейных операторов.

Поэтому обратимся к рассмотрению методов решения этой задачи. Стандартная процедура нахождения собственных векторов и соответствующих им собственных значений основана на уравнении:

Аа = aа

где а — собственный вектор оператора А, а a — соответствующее ему собственное значение. (Это уравнение часто называют уравнением на собственные значения, оно часто встречается в квантовой механике; например, известное уравнение Шредингера НY= ЕY является его частным случаем — уравнением на собственные значения для оператора Гамильтона).

Выберем некоторый базис и запишем уравнение в координатном представлении. Вектор а запишется в виде столбца чисел-координат (a_i), а оператор А — в виде квадратной матрицы, состоящей из матричных элементов (А_ij):

Раскроем эту матрично-векторную запись, соблюдая известные правила умножения матрицы на вектор-столбец, и получим обычную систему линейных уравнений:

Приведя подобные члены, получим более простую систему уравнений, в которых все свободные члены равны нулю. Такие системы называются однородными и отличаются одной существенной особенностью: они совместны (имеют решение) только тогда, когда определитель системы равен нулю. В этом случае система имеет бесконечно много решений, пропорциональных друг другу. Если определитель системы не равен нулю, то решений нет совсем.:

Как известно, определитель системы уравнений состоит из коэффициентов при неизвестных, и в данном случае он будет иметь вид:

Видно, что матрица этого определителя отличается от матрицы оператора только тем, что во все диагональные элементы внесена одна и та же поправка в виде дополнительного слагаемого (–a). Раскроем определитель по известным правилам и приведем подобные члены. Тогда в результате получим алгебраическое уравнение n-й степени, относительно неизвестного a:

Это уравнение называется характеристическим уравнением оператора. Всякое уравнение n-й степени имеет n корней (не обязательно различных). Поэтому, решив характеристическое уравнение, найдем n его корней, которые и являются собственными числами оператора. Другими словами, спектр оператора состоит из корней его характеристического уравнения.

Если подставить первое собственное значение в систему уравнений, то эта система будет заведомо совместной и может быть легко решена.

Рассмотрим для иллюстрации численный пример. Пусть имеется оператор с матрицей:

Первый этап решения — составление характеристического уравнения. Запишем определитель матрицы и раскроем его по известным правилам:

Решив это уравнение найдем три корня: a₁ = 8 ; a₂ = –1 ; a₃ = –1, которые и являются собственными значениями нашего оператора, т.е. составляют его спектр. Заметим, что здесь мы имеем случай дважды вырожденного корня.

Перейдем к определению собственных векторов, неизвестные координаты которых обозначим как x, y, z. Запишем систему уравнений в общем виде:

(3 – a) х + 2 y + 4 z = 0

Подставим в эту систему первое собственное значение a₁ = 8.

– 5 х + 2 y + 4 z = 0

Вычтем из первого уравнения третье и получим: –9x = 9z или x = z. Подставим этот результат во второе уравнение: 4х – 8у = 0, из чего следует, что у = х/2. Теперь мы можем выразить все три координаты вектора через одну, например, через х: х = х, у = х/2, z = x. Следовательно, решение можно записать в виде вектор-столбца:

От общего множителя (х/2) можно отказаться совсем (так как все векторы, пропорциональные друг другу, являются представителями одного и того же собственного луча) и ограничиться тремя числами в векторных скобках.

Перейдем к вырожденному собственному значению a = –1. С этим значением система приобретет вид:

4 х + 2 y + 4 z = 0

Видно, что все три уравнения одинаковы и задают только одно соотношение между тремя неизвестными. Поэтому мы может произвольно выбрать два из них, а третье уже выразить через эти два.

Используя геометрическую аналогию, мы можем сказать, что уравнение вида 2x + 1y + 2z = 0 определяет некоторую плоскость (двумерное подпространство) в трехмерном пространстве. Любой вектор, лежащий на этой плоскости является решением нашей системы и, следовательно, будет собственным для нашего оператора. Таким образом, в случае вырожденных собственных значений мы получаем уже не одномерное собственное подпространство (луч), а собственное подпространство, размерность которого равна степени вырожденности собственного значения. Очевидно, что перечислять все векторы этого собственного двумерного подпространства нет необходимости — достаточно выбрать среди них два любые вектора и принять их за базис. Тогда все собственные векторы, соответствующие вырожденому собственному значению, могут быть выражены в виде линейной комбинации этих двух базисных векторов. Обычно в качестве базисных выбирают ортогональные друг другу векторы (т.е. такие, для которых скалярное произведение равно нулю).

Заметим, что первый базисный вектор можно выбрать произвольно. Положим, например, х = 0 и у = 1. Тогда z = –1/2. Второй базисный вектор должен удовлетворять как уравнению плоскости (2x + 1y + 2z = 0), так и условию ортогональности:

Решая совместно эти уравнения, получим: у = –2/5 х и z = –4/5 х. Таким образом, два базисных вектора, определяющих собственное двумерное подпространство будут иметь вид:

Любой вектор, построенный в виде линейной комбинации:

b = aа₂+ bа₃

будет собственным для нашего оператора, с собственным значением, равным –1, что легко проверить непосредственным действием оператора:

Аb = А(aа₂+ bа₃­) = А(aа₂) + А(bа₃) = aА(а₂) + bА(а₃) =

= a(–1)(а₂) + b(–1)(а₃) = (–1) (aа₂ + bа₃) = (–1)b

Отметим еще одно важное свойство собственных векторов: они всегда образуют некоторый базис того линейного пространства, в котором действует рассматриваемый оператор. Он называется собственным базисом данного оператора. В ряде случаев использование собственного базиса позволяет существенно упростить вычислительную часть задачи, поскольку операторные уравнения, записанные в собственном базисе оператора, выглядят особенно просто. Матрица оператора, выраженная по отношению к собственному базису, имеет квазидиагональный вид: по диагонали матрицы располагаются квадратные блоки меньшего размера, а все элементы вне этих блоков равны нулю. Каждому невырожденному собственному значению соответствует блок единичного размера (1´1), т.е. просто число, причем это число и является собственным. Дважды вырожденным собственным значениям соответствует блок (2´2) и т.д. Особенно просто выглядит матрица для случая, когда у оператора нет вырожденных собственных значений — она является диагональной, причем по диагонали расположены ее собственные значения.

Вопросы для самоконтроля

1. Дайте определение понятиям «симметрия», «операция симметрии» и «элемент симметрии».

2. Перечислите известные Вам разновидности симметрии.

3. Перечислите все пространственные операции симметрии.

4. Дайте определение точечной группы симметрии. ТГС состоит их операций или элементов симметрии?

5. Каким образом связаны между собой элементы ТГС?

6. Дайте определение понятия «класс эквивалентности». Являются ли такие классы перекрывающимися?

7. Дайте определение понятиям «тип симметрии», «характер», «таблица характеров».

8. Для каких целей можно использовать типы симметрии?

9. Сколько типов симметрии имеет та или иная ТГС?

10. Дайте определение понятиям «вектор» и «векторное пространство». Какие векторные пространства называются линейными?

11. Дайте определение операциям, которые можно выполнять с векторами: сложение, умножение на число, разложение по базису, скалярное умножение, возведение в квадрат.

12. Для каких целей используется координатное представление векторов? Сколько координатных представлений может иметь заданный вектор?

13. В чем различие между векторами-строками и векторами-столбцами?

14. В чем различие между действительными и комплексными векторами?

15. В каких случаях необходимо использовать функциональное представление векторов?

16. Дайте определение понятиям «бра-вектор» и «кет-вектор».

17. Приведите формулы для вычисления модуля вектора и угла между двумя векторами.

18. В чем различие между двумя векторами, а) принадлежащими одному лучу? б) не принадлежащими одному лучу?

19. Как производится нормировка вектора?

20. Дайте определение понятиям «матрица», «транспонированная матрица», «обратная матрица», «ортогональная матрица», «самосопряженная матрица», «унитарная матрица».

21. Дайте определение операциям, которые можно выполнять с матрицами: сложение, умножение на число, скалярное умножение, транспонирование, комплексное и эрмитово сопряжение.

22. Приведите алгоритмы вычисления определителя, перманента и следа матрицы.

23. Приведите алгоритм нахождения обратной матрицы.

24. Какие матрицы можно использовать в качестве линейных операторов?

25. В чем различие между матричным преобразованием вектора-строки и вектора-столбца?

26. Дайте определение понятиям «собственный вектор» и «собственное значение». Сколько собственных векторов и собственных значений может иметь матрица-оператор?

27. Приведите алгоритм нахождения спектра матрицы-оператора.

28. В каких областях физики и химии находят применение математические модели вектора, векторного пространства, матрицы, линейного оператора?

Типовые задачи

1. Для заданной молекулы перечислить все операции симметрии и изобразить графически расположение соответствующих им элементов симметрии.

2. Для заданного набора операций симметрии или ТГС привести несколько примеров молекул, обладающих указанной симметрией.

3. Пользуясь таблицами характеров ТГС (Приложение), отнести к определенным типам симметрии проекции векторов импульса (p_x, p_y, p_z) и момента импульса (L_x, L_y, L_z).

4. Для заданных векторов построить вектор — линейную комбинацию с указанными коэффициентами и нормировать его. Рассчитать углы между исходными векторами и их линейной комбинацией.

5. Осуществить преобразование заданного вектора в форме столбца и строки посредством некоторой матрицы (линейного оператора).

6. Для заданной матрицы найти транспонированную и обратную матрицы.

7. Для заданной матрицы рассчитать определитель, перманент и след.

7. Для заданной матрицы найти собственные векторы и собственные значения.

8. Построить матричные представления для заданных операций симметрии, указать их инвариантные подпространства.

Список рекомендуемой литературы

Ван дер Варден Б.Л. Алгебра. М.: Наука, 1979, глава 1.

Дмитриев И.С. Симметрия в мире молекул. Л.: Химия, 1976.

Дмитриев И.С. Молекулы без химических связей. Л.: Химия, 1980.

Заградник Р., Полак Р. Основы квантовой химии. М.: Мир, 1979.

Ланкастер П. Теория матриц. М.: Наука. 1982.

Степанов Н.Ф., Ерлыкина М.Е., Филиппов Г.Г. Методы линейной алгебры в физической химии. М.: Изд-во МГУ, 1976.

Фларри Р. Группы симметрии. Теория и химические приложения. М.: Мир, 1983.

Фрид Э. Элементарное введение в абстрактную алгебру. М.: Мир, 1979, главы 3, 4.

Эллиот Дж., Добер П. Симметрия в физике. Т. 1 и 2. М.: Мир. 1983.

Источник

спектр матрицы

Смотреть что такое «спектр матрицы» в других словарях:

СПЕКТР МАТРИЦЫ — совокупность ее собственных значений. См. также Характеристический многочлен матрицы … Математическая энциклопедия

Спектр матрицы — … Википедия

Спектр (значения) — Спектр: Содержание 1 Математика и физика 2 Космические исследования 3 Товары и изделия … Википедия

Спектр — У этого термина существуют и другие значения, см. Спектр (значения). Спектр (лат. spectrum «видение») в физике распределение значений физической величины (обычно энергии, частоты или массы). Графическое представление такого… … Википедия

СПЕКТР ОПЕРАТОРА — обобщение на бесконечномерный случай понятиямножества собственных значений матрицы линейного преобразованияв конечномерном векторном пространстве. Если М такая n X n матрица, то её собств. значения это комплексные числа, для к рых ур пие имеет… … Физическая энциклопедия

Спектр оператора — У этого термина существуют и другие значения, см. Спектр (значения). Спектр оператора множество чисел, характеризующее линейный оператор. Применяется в линейной алгебре, функциональном анализе и квантовой механике. Содержание 1… … Википедия

Спектр оператора — (математический) совокупность чисел λ, для которых оператор Т λЕ (где Т данный линейный оператор, а Е единичный оператор) не имеет всюду определённого ограниченного обратного оператора. Понятие С. о. есть обобщение понятия совокупности… … Большая советская энциклопедия

Оптический спектр — Солнечный свет после прохождения через треугольную стеклянную призму Спектр (лат. spectrum от лат. spectare смотреть) в физике распределение значений физической величины (обычно энергии, частоты или массы), а также графическое представление… … Википедия

Световой спектр — Солнечный свет после прохождения через треугольную стеклянную призму Спектр (лат. spectrum от лат. spectare смотреть) в физике распределение значений физической величины (обычно энергии, частоты или массы), а также графическое представление… … Википедия

ШРЁДИНГЕРА ОПЕРАТОРА СПЕКТР — множество собств. значений оператора Шрёдингера (OШ): где гамильтониан оператор полной энергии системы (в том случае, когда потенциал не зависит от времени), и операторы кинет … Физическая энциклопедия

Ионизация лазерной десорбцией при содействии матрицы — Матрично активированная лазерная десорбция/ионизация, МАЛДИ (от англ. MALDI, Matrix Assisted Laser Desorption/Ionization десорбционный метод «мягкой» ионизации, обусловленной воздействием импульсами лазерного излучения на матрицу с анализируемым… … Википедия

Источник