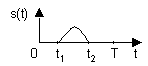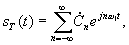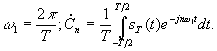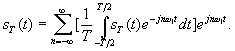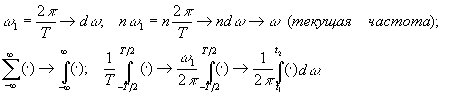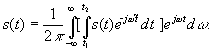Что такое спектральная плотность сигнала

Однако в этой статье основное внимание уделяется ситуациям, в которых временные ряды известны (по крайней мере, в статистическом смысле) или непосредственно измерены (например, с помощью микрофона, производимого компьютером). Спектр мощности важен в статистическая обработка сигналов и в статистическом исследовании случайные процессы, а также во многих других отраслях физика и инженерное дело. Обычно процесс является функцией времени, но можно аналогичным образом обсудить данные в пространственной области, разлагаемые с точки зрения пространственная частота. [3]

Содержание

Объяснение

Любой сигнал, который можно представить как переменную, изменяющуюся во времени, имеет соответствующий частотный спектр. Сюда входят знакомые объекты, такие как видимый свет (воспринимается как цвет), музыкальные ноты (воспринимаются как подача), радио / ТВ (определяется их частотой, а иногда длина волны) и даже регулярное вращение земли. Когда эти сигналы рассматриваются в форме частотного спектра, выявляются определенные аспекты принимаемых сигналов или лежащие в основе процессы, их производящие. В некоторых случаях частотный спектр может включать отчетливый пик, соответствующий синусоидальная волна составная часть. И дополнительно могут быть пики, соответствующие гармоники основного пика, указывающего на периодический сигнал, который нет просто синусоидальный. Или непрерывный спектр может показывать узкие частотные интервалы, которые сильно усиливаются в соответствии с резонансами, или частотные интервалы, содержащие почти нулевую мощность, как если бы режекторный фильтр.

В физика, сигнал может быть волной, например электромагнитная волна, акустическая волна, или вибрация механизма. В спектральная плотность мощности (PSD) сигнала описывает мощность присутствует в сигнале как функция частоты на единицу частоты. Спектральная плотность мощности обычно выражается в Вт на герц (Вт / Гц). [4]

Когда сигнал определяется только с точки зрения Напряжениенапример, не существует уникальной мощности, связанной с указанной амплитудой. В этом случае «мощность» просто рассчитывается в единицах квадрата сигнала, так как это всегда будет пропорциональный к фактической мощности, передаваемой этим сигналом в данный сопротивление. Таким образом, можно использовать единицы V 2 Гц −1 для PSD и V 2 с Гц −1 для ОУР (спектральная плотность энергии) [5] даже при том, что никакая фактическая «мощность» или «энергия» не указана.

В общем случае единицы PSD будут отношением единиц отклонения на единицу частоты; так, например, серия значений смещения (в метрах) с течением времени (в секундах) будет иметь PSD в единицах m 2 / Гц. Для анализа случайной вибрации, единицы измерения грамм 2 Гц −1 часто используются для PSD ускорение. Здесь грамм обозначает перегрузка. [7]

Математически нет необходимости назначать физические размеры сигналу или независимой переменной. В следующем обсуждении значение х (т) останется неопределенным, но предполагается, что это независимая переменная времени.

Определение

Спектральная плотность энергии

Спектральная плотность энергии наиболее подходит для переходных процессов, то есть импульсных сигналов, имеющих конечную общую энергию. Конечное или нет, Теорема Парсеваля [9] (или теорема Планшереля) дает нам альтернативное выражение для энергии сигнала:

Икс ^ ( ж ) = ∫ − ∞ ∞ е − я 2 π ж т Икс ( т ) d т < displaystyle < hat > (е) = int _ <- infty>^ < infty>e ^ <- i2 pi ft>x (t) dt>

Спектральная плотность мощности

Тогда спектральная плотность мощности просто определяется как подынтегральное выражение выше. [11] [12]

Источник

Спектральные плотности некоторых сигналов

DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов

Распространяется под лицензией LGPL v3

Спектральная плотность прямоугольного импульса равна:

Рассмотрим треугольный импульс длительности и амплитуды :

Для рассмотрения спектральной плотности треугольного импульса мы не будем вычислять интеграл Фурье непосредственно, потому что это потребует громоздких выкладок, а воспользуемся свойством преобразования Фурье свертки двух сигналов.

Можно заметить, что треугольный импульс длительности и амплитуды может быть представлен как результат свертки прямоугольного импульса длительности и амплитуды c самим собой, как это показано на рисунке 3.

Таким образом, мы можем применить свойство преобразования Фурье свертки сигналов и записать спектральную плотность треугольного импульса как квадрат спектральной плотности прямоугольного импульса длительности и амплитуды :

Гауссов импульс задается выражением:

График гауссова импульса при различном значении и показан на рисунке 4а.

Рассмотрим спектральную плотность гауссова импульса:

График спектральной плотности гауссова импульса для различного значения параметра показан на рисунке 4б. C увеличением увеличивается ширина гауссова импульса во временно́й области, и сужение спектральной плотности. При этом, убывание импульса во времени и по частоте носит экспоненциальный характер.

Как можно видеть из рисунка 5а, увеличение параметра приводит к сужению импульса во временно́й области.

Рассмотрим спектральную плотность двустороннего экспоненциального импульса:

Рассмотрим теперь односторонний экспоненциальный импульс, который получается из двустороннего при обнулении значения отрицательной полуоси времени:

Спектральная плотность одностороннего экспоненциального импульса равна:

Для получения спектральной плотности сигнала воспользуемся свойством двойственности преобразования Фурье, рассмотренным в в предыдущем параграфе. Тогда из выражения (2) можно записать:

В данном разделе мы рассмотрели спектральные плотности некоторых непериодических сигналов: прямоугольного, треугольного, гауссова импульса, а также одностороннего и двустороннего экспоненциальных импульсов.

Были приведены аналитические выражения для спектральных плотностей каждого из сигналов, а также их частотные свойства.

Источник

Спектральная плотность

В теории управления существуют и взаимно дополняют друг друга два подхода:

1) временнóй – исследование процессов во времени;

2) частотный – исследование частотных свойств сигналов и систем (с помощью передаточных функций и частотных характеристик).

Аналогичная ситуация наблюдается и при рассмотрении случайных процессов. Основная временная характеристика стационарного процесса – это корреляционная функция, а частотные свойства описываются спектральной плотностью.

Спектральная плотность – это функция, которая показывает распределение мощности сигнала по частотам. Такая информация о полезных сигналах, помехах и возмущениях очень важна для разработчика систем управления. Система должна быть спроектирована так, чтобы усиливать сигналы с «полезными» частотами и подавлять «вредные» частоты, характерные для помех и возмущений.

Для перехода от временнóго описания детерминированных (не случайных) процессов к частотному, используют преобразования Фурье и Лапласа. Аналогично спектральная плотность случайного процесса может быть найдена как преобразование Фурье от корреляционной функции[4]:

.

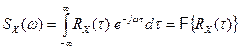
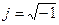
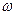
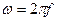
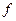
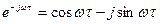
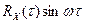
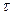
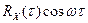
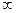
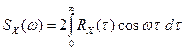
Здесь – мнимая единица, а – угловая частота в рад/с ( , где – «обычная» частота в герцах). Используя формулу Эйлера, можно представить экспоненту в виде сумму вещественной (косинусной) и мнимой (синусной) составляющих: . Функция – нечетная по , поэтому интеграл от нее в симметричных пределах равен нулю. Напротив, функция – четная, так что при интегрировании можно взять интервал от 0 до и удвоить результат:

.

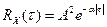
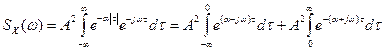
Спектральная плотность случайного процесса, имеющего корреляционную функцию , вычисляется как

.

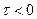
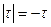
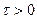
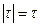
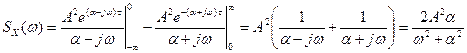
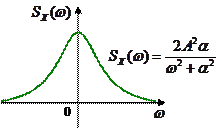
Интервал интегрирования разбит на две части. При имеем , а при – . Выполняя интегрирование, получаем

.

На рисунке слева показана корреляционная функция, а справа – соответствующая ей спектральная плотность мощности:

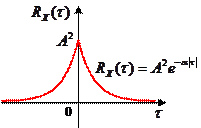Свойства спектральной плотности:

1) это неотрицательная, четная функция угловой частоты 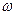(график расположен выше оси абсцисс и симметричен относительно вертикальной оси);

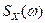
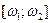
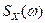
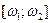
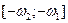
2) интеграл от на некотором интервале частот дает мощность, которая связана с этими частотами; поскольку функция – четная, результат интегрирования на нужно удвоить, чтобы учесть также и полосу ;

3) площадь под кривой определяет средний квадрат случайного процесса (для центрированного процесса он равен дисперсии):

.

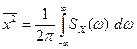
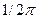
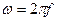
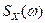
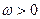
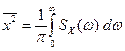
Множитель нужен для согласования единиц измерения, поскольку угловая частота измеряется не в герцах, а в рад/с. Учитывая, что функция четная, можно интегрировать ее только при , а результат удвоить:

.

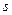
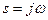
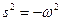
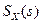
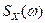
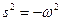
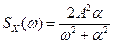
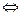
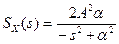
В теории управления нередко записывают спектральную плотность как функцию комплексной переменной , связанной с угловой частотой по формуле (отсюда следует ). Хотя это не совсем корректно с точки зрения математики, мы будем использовать запись для обозначения спектральной плотности , в которой выполнена замена :

.

Дата добавления: 2014-12-09 ; просмотров: 8298 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Пара преобразований Фурье. Спектральная плотность сигнала

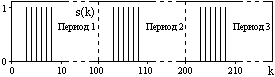
Обозначим периодический сигнал, полученный из s(t), в виде s_T(t). Тогда для него можно записать ряд Фурье

где

Подставим выражение для 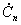в ряд:

Для того, чтобы перейти к функции s(t) следует в выражении s_T(t) устремить период к бесконечности. При этом число гармонических составляющих с частотами w =n2p /T будет бесконечно велико, расстояние между ними будет стремиться к нулю ( к бесконечно малой величине: 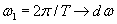, амплитуды составляющих также будут бесконечно малы. Поэтому говорить о спектре такого сигнала уже нельзя, т.к. спектр становится сплошным.

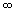
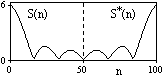
При предельном переходе в случае Т=> , имеем:

Таким образом, в пределе получаем

Внутренний интеграл является функцией частоты. Его называют спектральной плотностью сигнала, или частотной характеристикой сигнала и обозначают ,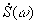

(*)

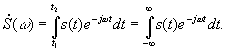Пределы интегрирования можно для общности поставить бесконечными, так как все равно там, где s(t) равна нулю, и интеграл равен нулю.

Выражение для спектральной плотности называют прямым преобразованием Фурье. Обратное преобразование Фурье определяет временную функцию сигнала по его спектральной плотности:

(**)

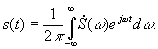9. Свойства преобразования Фурье. Свойства линейности, изменения масштаба времени, другие. Теореме о спектре производной. Теорема о спектре интеграла.

10. Дискретное преобразование Фурье. Помехи радиоприёму. Классификация помех.

Дискретное преобразование Фурьеможет быть получено непосредственно из интегрального преобразования дискретизаций аргументов (t_k = kDt, f_n = nDf):

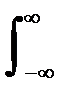
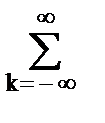
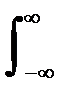
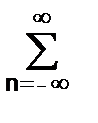
S(f) = s(t) exp(-j2pft) dt, S(f_n) = Dt s(t_k) exp(-j2pf_nkDt), (6.1.1)

s(t) = S(f) exp(j2pft) df, s(t_k) = Df S(f_n) exp(j2pnDft_k). (6.1.2)

Df = 1/T = 1/(NDt), Dt = 1/2f_N = 1/(NDf), DtDf = 1/N, N = 2Tf_N. (6.1.3)

При дискретном представлении сигналов аргумент t_k обычно проставляется номерами отсчетов k (по умолчанию Dt = 1, k = 0,1,…N-1), а преобразования Фурье выполняются по аргументу n (номер шага по частоте) на главных периодах. При значениях N, кратных 2:

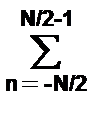
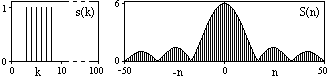
s(t_k) º s_k = (1/N) S_n exp(j2pkn/N), k = 0,1,…,N-1. (6.1.5)

В вычислительных операциях на ЭВМ для исключения отрицательных частотных аргументов (отрицательных значений номеров n) и использования идентичных алгоритмов прямого и обратного преобразования Фурье главный период спектра обычно принимается в интервале от 0 до 2f_N (0 £ n £ N), а суммирование в (6.1.5) производится соответственно от 0 до N-1. При этом следует учитывать, что комплексно сопряженным отсчетам S_n* интервала (-N,0) двустороннего спектра в интервале 0-2f_N соответствуют отсчеты S_N+1-n (т.е. сопряженными отсчетами в интервале 0-2f_N являются отсчеты S_n и S_N+1-n).

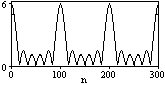
Рис. 6.1.1. Дискретный сигнал и модуль его спектра.

На рис. 6.1.2 приведена огибающая значений другой формы представления главного диапазона спектра. Независимо от формы представления спектр периодичен, в чем нетрудно убедиться, если вычислить значения спектра для большего интервала аргумента n с сохранением того же шага по частоте, как это показано на рис. 6.1.3 для огибающей значений спектра.

Рис. 6.1.2. Модуль спектра. Рис. 6.1.3. Модуль спектра.

На рис. 6.1.4. показано обратное преобразование Фурье для дискретного спектра, выполненное по формуле s'(k) =(1/100) 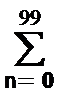S(n)×exp(j2pkn/100), которое показывает периодизацию исходной функции s(k), но главный период k= <0,99>этой функции полностью совпадает с исходным сигналом s(k).

Рис. 6.1.4. Обратное преобразование Фурье.

Преобразования (6.1.4-6.1.5) называют дискретными преобразованиями Фурье (ДПФ). Для ДПФ, в принципе, справедливы все свойства интегральных преобразований Фурье, однако при этом следует учитывать периодичность дискретных функций и спектров. Произведению спектров двух дискретных функций (при выполнении каких-либо операций при обработке сигналов в частотном представлении, как, например, фильтрации сигналов непосредственно в частотной форме) будет соответствовать свертка периодизированных функций во временном представлении (и наоборот). Такая свертка называется циклической (см. раздел 6.4) и ее результаты на концевых участках информационных интервалов могут существенно отличаться от свертки финитных дискретных функций (линейной свертки).

Из выражений ДПФ можно видеть, что для вычисления каждой гармоники нужно N операций комплексного умножения и сложения и соответственно N 2 операций на полное выполнение ДПФ. При больших объемах массивов данных это может приводить к существенным временным затратам. Ускорение вычислений достигается при использовании быстрого преобразования Фурье.

Помехи

Помехами обычно называют посторонние электрические возмущения, накладывающиеся на передаваемый сигнал и затрудняющие его прием. При большой интенсивности помех прием становится практически невозможным.

а) помехи от соседних радиопередатчиков (станций);

б) помехи от промышленных установок;

в) атмосферные помехи (грозы, осадки);

г) помехи, обусловленные прохождением электромагнитных волн через слои атмосферы: тропосферу, ионосферу;

д) тепловые и дробовые шумы в элементах радиоцепей, обусловленные тепловым движением электронов.

Математически сигнал на входе приемника можно представить либо в виде суммы передаваемого сигнала и помехи, и тогда помеху называют аддитивной, либо просто шумом, либо в виде произведения передаваемого сигнала и помехи, и тогда такую помеху называют мультипликативной. Эта помеха приводит к значительным изменениям интенсивности сигнала на входе приемника и объясняет такие явления как замирания.

Наличие помех затрудняет прием сигналов при большой интенсивности помех, распознавание сигнала может стать практически невозможным. Способность системы противостоять мешающему воздействию помехи носит название помехоустойчивости.

Внешние естественные активные помехи представляют собой шумы, возникающие в результате радиоизлучения земной поверхности и космических объектов, работы других радиоэлектронных средств. Комплекс мероприятий, направленных на уменьшение влияния взаимных помех РЭС, называется электомагнитной совместимостью. Этот комплекс включает в себя как технические меры совершенствования радиоаппаратуры, выбор формы сигнала и способа его обработки, так и организационные меры: регламентация частоты, разнесение РЭС в пространстве, нормирование уровня внеполосных и побочных излучений и др.

11. Дискретизация непрерывных сигналов. Теорема Котельникова (отсчётов). Понятие частоты Найквиста. Понятие интервала дискретизации.

Источник