Что такое спец математика
Разделы математики
Существует три официальных способа подразделения математики.
Содержание
Математика как специальность
Математика как специальность научных работников министерства науки и технологий Российской Федерации [1] подразделяется на научные специальности
Математика как учебная дисциплина
Математика как учебная дисциплина подразделяется в Российской Федерации на элементарную математику, изучаемую в средней школе, и образованную дисциплинами:
и высшую математику, изучаемую в ВУЗе. Дисциплины, входящие в состав высшей математики, варьируются в зависимости от специальности. Программа обучения по специальности математика [2] образована следующими учебными дисциплинами:
Знаком (ф) отмечены дисциплины, которые изучаются при обучении по специальности «физика».
Систематизация научных работ
Для систематизации научных работ используется Универсальная десятичная классификация 51.
Примечания
Полезное
Смотреть что такое «Разделы математики» в других словарях:
МАТЕМАТИКИ ИСТОРИЯ — Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом… … Энциклопедия Кольера
История математики — История науки … Википедия
История математики в России — Данная статья часть обзора История математики. Содержание 1 Древность и средневековье 2 XVII век 3 … Википедия
Философия математики — учение о сущности математического знания и о базовых принципах математических доказательств, раздел философии науки; её можно также назвать «метаматематикой». Содержание 1 Возможность оснований математики 2 Литература … Википедия
История математики в Индии — Данная статья часть обзора История математики. Научные достижения индийской математики широки и многообразны. Уже в древние времена учёные Индии на своём, во многом оригинальном пути развития достигли высокого уровня математических знаний.… … Википедия
Институт математики и механики (НИИММ СПбГУ) — Научно исследовательский институт математики и механики имени академика В. И. Смирнова (НИИММ СПбГУ) структурное подразделение Санкт Петербургского государственного университета. Выполняет организационную роль, является материальной базой для… … Википедия
Математика — Евклид. Деталь «Афинской школы» Рафаэля Математика (от др. греч … Википедия
Дискретная математика — Дискретная математика область математики, занимающаяся изучением дискретных структур, которые возникают как в пределах самой математики, так и в её приложениях. К числу таких структур могут быть отнесены конечные группы, конечные графы, а… … Википедия
Математический анализ — У этого термина существуют и другие значения, см. Анализ. Математический анализ совокупность разделов математики, посвящённых исследованию функций и их обобщений методами дифференциального и интегрального исчислений. При столь общей… … Википедия
МЕТОД АКСИОМАТИЧЕСКИЙ — способ построения теории, при к ром в ее основу кладутся нек рые ее положения – аксиомы или постулаты, – из к рых все остальные положения теории (теоремы) выводятся путем рассуждений, называемых д о к а з а т е л ь с т в а м и. Правила, по к рым… … Философская энциклопедия
Специальная математика
Пермский Государственный Технический Университет
для студентов специальности АСУ
1. Теория множеств 6
1.1 Понятие множества 6
1.2. Операции над множествами 7
1.4. Алгебра множеств 9
1.5. Кортеж. График 10
1.6. Соответствия 12
1.7.1 Отношение эквивалентности 13
1.7.2. Отношения порядка 14
1.8.1. Диаграммы Хассе 15
1.8.2. Понятие решетки 16
1.8.3. Алгебраическое представление решеток. 17
1.8.5. Морфизмы решеток 18
1.9. Мощность множества 18
1.9.1. Понятие мощности 19
1.9.2. Аксиоматика Пеано 19
1.9.3. Сравнение мощностей 19
1.9.4. Мощность множества R. 20
Теорема Кантора 20
1.9.5. Арифметика бесконечного 21
1.9.6. Противопоставление системного и 21
теоретико-множественного подходов 21
2. Математическая логика 21
2.1. Логика высказываний 21
2.1.1. Операции над высказываниями 22
2.1.2. Построение и анализ сложных высказываний 22
2.1.3. Алгебра высказываний 24
2.1.4. Формы представления высказываний 24
2.1.5. Преобразование высказываний 25
2.1.6. Минимизация высказываний методом Квайна 26
2.1.7. Минимизация с помощью карт Вейча 28
2.1.8. Функциональная полнота 29
2.2. Логика предикатов 30
2.2.1. Основные равносильности для предикатов 30
2.2.2. Получение дизъюнктов 31
2.3. Аксиоматические теории 32
2.3.1. Аксиоматическая теория исчисления высказываний 32
2.3.2. Непротиворечивость и полнота аксиоматической теории исчисления высказываний 33
2.4. Аксиоматические теории первого порядка 34
2.5. Метод резолюций 35
2.6. Система Генцена 37
2.7. Система Аристотеля 39
2.8. Примеры неклассических логик 41
3. Теория Автоматов 43
3.1. Понятие автомата 43
3.2. Примеры автоматов 43
3.3. Минимизация автоматов 45
3.4. Особенности минимизации автомата Мура 46
3.5. Переход от автомата Мура к автомату Мили и наоборот 47
4.1. Понятие графа 48
4.2. Теорема Эйлера 51
4.3. Полные графы и деревья 53
4.5. Алгоритм Краскала 55
4.6. Планарные графы 56
4.7. Задача о 4 красках 57
4.8. Определение путей в графе 58
4.9. Приведение графа к ярусно-параллельной форме 59
4.10. Внутренняя устойчивость графа 60
4.11. Множество внешней устойчивости. 61
5.1. Понятие группы 63
5.2. Морфизмы групп 63
5.3. Инвариантные (нормальные) подгруппы 65
5.4. Группа Диэдра (D3) 66
5.5. Смежные классы 67
5.6. Фактор-группы 67
5.7. Группа Клейна четвертой степени 68
6. Теория алгоритмов 68
6.1. Понятие алгоритма 68
6.2. Конкретизация понятия алгоритма 69
6.3. Сложность вычислений 69
6.4. Машины Тьюринга 70
6.5. Нормальные алгорифмы Маркова 71
6.6. Рекурсивные функции 72
7. Формальные грамматики 76
7.1. Понятие формальной грамматики 76
7.2. Деревья вывода 77
7.3. Классификация языков по Хомскому 78
7.4. Распознающие автоматы 79
7.5. Понятие транслятора 80
7.6. Основные функции компилятора. 81
Лексический анализ 81
7.7. Переход от недетерминированного распознающего автомата к 81
7.8. Переход от праволинейной грамматики к автоматной 82
7.10. Детерминированные автоматы с магазинной памятью 85
7.11. Транслирующие грамматики 86
7.14. Метод рекурсивного спуска 89
7.16. Функции предшествования 93
7.17. Атрибутные грамматики 94
7.19. Область действия и передача параметров 96
7.20. Генерация выходного текста. 97
Польская инверсная запись 97
7.21. Оптимизация программ 100
8. Функциональное программирование 101
9. Логическое программирование. 104
10. Объектно-ориентированное программирование 105
Введение
Специальная математика – это некоторые разделы современной математики. Речь идет о математическом аппарате, который помогает расширить возможности математического описания или, выражаясь изящнее – математического моделирования, сложных систем. Далеко не все задачи, которые возникают в сложных системах, включающих человека, можно свести к задачам механики или математического анализа, традиционно называемого в технических вузах «высшей математикой».
Самостоятельное значение имеют математические проблемы теоретического и практического программирования.
А что касается классификации, то относить ли, например, теорию графов к дискретной математике или к топологии – тоже вопрос. Отнесение к дискретной математике теории групп еще более условно.
Задача данного курса состоит в выработке навыков формализации физических сущностей с помощью различных «диалектов» современного математического языка. И наоборот, интерпретации полученных математических результатов.
Содержательный аспект обычно предшествует формализации и имеет для нас значение при осмыслении результатов математических манипуляций.
Так что акцент в большей степени сделан на понятийной, а не вычислительной стороне ряда разделов математики.
1. Теория множеств
1.1 Понятие множества
Теорию множеств можно подразделить на аксиоматическую и интуитивную (наивную).
Для интуитивного понятия множества существенны два момента, следующие из «определения»:
1. Различимость элементов.
Студенты образуют группу. Деревья составляют лес.
Целые числа составляют множество целых чисел.
Множество, не содержащее элементов, называется пустым множеством и обозначается или . Обычно именно фигурные скобки используются для выделения множества (отсутствие элементов в скобках и говорит о том, что это пустое множество).
Включать ли самого себя в множество тех, кого он обязан брить?!
Способы задания множеств:
A =
B =
Например, студенческая группа студенты данной специальности
Например: множество отличников
Кстати, на что намекает это отношение?
Свойства отношения включения:
1. Рефлексивность : A A
2. Принцип объемности : A B и B A следует B = A (на основе этого принципа и доказывается равенство двух множеств).
3. Транзитивность : A B и B C следует A C
1.2. Операции над множествами
1. Объединение множеств A и B
2. Пересечение множеств A и B
3. Разность множеств A и B
4. Симметрическая разность множеств A и B
5
A 
Пусть А = <1, 2, 3>и B = <3,4>, тогда
А 
Диаграммы Эйлера-Венна позволяют представить множества, как множества точек на плоскости, оганиченные замкнутыми кривыми круглой или овальной формы. Прямоугольная рамка ограничивает универсум. Обычно, если не требуется иное, рисуют так называемый общий случай: когда каждое из множеств имеет свои собственные точки и точки, общие с другими множествами.
Диаграмма для общего случая c тремя множествами будет иметь вид:
Построение диаграммы Эйлера-Венна для общего случая с четырьмя и более множествами можно предложить для самостоятельных развлечений.
1.4. Алгебра множеств
Операции над множествами дают в результате новые множества.
Для операций справедлив ряд законов. Приведем наиболее часто используемые.
Для упрощения записи, уменьшения числа скобок, определяющих последовательность операций, можно использовать соглашение о «силе» операций (в порядке убывания): дополнение, пересечение, объединение.
Остальные операции можно выразить через эти три.



A (B C) = (A B) C = A B C A (B C) = (A B) C = A B С
A (B С)= (A B) (A C) A (B С) = (A B) (A C)
A (A B) = A A (A B) = A
6. Исключенного третьего: Противоречия:








Пример доказательства варианта дистрибутивного закона :
A (B С) = (A B) (A C)
I. Докажем, что левая часть включена в правую:
A (B C) (A B) (A C)
Пусть х А (В С), тогда у х есть две возможности
2. х B C. Тогда х B и х C х A B и х A C,
то есть х (A B) (A C).
II. Докажем, что правая часть включена в левую:
(A B) (A C) A B C.
Пусть х A B и х A C. Тогда возможны два варианта:
1. х A х A B C
2. х B и х C х B C х A B C.
То есть левое и правое множества равны.
1.5. Кортеж. График
В кортеже существенны не только элементы, но и порядок, в котором они располагаются. Следовательно, кортеж может содержать одинаковые элементы.
Примерами кортежей могут служить очередь, свадебный кортеж. Кортежем является вектор, заданный проекциями на оси.
Кортеж заключается в угловые скобки.
— упорядоченная тройка – единичный вектор.
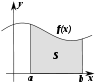
Несколько эпатирующе звучит слово график применительно к аналитической записи. Но это лишь подчеркивает его универсальность. Для множеств действительных чисел Х и У приведем графический пример графика.
Декартово (прямое) произведение множеств A и B:
Пример : Для A = < 1, 2>и B= < 1, 2, 3>декартово произведение
Q. Очевидно, что это некоммутативная операция.
4. График называется диагональю множества М, если он состоит из пар вида

Проекция некоторого множества М на множество осей дает множество проекций кортежей, составляющих множество. Исходное множество должно состоять из кортежей одинаковой длины.
1.6. Соответствия
5. Соответствие называется биективным (взаимно-однозначным), если оно функционально, инъективно, всюдуопределено и сюръективно.
Пример : Соответствие «студенты сдавали экзамен». (Трифонов не пришел).
X
Y
Y = <2, 3, 4, 5>– множество возможных оценок.
Соответствие функционально, неинъективно, невсюдуопределено, несюръективно, небиективно.
Пример : Соответствие «покупателей и купленных товаров».
X
Типовая ситуация для такого соответствия: нефункционально, инъективно, невсюду определено, несюръективно, небиективно.
Математика
Содержание
Основные сведения
Идеализированные свойства исследуемых объектов либо формулируются в виде аксиом, либо перечисляются в определении соответствующих математических объектов. Затем по строгим правилам логического вывода из этих свойств выводятся другие истинные свойства (теоремы). Эта теория в совокупности образует математическую модель исследуемого объекта. Таким образом первоначально, исходя из пространственных и количественных соотношений, математика получает более абстрактные соотношения, изучение которых также является предметом современной математики.
Традиционно математика делится на теоретическую, выполняющую углублённый анализ внутриматематических структур, и прикладную, предоставляющую свои модели другим наукам и инженерным дисциплинам, причём некоторые из них занимают пограничное с математикой положение. В частности, формальная логика может рассматриваться и как часть философских наук, и как часть математических наук; механика — и физика, и математика; информатика, компьютерные технологии и алгоритмика относятся как к инженерии, так и к математическим наукам и т. д. В литературе было предложено много различных определений математики (см. ниже).
Этимология
В текстах на русском языке слово «математика» или «мафематика» встречается по крайней мере с XVII века, например, у Николая Спафария в «Книге избранной вкратце о девяти мусах и о седмих свободных художествах» (1672 год) [5]
Определения
Одно из первых определений предмета математики дал Декарт [6] :
К области математики относятся только те науки, в которых рассматривается либо порядок, либо мера и совершенно не существенно, будут ли это числа, фигуры, звёзды, звуки или что-нибудь другое, в чём отыскивается эта мера. Таким образом, должна существовать некая общая наука, объясняющая всё относящееся к порядку и мере, не входя в исследование никаких частных предметов, и эта наука должна называться не иностранным, но старым, уже вошедшим в употребление именем Всеобщей математики.
Математика… наука о количественных отношениях и пространственных формах действительного мира.
Это определение Энгельса [8] ; правда, далее Колмогоров поясняет, что все использованные термины надо понимать в самом расширенном и абстрактном смысле.
Сущность математики… представляется теперь как учение об отношениях между объектами, о которых ничего не известно, кроме описывающих их некоторых свойств,— именно тех, которые в качестве аксиом положены в основание теории… Математика есть набор абстрактных форм — математических структур.
Приведём ещё несколько современных определений.
Герман Вейль пессимистически оценил возможность дать общепринятое определение предмета математики:
Вопрос об основаниях математики и о том, что представляет собой в конечном счёте математика, остаётся открытым. Мы не знаем какого-то направления, которое позволит в конце концов найти окончательный ответ на этот вопрос, и можно ли вообще ожидать, что подобный «окончательный» ответ будет когда-нибудь получен и признан всеми математиками.
Разделы математики
1. Математика как учебная дисциплина подразделяется в Российской Федерации на элементарную математику, изучаемую в средней школе и образованную дисциплинами:
и высшую математику, изучаемую на нематематических специальностях вузов. Дисциплины, входящие в состав высшей математики, варьируются в зависимости от специальности.
Программа обучения по специальности математика [13] образована следующими учебными дисциплинами:
2. Математика как специальность научных работников Министерством образования и науки Российской Федерации [14] подразделяется на специальности:
3. Для систематизации научных работ используется раздел «Математика» [15] универсальной десятичной классификации (УДК).
4. Американское математическое общество (AMS) выработало свой стандарт для классификации разделов математики. Он называется Mathematics Subject Classification. Этот стандарт периодически обновляется. Текущая версия — это MSC 2010. Предыдущая версия — MSC 2000.
Обозначения
Вследствие того, что математика работает с чрезвычайно разнообразными и довольно сложными структурами, система обозначений также очень сложна. Современная система записи формул сформировалась на основе европейской алгебраической традиции, а также математического анализа (понятия функции, производной и т. д.). Геометрия испокон века пользовалась наглядным (геометрическим же) представлением. В современной математике распространены также сложные графические системы записи (например, коммутативные диаграммы), нередко также применяются обозначения на основе графов.
Краткая история
Академиком А. Н. Колмогоровым предложена такая структура истории математики:
Развитие математики началось вместе с тем, как человек стал использовать абстракции сколько-нибудь высокого уровня. Простая абстракция — числа; осмысление того, что два яблока и два апельсина, несмотря на все их различия, имеют что-то общее, а именно занимают обе руки одного человека, — качественное достижение мышления человека. Кроме того, что древние люди узнали, как считать конкретные объекты, они также поняли, как вычислять и абстрактные количества, такие, как время: дни, сезоны, года. Из элементарного счёта естественным образом начала развиваться арифметика: сложение, вычитание, умножение и деление чисел.
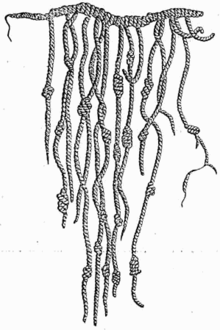
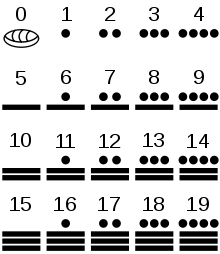
Развитие математики опирается на письменность и умение записывать числа. Наверно, древние люди сначала выражали количество путём рисования чёрточек на земле или выцарапывали их на древесине. Древние инки, не имея иной системы письменности, представляли и сохраняли числовые данные, используя сложную систему верёвочных узлов, так называемые кипу. Существовало множество различных систем счисления. Первые известные записи чисел были найдены в папирусе Ахмеса, созданном египтянами Среднего царства. Индская цивилизация разработала современную десятичную систему счисления, включающую концепцию нуля.
Исторически основные математические дисциплины появились под воздействием необходимости вести расчёты в коммерческой сфере, при измерении земель и для предсказания астрономических явлений и, позже, для решения новых физических задач. Каждая из этих сфер играет большую роль в широком развитии математики, заключающемся в изучении структур, пространств и изменений.
Философия математики
Цели и методы
Математика изучает воображаемые, идеальные объекты и соотношения между ними, используя формальный язык. В общем случае математические понятия и теоремы не обязательно имеют соответствие чему-либо в физическом мире. Главная задача прикладного раздела математики — создать математическую модель, достаточно адекватную исследуемому реальному объекту. Задача математика-теоретика — обеспечить достаточный набор удобных средств для достижения этой цели.
Содержание математики можно определить как систему математических моделей и инструментов для их создания. Модель объекта учитывает не все его черты, а только самые необходимые для целей изучения (идеализированные). Например, изучая физические свойства апельсина, мы можем абстрагироваться от его цвета и вкуса и представить его (пусть не идеально точно) шаром. Если же нам надо понять, сколько апельсинов получится, если мы сложим вместе два и три, — то можно абстрагироваться и от формы, оставив у модели только одну характеристику — количество. Абстракция и установление связей между объектами в самом общем виде — одно из главных направлений математического творчества.
Другое направление, наряду с абстрагированием — обобщение. Например, обобщая понятие «пространство» до пространства n-измерений. «Пространство 

Изучение внутриматематических объектов, как правило, происходит при помощи аксиоматического метода: сначала для исследуемых объектов формулируются список основных понятий и аксиом, а затем из аксиом с помощью правил вывода получают содержательные теоремы, в совокупности образующие математическую модель.
Основания
Вопрос сущности и оснований математики обсуждался со времён Платона. Начиная с XX века наблюдается сравнительное согласие в вопросе, что надлежит считать строгим математическим доказательством, однако отсутствует согласие в понимании того, что в математике считать изначально истинным. Отсюда вытекают разногласия как в вопросах аксиоматики и взаимосвязи отраслей математики, так и в выборе логических систем, которыми следует при доказательствах пользоваться.
Помимо скептического, известны нижеперечисленные подходы к данному вопросу.
Теоретико-множественный подход
Предлагается рассматривать все математические объекты в рамках теории множеств, чаще всего с аксиоматикой Цермело — Френкеля (хотя существует множество других, равносильных ей). Данный подход считается с середины XX века преобладающим, однако в действительности большинство математических работ не ставят задач перевести свои утверждения строго на язык теории множеств, а оперируют понятиями и фактами, установленными в некоторых областях математики. Таким образом, если в теории множеств будет обнаружено противоречие, это не повлечёт за собой обесценивание большинства результатов.
Логицизм
Данный подход предполагает строгую типизацию математических объектов. Многие парадоксы, избегаемые в теории множеств лишь путём специальных уловок, оказываются невозможными в принципе.
Формализм
Данный подход предполагает изучение формальных систем на основе классической логики.
Интуиционизм
Интуиционизм предполагает в основании математики интуиционистскую логику, более ограниченную в средствах доказательства (но, как считается, и более надёжную). Интуиционизм отвергает доказательство от противного, многие неконструктивные доказательства становятся невозможными, а многие проблемы теории множеств — бессмысленными (неформализуемыми).
Конструктивная математика
Основные темы
Числа
Понятие «число» первоначально относилось к натуральным числам. В дальнейшем оно было постепенно распространено на целые, рациональные, действительные, комплексные и другие числа.
| |||||||||||||||
 |  | ||||||||||||||
| Комплексные числа | Кватернионы | ||||||||||||||
 Числовые системы Числовые системы | |
|---|---|
| Счётные множества | Натуральные числа ( ) • Целые ( ) • Целые ( ) • Рациональные ( ) • Рациональные ( ) • Алгебраические ( ) • Алгебраические ( ) • Периоды • Вычислимые • Арифметические ) • Периоды • Вычислимые • Арифметические |
| Вещественные числа и их расширения | Вещественные ( ) • Комплексные ( ) • Комплексные ( ) • Кватернионы ( ) • Кватернионы ( ) • Числа Кэли (октавы, октонионы) ( ) • Числа Кэли (октавы, октонионы) ( ) • Седенионы ( ) • Седенионы ( ) • Альтернионы • Процедура Кэли — Диксона • Дуальные • Гиперкомплексные • Суперреальные • Гиперреальные • Surreal number (англ.) ) • Альтернионы • Процедура Кэли — Диксона • Дуальные • Гиперкомплексные • Суперреальные • Гиперреальные • Surreal number (англ.) |
| Другие числовые системы | Кардинальные числа • Порядковые числа (трансфинитные, ординал) • p-адические • Супернатуральные числа |
| См. также | Двойные числа • Иррациональные числа • Трансцендентные • Числовой луч • Бикватернион |
Преобразования
 |  |  |  |
| Арифметика | Дифференциальное и интегральное исчисление | Векторный анализ | Анализ |
 |  |  | |
| Дифференциальные уравнения | Динамические системы | Теория хаоса |
Структуры
Пространственные отношения
Более наглядные подходы в математике.
Дискретная математика
Дискретная математика включает средства, которые применяются над объектами, способными принимать только отдельные, не непрерывные значения.
 | 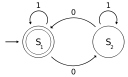 |  |  |
| Математическая логика | Теория вычислимости | Криптография | Теория графов |
Коды в системах классификации знаний
Онлайновые сервисы
Существует большое число сайтов, предоставляющих сервис для математических расчётов. Большинство из них англоязычные. [20] Из русскоязычных можно отметить сервис математических запросов поисковой системы Nigma.