Что такое спецификация атд
Абстрактные типы данных (АТД)
Полная спецификация
Спецификация стеков как АТД
Для всех x: G, s: STACK [G]
Ничего кроме правды
Сила спецификаций АТД проистекает из их способности отражать только существенные свойства структур данных без лишних деталей. Приведенная выше спецификация стеков выражает все, что нужно по существу знать о понятии стека, и не включает ничего, что относилось бы к каким-либо конкретным реализациям стеков. Это вся правда о стеках, и ничего кроме правды.
Такие спецификации задают общую модель вычислений на соответствующих структурах данных. Определенные в спецификации абстрактного типа данных функции позволяют строить сложные выражения, а аксиомы АТД позволяют упрощать такие выражения и получать более простые результаты. Сложное стековое выражение является математическим эквивалентом программы, а процесс упрощения является математическим эквивалентом вычисления или выполнения этой программы.
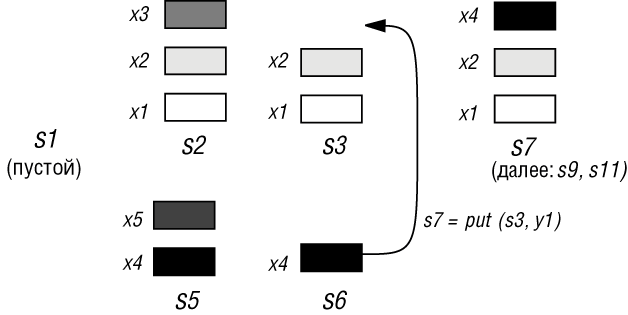
Вот пример. Рассмотрим для приведенной выше спецификации АТД STACK следующее выражение stackexp :
По-видимому, выражение stackexp будет проще понять, если мы представим его как последовательность вспомогательных выражений:
Можно легко найти значение такого АТД выражения, нарисовав последовательно несколько таких рисунков. (Здесь найдено x4 ). Но теория позволяет нам получить этот результат формально, не обращаясь к рисункам, а только последовательно применяя аксиомы для упрощения выражения, до тех пор, пока дальнейшее упрощение станет невозможным. Например:
Этот пример позволяет отметить одну из важнейших теоретических ролей абстрактных типов данных: они предоставляют формальную модель для понятий программы и выполнения программы. Эта модель чисто математическая: в ней нет императивных понятий состояния программы, переменных с изменяемыми во времени значениями, последовательности выполняемых действий. Она основана на обычных математических методах преобразования выражений.
Концепция Абстрактного Типа Данных
Доброго времени суток, хабравчане!
Следующий пост является изложением моих размышлений на тему природы классов и АТД. Эти размышления дополнены интересными цитатами из книг гуру разработки программного обеспечения
Введение
Начнем с того, что плавно подойдем к определению АТД. АТД, в первую очередь, представляет собой тип данных, что означет следущее:
наличие определенных доступных операций над элементами этого типа;
а также данные, относительно которых эти операции выполняются (диапазон значений).
Что же означает слово “абстрактный”? В первую очередь понятие “абстрактность” означет сосредоточение внимания на чем-то важном и, при этом, нам нужно отвлечься от неважных, на данный момент, деталей. Определение абстрактности хорошо раскрыто в книге Гради Буча (“Grady Booch”). Звучит определение так:
Абстракция – это выделение и придание совокупности объектов общих свойств, которые определяют их концепутальные границы и отличают от всех других видов объектов.
Иными словами, абстракция позволяет “пролить свет” на нужные нам данные объектов и, при этом, “затенить” те данные, которые нам не важны.
Итак, что же будет, если слить понятия “тип данных” и “абстракция” воедино? Мы получим тип данных, который предоставляет нам некий набор операций, обеспечивающих поведение объектов этого типа данных, а также этот тип данных будет скрывать те данные, с помощью которых реализовано данное поведение. Отсюда, приходим к понятию АТД:
АТД – это такой тип данных, который скрывает свою внутреннюю реализацию от клиентов.
Удивительно то, что путем применения абстракции АТД позволяет нам не задумываться над низкоуровневыми деталями реализации, а работать с высокоуровневой сущностью реального мира (Стив Макконнелл).
Я считаю, что при разработке АТД сначала нужно определить интерфейс, так как интерфейс не должен зависеть от внутреннего представления данных в АТД. После определения операций, сотставляющих интерфейс, нужно сосредоточиться на данных, которые и будут реализовать заданное поведение АТД. В итоге мы получим некую структуру данных – механизм позволяющий хранить и обрабатывать данные. При этом, прелесть АТД в том, что если нам захочется изменить внутренне представление данных, то нам не придется блуждать по всей программе и менять каждую строку кода, которая зависит от данных, которые мы хотим поменять. АТД инкапсулирует эти данные, что позволяет менять работу объектов этого типа, а не всей программы.
Преимущества АТД
Использование АТД имеет массу преимуществ (все описанные преимущества можно найти в книге Стива Макконнелла «Совершенный код”):
Стив Макконнелл рекомендует представлять в виде АТД низкоуровнеые типы данных, такие как стек или список. Спросите себя, что представляет собой этот список. Если он представляет список сотрудников банка, то и рассматривайте АТД как список сотрудников банка.
Итак, мы разобрались, что такое АТД и назвали преимущества его применения. Теперь стоит отметить, что при разработке классов в ООП следует думать, в первую очередь, об АТД. При этом, как сказал Стив МакКоннелл, Вы программируете не на языке, а с помощью языка. Т.е Вы будете программировать выходя за рамки языка, не ограничиваясь мыслями в терминах массивов или простых типов данных. Вместо этого Вы будете думать на высоком уровне абстракции (например, в терминах электронных таблицах или списков сотрудников). Класс – это не что иное как дополнение и способ реализации концепции АТД. Мы можем даже представить класс в виде формулы:
Класс = АТД + Наследование + Полиморфизм.
Так почему же следут думать об АТД, при разработке классов. Потому что, сперва мы должны решить какие операции будут составлять интерфейс будущего класса, какие данные скрыть, а к каким предоставить открытый доступ. Мы должны подумать об обеспечении высокой информативности интерфейса, легкости оптимизации и проверки кода, а также о том, как бы нам предоставить правильную абстракцию, чтобы можно было думать о сущностях реального мира, а не о низкоуровнеых деталях реализации. Я считаю, что именно после определения АТД мы должны думать о вопросах наследования и полиморфизма.
Стоит отметить, что концепция АТД нашла гирокое применение в ООП, т.к именно эта концепция дополняет ООП и позволяет уменшить сложность программ в быстроменяющемся мире требований к ПО.
Данную статью я писал для того, что бы обратить внимание разработчиков на АТД с целью повышения качества работы и разработки программного обеспечения.
Стив Макконнелл – “Совершенный код”;
Роберт Седжвик – «Алгоритмы на Java».
Абстрактные типы данных в программировании
Автор: Лапшин Владимир Анатольевич
Введение
Отличительной особенностью абстрактных типов данных как механизма абстракции является тот факт, что функциональность компонента программы, описываемая кластером операций, может быть реализована различными способами. Различные реализации абстрактных типов данных взаимозаменяемы благодаря механизму абстракции АТД, позволяющему скрыть детали реализации с помощью набора предопределенных операций.
Кроме собственно описания самой структуры данных, Кнут описывает «алгоритмы обработки» этой структуры с помощью словаря специальных терминов [3, стр. 281]. Для стека этот словарь содержит термины: push (втолкнуть), pop (вытолкнуть) и top (верхний элемент стека). Таким образом, типы данных описываются Кнутом с помощью специального языка, задающего определенную терминологию и толкование этой терминологии. Эта особенность описания была замечена Стивеном Жиллем в работе [4] и, таким образом, явилась одним из побудительных мотивов для осознания важности концепции АТД.
Парнас представлял модули как абстрактные машины, хранящие внутри себя состояния и позволяющие изменять это состояние посредством определенного набора операций. Эта концепция является базовой, как для концепции абстрактных типов данных, так и для объектно-ориентированного программирования.
Функциональная абстракция подразумевает выделение набора операций (функций) для работы с элементами программной модели. Таким образом, сущности программной модели представляются с помощью набора операций. Так осуществляется поведенческая абстракция сущности в программном коде. Сами авторы использовали термин «operational cluster», т.е. набор операций, и назвали такой набор операций абстрактным типом данных (АТД).
Рассмотрим определение абстрактного типа данных на языке, синтаксис которого унаследован преимущественно от языка PASCAL (детали можно найти в оригинальной работе). Этот язык поддерживает абстракцию модулей, доступ к которым задается посредством набора операций. Итак, определение типа «стек».
Здесь задается модуль с именем «stack» и для него определяется набор (cluster) операций: push, pop, top, erasetop, empty. От привычного всем программистам нашего времени набора операций со стеком этот кластер отличается только наличием операции erasetop, которая аналогична операции pop, но не возвращает значения. В библиотеке STL языка C++ операция pop шаблонного класса stack определена как erasetop, т.е. не возвращает удаляемого значения. Таким образом, это определение, сделанное в 1974 году, практически аналогично используемым сейчас определениям типа стек.
Для представления типа содержимого стека используется параметрический тип rep. Название унаследовано от термина «object representation» (представление объекта). По идее авторов, пользователи не имеют доступа к внутренним «объектам» модуля, но работают только с его «представлением», т.е. с типом rep. В данном случае rep является представлением внутренней реализации объектов «стека». Для каждого объекта стека фиксируется тип его элементов (e_type), поддерживается счетчик числа элементов в стеке (tp) и хранилище элементов в виде массива (stk).
Таким образом, согласно классическому определению, абстрактный тип данных представляется как кластер операций. Операции получают и возвращают аргументы определенных типов, поэтому для полноценного описания АТД необходимо еще эти типы определить. В большинстве случаев этого вполне достаточно, но можно было бы описать еще условия, которым должны удовлетворять все правильные реализации данного абстрактного типа данных. Эти условия легко можно сформировать в виде композиции операций, применяемых к объектам стека. Например, совершенно ясно, что вставив элемент в стек с помощью операции push, а затем, взяв элемент с вершины стека с помощью операции top, мы должны получить тот же элемент. Это утверждение можно сформулировать следующим образом:
Аналогичным образом можно сформулировать другие условия:
Все эти утверждения сформулированы в виде аксиом специального вида, т.н. аксиом в виде равенств. Кроме аксиом-равенств для абстрактных типов данных можно вводить еще т.н. предусловия, которые должны выполняться при применении операций к АТД. Для стека можно было бы ввести два таких предусловия, которые можно увидеть выше:
Подобное условие можно было бы ввести и для операции erasetop, но мы здесь этого делать не будем, чтобы не отступать от используемых в наше время определений.
Таким образом, абстрактный тип данных можно определить как четверку (типы, операции, аксиомы-равенства, предусловия). Подобные определения используются в языках алгебраических спецификаций, о которых будет рассказано чуть подробнее в одном из разделов ниже.
В следующем разделе на некоторых примерах будет показано, как концепция АТД используется в современных языках программирования.
Использование АТД в языках программирования
В большинстве современных императивных языков основной концепцией, используемой для описания абстракций в программном коде, является объектно-ориентированный подход. Объектно-ориентированное программирование (ООП) также, как и подход к программированию на основе АТД, является, в некоторой степени, развитием тех идей о модульном программировании, которые были заложены в упоминавшейся выше работе Дэвида Парнаса [4].
Одно из наиболее значимых отличий АТД от ООП заключается в том, что абстрактный тип не содержит данных и, тем более, каких либо состояний этих данных. Свойство абстракции АТД как раз и заключается в том, что абстрактный тип представляет собой поведенческую абстракцию, т.е. кластер операций, посредством которых производится взаимодействие с данными. Поведенческая абстракция целиком и полностью описывается спецификацией абстрактного типа данных. Реализация АТД должна соответствовать спецификации данного абстрактного типа, в этом и заключается абстракция на основе АТД. Подробнее о различиях концепций АТД и ООП можно прочитать в работе [6].
На практике, в языках программирования, которые поддерживают концепцию ООП, часто также реализуется и концепция АТД. Чтобы, согласно «бритве Оккама», не «множить сущее без необходимости», для реализации АТД используются средства ООП. Для этого абстрактный тип определяют как класс с определенным интерфейсом. После чего в качестве реализаций данного абстрактного типа выступают его объекты-наследники (в смысле наследования ООП). Работа с реализациями АТД ведется через интерфейс базового объекта, т.е. через операции данного АТД. Для этого обычно используется принцип подстановки Лисков [7], согласно которому объекты-наследники можно подставлять в аргументы, имеющие базовый тип.
Рассмотрим в качестве примера, как АТД реализуются в языке программирования C++. C++ является языком, поддерживающим ООП на основе т.н. механизма классов. Абстрактный тип данных определяется как класс, предоставляющий т.н. «чисто виртуальные методы». Для иллюстрации рассмотрим пример реализации АТД стека целочисленных значений на C++:
Здесь, ввиду особенностей реализации объектов на C++, объекты АТД Stack передаются в операции и возвращаются из них неявно, в виде скрытых параметров. Поэтому аргументы операций почти ничем не отличаются от тех, что описаны в спецификации АТД «стек» выше.
В языке C++ любой класс, объявляющий чисто виртуальный метод (т.е. приравненный нулю при объявлении), называется «абстрактным типом». Это, конечно, еще не абстрактный тип данных, но уже нечто методологически на него похожее. Экземпляры абстрактных типов создавать нельзя. Таким образом, абстрактные типы используются в C++ для определения интерфейсов (кластеров операций), т.е. реализуют в несколько усеченном виде концепцию АТД.
Для задания реализации абстрактных типов в языке C++ используется механизм наследования и переопределения, объявленных в базовом классе методов-операций. Вот, например, как будет выглядеть реализация стека на основе массива:
В реализации используется тип std::vector стандартной библиотеки языка C++. Это параметризованный тип, реализующий концепцию «динамического массива значений». Тип предоставляет методы для вставки/удаления значений в конец массива. Также имеются методы для доступа к последнему элементу массива и проверки массива на непустоту. При невыполнении предусловий на операции pop и top генерируется исключение.
В языке C++ принцип подстановки Лисков реализуется на типах «указателей на объекты классов» и на ссылках. Указатель представляет собой адрес объекта данного типа в памяти программы, но также является специфическим типов, с которым можно производить определенные операции. В частности, указатели на объекты классов-наследников можно приводить к указателям на их базовые классы. Рассмотрим на примере, каким образом это делается.
Для этого определим функцию, проверяющую одну из аксиом-равенств АТД «стек», а именно, аксиому
Функция будет выглядеть так:
Данная функция получает в качестве параметра указатель на абстрактный тип Stack. В качестве этого параметра можно подставлять его реализации в класса-наследниках. Например:
Здесь работает принцип подстановки Лисков, т.е. вместо типа Stack* был подставлен тип ArrayStack*. Кроме того, благодаря тому, что методы базового класса объявлены как виртуальные, производится вызов методов класса-наследника ArrayStack, т.е. работает реализация АТД Stack, выполненная на основе массива.
В описанном примере используется встроенная в язык C++ возможность реализации абстрактных типов данных. При этом реализации АТД подставляются динамически, во время исполнения программы. Однако, в C++ также можно реализовать концепцию АТД по другому, используя механизм шаблонов и, таким образом, связывая АТД с его реализацией на этапе компиляции.
Механизм, реализующий эту возможность, называется в C++ «сuriously recurring template pattern» (CRTP) [8]. Для реализации статического (на этапе компиляции) полиморфизма эта концепция выглядит следующим образом:
В виде C++ кода это будет выглядеть следующем образом:
Для реализации АТД с помощью статического полиморфизма базовый шаблонный класс B реализует операции данного АТД, но вызывает при этом соответствующие методы класса-наследника, переданного классу B в качестве параметра шаблона. Приведем конкретный пример:
Это, фактически, спецификация операций абстрактного типа данных Stack. Каждая операция вызывает внутри себя операцию класса-параметра шаблона, представляющего реализацию данного абстрактного типа.