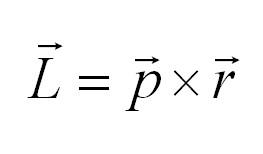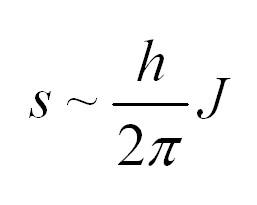Что такое спины электронов

28.10.202330.04.2022 admin 0 Comments

Что такое спин в физике: момент импульса, бозоны, фермионы

Итак, полностью абстрагируемся и забываем любые классические определения. Ибо спин – это понятие, присущее исключительно квантовому миру. Попробуем разобраться в том, что это такое.

Больше полезной информации для учащихся – у нас в телеграм.

Спин и момент импульса

Спин (от английского spin – вращаться) – собственный момент импульса элементарной частицы.

Теперь вспомним, что такое момент импульса в классической механике.

Момент импульса – это физическая величина, характеризующая вращательное движение, точнее, количество вращательного движения.

В классической механике момент импульса определяется как векторное произведение импульса частицы на ее радиус вектор:

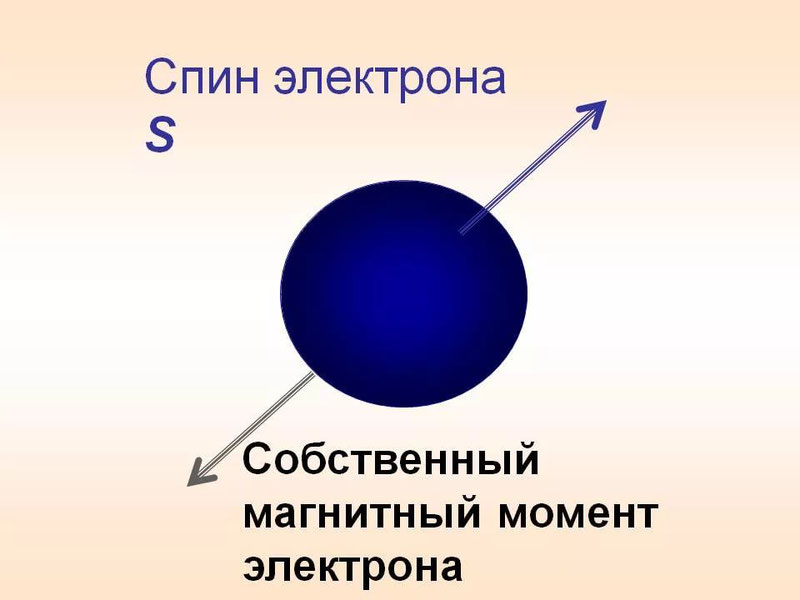
По аналогии с классической механикой спин характеризует вращение частиц. Их представляют в виде волчков, вращающихся вокруг оси. Если частица имеет заряд, то, вращаясь, она создает магнитный момент и явлеятся своего рода магнитом.

Однако данное вращение нельзя трактовать классически. Все частицы помимо спина обладают внешним или орбитальным моментом импульса, характеризующим вращение частицы относительно какой-то точки. Например, когда частица движется по круговой траектории (электрон вокруг ядра).

Спин же является собственным моментом импульса, то есть характеризует внутреннее вращательное состояние частицы вне зависимости от внешнего орбитального момента импульса. При этом спин не зависит от внешних перемещений частицы.

Представить, что же там вращается внутри частицы, невозможно. Однако факт остается фактом – для заряженных частиц с разнонаправленными спинами траектории движения в магнитном поле будут различны.

Спиновое квантовое число

Для характеристики спина в квантовой физике введено спиновое квантовое число.

Спиновое квантовое число – одно из квантовых чисел, присущих частицам. Часто спиновое квантовое число называют просто спином. Однако следует понимать, что спин частицы (в понимании собственного момента импульса) и спиновое квантовое число – это не одно и то же. Спиновое число обозначается буквой J и принимает ряд дискретных значений, а само значение спина пропорционально приведенной постоянной Планка:

Бозоны и фермионы

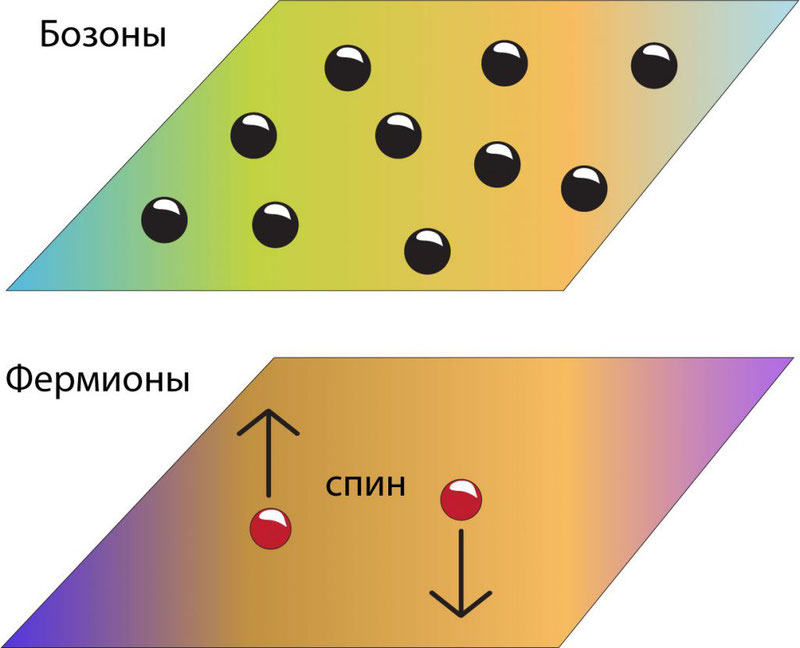
Разным частицам присущи разные спиновые числа. Так, главное отличие состоит в том, что одни обладают целым спином, а другие – полуцелым. Частицы обладающие целым спином называются бозонами, а полуцелым – фермионами.

Бозоны подчиняются статистике Бозе-Эйнштейна, а фермионы – Ферми-Дирака. В ансамбле частиц, состоящем из бозонов, любое их количество может находиться в одинаковом состоянии. С фермионами все наоборот – наличие двух тождественных фермионов в одной системе частиц невозможно.

Фермионы: электрон, лептон, кварк

Попробуем представить, чем отличаются частицы с разными спиновыми числами на примерах из макромира. Если спин объекта равен нулю, то его можно представить в виде точки. Со всех сторон, как ни вращай этот объект, он будет одинаков. При спине равном 1 поворот объекта на 360 градусов возвращает его в состояние, идентичное первоначальному состоянию.

Надеемся, что вы осилите эту теорию быстро и сможете при случае применить знания на практике. Ну а если задачка по квантовой механике оказалось непосильно сложной или не можете не забывайте о студенческом сервисе, специалисты которого готовы прийти на выручку. Учитывая, что сам Ричард Фейнман сказал, что «в полной мере квантовую физику не понимает никто», обратиться за помощью к опытным специалистам – вполне естественно!

Источник

# чтиво | Что такое спин?

После того, как мы выяснили, что такое абсолютный ноль и можно ли восстановить информацию о том, что ела черная дыра, на повестке дня появился еще один интересный вопрос. Вопрос сложный, поскольку лежит в области квантовой физики. Звучит он примерно так:

Что еще за спин?

Если вы думаете, что экспрессия была лишней, вы ошибаетесь. Спин — одна из тех странных вещей в квантовой механике, пытаясь понять которые, вы думаете, что интуиция и личный жизненный опыт вам помогут. Но это не так. Напротив, ваша интуиция более вероятно упадет на колени перед вами. Попробуйте не доверять ей.

Начнем с того, что у всех частиц есть фундаментальный спин. Спин — «ось» от английского spin. Так же, как электрический заряд или масса, спин помогает определить тип частицы.

Некоторые частицы, вроде электронов, позитронов и кварков (протоны и нейтроны состоят из кварков, также фундаментальных частиц Стандартной модели), обладают спином ½. Они известны как «фермионы». Другие, фотоны, глюоны, а также W- и Z-частицы, обладают спином 1. Они известны как «бозоны». Очевидно, фермионы и бозоны ведут себя по-разному.

Если все это время вы согласно кивали, тонкий голосок у вас в голове, наверное, говорил что-то типа «полспина чего?». Стоит отметить, к внутреннему голосу по-хорошему нужно прислушиваться, поэтому давайте поговорим о том, как работает спин электрона.

Это как маленький гироскоп, но не совсем.

Почему электроны? Потому что если вы поймете, что такое спин электрона, все остальное будет простым. Попробуйте представить, что электрон — это маленький гироскоп. Он вращается и вертится без остановки. Вне зависимости от того, что вы делаете с ним, вы не можете замедлить или ускорить вращение электрона; вы просто можете изменить его положение.

Что бы вы ни делали, у электрона всегда будет спин ½. Но ½ чего? Числа, известного как «приведенная постоянная Планка». Это очень маленькое число. Очень.

Вот вам первый странный факт. Обычно вы можете замедлить вращающееся тело. Супермен смог остановить вращение Земли, например.

С другой стороны, мы имеем дело с маленьким вращающимся гироскопом. Угловой момент — это одна из тех постоянных величин, которые сводят с ума физиков. При изменении направления спина электрона, угловой момент передается куда угодно — от орбиты до другого электрона.

Поскольку у электрона есть заряд, и поскольку он «вращается по оси», он создает небольшое магнитное поле. Так работает любой электромагнит. Мы можем обнаружить магнитное поле электрона или отклонить отдельные электроны, используя другие магниты, чтобы выяснить, в каком направлении вращается электрон. Но…

Магнитное поле работает совсем не так.

Возьмите маленький заряженный шарик и закрутите его вокруг оси. Вы создадите магнит. Вне зависимости от того, насколько велик или мал шар, оказывается, что магнитное поле будет точно предсказано кратным угловым моментом. Есть куча констант, связанных с зарядом и массой шарика, но не с размером.

Проблема в том, что если представить электрон таким же образом, описанная выше процедура не прокатит вообще. Магнитное поле будет в два раза больше. Точнее, в 2,0023193044 раза. Это число измерено с безумным уровнем точности и вычислено теоретически. В игру вступает эта чертова «квантовая теория поля», потому что мы можем сделать несколько точных предсказаний.

Странный факт номер два: вы не можете, не имеете права думать об электроне, как о маленькой микроскопической заряженной сфере. Просто получатся неправильные цифры.

Хотя у электронов есть фиксированный спин, вы можете предположить, что компоненты спина в определенном направлении могут принимать любое старое значение, которое нам нравится. Подумайте об этом в следующем примере. Допустим, у меня была метровая палка (длиной в 1 метр), одним концом воткнутая в землю под углом. Вы можете измерить высоту от верхнего конца до земли, и в зависимости от угла, получите значение между 0 и 1 метром.

Вы знаете, что Земля вращается, но если вы когда-нибудь видели глобус, вы в курсе, что он наклонен где-то под углом 23 с половиной градуса по отношению к плоскости орбиты. Другими словами, если вы измерите «ось» (или спин) Земли сверху донизу, вы получите меньше, чем полную длину оси. Ось представляется немного расшатанной из стороны в сторону.

С электронами такое не работает. Если вы создали небольшое магнитное поле, чтобы различить их, вы выясните, что отдельный электрон в 100 % случаев вертится вверх и в 100 % случаев вертится вниз, в зависимости от случая, и никогда — между. Что более странно, не имеет значения, как вы будете настраивать свою измерительную аппаратуру, вы всегда придете к одному и тому же начальному результату: либо одна сторона, либо другая, третьего не дано.

И здесь у нас рождается третий странный факт. Предположим, вы измеряете электрон и выясняете, что он обладает верхним спином. После вы пытаетесь измерить спин слева-направо. Здравый смысл подскажет вам, что число будет равно нулю, так как вы знаете, что электрон вертится снизу вверх, а не слева направо. Но как мы отмечали выше, здравый смысл вам не поможет. Выясняется, что: а) в половине случаев, когда вы измеряете электрон, он будет «слева», в половине — «справа», и б) право и лево определяется абсолютной случайностью. Правда. Ничто во вселенной не сможет сказать вам, какую сторону выберет электрон. Такого рода случайность сильно огорчала Эйнштейна (вспомните его высказывание о том, что Бог не играет в кости).

Вам нужно дважды повернуть электрон, чтобы он выглядел, «как прежде»

Это четвертый странный факт. Вам нужно дважды повернуть электрон вокруг оси, и он будет выглядеть так же, как и в начале.

Тот же эффект возникнет, если вы представите, будто подменяете один электрон другим. Ничего не меняется, только появляется знак минус перед всей волновой функцией. Кажется незначительным, пока вы не поймете, что…

Знак минус — это то, что делает вас возможным.

Другой способ сказать это: электроны (и все фермионы: кварки, позитроны, нейтрино и т.д.) не могут находиться в одном и том же месте с одним и тем же спином. Это знаменитый «запрет Паули». Он предсказывает, что электроны в атомах не могут быть в одном и том же состоянии, но вместе этого занимают разные орбитали. Если бы все было не так, электроны занимали бы самые низкие уровни, и элементы вели бы себя скучновато, как водород. Скучно и не способствует зарождению жизни.

Бозоны, другой тип частиц, не работают по этому принципу. Поменяйте местами два бозона, и ничего не изменится. Поверните бозон единожды, и все вернется в нормальное русло. У них спин равен одному, что означает только то, что они ведут себя точно так, как вы ожидаете. Но таковы лишь бозоны, обнаруженные на сегодняшний день. У бозона Хиггса (если он существует) спин 0, у гравитона (если он существует) спин 2, но мы пока можем о них не говорить. Бозоны могут находиться в одном месте и обладать одним и тем же спином. Вот почему мы можем получить конденсат Бозе-Эйнштейна, который представляет собой кучу бозонов в одном состоянии.

«Фишка» не в том, что спин — странная штука, хотя с этим никто не спорит. «Фишка» в том, что спин лежит в центре куда более серьезных и фундаментальных вещей, в основе их работы, чем вы можете подозревать.

Источник

Что такое спины электронов

В 1922 году немецкие физики О. Штерн и В. Герлах поставили опыты, целью которых было измерение магнитных моментов P_m атомов различных химических элементов. Для химических элементов, образующих первую группу таблицы Менделеева и имеющих один валентный электрон, магнитный момент атома равен магнитному моменту валентного электрона, т.е. одного электрона.

Идея опыта заключалась в измерении силы, действующей на атом в сильно неоднородном магнитном поле. Неоднородность магнитного поля должна быть такова, чтобы она сказывалась на расстояниях порядка размера атома. Только при этом можно было получить силу, действующую на каждый атом в отдельности.

Схема опыта изображена на рис. 7.9. В колбе с вакуумом, 10 –5 мм рт. ст., нагревался серебряный шарик К, до температуры испарения.

Атомы серебра летели с тепловой скоростью около 100 м/с через щелевые диафрагмы В и, проходя резко неоднородное магнитное поле, попадали на фотопластинку А.

Если бы момент импульса атома (и его магнитный момент ) мог принимать произвольные ориентации в пространстве (т.е. в магнитном поле), то можно было ожидать непрерывного распределения попаданий атомов серебра на фотопластинку с большой плотностью попаданий в середине. Но на опыте были получены совершенно неожиданные результаты: на фотопластинке получились две резкие полосы – все атомы отклонялись в магнитном поле двояким образом, соответствующим лишь двум возможным ориентациям магнитного момента (рис. 7.10).

Этим доказывался квантовый характер магнитных моментов электронов. Количественный анализ показал, что проекция магнитного момента электрона равна магнетону Бора:

Таким образом, для атомов серебра Штерн и Герлах получили, что проекция магнитного момента атома (электрона) на направление магнитного поля численно равна магнетону Бора.

Опыты Штерна и Герлаха не только подтвердили пространственное квантование моментов импульсов в магнитном поле, но и дали экспериментальное подтверждение тому, что магнитные моменты электронов тоже состоят из некоторого числа «элементарных моментов», т.е. имеют дискретную природу. Единицей измерения магнитных моментов электронов и атомов является магнетон Бора (ħ – единица измерения механического момента импульса).

Кроме того, в этих опытах было обнаружено новое явление. Валентный электрон в основном состоянии атома серебра имеет орбитальное квантовое число l = 0 (s—состояние). Но при l = 0 (проекция момента импульса на направление внешнего поля равна нулю). Возник вопрос, пространственное квантование какого момента импульса обнаружилось в этих опытах и проекция какого магнитного момента равна магнетону Бора.

В 1925 г. студенты Геттингенского университета Гаудсмит и Уленбек предположили существование собственного механического момента импульса у электрона (спина) и, соответственно, собственного магнитного момента электрона Pms.

Введение понятия спина сразу объяснило ряд затруднений, имевшихся к тому времени в квантовой механике. И в первую очередь – результатов опытов Штерна и Герлаха.

Авторы дали такое толкование спина: электрон – вращающийся волчок. Но тогда следует, что «поверхность» волчка (электрона) должна вращаться с линейной скоростью, равной 300 с, где с – скорость света. От такого толкования спина пришлось отказаться.

В современном представлении – спин, как заряд и масса, есть свойство электрона.

П. Дирак впоследствии показал, что существование спина вытекает из решения релятивистского волнового уравнения Шредингера.

Из общих выводов квантовой механики следует, что спин должен быть квантован: , где s – спиновое квантовое число.

Аналогично, проекция спина на ось z (L_sz) (ось z совпадает с направлением внешнего магнитного поля) должна быть квантована и вектор может иметь (2s + 1) различных ориентаций в магнитном поле.

Из опытов Штерна и Герлаха следует, что таких ориентаций всего две: , а значит s = 1/2, т.е. спиновое квантовое число имеет только одно значение.

Для атомов первой группы, валентный электрон которых находится в s—состоянии (l = 0), момент импульса атома равен спину валентного электрона. Поэтому обнаруженное для таких атомов пространственное квантование момента импульса в магнитном поле является доказательством наличия у спина лишь двух ориентаций во внешнем поле. (Опыты с электронами в p—состоянии подтвердили этот вывод, хотя картина получилась более сложной) (желтая линия натрия – дуплет из-за наличия спина).

Численное значение спина электрона:

По аналогии с пространственным квантованием орбитального момента проекция спина квантуется (аналогично, как , то и ). Проекция спина на направление внешнего магнитного поля, являясь квантовой величиной, определяется выражением: