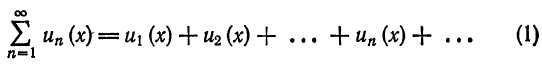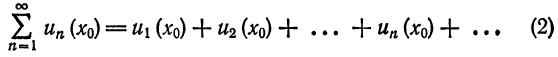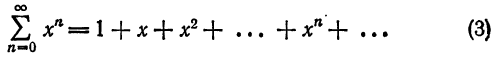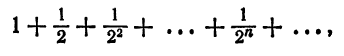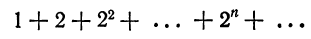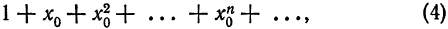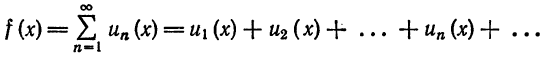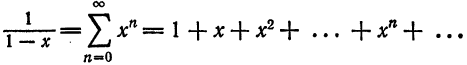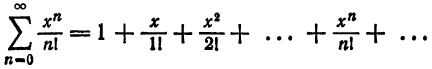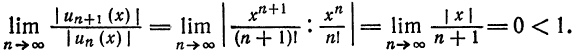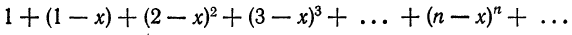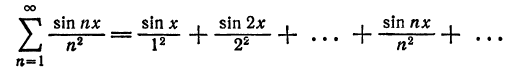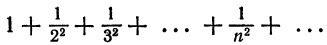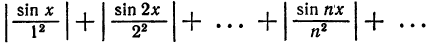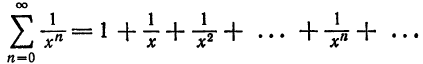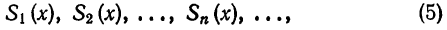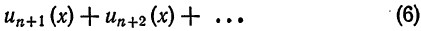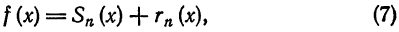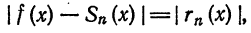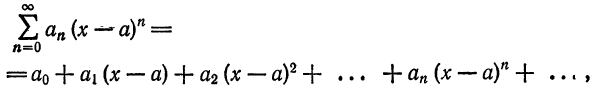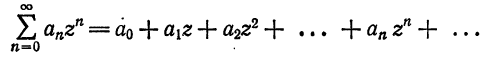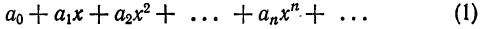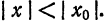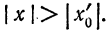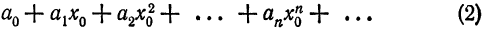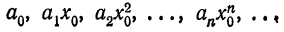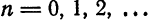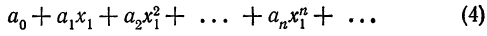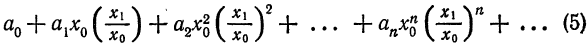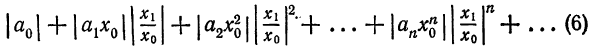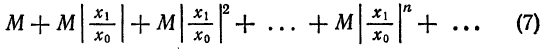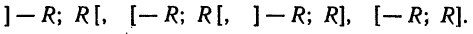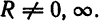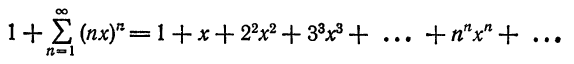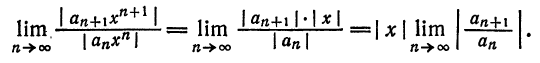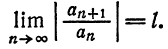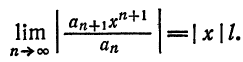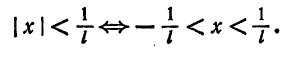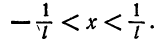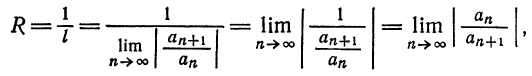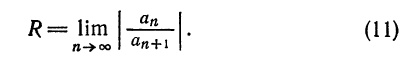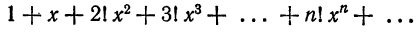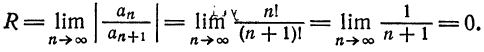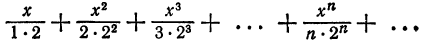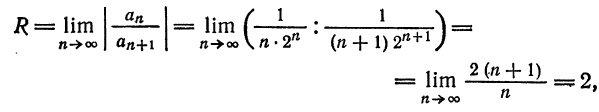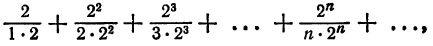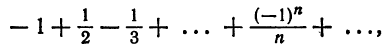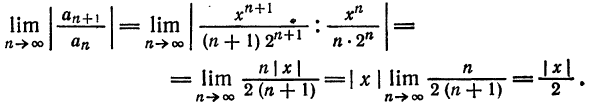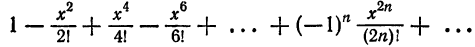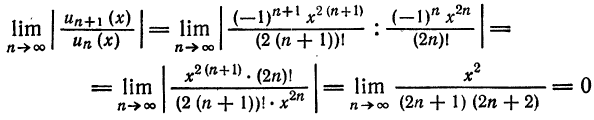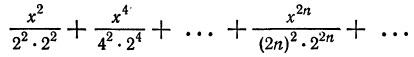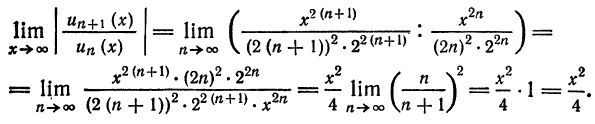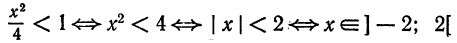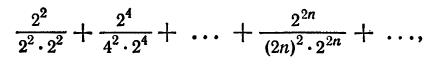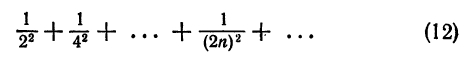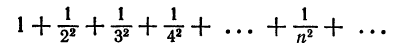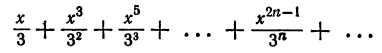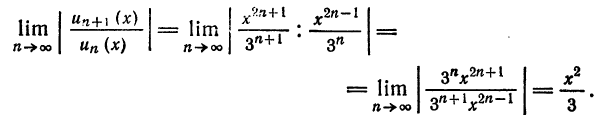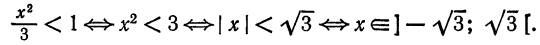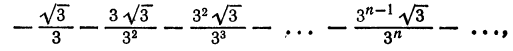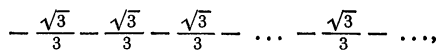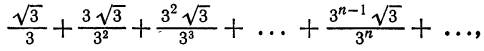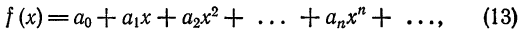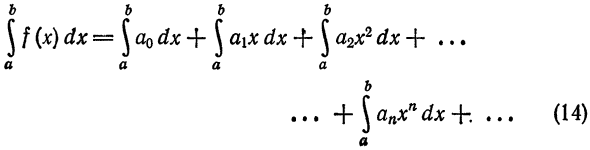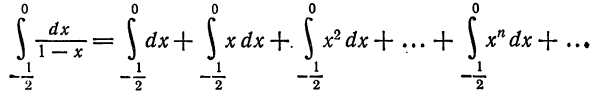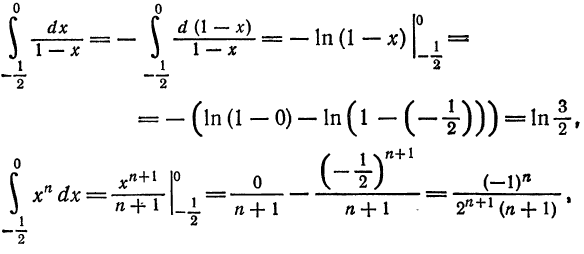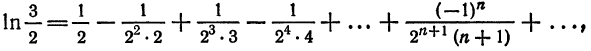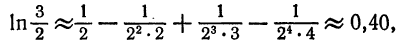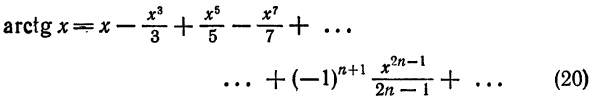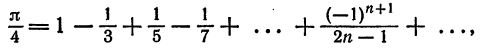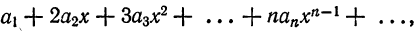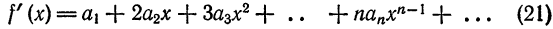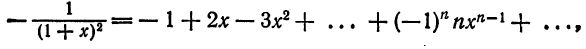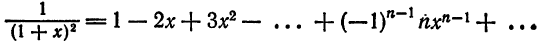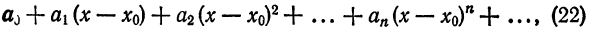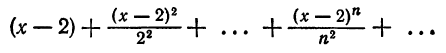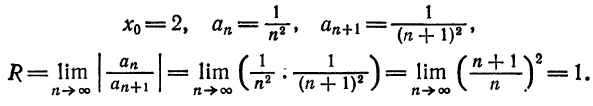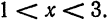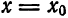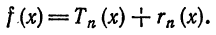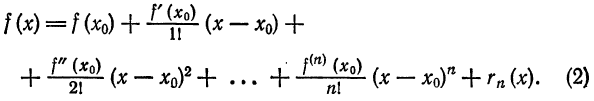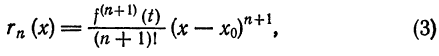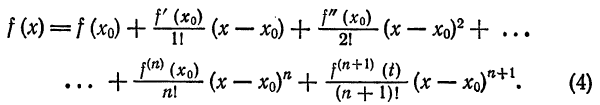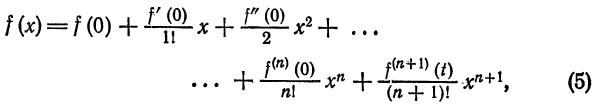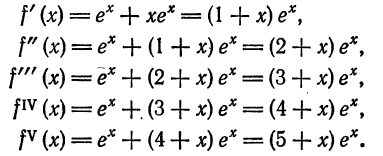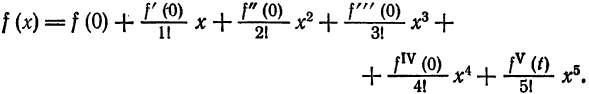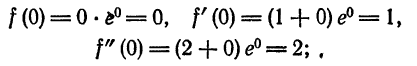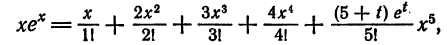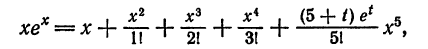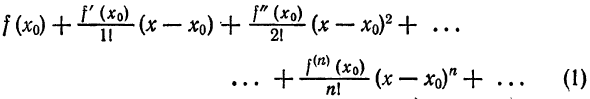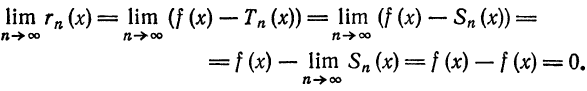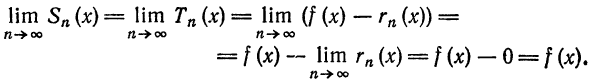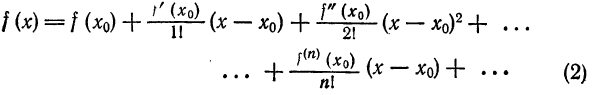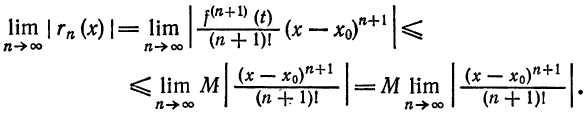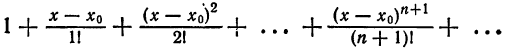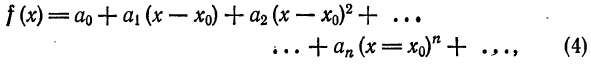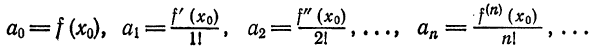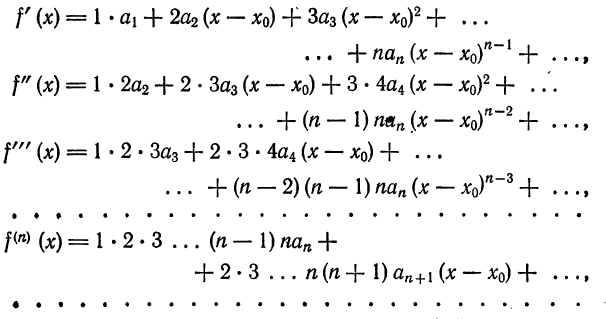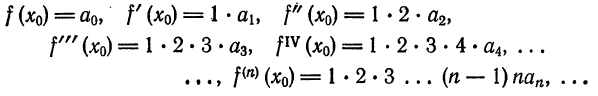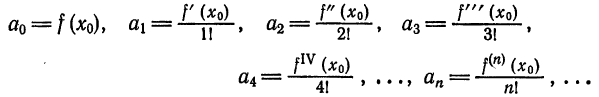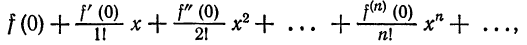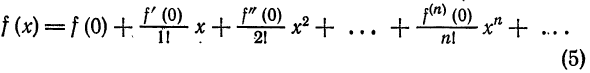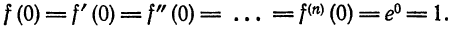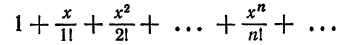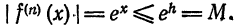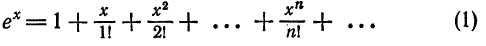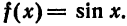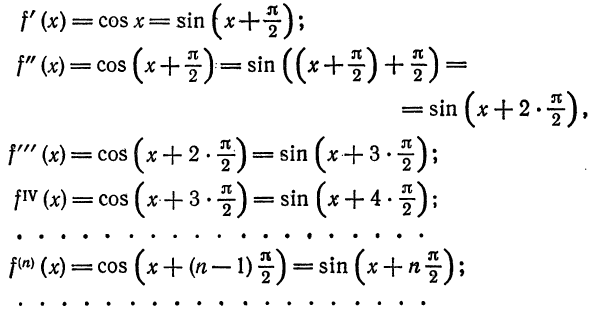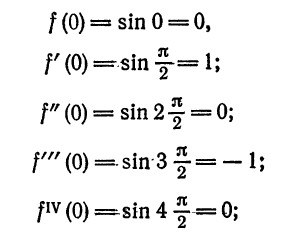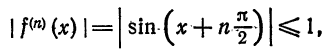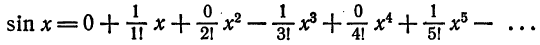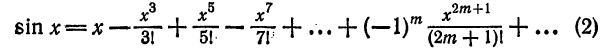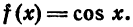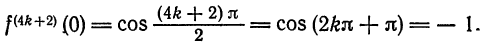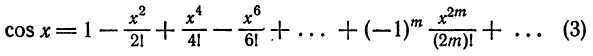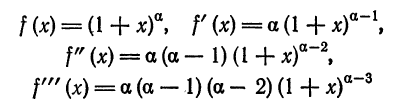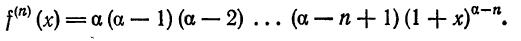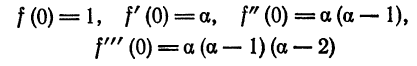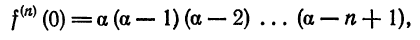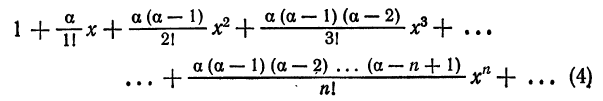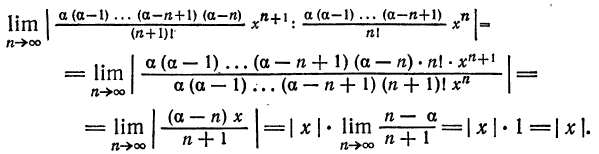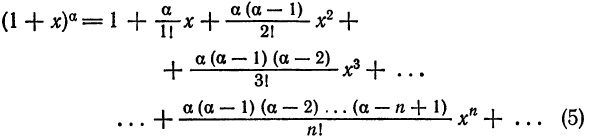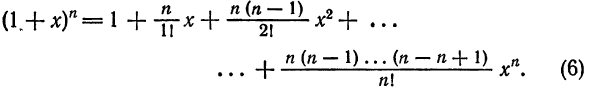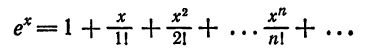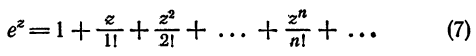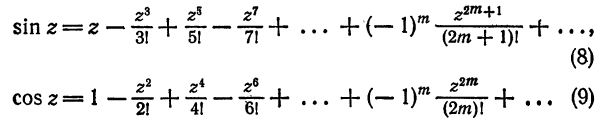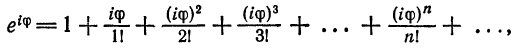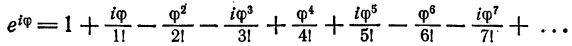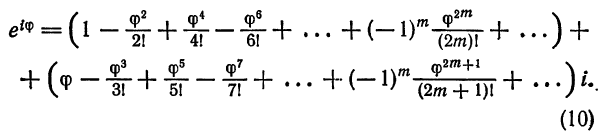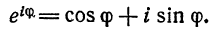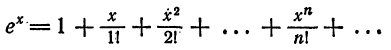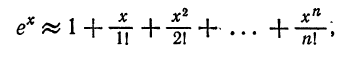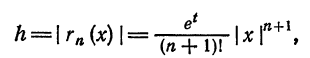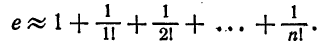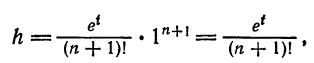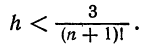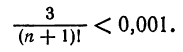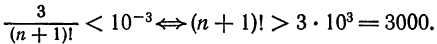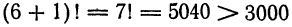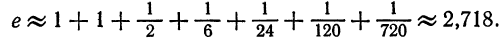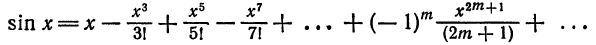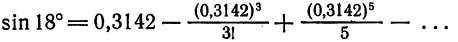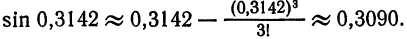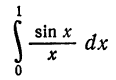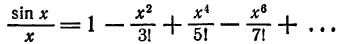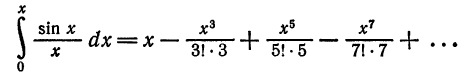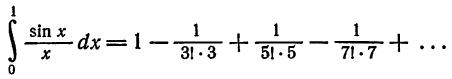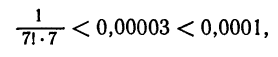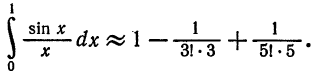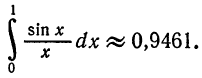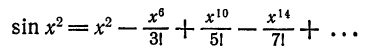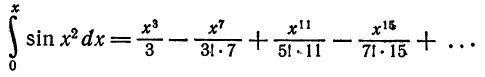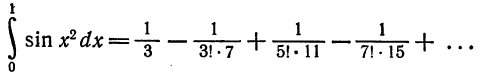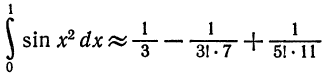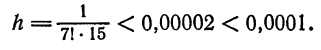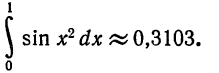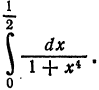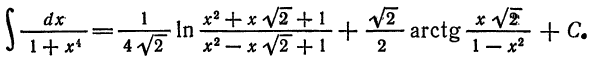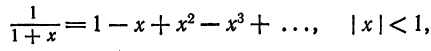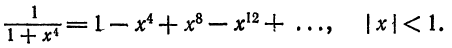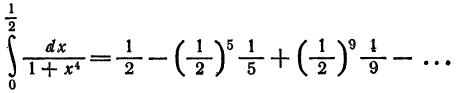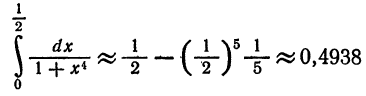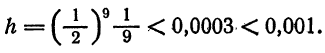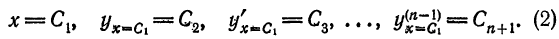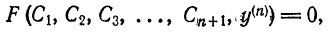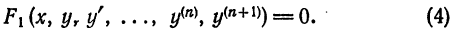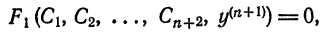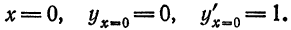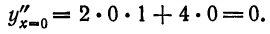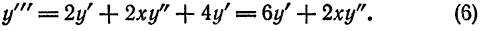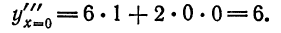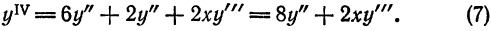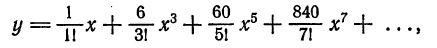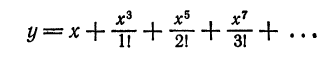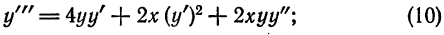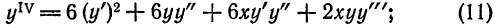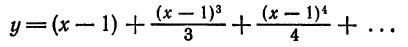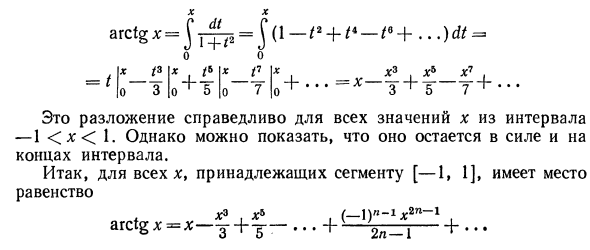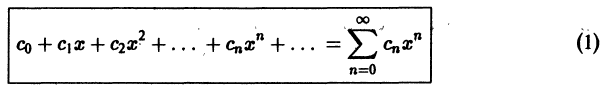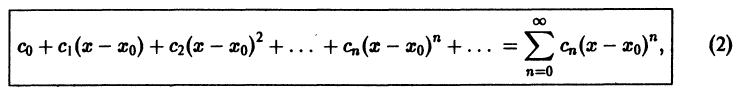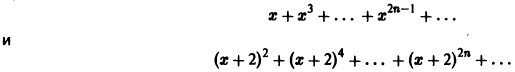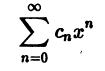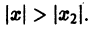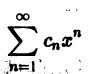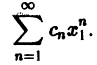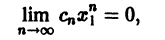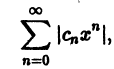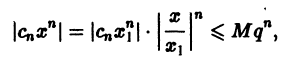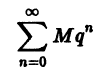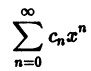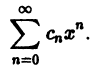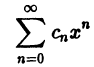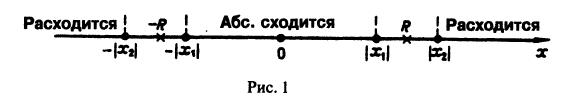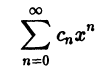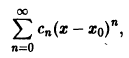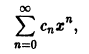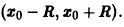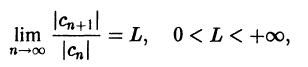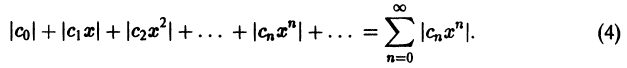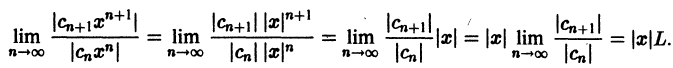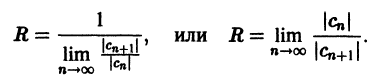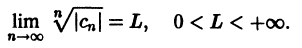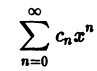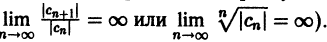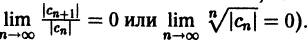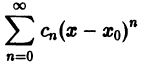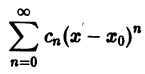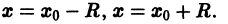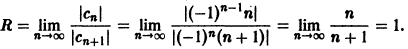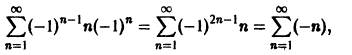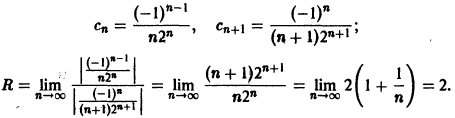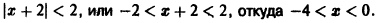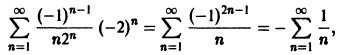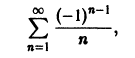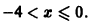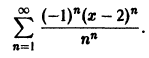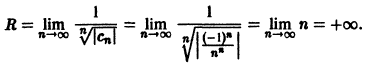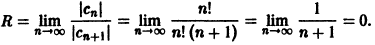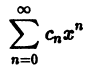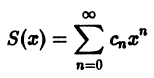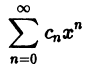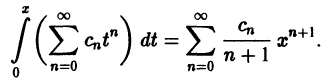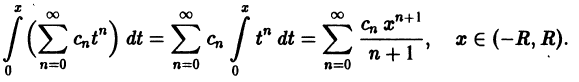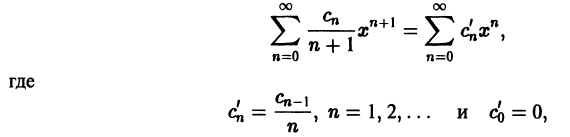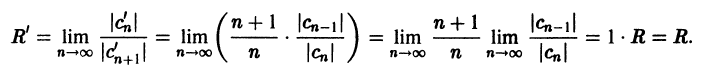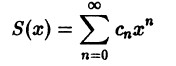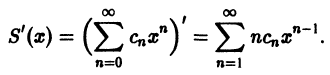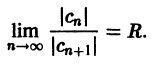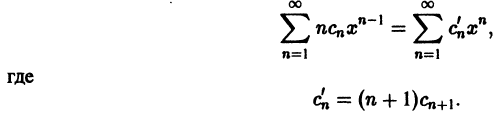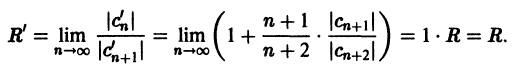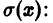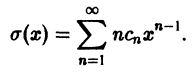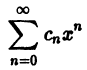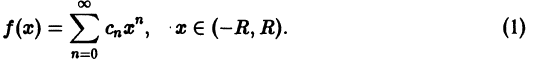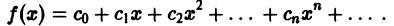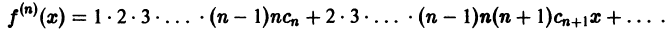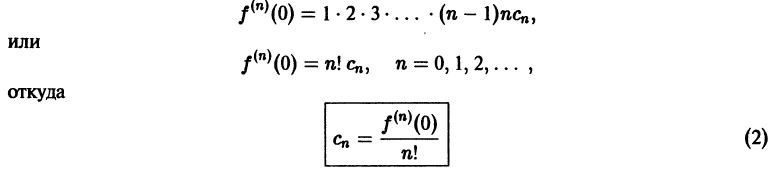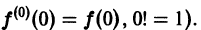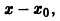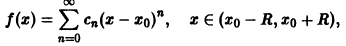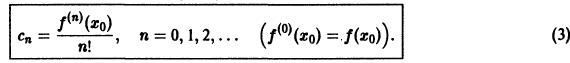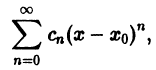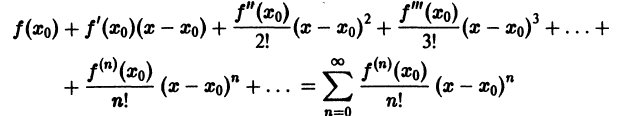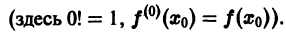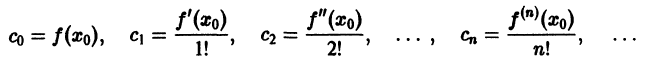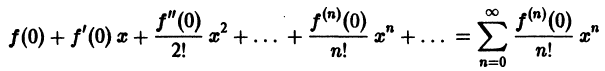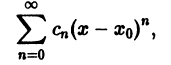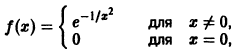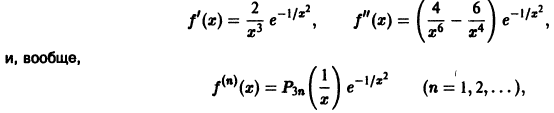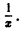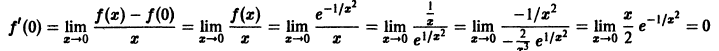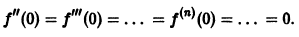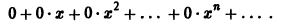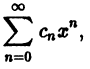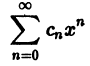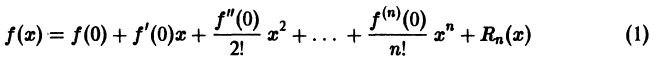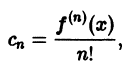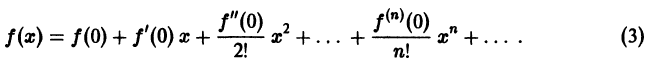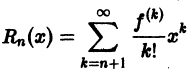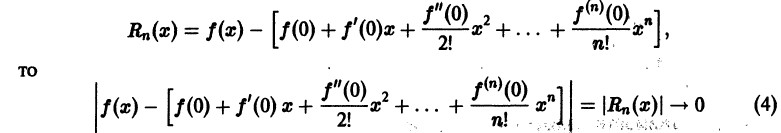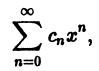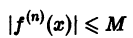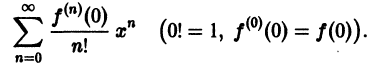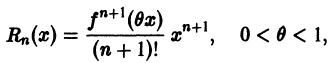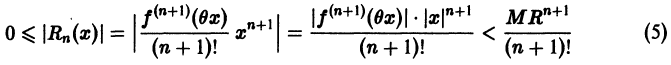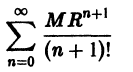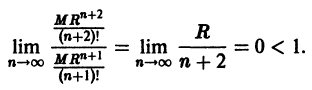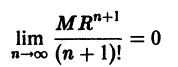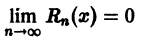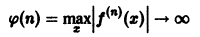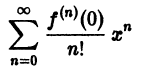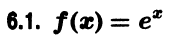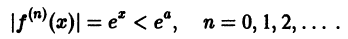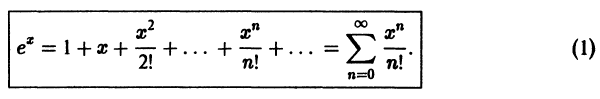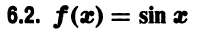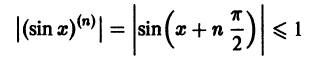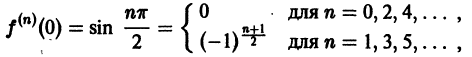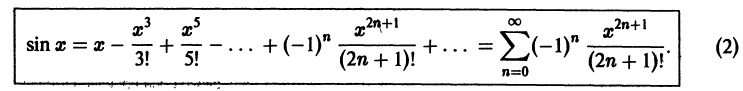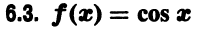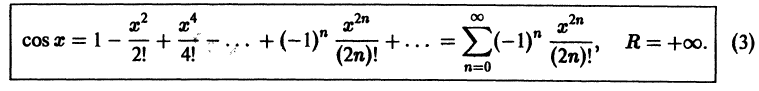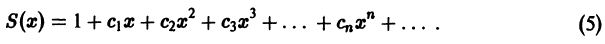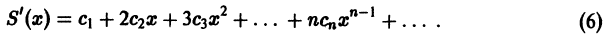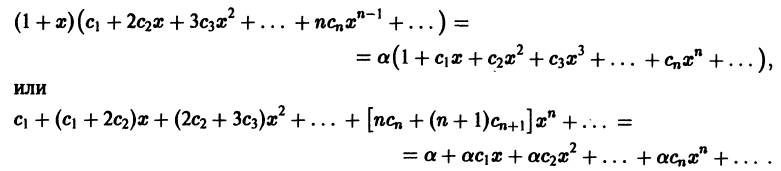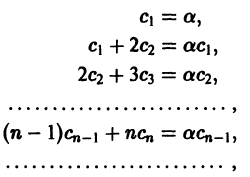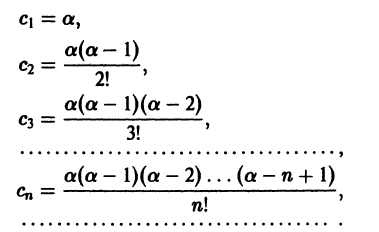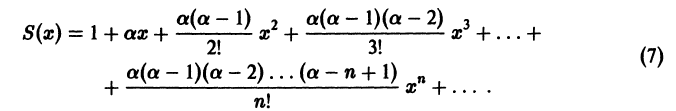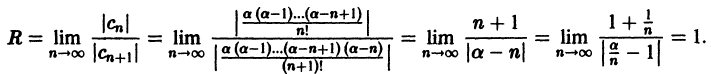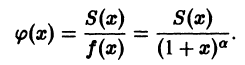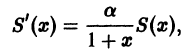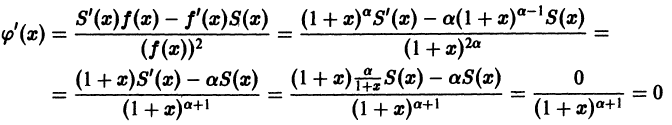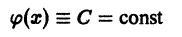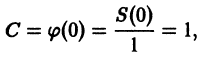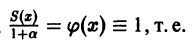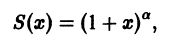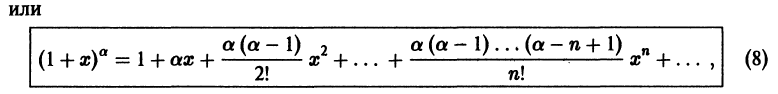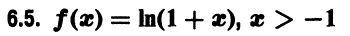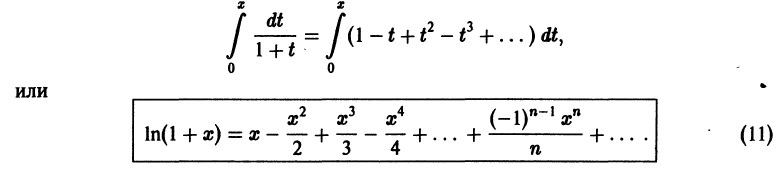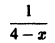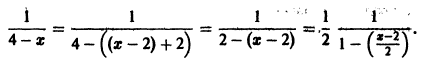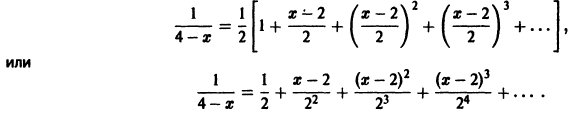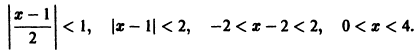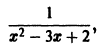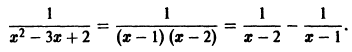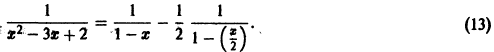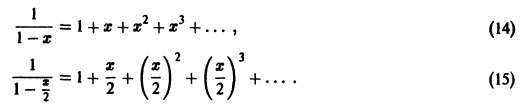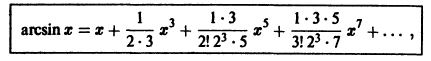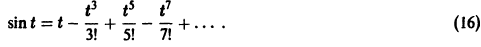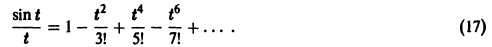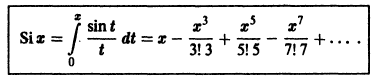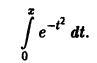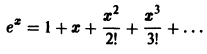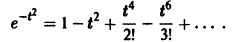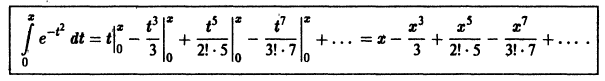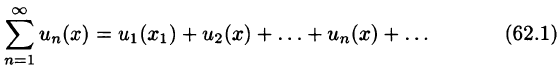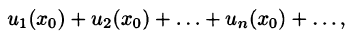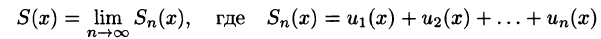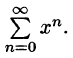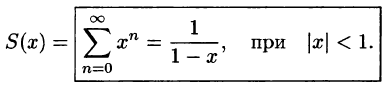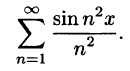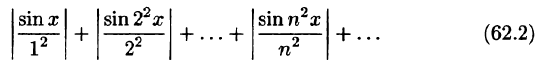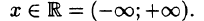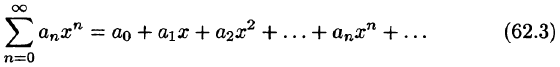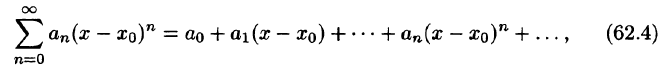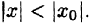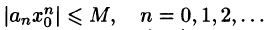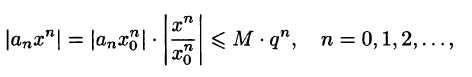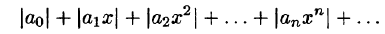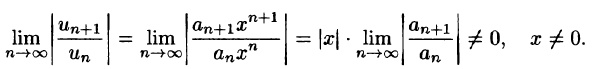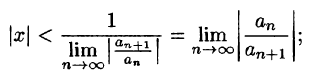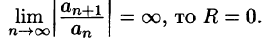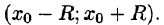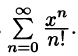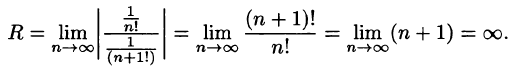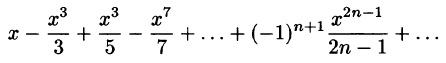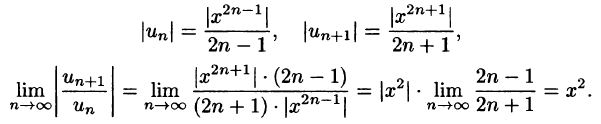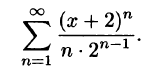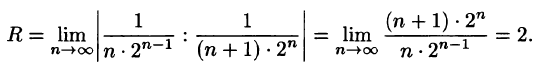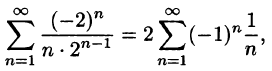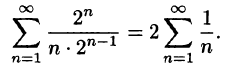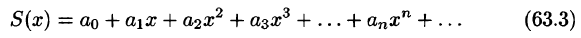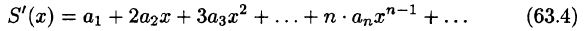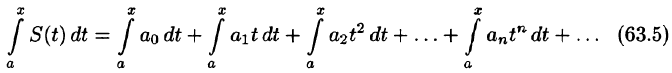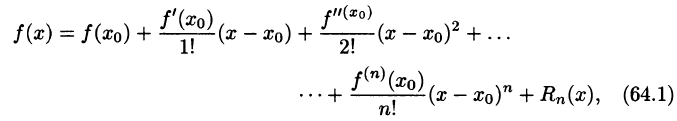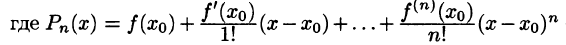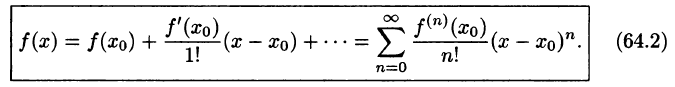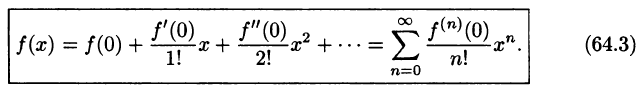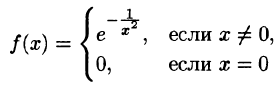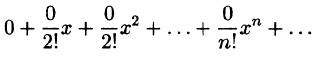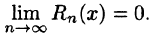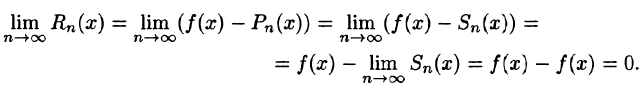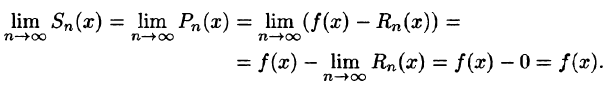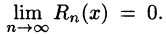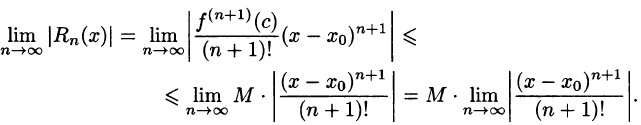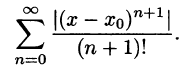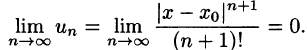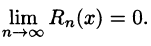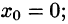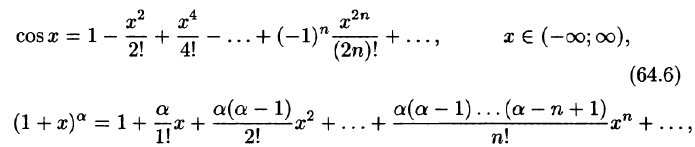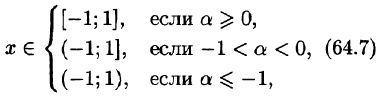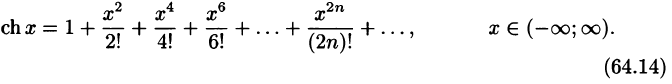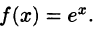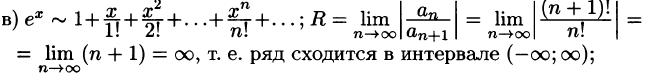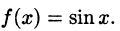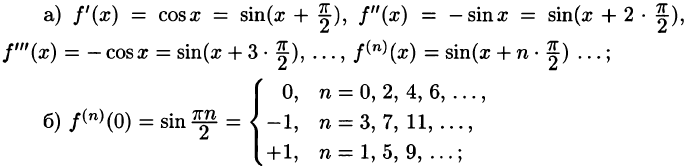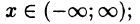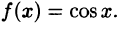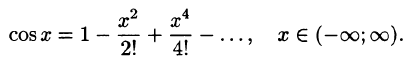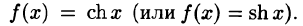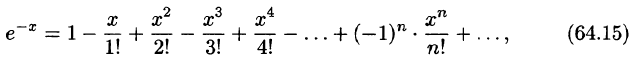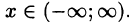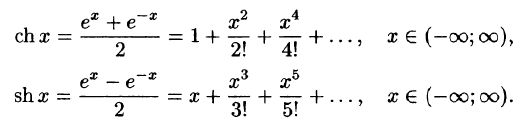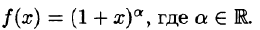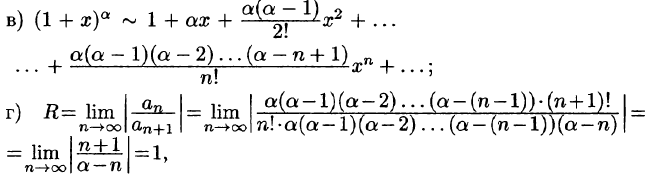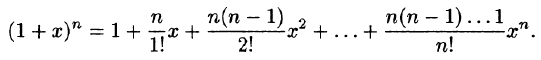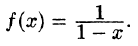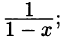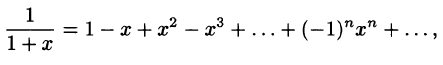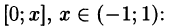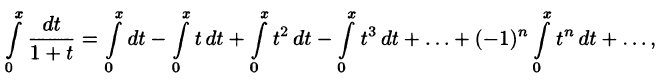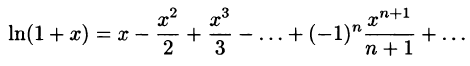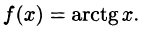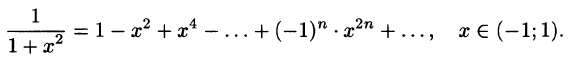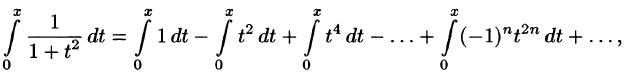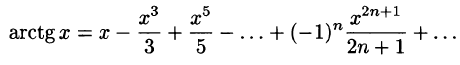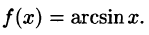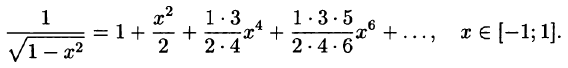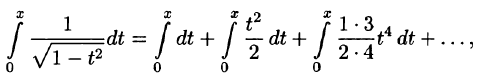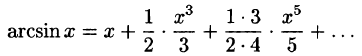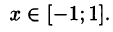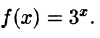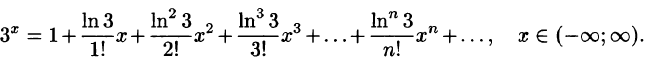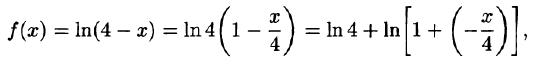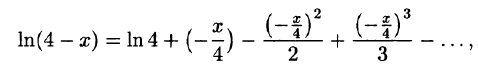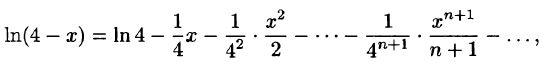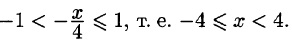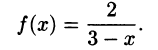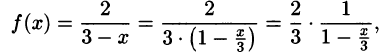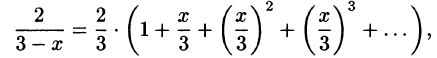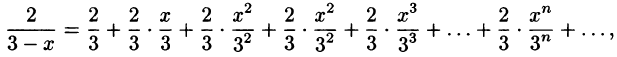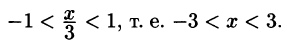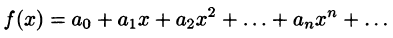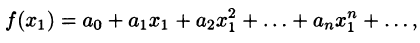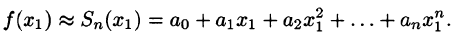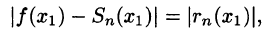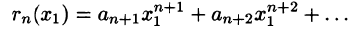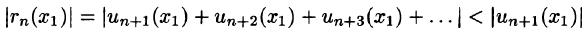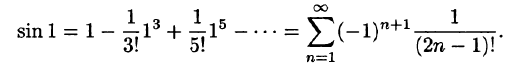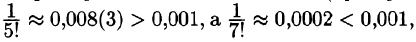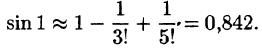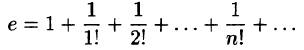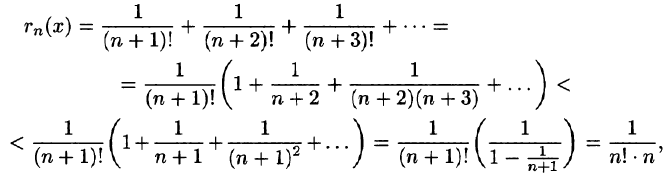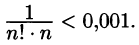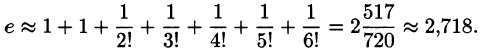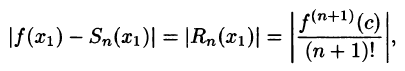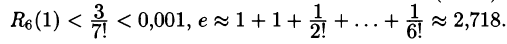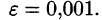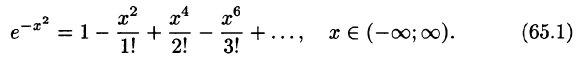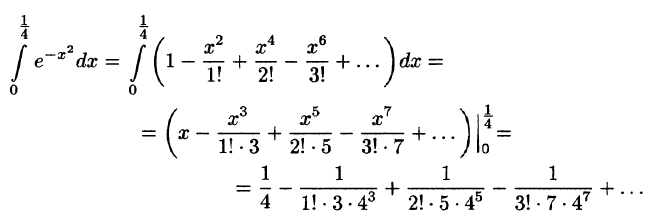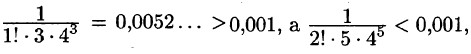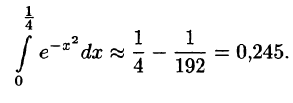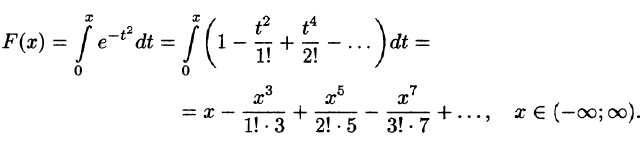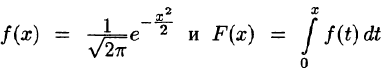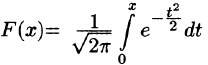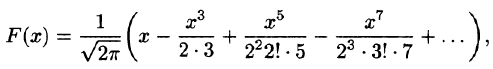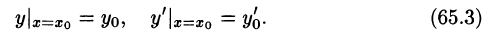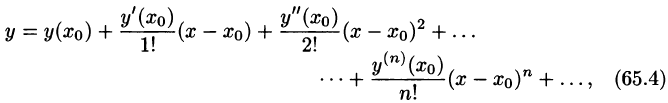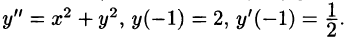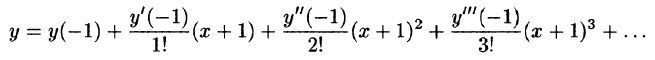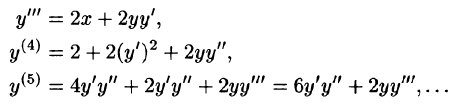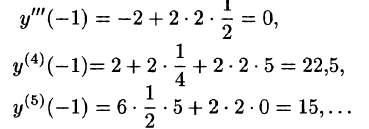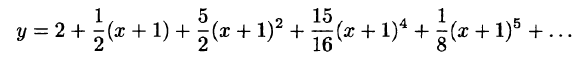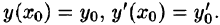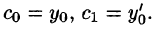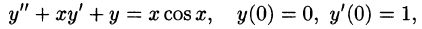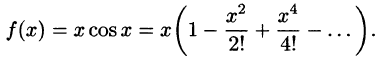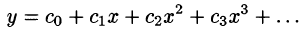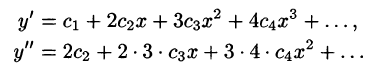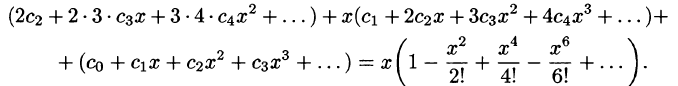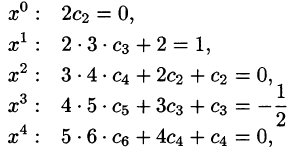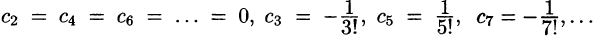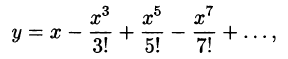Что такое способ рядов

Что такое способ рядов

1. Загадки природы и тайны быта

Вот говорят: «Толщиной с человеческий волос». А какова она – толщина волоса? Можно ли её измерить? Или, как говорят физики, оценить, в том случае, если измерения нельзя выполнить с высокой точностью. Или, допустим, можно ли измерить толщину нитки?

2. Другие х – файлы

Возможны и другие задачи. Можно ли обычной линейкой измерить:

а) толщину страницы учебника;

б) диаметр горошины или пшена;

в) толщину тонкой проволоки?

Смотрите об этом презентацию и при затруднениях читайте текст.

Не поискать ли мне тропы иной,

Приёмов новых, сочетаний странных?

Шекспир справедливо отметил, что когда наши познания и житейский опыт не могут решить наши проблемы, надо искать другие способы решения. Как правило, какой-нибудь метод, да и отыщется!

3. А мне это надо?

А мне это надо? – спросите Вы. Как знать? Допустим, для шитья используются нитки разной толщины. Она указывается номером на катушке. Причём нитки №10 толще, чем нитки №20.

Для изготовления некоторых элементов электрической цепи необходимо знать толщину проволоки. Для печати книг, газет и журналов используется бумага разной толщины.

А ещё надо просто научиться решать практические задачи, чтобы получать хорошие отметки и сдать экзамен по физике.

4. Истина где-то рядом

Прямые измерения размеров малых или тонких тел невозможны по той причине, что измеряемые величины соизмеримы или даже меньше цены деления используемого прибора. Одним из способов измерения размеров малых тел является, так называемый, метод рядов. Этот метод основан на принципе суммирования длин (масс, объёмов) одинаковых элементов, образующих тело в целом.

Высота стопки одинаковых книг равна сумме высот отдельных книг в этой стопке: h = n · h₀

Толщина (высота) одной книги, в этом случае, равна: h₀ = h : n

Где: n – кол-во книг; h₀ — высота одной книги.

Задача 1. Определить диаметр шарика (бусины).

Обозначим диаметр буквой d . Это и будет размером малого тела, то есть его наибольшей шириной.

Сложность этой задачи заключается в размерах тел, которые такого же порядка, как и цена деления линейки. Диаметр шариков составляет несколько миллиметров и цена деления 1 мм. Это значит, что погрешность такого измерения очень большая. В этом случае лучше применить не прямое измерение диаметра шарика, а косвенное, с использованием метода рядов.

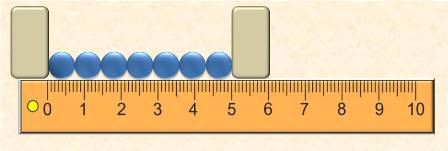
В ряд укладываем несколько шариков. Измеряем длину ряда линейкой и делим её на количество шариков в ряду. Точность косвенных измерений диаметра шарика при таком способе будет значительно выше, чем при прямом измерении линейкой.

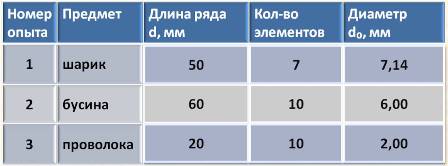
Длина ряда: l = 5 см = 50 мм Количество шариков в ряду: n = 7

Задача 2. Найти диаметр бусины на нитке.

В этом случае задача упрощается. Достаточно плотно сдвинуть некоторое количество бусин на нитке. Расположить этот участок нити вдоль линейки. А затем выполнить прямые и косвенные измерения.

Длина участка нити: l = 6 см = 60 мм Количество бусин: n = 10

Задача 3. Определить диаметр тонкой проволоки.

Для решения этой задачи достаточно взять карандаш и намотать на него некоторое количество витков проволоки. Дальнейшие измерения и вычисления аналогичны.

Длина ряда из витков: l = 2 см = 20 мм Количество витков: n = 10

Оформление результатов

Результаты измерений лучше представлять в виде таблицы. Это удобно для косвенных измерений. А также в случае проведения однотипных измерений для разных тел.

Результаты измерений могут быть и такого вида: 6,00 мм. Такой вид записи показывает, что вычисления также выполнены с точностью до сотых. А число либо разделилось без остатка, и дольных значений нет, либо остаток меньшего порядка (тысячные, десятитысячные и т.д.).

Окончательная запись результатов в системе СИ:

С учётом погрешности:

Погрешность измерений будет уже не 0,5 мм, а в 7 (0,07 мм) и 10 (0,05 мм) раз меньше. И чем больше малых элементов в ряду, тем меньше погрешность измерений.

5. Территория экспериментов

Теперь можно решать практические задачи. В отличие от лабораторных работ, практические задачи не содержат указаний и бланк отчёта необходимо приготовить самому учащемуся. Примеры практических задач:

1. Определить толщину листа учебника физики.

2. Определить толщину нитки в катушке.

3. Определить объём одной капли воды.

Для оформления отчёта одной таблицы мало, надо знать Как составить отчёт по практической работе.

В презентации к уроку есть пример решения задачи и задание для рефлексии.

Источник

Измерение размеров малых тел методом рядов

Метод рядов используют для измерения размеров тел в случае, когда эти размеры меньше цены деления измерительного инструмента. Например, невозможно измерить толщину листа бумаги с помощью линейки с милли­метровыми делениями. Однако если измерить толщину пачки L, содержащей достаточно большое число N таких листов, и разделить полученную величи­ну на N, то мы определим среднюю толщину листа в пачке.

Данным способом можно измерить, например, диаметр тонкой проволоки, крупинок пшена и других малых тел.

1. Увеличивается или уменьшается точность измерения при увеличении числа предметов в ряду?

2. Как изменится максимальная абсолютная погрешность измерения сред­него диаметра тела: а) при увеличении числа тел в ряду в 10 раз; б) при уменьшении числа тел в ряду в 2 раза?

· Ознакомьтесь с критериями оценивания лабораторной работы на стр. 2-3 данного файла.

· Определите размер тел методом рядов. Проведённый эксперимент оформите в тетради для лабораторных работ в соответствии с образцом (памяткой).

Источник

Числовые ряды: определения, свойства, признаки сходимости, примеры, решения

Данная статья представляет собой структурированную и подробную информацию, которая может пригодиться во время разбора упражнений и задач. Мы рассмотрим тему числовых рядов.

Данная статья начинается с основных определений и понятий. Далее мы стандартные варианты и изучим основные формулы. Для того, чтобы закрепить материал, в статье приведены основные примеры и задачи.

Базовые тезисы

a k является общим или k –ым членом ряда.

Определения, рассмотренные выше, помогут вам для решения большинства примеров и задач.

Для того, чтобы дополнить определения, необходимо доказать определенные уравнения.

Мы доказали, что числовой ряд сходится.

Мы доказали, что числовой ряд расходится.

Ряд ∑ k = 1 ∞ b k знакопеременный, так как в нем множество чисел, отрицательных и положительных.

Второй вариант ряд – это частный случай третьего варианта.

Приведем примеры для каждого случая соответственно:

Для третьего варианта также можно определить абсолютную и условную сходимость.

Знакочередующийся ряд ∑ k = 1 ∞ b k абсолютно сходится в том случае, когда ∑ k = 1 ∞ b k также считается сходящимся.

Подробно разберем несколько характерных вариантов

Знакопеременный ряд ∑ k = 1 ∞ b k считается условно сходящимся в том случае, если ∑ k = 1 ∞ b k – расходящийся, а ряд ∑ k = 1 ∞ b k считается сходящимся.

Особенности сходящихся рядов

Проанализируем свойства для определенных случаев

Разложим исходный вариант:

Необходимое условие для определения, является ли ряд сходящимся

Проверим исходное выражение на выполнение условия lim n → + ∞ n 2 1 + n = lim n → + ∞ n 2 n 2 1 n 2 + 1 n = lim n → + ∞ 1 1 n 2 + 1 n = 1 + 0 + 0 = + ∞ ≠ 0

Как определить сходимость знакоположительного ряда.

Если постоянно пользоваться указанными признаками, придется постоянно вычислять пределы. Данный раздел поможет избежать сложностей во время решения примеров и задач. Для того, чтобы определить сходимость знакоположительного ряда, существует определенное условие.

Как сравнивать ряды

Существует несколько признаков сравнения рядов. Мы сравниваем ряд, сходимость которого предлагается определить, с тем рядом, сходимость которого известна.

Первый признак

Для того, чтобы закрепить полученный материал, детально рассмотрим пару типичных вариантов.

Второй признак

Согласно второму признаку можно определить, что сходящийся ряд ∑ k = 1 ∞ 1 k 3 означается, что первоначальный вариант также сходится.

Согласно приведенным выше тезисам, расходящийся ряд влечет собой расходимость исходного ряда.

Третий признак

Рассмотрим третий признак сравнения.

Признак Даламбера

Признак Даламбера справедлив в том случае, если предел бесконечен.

Определить, является ряд сходящимся или расходящимся ∑ k = 1 ∞ 2 k + 1 2 k по признаку Даламбера.

Необходимо проверить, выполняется ли необходимое условие сходимости. Вычислим предел, воспользовавшись правилом Лопиталя: lim k → + ∞ 2 k + 1 2 k = » open=» ∞ ∞ = lim k → + ∞ 2 k + 1 ‘ 2 k ‘ = lim k → + ∞ 2 2 k · ln 2 = 2 + ∞ · ln 2 = 0

Мы можем увидеть, что условие выполняется. Воспользуемся признаком Даламбера: lim k → + ∞ = lim k → + ∞ 2 ( k + 1 ) + 1 2 k + 1 2 k + 1 2 k = 1 2 lim k → + ∞ 2 k + 3 2 k + 1 = 1 2 1

Ряд является сходящимся.

Следовательно, ряд является расходящимся.

Радикальный признак Коши

Данный признак может быть использован в примерах, которые легко определить. Случай будет характерным тогда, когда член числового ряда – это показательно степенное выражение.

Для того, чтобы закрепить полученную информацию, рассмотрим несколько характерных примеров.

Определить, является ли знакоположительный ряд ∑ k = 1 ∞ 1 ( 2 k + 1 ) k на сходящимся.

Интегральный признак Коши

, то в случае, если несобственный интеграл ∫ a + ∞ f ( x ) d x является сходящимся, то рассматриваемый ряд также сходится. Если же он расходится, то в рассматриваемом примере ряд тоже расходится.

При проверке убывания функции можно использовать материал, рассмотренный на предыдущих уроках.

Рассмотреть пример ∑ k = 2 ∞ 1 k · ln k на сходимость.

Согласно полученным результатам, исходный пример расходится, так как несобственный интеграл является расходящимся.

Признак Раабе

Данный способ определения можно использовать в том случае, если описанные выше техники не дают видимых результатов.

Исследование на абсолютную сходимость

Расходимость знакопеременных рядов

Если ряд ∑ k = 1 ∞ b k – расходящийся, то соответствующий знакопеременный ряд ∑ k = 1 ∞ b k либо расходящийся, либо условно сходящийся.

Признаки для условной сходимости

Признак Лейбница

Ряд условно сходится.

Признак Абеля-Дирихле

∑ k = 1 + ∞ u k · v k сходится в том случае, если < u k >не возрастает, а последовательность ∑ k = 1 + ∞ v k ограничена.

Источник

Степенные ряды в математике с примерами решения и образцами выполнения

Функциональные ряды и их область сходимости:

Пусть — некоторая последовательность функций.

Определение:

называется функциональным рядом.

Если в ряде (1) положить 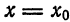то получим числовой ряд

Определение:

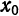
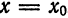
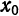
Функциональный ряд (1) называется сходящимся в точке , если числовой ряд (2) полученный из ряда (1) подстановкой , является сходящимся рядом. При этом называется точкой
сходимости ряда.

Пример:

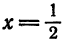
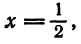
сходится в точке . В самом деле, подставляя в (3) получим числовой ряд

который, как известно, сходится. Данный функциональный ряд расходится в точке 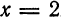, так как числовой ряд

Определение:

Множество всех точек сходимости функционального ряда (1) называется областью сходимости ряда.

Как правило, область сходимости функционального ряда является некоторым промежутком числовой прямой.

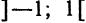
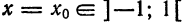
Так, область сходимости функционального ряда (3) совпадает с интервалом . В самом деле, при получаем числовой ряд

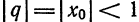
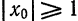
который является рядом геометрической прогрессии со знаменателем и, следовательно, сходится; если же , то ряд (4) расходится.

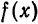
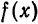
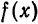
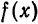
Сумма функционального ряда (1) зависит от взятой точки x области сходимости, следовательно, сумма ряда (1) является некоторой функцией . Область определения суммы ряда совпадает с областью сходимости данного ряда. Говорят также, что ряд (1) сходится к функции и что для функции имеет место разложение

в области сходимости ряда (1).

Например, ряд (3) является рядом геометрической
прогрессии со знаменателем следовательно, для сумма ряда (3) равна функции Таким образом, для имеет место разложение

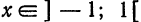
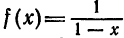
Пример:

Найти область сходимости ряда

Решение:

По признаку Даламбера имеем

Следовательно, ряд сходится на всей числовой прямой.

Пример:

Найти область сходимости ряда

Решение:

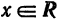
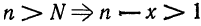
Очевидно, что для любого фиксированного существует такой номер N, что следовательно, общий член ряда не стремится к нулю, т. е. ряд расходится на всей числовой прямой.

Пример:

Исследовать на сходимость ряд

Решение:

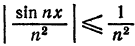
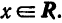
Очевидно, что при любом Так как ряд

сходится, то по признаку сравнения при любом x ряд

также сходится. Следовательно, данный ряд сходится абсолютно на всей числовой прямой.

Пример:

Найти область сходимости ряда

Решение:

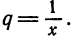
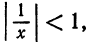
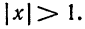
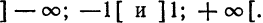
Данный ряд является рядом геометрической прогрессии со знаменателем Следовательно, этот ряд сходится при т. е. при Отсюда получаем, что область сходимости этого ряда состоит из двух интервалов Как и в случае числовых рядов, для
функционального ряда (1) можно составить последовательность
частичных сумм

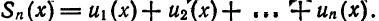
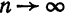
где В каждой точке x из области сходимости ряда (1) его сумма равняется пределу последовательности частичных сумм при :

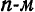
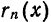
называется остатком ряда (1). Область сходимости ряда (6) совпадает с областью сходимости ряда (1), сумму ряда. (6) тоже называют остатком ряда (1), причем в этом случае

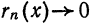
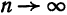
откуда при . Кроме того, из (7) получаем

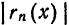
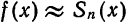
т. е. представляет собой абсолютную погрешность приближения . Как известно, для конечных сумм имеют место следующие свойства: сумма непрерывных функций
является непрерывной функцией; производная суммы равна сумме производных слагаемых; интеграл суммы равен сумме интегралов слагаемых. Для функциональных рядов (бесконечных сумм) эти свойства, вообще говоря, не имеют места. В результате почленного
дифференцирования (интегрирования) функционального ряда можно получить ряд, сумма которого отлична от производной (интеграла) суммы данного ряда или даже расходящийся ряд.

Степенные ряды и их свойства

Определение:

Степенным рядом называется функциональный ряд вида

где x — независимая переменная, постоянные коэффициенты.

Коэффициенты степенного ряда могут быть действительными или комплексными числами. Ограничимся изучением степенных рядов с действительными коэффициентами.

Если произвести замену 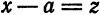, то степенной ряд примет вид

Следовательно, при изучении степенных рядов мы можем ограничиться степенными рядами вида

1. Область сходимости степенного ряда. Переходим теперь к выяснению структуры области сходимости степенного ряда. Заметим вначале, что любой степенной ряд сходится в точке . В самом деле, если подставить в (1) , получим значение Таким
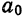
образом, точка входит в области сходимости любого степенного ряда.

Основную роль в определении структуры области сходимости и характера сходимости степенного ряда (1) играет следующая лемма.

Лемма Абеля:

1) Если степенной ряд (1) сходится при некотором значении 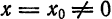, то он абсолютно сходится при любом значении x, для которого

2) Если степенной ряд (1) расходится при некотором значении 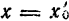то он расходится при любой значении x, для которого

Доказательство:

1) Пусть степенной ряд (1) сходится в точке 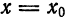следовательно, числовой ряд

является сходящимся. Тогда общий член ряда (2) стремится к нулю при 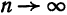. Отсюда следует, что последовательность

ограничена, т. е. существует такое число M, что для всех

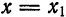
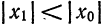
Пусть теперь причем . Мы должны показать, что ряд

сходится. Перепишем ряд (4) в виде

и рассмотрим ряд из модулей членов ряда (5):

В силу неравенства (3) члены ряда (6) меньше соответствующих членов ряда

При ряд (7) является рядом геометрической прогрессии со знаменателем и, следовательно, сходится. Тогда, по признаку сравнения рядов, ряд (6) также сходится, а это означает, что ряд (5) или» что то же самое, (4) сходится абсолютно, что и требовалось доказать.

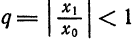
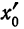
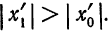
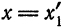
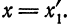
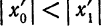
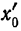
2) Пусть в точке степенной ряд (1) расходится и Мы должны доказать, что при ряд (1) расходится. Допустим противное, что ряд (1) сходится в точке Но тогда, так как , по доказанной первой части данный ряд сходится в точке — получили противоречие. Лемма доказана полностью.

Теорема:

О структуре области сходимости степенного ряда. Если степенной ряд (1) имеет как отличные от нуля точки сходимости, так и точки расходимости, то существует такое число , что ряд (1) абсолютно сходится при всех x из интервала ,
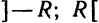
т. е. для которых , и расходится при всех x, для которых .

Доказательство:

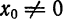
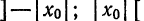
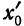
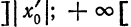
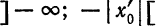
Пусть — точка сходимости ряда (1). Тогда по Лемме Абеля все точки интервала являются точками абсолютной сходимости ряда. Если в точке ряд расходится, то он расходится на полупрямой и на полупрямой (рис. 125). Поэтому интуитивно ясно
(строгое доказательство мы здесь опускаем), что существует такая точка , что при ряд сходится, а при ряд расходится.

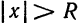
Заметим, что сходимость в точках 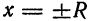зависит от конкретного ряда.

Доказанная теорема позволяет дать полное описание области сходимости ряда (1), поэтому эту теорему называют теоремой о структуре области сходимости степенного ряда.

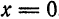
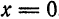
1. Ряд (1) сходится только при . Область сходимости состоит из одной точки .

2. Ряд (1) не имеет точек расходимости. Область сходимости совпадает со всей числовой прямой ;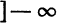

3. Ряд (1) имеет как отличные от нуля точки сходимости, так и точки расходимости. В зависимости от данного ряда, область сходимости является одним из промежутков

Независимо от того, какой именно случай имеет место, интервал 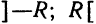называется интервалом сходимости ряда. Следовательно, область сходимости степенного ряда либо совпадает с его интервалом сходимости, либо получается из этого интервала добавлением одной или обеих граничных точек.

Число R называется радиусом сходимости степенного ряда. В случае 1 будем считать , в случае 2 , случаю 3 соответствует значение

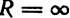
Пример:

Найти область сходимости ряда

Решение:

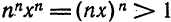
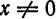
Пусть x — некоторое фиксированное число, отличное от нуля. Тогда существует такой номер N что при n > N выполняется неравенство nx > 1. Следовательно, , т. е. общий член ряда не стремится к нулю. Таким образом, в каждой точке ряд расходится.

Итак, область сходимости данного ряда состоит только из нулевой точки, т. е. R = 0.

Для многих, встречающихся на практике, степенных рядов радиус сходимости можно определить применением признака Даламбера к, ряду

составленному из модулей членов ряда (1). Рассмотрим случай, когда все 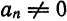; если некоторые коэффициенты равны нулю, например, если x входит только в четных или только в нечетных степенях, то радиус сходимости можно определить, аналогично оперируя с двумя
соседними членами ряда. Для нашего случая имеем:

Пусть предел 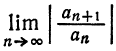существует:

По признаку Даламбера ряд (8) сходится, если

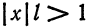
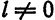
и расходится, если из соотношения (9) при получаем

Таким образом, ряд (8) сходится, а следовательно, ряд (1) сходится абсолютно, если

Отсюда для радиуса сходимости при 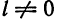получаем соотношение

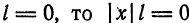
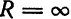
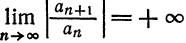
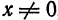
Если ; тогда по признаку Даламбера ряд сходится для любого x, т. е. . В случае ряд расходится для любого , следовательно, .

Из (10) получаем следующую формулу для вычисления радиуса сходимости:

Пример:

Найти область сходимости ряда

Решение:

По формуле (11) имеем

Данный ряд сходится только в точке .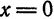

Пример:

Найти область сходимости ряда

Решение:

т. е. R = 2, ряд сходится в интервале 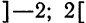. Исследуем ряд на сходимость в концах интервала. При x = 2

получаем числовой ряд

т е. гармонический ряд, который расходится. При 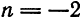приходим к ряду

который по признаку Лейбница сходится.

Итак, областью сходимости будет промежуток .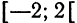

Область сходимости степенного ряда можно определить и применяя непосредственно признак Даламбера. Так, для ряда примера 3 имеем

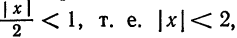
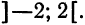
Следовательно, ряд сходится для тех значений x для которых и мы приходим к тому же интервалу После этого надо проверить сходимость на концах интервала.

Пример:

Найти радиус сходимости ряда

Решение:

К этому ряду формула (11)
неприменима, так как отсутствуют нечетные степени переменной 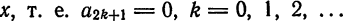Применяем
непосредственно признак Даламбера:

при любом x т. е. ряд сходится на всей числовой прямой.

Пример:

Найти область сходимости ряда

Решение:

Так как 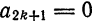, то формула (5) неприменима Применяем признак Даламбера:

Следовательно, ряд сходится для.

Проверим сходимость на концах интервала. При

сходится и 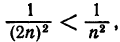то по признаку сравнения сходится и ряд (12)

Таким образом, область сходимости данного ряда совпадает с отрезком .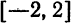

Пример:

Найти область сходимости ряда

Решение:

Применим признак Даламбера:

Следовательно, ряд сходится при

Проверим сходимость на концах полученного интервала.

При 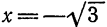получаем ряд

который, очевидно, расходится. При 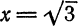получаем ряд

который также расходится._Следовательно, областью сходимости будет .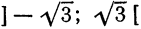

Свойства степенных рядов

В отличие от функционального ряда общего вида, степенные ряды обладают рядом свойств, которые имеют место для обычных многочленов (конечных сумм одночленов вида 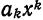). Сформулируем основные свойства степенных рядов.

Свойство:

Сумма степенного ряда (1) является непрерывной функцией в области сходимости ряда.

Свойство:

Если ряд (1) сходится к функции 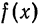, т. e.

то для любого отрезка 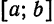содержащегося в области сходимости ряда (1),

Другими словами, степенной ряд можно почленно интегрировать по любому отрезку, содержащемуся в области сходимости.

Заметим, что полученный ряд (14) является числовым рядом. Например, так как ряд

имеет область сходимости 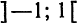, то его можно интегрировать на отрезке

с абсолютной погрешностью

Интегрирование степенных рядов можно использовать для получения разложения в степенной ряд функций вида 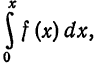если известно разложение (13)

функции в степенной ряд. Для этого достаточно степенной ряд (13) интегрировать на отрезке для любого x из области сходимости ряда (13) (тогда, как известно, и весь отрезок принадлежит области сходимости):

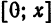
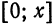
Полученный ряд (16), в отличие от ряда (14), является функциональным, даже степенным рядом (так как все интегралы, входящие в (16), имеют переменный верхний предел), и имеет тот же интервал сходимости, что и ряд (13).

Таким образом, из свойства 2 получаем: если для функции в некотором интервале имеет место разложение (13), то для функции имеет место о разложение (16) в том же интервале.

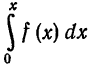
Пример:

Заменяя в (15) x на—x, получаем ряд

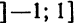
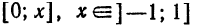
областью сходимости которого является промежуток . Интегрируя ряд (17) на отрезке , получаем

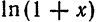
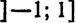
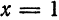
Полученный ряд (18) представляет собой разложение функции в степенной ряд в промежутке . Отсюда, например, при получаем

Пример:

Заменяя в (17) x на 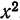получим разложение

в промежутке 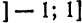. Интегрируя ряд (19) на отрезке

Подставляя в (20) х = 1 и учитывая, что 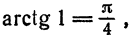получим ряд

который может быть использован для приближенного вычисления числа .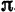

Свойство:

Если ряд (1) сходится к функции 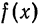т. е. имеет место равенство (7), то ряд

составленный из производных членов ряда (1), имеет тот же радиус сходимости и сходится к производной функции т. е.

Другими словами, степенной ряд можно почленно дифференцировать в любой внутренней точке из области его сходимости.

Пример:

Дифференцируя почленно равенство (17), получим

Замечание:

Если степенной ряд имеет вид

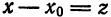
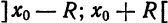
то подстановкой он приводится к степенному ряду вида (1). Интервалом сходимости степенного ряда (22) будет .

Пример:

Найти область сходимости степенного ряда

Решение:

Следовательно, ряд сходится при 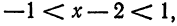т. е.
при

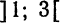
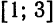
Проверкой убеждаемся, что данный ряд сходится на концах интервала . Следовательно, областью сходимости является отрезок .

Формула Тейлора и ее остаточный член

Пусть функция определена в точке и имеет в некоторой окрестности этой точки все производные до (n + 1)-го порядка включительно. Тогда для функции можно составить выражение

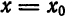
которое называется многочленом Тейлора степени n для функции в точке . Из (1) видно, что при

. Подсчеты показывают, что для многих функций, встречающихся в математике, физике, технике и других областях, многочлены Тейлора для значений x, близких к , принимают значения, близкие к . Обозначив абсолютную погрешность, т. е. разность , через , получим
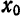
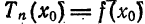
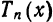
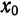
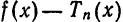
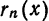
формулу 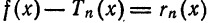, или

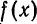
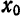
Формула (2) называется формулой Тейлора для функции в точке .

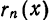
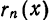
Функция называется остаточным членом формулы Тейлора, Известны различные выражения для остаточного члена .

Следующая формула выражает остаточный член в форме Лагранжа:

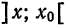
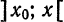
где t — некоторая точка интервала при и интервала при .

Учитывая (3), формулу Тейлора (2) можно писать в виде

Если 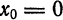, то формула Тейлора (4) принимает вид

где , причем t и x одного знака.

Формула (5) известна под названием формулы Маклорена.

Пример:

Найти формулу Маклорена для функции 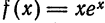с остаточным членом в форме Лагранжа для n = 4.

Решение:

Находим производные до порядка 4 + 1 = 5 включительно:

При n = 4 из (5) имеем:

аналогично, Следовательно,

где и x — одного знака.

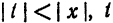
Ряд Тейлора

Дана функция , которая имеет производные любого порядка в точке . Тогда можно составить ряд

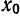
Ряд (1) называется рядом Тейлора для функции в точке . Функция называется порождающей для ряда Тейлора (1).

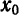
Сходимость ряда Тейлора к порождающей функции. Вообще говоря, составленный ряд (1) для функции может быть расходящимся, может сходиться в некотором промежутке, но его сумма необязательно должна равняться порождающей функции . Поэтому очень важно знать условия, при которых ряд (1) сходится к порождающей его функции . Приводим необходимое и достаточное условие сходимости ряда Тейлора к порождающей его функции.

Теорема:

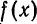
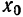
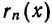
Ряд Тейлора (1) сходится к порождающей функции в некоторой окрестности точки тогда и только тогда, когда остаточный член в формуле Тейлора для функции в каждой точке этой окрестности стремится к нулю.

Доказательство:

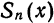
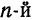
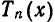
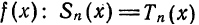
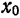
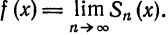
Легко видеть, что n-я частичная сумма ряда (1) совпадает с многочленом Тейлора степени для функции Пусть теперь ряд (1) сходится к функции в некоторой окрестности точки т. е. Тогда

Обратно, пусть 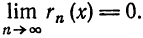Тогда

Следующая теорема дает только достаточное условие сходимости ряда Тейлора к порождающей функции и может быть применена при разложении функций.

Теорема:

Если все производные функции ограничены в некоторой окрестности точки то для любого x из этой окрестности ряд Тейлора функции сходится к функции , т. е. имеет место
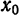
разложение

Доказательство:

В силу теоремы 1 достаточно показать, что 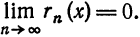Из условия нашей теоремы следует существование такого числа M, что для любого n

для любого x из рассматриваемой окрестности. Беря остаточный член в форме Лагранжа (формула (3) предыдущего параграфа), имеем:

Осталось показать, что 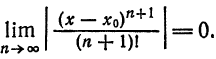Для этого заметим, что ряд

сходится при любом x: (это можно проверить по признаку Даламбера; см. пример 2 § 1). Следовательно, его общий член стремится к нулю,
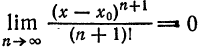
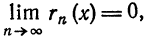
т. е. Отсюда получаем и тогда из теоремы 1 следует требуемое равенство (2).

Единственность разложения функции в степенной ряд

Теорему об единственности разложений функций в степенных рядах можно сформулировать следующим образом.

Теорема:

Если функция разлагается в некотором промежутке в степенной ряд

то это разложение единственно и совпадает с рядом Тейлора функции в точке , т. е.

Доказательство:

Почленным дифференцированием из (4) получаем:

Подставляя 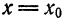в формулу (4) и в полученные формулы для производных функции , получим:

Из этих соотношений найдем, что

Следовательно, ряд (4) совпадает с рядом Тейлора (1) функции в точке . Теорема доказана.

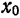
Если в (1) взять 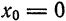то получаем ряд

который является частным случаем ряда Тейлора и известен под названием ряда Маклорена для функции . Из формулу (2) при получаем разложение функции в ряд Маклорена:

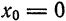
Ряды Тейлора для некоторых элементарных функций

Рассмотрим разложение в ряд Тейлора некоторых элементарных функций. При этом ограничимся частным случаем 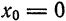, т. е. рядами Маклорена, которые чаще используются на практике.

Для разложения некоторой функции в ряд Маклорена надо вычислить значения всех производных данной функции при и воспользоваться формулой (5) предыдущего параграфа.

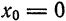
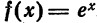
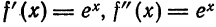
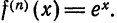
1. Разложение функции . Заметим, что и, вообще, Отсюда

Таким образом, функции 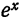сопоставляется ряд

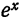
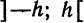
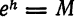
Покажем, что равна сумме этого ряда. Для данного x найдем интервал , содержащий число x и обозначим . Тогда для любой производной функции имеем

Отсюда по теореме 3 § 4 сумма ряда равна порождающей его функции, т. е.

Разложение функции

Найдем производные данной функции:

Вычислим значения функции и ее производных для

Вообще, если n четное, т. е. 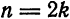где

если n нечетное, то рассмотрим случаи:

Для первого случая имеем:

Для второго случая имеем:

Учитывая далее, что производные функции sin x ограничены на всей числовой прямой,

по теореме 3 § А получаем

Отбросив члены с нулевыми коэффициентами, получим

Разложение функции

Повторяя рас суждения и выкладки, аналогичные случаю функции , получим . Отсюда при нечетном n, т. е. при , получим для четного n рассмотрим отдельно случаи при имеем при имеем

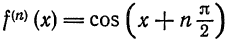
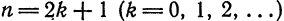
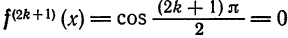
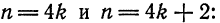
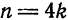
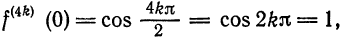
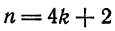
Заметим, что согласно теореме 2 § 4 функции 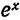, sin x; и cos x; разлагаются в свои ряды Маклорена на всей числовой оси.

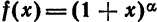
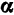
Разложение функции , где — произвольное действительное число

следовательно, функции 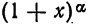сопоставляется следующий ряд Маклорена:

По признаку Даламбера найдем область сходимости полученного ряда (4):

Следовательно, ряд сходится при , т. е. в интервале , и расходится при .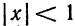

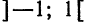
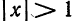
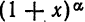
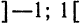
Примем без доказательства, что ряд (4) сходится к порождающей функции в интервале сходимости .Таким образом,

для

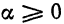
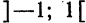
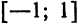
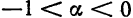
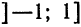
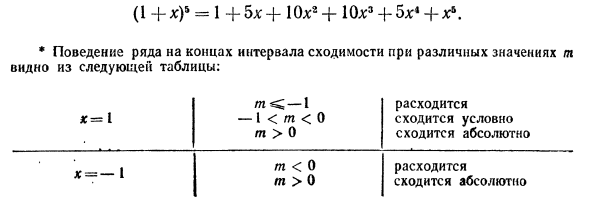
Более того, можно показать, что при разложение (5) верно и в обоих концах интервала , т. е. имеет место на отрезке , а при — в правом конце, т. е. на полуинтервале .

Ряд (5) называется биномиальным рядом.

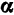
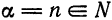
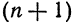
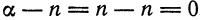
Если — натуральное число, , то все члены формулы (5), начиная с — го, равны нулю, так как содержат множитель . В этом случае биномиальный ряд (5) представляет собой известную формулу бинома Ньютона:

Указанный в этом параграфе метод разложения функций в степенной ряд может быть применен к произвольной функции. Однако в отдельных случаях вычисления и обоснование сходимости могут оказаться очень громоздкими. Разложения некоторых функций в ряд можно получить, выполняя те или иные преобразования

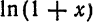
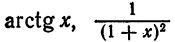
над имеющимися разложениями. Так, в примерах 7, 8, 9 § 2 получены разложения для функций , при помощи замены переменной, интегрирования и дифференцирования степенных рядов. Заметим, например, что разложение (3) функции cos x можно получить путем почленного дифференцирования
из разложения (2) функции sin x.

Элементарные функции в области комплексных чисел

Как мы отметили, можно рассматривать степенные ряды не только с действительными, но и с комплексными значениями коэффициентов и переменной x.

Степенные ряды представляют собой удобное средство для определения функций от комплексного переменного Так, имея разложение показательной функции

на действительной оси, распространяем эту формулу на комплексной плоскости, т. е. для показательной функции 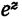от комплексного переменного z принимается следующее определение:

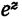
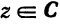
Показательной функцией от комплексной переменной называется функция, заданная формулой

Аналогично, тригонометрические функции sin z и cos z для комплексного переменного 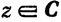определяются по формулам:

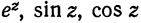
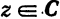
Можно показать, что по формулам (7), (8) и (9) функции определены для всех , т. е. что соответствующие ряды сходятся на всей комплексной плоскости.

Используя определения (7), (8), (9) функций 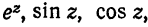можно вывести формулу Эйлера (см. § 8

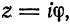
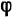
гл. 9). Полагая в формуле (7) где — действительное число, получим

Отделяя действительные и мнимые части, находим

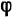
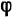
Так как в правой части (10) в скобках стоят соответственно разложения в ряды cos и sin , то получаем формулу Эйлера

Примеры практического применения степенных рядов

Вычисление значений функций

Пример:

Вычислить число e, т. е. значение функции 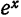при x = 1, с точностью до 0,001 (если известно, что e

причем абсолютная погрешность этого приближения равна

где 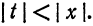При x = 1 получаем

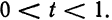
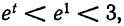
где Но так как то

Число n определим из неравенства

Достаточно взять n = 6, так как

Пример:

Вычислить sin 18° с четырьмя верными десятичными знаками.

Решение:

По формуле (2) § 5 имеем

Так как угол 18° в радианной мере (с точностью до 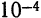) равен 0,3142, то

Так как мы имеем знакочередующийся ряд, то при замене его суммы некоторой частичной суммой абсолютная погрешность не превышает модуля первого отброшенного члена. Непосредственной проверкой убеждаемся, что 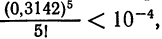следовательно, достаточно
ограничиться двумя членами:

Вычисление определенных интегралов

Пример:

с точностью до. 0,0001.

Решение:

Из формулы (2) § 5 делением обеих частей на x находим

Это разложение, как и разложение для sin x, имеет место на всей числовой оси, поэтому его можно почленно интегрировать:

При x = 1 имеем

Полученный ряд является знакочередующимся рядом. Так как

то достаточно взять

Вычисляя промежуточные результаты с пятью десятичными знаками, получим окончательный результат с четырьмя верными десятичными знаками:

Пример:

Вычислить интеграл 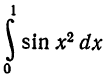с точностью до 0,0001.

Решение:

Заменяя в разложении 2 § 5 x на 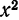, получаем

При x = 1 поручаем знакочередующийся ряд:

имеет границу абсолютной погрешности

Таким образом, вычисляя промежуточные результаты с пятью десятичными знаками, получим окончательный результат с четырьмя верными десятичными знаками:

Замечание. Интегралы, рассмотренные в примерах 3 и 4, как мы знаем, не берутся в элементарных функциях. Однако изложенный метод вычисления интегралов оказывается удобным и в тех случаях, когда интегралы выражаются; через элементарные функции.

Пример:

Вычислить интеграл

Однако практическое применение этого результата приводит к громоздким вычислениям. Намного проще вычисляется данный интеграл при помощи степенных рядов.

Решение:

Заменяя в известном разложении

x на 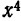получаем

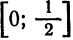
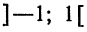
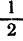
Так как отрезок содержится в интервале сходимости полученного ряда, то этот ряд можно почленно интегрировать в пределах от 0 до :

Учитывая, что полученный ряд знакочередующийся, получаем, что приближение

имеет границу абсолютной погрешности

В действительности, все цифры верные.

Решение дифференциальных уравнений

Пусть дано некоторое дифференциальное уравнение

Требуется найти его решение, удовлетворяющее
начальным условиям:

Изложим схему получения искомого решения в виде ряда Тейлора.

Подставляя значения (2) в уравнение (1), получим уравнение

из которого можно определить значение n-й производной

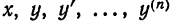
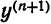
Дифференцируя равенство (1), получим уравнение, которое помимо будет содержать и производную :

Подставляя в (4) значения (2) и (3), получим уравнение

из которого можно определить значение (n+1)-й производной. Продолжая так и далее, находим последовательно значения всех производных искомой функции y в точке x = 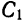. По этим данным можно написать разложение искомого решения у в ряд Тейлора в точке Таким образом, решение уравнения (1) получается в виде степенного ряда.

Пример:

Найти решение дифференциального уравнения

удовлетворяющее начальным условиям

Решение:

Дифференцируя (5), получаем

Дифференцируя (6), находим

Дифференцируя (7), находим

и т. д. Поскольку 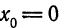, получаем разложение решения в ряд Маклорена:

Пример:

Найти частное решение дифференциального уравнения

удовлетворяющее начальным условиям

Решение:

Из (8) имеем: 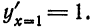Дифференцируя (8), находим

Из (9) имеем 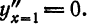Дифференцируем (9):

отсюда 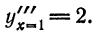Дифференцируем (10):

отсюда 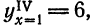и т. д. Следовательно, искомое решение записывается в виде ряда Тейлора в точке :

Дополнение к степенным рядам

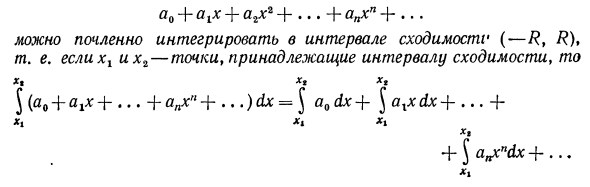
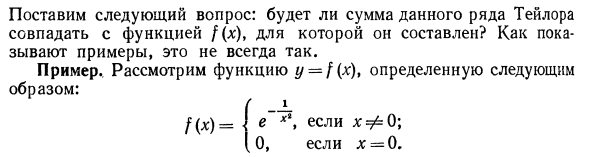
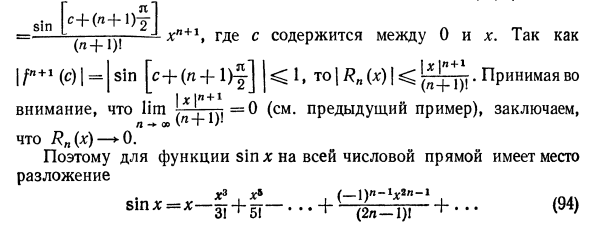
Решение степенных рядов

Теорема Абеля. Интервал и радиус сходимости степенного ряда

Степенным рядом называется функциональный ряд вида

где коэффициенты — постоянные.

Ряд (2) формальной заменой сводится к ряду (1). Степенной ряд (1) всегда сходится в точке х = 0, а ряд (2) — в точке Х0, и их сумма в этих точках равна

Пример:

являются степенными рядами.

Выясним вид области сходимости степенного ряда.

Теорема:

Абель. Если степенной ряд

сходится при то он сходится абсолютно для всех х таких, что если степенной ряд расходится при х = x2, то он расходится при любом х, для которого

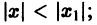
Пусть степенной ряд

сходится при 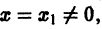т. е. сходится числовой ряд

Отсюда следует, что

а значит, существует число М > 0 такое, что 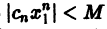для всех n. Рассмотрим ряд

где 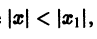и оценим его общий член. Имеем

где 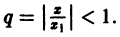Но ряд

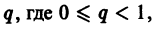
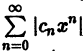
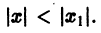
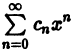
составлен из членов геометрической прогрессии со знаменателем и значит, сходится. На основании признака сравнения ряд сходится в любой точке х, для которой Следовательно, степенной ряд абсолютно сходится для

Пусть теперь степенной ряд

расходится при х = х2. Допустим, что этот ряд сходится для |х| > |х2|. По доказанному он должен сходиться и при х = х2, так как |х2|

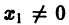
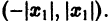
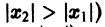
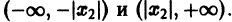
Пусть в точке ряд сходится. Тогда ряд будет абсолютно сходиться в интервале Если в некоторой точке х2 (здесь ряд расходится, то он будет расходиться и в бесконечных интервалах В этих условиях на оси Ох существуют две точки (симметричные относительно начальной точки О), которые отделяют интервалы расходимости от интервала сходимости. Имеет место следующая теорема.

Теорема:

Пусть степенной ряд

сходится в точке 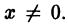Тогда либо этот ряд абсолютно сходится в каждой точке числовой прямой, либо существует число R > 0 такое, что ряд сходится абсолютно при |х| R.

Определение:

Интервалом сходимости степенного ряда

называется интервал (-R, R), где R > 0, такой, что в каждой точке 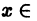(-R, R) ряд абсолютно сходится, а в точках х таких, что |х| > R, ряд расходится. Число R называется радиусом сходимости степенного ряда.

Замечание:

Замечание:

где 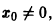имеет тот же радиус сходимости, что и ряд

но его интервалом сходимости является интервал

При условии существования конечного предела

радиус сходимости степенного ряда 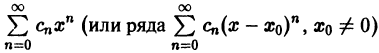можно найти по формуле

Для доказательства формулы (3) рассмотрим ряд, составленный из абсолютных величин членов данного ряда

Применяя к этому ряду признак Даламбера, находим

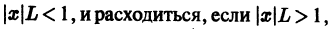
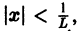
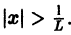
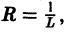
Отсюда следует, что ряд (4) будет сходиться, если т. е. степенной ряд сходится абсолютно для всех х таких, что и расходится при По определению радиуса сходимости получаем, что т. е.

Радиус сходимости степенного ряда можно находить также по формуле

если существует конечный предел

Формулу (5) легко получить, используя признак Коши. Если степенной ряд

сходится только в точке х = 0, то говорят, что его радиус сходимости R = 0 (это возможно, например, при

Если степенной ряд сходится во всех точках числовой оси, то полагают 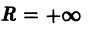(это имеет место, например, при

Областью сходимости степенного ряда

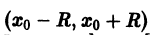
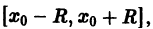
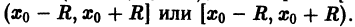
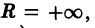
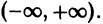
может оказаться либо интервал , либо отрезок либо один из полуинтервалов Если то областью сходимости ряда будет вся числовая ось, т. е. интервал Для отыскания области сходимости степенного ряда

нужно сначала вычислить его радиус сходимости R (например, по одной из приведенных выше формул) и тем самым найти интервал сходимости 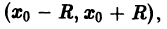в котором рад абсолютно сходится, затем — исследовать «сходимость рада в концах интервала сходимости — в точках

Пример:

Найти область сходимости степенного ряда

1) Для нахождения радиуса сходимости R данного ряда удобно применить формулу (3). Так как 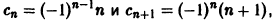то будем иметь

Ряд сходится абсолютно на интервале — 1

расходимость которого очевидна (не выполнен необходимый признак сходимости: 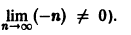При х = 1 получим числовой ряд

не существует, а значит, этот ряд расходится.

1) Радиус сходимости находим по формуле (3). Имеем

Ряд (7) сходится абсолютно на интервале

который расходится (гармонический ряд). При х = 0 будем иметь числовой ряд

Таким образом, ряд (7) сходится в области

Пример:

Найти интервал сходимости ряда

Так как 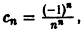то для нахождения радиуса сходимости применим формулу (5):

Это означает, что данный ряд сходится при всех значениях х, т.е. областью сходимости является интервал

Пример:

Найти интервал сходимости ряда

то получим

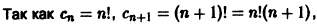
Равенство R = 0 означает, что ряд (8) сходится только в точке x = 0, т. е. область сходимости данного степенного ряда состоит из одной точки х = 0.

Равномерная сходимость степенного ряда и непрерывность его суммы

Теорема:

сходится абсолютно и равномерно на любом отрезке [-а, а], а > 0, содержащемся в интервале сходимости ряда (-R, R), R > 0.

Пусть 0

непрерывна в каждой точке х его интервала сходимости (-R, R), R > 0.

Любую точку х из интервала сходимости (-R, R) можно заключить в некоторый отрезок [-а, а], 0 Интегрирование степенных рядов

Теорема:

О почленном интегрировании степенного ряда. Степенной ряд

можно интегрировать почленно в его интервале сходимости (-R, R), R > 0, причем радиус сходимости ряда, полученного почленным интегрированием, также равен R. В частности, для любого х из интервала (-R, R) справедлива формула

Любую точку х из интервала сходимости (-R, R) можно заключить в некоторый отрезок [-а, а], где 0

Найдем радиус сходимости R’ полученного ряда

при дополнительном условии существования конечного предела 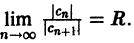Имеем

Итак, радиус сходимости степенного ряда при интегрировании не меняется.

Замечание:

Утверждение теоремы остается справедливым и при

Дифференцирование степенных рядов

Теорема:

О почленном дифференцировании степенного ряда. Степенной ряд

можно дифференцировать почленно в любой точке х его интервала сходимости (-R, R), R > 0, при этом выполняется равенство

Пусть R — радиус сходимости ряда

a 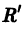— радиус сходимости ряда

Предположим, что существует (конечный или бесконечный) предел

Найдем радиус R’ ряда

Тем самым, радиусы сходимости рядов (1) и (2) равны. Обозначим сумму ряда (2) через

Ряды (1) и (2) равномерно сходятся на любом отрезке [-а, а], где 0

можно почленно дифференцировать сколько угодно раз в любой точке х его интервала сходимости (-R, R), причем радиусы сходимости всех получаемых рядов будут равны R.

Ряд Тейлора

Определение:

Будем говорить, что функция f(х) разлагается в степенной ряд 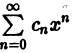на интервале (-R, R), если на этом интервале указанный ряд сходится и его сумма равна f(х):

Докажем сначала, что функция f(x) не может иметь двух различных разложений в степенной ряд вида (1).

Теорема:

Если функция f(х) на интервале (-R, R) разлагается в степенной ряд (1), то это разложение единственно, т. е. коэффициенты ряда (1) по его сумме определяются однозначно.

Пусть функция f(х) в интервале (-R, R) разложена в сходящийся степенной ряд

Дифференцируя этот ряд почленно n раз, найдем

(здесь

Таким образом, коэффициенты 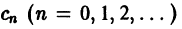степенного ряда (1) формулой (2) определяются однозначно.

Замечание:

Если функция f(x) разложена в степенной ряд по степеням разности

то коэффициенты сn этого ряда определяются формулами

вычислив его коэффициенты по формуле (3).

Определение:

Рядом Тейлора функции f(х) относительно точки х0 называется степенной ряд вида

Коэффициенты этого ряда

называются коэффициентами Тейлора функции f(х). При X0 = 0 ряд Тейлора

называют рядом Маклорена.

Из теоремы 5 вытекает следующее утверждение.

Теорема:

Если на интервале 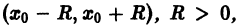функция f(х) разлагается в степенной ряд

то этот ряд является рядом Тейлора функции f(х).

Пример:

и найдем ее производные.

Для 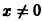эта функция имеет производные всех порядков, которые находятся по обычным правилам

где 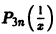— многочлен степени Зn относительно

Покажем теперь, что в точке х = 0 данная функция также имеет производные любого порядка, причем все они равны нулю. Исходя из определения производной, имеем

(при вычислении предела мы применили правило Лопиталя). Аналогичным образом можно доказать, что

Тем самым, заданная функция имеет на числовой оси производные всех порядков,

Построим формальный ряд Тейлора исходной функции относительно точки Xо = 0. Имеем

Очевидно, что сумма S(x) этого ряда тождественно равна нулю, в то время как сама функция f(x) тождественно равной нулю не является.

Про этот пример стоит вспомнить при обсуждении комплексного анализа (аналитичности): функция, внешне совершенно благопристойная, проявляет на действительной оси капризный характер, являющийся следствием неприятностей на мнимой оси.

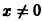
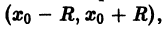
Формально построенный в примере для заданной бесконечно дифференцируемой функции ряд сходится, но его сумма не совпадает со значениями этой функции при . В связи с этим возникает естественный вопрос: каким условиям должна удовлетворять функция f(х) на интервале чтобы ее можно было разложить в сходящийся к ней ряд Тейлора?

Условия разложимости функции в ряд Тейлора

Для простоты будем рассматривать степенной ряд вида

Теорема:

Для того чтобы функцию f(x) можно было разложить в степенной ряд

на интервале (-R, R), необходимо и достаточно, чтобы на этом интервале функция f(х) имела производные всех порядков и чтобы в ее формуле Тейлора

остаточный член Rn(x) стремился к нулю при 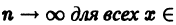(-R, R).

Необходимость:

Пусть на интервале (-R,R), R > 0, функция f(х) разложима в степенной ряд

т. е. ряд (2) сходится и его сумма равна f(х). Тогда по теореме 4 и следствию из нее функция f(х) имеет на интервале (-R, R) производные 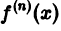всех порядков. По теореме 5 (формула (2)) коэффициенты ряда (2) имеют вид

т. е. мы можем написать равенство

В силу сходимости этого ряда на интервале (-R, R) его остаток

стремится к нулю при 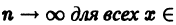(-R, R).

Достаточность:

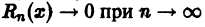
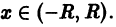
Пусть функция f(х) на интервале (-R, R) имеет производные всех порядков и в ее формуле Тейлора остаточный член для любого Поскольку

при 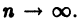Поскольку в квадратных скобках записана n-я частичная сумма ряда Тейлора, то формула (4) означает, что ряд Тейлора функции f(х) сходится на интервале (-R, R) и его суммой является функция f(х).

Достаточные условия разложимости функции в степенной ряд, удобные для практического применения, описываются следующей теоремой.

Теорема:

Для того, чтобы функцию f(х) на интервале (-R, R) можно разложить в степенной ряд

достаточно, чтобы функция f(х) имела на этом интервале производные всех порядков и чтобы существовала постоянная М > 0 такая, что

для всех n = 0, 1, 2,… и для всех

Пусть функция f(х) имеет на интервале (-R, R) производные всех порядков. Тогда для нее можно формально написать ряд Тейлора

Докажем, что он сходится к функции f(х). Для этого достаточно показать, что остаточный член

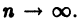
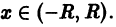
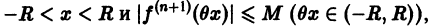
в формуле Тейлора (1) стремится к нулю при для всех В самом деле, учитывая, что будем иметь

для n = 0, 1,… и для всех 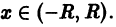Числовой ряд

сходится в силу признака Даламбера:

в силу необходимого признака сходимости. Из неравенства (3) получаем

для всех

Продолжение примера 1. Хотя функция из примера 1 и имеет на числовой оси производные всех порядков, универсальной постоянной М, ограничивающей их абсолютные величины, не существует,

при

Ряды Тейлора элементарных функций

Рассмотрим разложения в ряд

основных элементарных функций.

Эта функция имеет производные всех порядков на интервале (-а, а), где а > 0 — любое число, причем

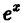
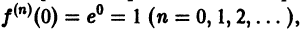
Следовательно, показательная функция разлагается в ряд Тейлора на любом интервале (-а, а) и, тем самым, на всей оси Ох. Так как то получаем ряд

Радиус сходимости этого ряда

Если в разложении (1) заменить х на —х, то будем иметь

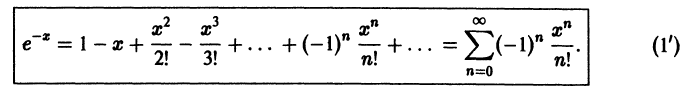
Данная функция имеет производные любого порядка, причем

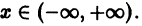
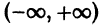
для n = 0, 1, 2,… и Тем самым, по теореме 8 функция sin а: разлагается в сходящийся к ней на интервале ряд Тейлора. Так как

то этот ряд имеет следующий вид

Радиус сходимости ряда

Аналогично получаем, что

любое действительное число.

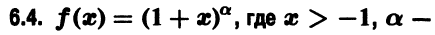
Эта функция удовлетворяет соотношению

Будем искать степенной ряд, сумма которого S(х) удовлетворяет соотношению (4) и условию S(0) = 1. Положим

Подставляя соотношения (5) и (6) в формулу (4), будем иметь

Приравнивая коэффициенты при одинаковых степенях х в левой и правой частях равенства, получим

Подставляя эти значения коэффициентов в соотношение (5), получим ряд

Найдем радиус сходимости ряда (7) в случае, когда а не является натуральным числом. Имеем

Итак, ряд (7) сходится при |х|

Так как S(х) удовлетворяет соотношению (4), т. е.

то для производной функции 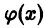получаем:

для 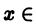(-1,1). Отсюда следует, что

на (-1, 1). В частности, при х = 0 имеем

и значит,

Для получения разложения этой функции в ряд Тейлора по степеням х проинтегрируем равенство (9) в пределах от 0 до х, где 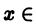(-1,1). Имеем

Пользуясь этой таблицей, можно получать разложения в степенной ряд более сложных функций. Покажем на примерах, как это делается.

Пример:

в степенной ряд в окрестности точки Хо = 2, т.е. по степеням разности х — 2.

Преобразуем данную функцию так, чтобы можно было использовать ряд (10) для функции 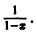Имеем

Заменяя в формуле (10) х на 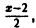получим

Это разложение справедливо, когда выполнено любое из эквивалентных неравенств

Пример:

Разложить по степеням х функцию

используя формулу (10).

Разлагая знаменатель на множители, представим данную рациональную функцию в виде разности двух простейших дробей. Имеем

После простых преобразований получим

К каждому слагаемому в правой части равенства (13) применяем формулу (10), в результате чего получим степенные ряды

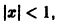
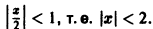
Ряд (14) сходится для а ряд (15) сходится для Оба ряда (14) и (15) будут сходиться одновременно для |x|

радиус сходимости которого равен R = 1.

Этот ряд сходится абсолютно для |x|

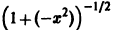
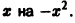
Применим к функции формулу (8), заменяя в ней В результате для |-X2| = получаем

Интегрируя обе части последнего равенства от нуля до x (почленное интегирование законно, так как степенной ряд равномерно сходится на любом отрезке с концами в точках 0 и x, лежащем в интервале (-1,1)), найдем

Тем самым, окончательно получаем, что

Известно, что первообразная для функции 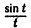не выражается через элементарные функции. Разложим подынтегральную функцию в степенной ряд, пользуясь тем, что

Из равенства (16) находим

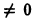
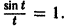
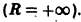
Заметим, что деление ряда (16) на t при t законно. Равенство (17) сохраняется и при t = 0, если считать, что при t = 0 отношение Тем самым, ряд (17) сходится при всех значениях t Интегрируя его почленно, получим

Полученный ряд — знакочередующийся, так что погрешность при замене его суммы частичной суммой оценивается просто.

Пример:

Здесь первообразная для подынтегральной функции 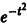также не является элементарной функцией. Для вычисления интеграла заменим в формуле

х на 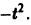Получим

Проинтегрируем обе части этого равенства в пределах от 0 до х:

Этот ряд сходится при любых х (его радиус сходимости 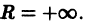и является знакочередующимся при х > 0.

Степенные ряды основные определения и свойства с подробным объяснением и теорией

Функциональные ряды

Ряд, членами которого являются функции от х, называется функциональным:

Придавая x определенное значение , мы получим числовой ряд

который может быть как сходящимся, так и расходящимся.

Если полученный числовой ряд сходится, то точка называется точкой сходимости ряда (62.1); если же ряд расходится — точкой расходимости функционального ряда.

Совокупность числовых значений аргумента х, при которых функциональный ряд сходится, называется его областью сходимости.

В области сходимости функционального ряда его сумма является некоторой функцией от х: S = S(x). Определяется она в области сходимости равенством

частичная сумма ряда.

Пример:

Найти область сходимости ряда

Решение:

Данный ряд является рядом геометрической прогрессии со знаменателем q = х. Следовательно, этот ряд сходится при |х|

Пример:

Исследовать сходимость функционального ряда

Решение:

Составим ряд из абсолютных величин членов исходного ряда:

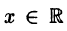
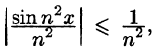
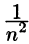
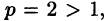
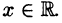
Так как при любом имеет место соотношение а ряд с общим членом сходится (обобщенный гармонический ряд, см. п. 60.4), то по признаку сравнения ряд (62.2) сходится при Следовательно, исходный ряд абсолютно сходится при всех

Среди функциональных рядов в математике и ее приложениях особую роль играет ряд, членами которого являются степенные функции аргумента х, т. е. так называемый степенной ряд

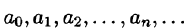
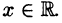
Действительные (или комплексные) числа называются коэффициентами ряда (62.3), — действительная переменная.

Ряд (62.3) расположен по степеням х. Рассматривают также степенной ряд, расположенный по степеням 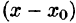, т. е. ряд вида

где — некоторое постоянное число.

Ряд (62.4) легко приводится к виду (62.3), если положить 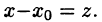Поэтому при изучении степенных рядов можем ограничиться степенными рядами вида (62.3).

Сходимость степенных рядов

Выясним вопрос о сходимости степенного ряда (62.3). Область сходимости степенного ряда (62.3) содержит по крайней мере одну точку: х = 0 (ряд (62.4) сходится в точке ).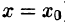

Теорема Н.Абеля

Об области сходимости степенного ряда можно судить, исходя из следующей теоремы.

Теорема:

Абель. Если степенной ряд (62.3) сходится при 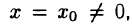то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству

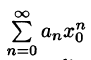
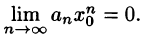
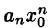
По условию ряд сходится. Следовательно, по необходимому признаку сходимости Отсюда следует, что величинаограничена, т. е. найдется такое число М > 0, что для всех п выполняется неравенство

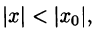
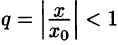
Пусть тогда величина и, следовательно,

т. е. модуль каждого члена ряда (62.3) не превосходит соответствующего члена сходящегося (q Интервал и радиус сходимости степенного ряда

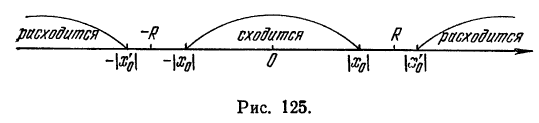
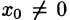
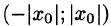
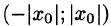
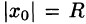
Из теоремы Абеля следует, что если есть точка сходимости степенного ряда, то интервал весь состоит из точек сходимости данного ряда; при всех значениях х вне этого интервала ряд (62.3) расходится.

Интервал и называют интервалом сходимости степенного ряда. Положив , интервал сходимости можно записать в виде (—R;R). Число R называют радиусом сходимости степенного ряда, т. е. R > 0 — это такое число, что при всех х, для которых |х| R ряд расходится (см. рис. 259).

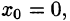
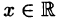
В частности, когда ряд (62.3) сходится лишь в одной точке то считаем, что R = 0. Если же ряд (62.3) сходится при всех значениях (т. е. во всех точках числовой оси), то считаем, что

Отметим, что на концах интервала сходимости (т. е. при х = R и при х = —R) сходимость ряда проверяется в каждом случае отдельно.

Для нахождения радиуса сходимости степенного ряда (62.3) можно поступить следующим образом. Составим ряд из модулей членов данного степенного ряда

и применим к нему признак Даламбера. Допустим, что существует предел

По признаку Даламбера ряд сходится, если 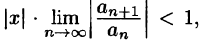т. е. ряд сходится при тех значениях х, для которых

ряд, составленный из модулей членов ряда (62.3), расходится при тех значениях х, для которых 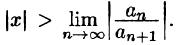Таким образом, для ряда (62.3) радиус абсолютной сходимости

Аналогично, воспользовавшись радикальным признаком Коши, можно установить, что

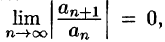
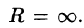
Замечания. 1. Если то можно убедиться, что ряд (62.3) абсолютно сходится на всей числовой оси. В этом случае Если

2.Интервал сходимости степенного ряда (62.4) находят из неравенства 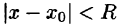, имеет вид

3.Если степенной ряд содержит не все степени х, т. е. задан неполный степенной ряд, то интервал сходимости ряда находят без определения радиуса сходимости (формулы (63.1) и (63.2)), а непосредственно применяя признак Даламбера (или Коши) для ряда, составленного из модулей членов данного ряда.

Пример:

Найти область сходимости ряда

Решение:

Воспользуемся формулой (63.1):

Следовательно, данный ряд абсолютно сходится на всей числовой оси.

Пример:

Найти область сходимости ряда

Решение:

Заданный ряд неполный. Воспользуемся признаком Даламбера. Для данного ряда имеем:

Ряд абсолютно сходится, если 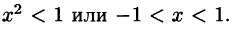Исследуем поведение ряда на концах интервала сходимости.

При х = — 1 имеем ряд 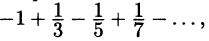который сходится по

При х = 1 имеем ряд 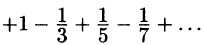это тоже сходящийся лейбницевский ряд. Следовательно, областью сходимости исходного ряда является отрезок [-1; 1].

Пример:

Найти область сходимости ряда

Решение:

Находим радиус сходимости ряда по формуле (63.1):

Следовательно, ряд сходится при — 2

который сходится по признаку Лейбница. При х = 0 имеем расходящийся ряд

Следовательно, областью сходимости исходного ряда является полуотрезок [-4; 0).

Свойства степенных рядов

Сформулируем без доказательства основные свойства степенных рядов.

1. Сумма S(x) степенного ряда (62.3) является непрерывной функцией в интервале сходимости (—R; R).

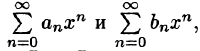
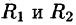
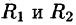
2.Степенные ряды имеющие радиусы сходимости соответственно , можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядов не меньше, чем меньшее из чисел .

3.Степенной ряд внутри интервала сходимости можно почленно дифференцировать; при этом для ряда

при —R

4. Степенной ряд можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости; при этом для ряда (63.3) при — R

Ряды (63.4) и (63.5) имеют тот же радиус сходимости, что и исходный степенной ряд.

Перечисленные свойства 1-4 остаются справедливыми и для степенных рядов вида (62.4).

Свойства степенных рядов широко используются в теоретических исследованиях и в приближенных вычислениях.

Разложение функции в степенные ряды

Ряды Тейлора и Маклорена

Для приложений важно уметь данную функцию f(х) разлагать в степенной ряд, т. е. функцию f(х) представлять в виде суммы степенного ряда.

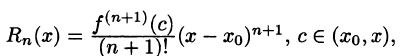
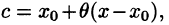
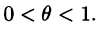
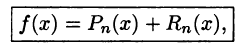
Как известно (см. теорема 26.1), для любой функции f(х), определенной в окрестности точки и имеющей в ней производные до (п + 1)-го порядка включительно, справедлива формула Тейлора:

где остаточный член в форме Лагранжа. Число с можно записать в виде где Формулу (64.1) кратко можно записать в виде

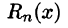
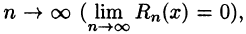
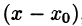
Если функция f(х) имеет производные любых порядков (т. е. бесконечно дифференцируема) в окрестности точки хо и остаточный член стремится к нулю при то из формулы Тейлора получается разложение функции f(х) по степеням , называемое рядом Тейлора:

Если в ряде Тейлора положить 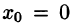, то получим разложение функции по степеням х в так называемый ряд Маклорена:

Отметим, что ряд Тейлора можно формально построить для любой бесконечно дифференцируемой функции (это необходимое условие) в окрестности точки . Но отсюда еще не следует, что он будет сходиться к данной функции f(x); он может оказаться расходящимся или сходиться, но не к функции f(x). Так, например, функция

имеет в точке х = 0 производные всех порядков, причем 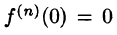при всяком п (см. пример 19.5). Ряд Маклорена имеет вид

Он сходится, но его сумма S(x) в любой точке х равна нулю, а не f(x).

Пусть для функции f(х) составлен соответствующий ей ряд Тейлора.

Теорема:

Для того чтобы ряд Тейлора (64.2) функции f(х) сходился к f(х) в точке х, необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора (64.1) стремился к нулю при 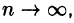т. е. чтобы

Пусть ряд Тейлора (64.2) сходится к функции f(х) в некоторой окрестности точки , т. е. Так как п-я частичная сумма ряда (64.2) совпадает с многочленом Тейлора , т. е. , находим:

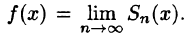
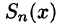
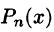
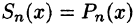
Обратно, пусть 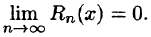Тогда

Замечание:

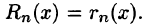
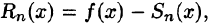
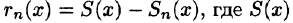
Если ряд Тейлора (64.2) сходится к порождающей функции f(х), то остаточный член формулы Тейлора равен остатку ряда Тейлора, т. е. (Напомним, что a — сумма ряда Тейлора.)

Таким образом, задача разложения функции f(х) в степенной ряд сведена по существу к определению значений х, при которых 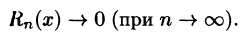Если сделать это не просто, то следует каким-нибудь иным способом убедиться, что написанный ряд Тейлора сходится к данной функции.

На практике часто пользуются следующей теоремой, которая дает простое достаточное условие разложимости функции в ряд Тейлора.

Теорема:

Если модули всех производных функций f(х) ограничены в окрестности точки одним и тем же числом М > 0, то для любого х из этой окрестности ряд Тейлора функции f(х) сходится к функции f(х), т. е. имеет место разложение (64.2).

Согласно теореме 64.1, достаточно показать, что

По условию теоремы 64.2 для любого п имеет место неравенство 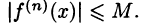Тогда имеем:

Осталось показать, что 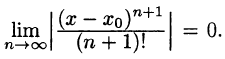Для этого рассмотрим ряд

то пo признаку Даламбера этот ряд сходится на всей числовой оси. Но тогда, в силу необходимого признака сходимости,

Следовательно,

Разложение некоторых элементарных функций в ряд Тейлора (Маклорена)

Для разложения функции f(х) в ряд Маклорена (64.3) нужно:

а) найти производные

б) вычислить значения производных в точке

в) написать ряд (64.3) для заданной функции и найти его интервал сходимости;

г) найти интервал (—R;R), в котором остаточный член ряда Маклорена 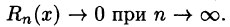Если такой интервал существует, то в нем функция f(х) и сумма ряда Маклорена совпадают.

Замечание:

В интервале сходимости степенного ряда остаточный член стремится к нулю при

Приведем таблицу, содержащую разложения в ряд Маклорена некоторых элементарных функций (эти разложения следует запомнить):

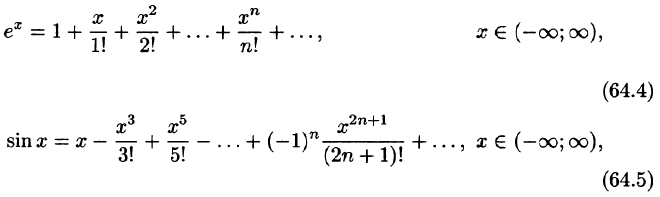
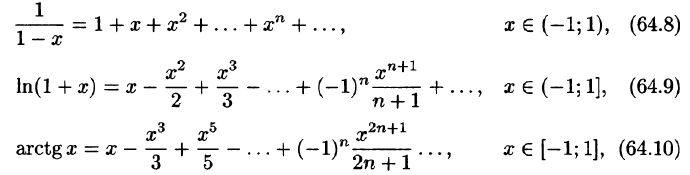
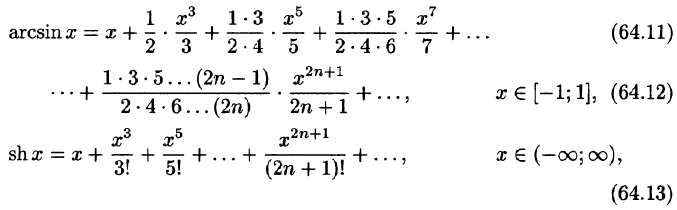
Докажем формулу (64.4). Пусть

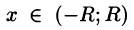
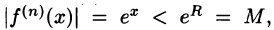
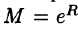
г) для всех имеем т.е. все производные в этом интервале ограничены одним и тем же числом .

Докажем формулу (64.5). Пусть

Легко проверить, что полученный ряд сходится на всей числовой оси, т. е. при всех

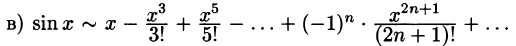
г) любая производная функции f(х) = sinx по модулю не превосходит единицы, 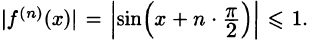Следовательно, по теореме 64.2 имеет место разложение (64.5).

Докажем формулу (64.6). Пусть

Формулу (64.6) можно доказать так же, как и формулу (64.5). Однако проще получить разложение функции cos х, воспользовавшись свойством 3 степенных рядов. Продифференцировав почленно ряд (64.5), получим:

Докажем формулы (64.13), (64.14). Пусть

Заменив в формуле (64.4) х на — х, получим разложение функции :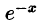

справедливое для всех

Суммируя (и вычитая) почленно равенства (64.4) и (64.15), получим разложение гиперболического косинуса (синуса):

Формулы (64.13) и (64.14) доказаны. ■

Докажем формулу (64.7). Пусть

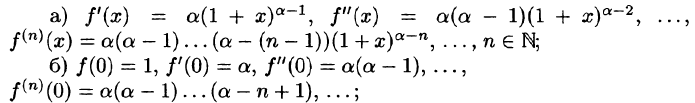
т. е. составленный для функции 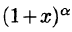ряд сходится в интервале (—1; 1).

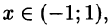
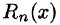
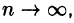
Можно показать, что и в данном случае, т.е. при остаточный член ) стремится к нулю при .

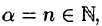
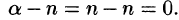
Ряд (64.7) называется биномиальным. Если то все члены ряда с (п + 1)-го номера равны 0, так как содержат множитель В этом случае ряд (64.7) представляет собой известную формулу бинома Ньютона:

Докажем формулу (64.8). Пусть

Формула (64.8) может быть получена разными способами:

1) пользуясь правилом разложения функции в ряд;

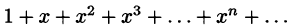
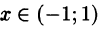
2) рассматривая ряд как ряд геометрической прогрессии, первый член которой равен единице и знаменатель q = х; известно (см. пример 62.1), что данный ряд сходится при и его сумма равна

3) воспользовавшись формулой (64.7): положив в ней 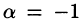и заменив х на -х, получим формулу (64.8).

Докажем формулу (64.9). Пусть 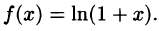Формула (64.9) также может быть доказана разными способами. Приведем один из них.

справедливое для всех 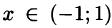. Используя свойство 4 степенных рядов, проинтегрируем данный ряд на отрезке

Можно показать, что это равенство справедливо и для х = 1. В

Докажем формулу (64.10). Пусть

Положив в формуле (64.7) а = —1 и заменив 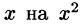, получим равенство

Можно показать, что равенство справедливо и при х = ±1, т. е. при всех х € [-1; 1].

Докажем формулу (64.12). Пусть

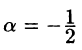
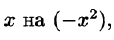
Положив в формуле (64.7) и заменив получим равенство

Можно показать, что полученное равенство справедливо при всех

Ряды (64.4)-(64.14) в комбинации с правилами сложения, вычитания, умножения, дифференцирования, интегрирования степенных рядов (см. свойства степенных рядов) могут быть использованы при разложении (некоторых) других функций в ряд Маклорена (Тейлора).

Пример:

Разложить в ряд Маклорена функцию

Решение:

Так как 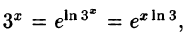то, заменяя х на xln3 в разложении (64.4), получим:

Пример:

Выписать ряд Маклорена функции

Решение:

то, воспользовавшись формулой (64.9), в которой заменим х на (— получим:

Пример:

Разложить в ряд Маклорена функцию

Решение:

Воспользуемся формулой (64.8). Так как

то, заменив 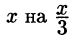в формуле (64.8), получим:

Некоторые приложения степенных рядов

Приближенное вычисление значений функции:

Пусть требуется вычислить значение функции f(х) при 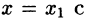заданной точностью

Если функцию f(х) в интервале (—R;R) можно разложить в степенной ряд

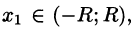
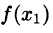
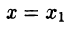
и то точное значение равно сумме этого ряда при , т. е.

а приближенное — частичной сумме 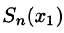, т.е.

Точность этого равенства увеличивается с ростом п. Абсолютная погрешность этого приближенного равенства равна модулю остатка ряда, т.е.

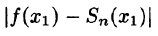
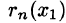
Таким образом, ошибку можно найти, оценив остаток ряда.

Для рядов лейбницевского типа

В остальных случаях (ряд знакопеременный или знакоположительный) составляют ряд из модулей членов ряда и для него стараются найти (подобрать) положительный ряд с большими членами (обычно это сходящийся ряд геометрической прогрессии), который легко бы суммировался. И в качестве оценки 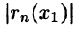берут величину остатка этого нового ряда.

Пример:

Найти sin 1 с точностью до 0,001.

Решение:

Согласно формуле (64.5),

Стоящий справа ряд сходится абсолютно (проверить самостоятельно). Так как

то для нахождения sin 1 с точностью до 0,001 достаточно первых трех слагаемых:

Допускаемая при этом ошибка меньше, чем первый отброшенный член (т.е. меньше, чем 0,0002). Вычисленное микрокалькулятором значение sin 1 примерно равно 0,84147.

Пример:

Вычислить число е с точностью до 0,001.

Решение:

Подставляя х = 1 в формулу (64.4), получим:

Справа стоит знакоположительный ряд. Возьмем п слагаемых и оценим ошибку

т.е. 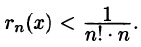Остается подобрать наименьшее натуральное число it, чтобы выполнялось неравенство

Нетрудно вычислить, что это неравенство выполняется при 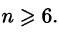Поэтому имеем:

Замечание:

Оценку остатка ряда можно производить с помощью остаточного члена ряда Маклорена

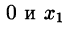
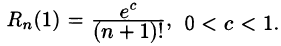
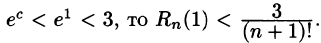
где с находится между . В последнем примере Так как При п = 6 имеем:

Приближенное вычисление определенных интегралов

Бесконечные ряды применяются также для приближенного вычисления неопределенных и определенных интегралов в случаях, когда первообразная не выражается в конечном виде через элементарные функции (см. § 34) либо нахождение первообразной сложно.

Пусть требуется вычислить 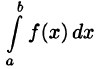с точностью до Если подынтегральную функцию f(x) можно разложить в ряд по степеням х и интервал сходимости (-R; R) включит в себя отрезок [а; b], то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда. Ошибку вычислений определяют так же, как и при вычислении значений функций.

Пример:

Вычислить интеграл 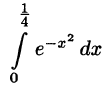с точностью до

Решение:

Разложим подынтегральную функцию в ряд Маклорена, заменяя 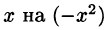в формуле (64.4):

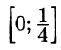
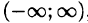
Интегрируя обе части равенства (65.1) на отрезке , лежащем внутри интервала сходимости , получим:

Получили ряд лейбницевского типа. Так как

то с точностью до 0,001 имеем:

Замечание:

Первообразную F(x) для функции 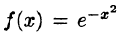легко найти в виде степенного ряда, проинтегрировав равенство (65.1) в пределах от 0 до х:

играют очень важную роль в теории вероятностей. Первая — плотность стандартного распределения вероятностей, вторая — функция Лапласа

(или интеграл вероятностей). Мы получили, что о функция Лапласа представляется рядом

который сходится на всей числовой оси.

Приближенное решение дифференциальных уравнений

Если решение дифференциального уравнения не выражается че-1>ез элементарные функции в конечном виде или способ его решения слишком сложен, то для приближенного решения уравнения можно воспользоваться рядом Тейлора.

Познакомимся с двумя способами решения дифференциальных уравнений с помощью степенных рядов.

Пусть, например, требуется решить уравнение

удовлетворяющее начальным условиям

Способ последовательного дифференцирования

Решение у = у(х) уравнения (65.2) ищем в виде ряда Тейлора:

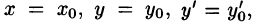
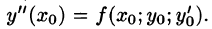
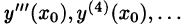
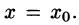
при этом первые два коэффициента находим из начальных условий (65.3). Подставив в уравнение (65.2) значения находим третий коэффициент: Значения находим путем последовательного дифференцирования уравнения (65.2) по х и вычисления производных при -Найденные значения производных (коэффициентов) подставляем в равенство (65.4). Ряд (65.4) представляет искомое частное решение уравнения (65.2) для тех значений х, при которых он сходится. Частичная сумма этого ряда будет приближенным решением дифференциального уравнения (65.2).

Рассмотренный способ применим и для построения общего решения уравнения (65.2), если 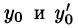рассматривать как произвольные постоянные.

Способ последовательного дифференцирования применим для решения дифференциальных уравнений любого порядка.

Пример:

Методом последовательного дифференцирования найти пять первых членов (отличных от нуля) разложения в ряд решения уравнения

Решение:

Будем искать решение уравнения в виде

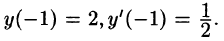
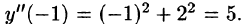
Здесь Находим у»(—1), подставив х = — 1 в исходное уравнение: Для нахождения последующих коэффициентов дифференцируем заданное дифференциальное уравнение:

При х = — 1 имеем:

Подставляя найденные значения производных в искомый ряд, получим:

Способ неопределенных коэффициентов

Этот способ приближенного решения наиболее удобен для интегрирования линейных дифференциальных уравнений с переменными коэффициентами.

Пусть, например, требуется решить уравнение

с начальными условиями

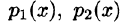
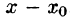
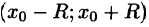
Предполагая, что коэффициенты и свободный член f(х) разлагаются в ряды по степеням , сходящиеся в некотором интервале , искомое решение у = у(х) ищем в виде степенного ряда

с неопределенными коэффициентами.

Коэффициенты 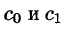определяются при помощи начальных условий

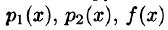
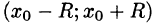
Для нахождения последующих коэффициентов дифференцируем ряд (65.6) два раза (каков порядок уравнения) и подставляем выражения для функции у и ее производных в уравнение (65.5), заменив в нем их разложениями. В результате получаем тождество, из которого методом неопределенных коэффициентов находим недостающие коэффициенты. Построенный ряд (65.6) сходится в том же интервале и служит решением уравнения (65.5).

Пример:

Найти решение уравнения

используя метод неопределенных коэффициентов.

Решение:

Разложим коэффициенты уравнения в степенные ряды:

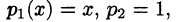
Ищем решение уравнения в виде ряда

Из начальных условий находим: 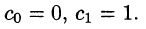Подставляем полученные ряды в дифференциальное уравнение:

Приравниваем коэффициенты при одинаковых степенях

Отсюда находим, что

Таким образом, получаем решение уравнения в виде

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник