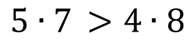Что такое сравнение значений выражений
Числовые и буквенные выражения
Числовые выражения
В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.
Значение выражения — это результат выполненных действий.
Чтение числовых выражений
Решение числовых выражений
45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13
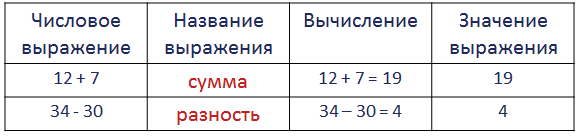
Сравнение значений числовых выражений
Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.
Для этого найдем значения каждого из них:
Буквенные выражения
Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.
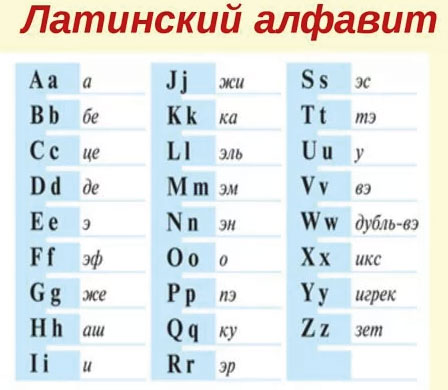
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.
Чаще всего используются буквы:
a, b, c, d, x, y, k, m, n
Алгоритм решения буквенного выражения
1. Прочитать буквенное выражение
2. Записать буквенное выражение
3. Подставить значение неизвестного в выражении
4. Вычислить результат
Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с
Подставим вместо неизвестного «с» число 4.
У нас получается выражение: 28 – 4
Переменные
Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства
Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:
Теперь мы можем найти значение этого выражения:
с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7
Поделись с друзьями в социальных сетях:
Математика. 2 класс
Конспект урока
Математика, 2 класс
Урок № 14. Числовые выражения. Порядок действий в числовых выражениях. Скобки. Сравнение числовых выражений
Перечень вопросов, рассматриваемых в теме:
— Что такое числовые выражения?
— Как правильно читать и записывать числовые выражения?
— Как выполнять порядок действий, если есть скобки?
— Как сравнить два выражения?
Числовое выражение – это запись, состоящая из чисел и знаков действий между ними.
Значение выражения – это результат выполненных действий.
Сравнить числовые выражения – найти значение каждого из выражений и их сравнить.
Порядок выполнения действий – это последовательность проводимых вычислений в данном выражении.
Основная и дополнительная литература по теме:
1. Моро М. И., Бантова М. А., Бельтюкова Г. В.и др. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1. –8-е изд. – М.: Просвещение, 2017. – с.38-40
2. Волкова А. Д. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций. М.: Просвещение, 2017, с. 22-27
3. Глаголева Ю. И., Волкова А. Д. Математика. КИМы. 2 кл: учебное пособие для общеобразовательных организаций. М.: Просвещение, Учлит, 2017, с.16
Теоретический материал для самостоятельного изучения
Маша и Миша решали пример: из числа 12 вычесть сумму чисел 7 и 3. Они записали его по-разному и получили разные ответы. Маша сначала из 12 вычла 7 и получила 5, потом прибавила 3, получила 8.
Миша обвёл овалом сумму чисел 7 и 3 и сначала посчитал сумму, получил 10. Затем от 12 отнял 10, получил 2.
Кто из них вычислил верно? Решил верно, Миша.
Запишем пример, который решали дети правильно:
Вычислим. 7 + 3 равно 10, из 12 вычесть 10, получится 2. Запомните: действия, записанные в скобках, выполняются первыми.
Посмотрим на запись.
Запись, в которой разные числа (однозначные и двузначные) соединены знаками «+» и «–» в различных сочетаниях, называется числовым выражением и читается так: «из числа 9 вычесть сумму чисел 6 и 2».
Найти значение выражения – это значит, нужно выполнить все указанные действия в выражении. Значение данного выражения 1.
Теперь мы будем называть примеры числовыми выражениями, а ответы значениями числовых выражений.
К числу 10 прибавить разность чисел 8 и 3.
Как найти значение выражения? Нужно выполнить необходимые действия. Но с какого действия нужно начинать? С того, которое записано в скобках. Находим разность чисел 8 и 3, будет 5, к 10 прибавить 5, получится 15.
Давайте сравним значения двух выражений:
Сначала найдем значение каждого из выражений и их сравним.
Виды числовых выражений в математике и их преобразование
Числовые выражения — что это такое
Выражения в математике определяют как запись утверждения с помощью чисел, букв алфавитов или переменных и знаков, которые обозначают действия.
Математические выражения бывают:
Маша решает 5 однотипных заданий за час. Сколько заданий может решить Маша за 2 часа?
Чтобы узнать, сколько заданий может решить Маша, нужно 5 заданий умножить на 2 часа усилий. Значит, 10 заданий Маша решит за два часа.
Числовые выражения записываются с помощью чисел.
Числовым выражением называется запись, которою составили с помощью чисел, арифметических знаков и скобок.
Число — это абстрактное выражения количества чего-либо. Не несет определяющей смысловой нагрузки о качественной характеристике объекта или предмета.
К арифметическим знакам относят — плюс, минус, деление, умножение.
Действия выполняются по арифметическим правилам слева направо. Сначала выполняют умножение / деление по порядку. После этого — сложение или вычитание.
Первыми выполняют действия в скобках, если они есть. При этом сохраняются правила «старшинства»: сначала умножение / деление, потом сложение / вычитание.
После выполнения действий в правильном порядке, получают число, которое называют значением числового выражения.
Значением числового выражения называют конечный результат вычисления.
Рассмотрим равенство 3+11=14.
3+11 — пример числового выражения.
Число 14 — значение выражения 3+11.
В случае, если в выражении встречается деление на нуль, то это выражение не имеет числового значения. На нуль делить нельзя. Такие выражения не имеют смысла.
Виды числовых выражений в математике и их преобразование
Преобразование числовых выражений заключается в выполнении действий, которые даны в выражении.
Действия выполняют согласно правилам, применимым в математической науке.
Правила или свойства преобразования выражений:
Порядок действий, сравнение и решение
Чтобы упростить числовое выражение, нужно:
Действуем по алгоритму и получаем:
1 действие — 3456-235 — считаем разность чисел 3456 и 235, записываем, сколько получится в скобках.
3 действие — находим частное двух чисел 45 и 9: 45:9.
4 действие — считаем разность двух чисел 547 и 345 — 547-345.
5 действие — к результату 4 действия прибавляем результат 2 действия.
6 действие — из числа, которое получили в пятом действии, вычитаем результат 3 действия.
7 действие — записываем ответ.
Найдите значение выражения: 4,37+15,4.
Значением данного выражения будет результат суммы чисел 4,37 и 15,4.
Чтобы сложить десятичные дроби, нужно уравнять количество знаков после запятой. В числе 4,37 — два знака после запятой, в 15,4 — один знак. Тогда дописываем нуль в 15,4. Получим дробь 15,40.
Считаем в столбик: записываем числа друг под другом — разряд под разрядом, запятая под запятой.
Числовые выражения можно сравнивать между собой.
Чтобы сравнить числовые выражения между собой:
Сравните выражения: 45+36 и 45-56.
Примеры для 7 класса, таблица
Упростите выражение: 21,97-17,88.
Чтобы найти разность десятичных дробей, нужно:
Уравниваем количество знаков после запятой в двух дробях. Записываем пример в столбик разряд под разрядом, запятая под запятой.
Чтобы умножить десятичную дробь на число, нужно:
При делении двух отрицательных чисел, получаем положительное число.
Чтобы разделить десятичную дробь на число:
Расставляем порядок действий. Первым действием будет произведение чисел 2,7 и 2. Вторым действием — сумма результата и 1,53.
Выполните действия: 3,73:3-0,75.
Первое действие — частное чисел 3,73 и 3. Находим значение данного выражения — 1,25.
Второе действие — от результата первого действия (1,25) отнимаем 0,75. Получаем 0,5.
Чтобы разделить два смешанных числа, нужно сначала их перевести в неправильные дроби.
Чтобы перевести смешанное число в неправильную дробь:
6 2 3 = 6 * 3 + 2 3 = 20 3
2 4 7 = 2 * 7 + 4 7 = 18 7
Записываем деление: 20 3 : 18 7
Чтобы разделить две обыкновенные дроби: первую дробь переписываем и умножаем на обратную второй дроби (перевернутую вторую).
20 3 : 18 7 = 20 * 7 3 * 18 = 10 * 7 3 * 9 = 70 27
Вся цепочка решения: 6 2 3 : 2 4 7 = 6 * 3 + 2 3 : 2 * 7 + 4 7 = 20 3 : 18 7 = 20 * 7 3 * 18 = 10 * 7 3 * 9 = 70 27 = 2 16 27
Запишите в виде выражения:
Сравнение значений выражений
Урок 3. Алгебра 7 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Сравнение значений выражений»
· разобрать, каким образом сравнивают выражения;
· показать что такое двойное неравенство;
· ввести понятия «строгое неравенство», «нестрогое неравенство».
Прежде, чем приступить к рассмотрению новой темы, вспомним, что:
Например, выражение 10(2 + 1,5) является числовым.
Выполнив действия этого числового выражения, соблюдая правильный порядок действий, получим число 35, которое называют значением данного числового выражения.
А теперь, чтобы разобраться, каким образом сравнивают значения выражений, решим следующую задачу.
Результат сравнения можно записать в виде следующего неравенства:
Таким образом, для любых двух числовых выражений можно установить, равны их значения или не равны. Если они не равны, то можем определить, какое из них больше и какое меньше.
Мы разобрались, как сравнить два числовых выражения. А как же быть с выражениями, содержащими переменные.
Давайте сравним значения выражений:
Видим, что для разных значений переменных результат сравнения выражений с переменными может оказаться различным.
Иногда перед нами может встать задача установить, между какими числами заключено значение выражения.
Сравнение значений выражений
Урок 3. Алгебра 7 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Сравнение значений выражений»
· разобрать, каким образом сравнивают выражения;
· показать что такое двойное неравенство;
· ввести понятия «строгое неравенство», «нестрогое неравенство».
Прежде, чем приступить к рассмотрению новой темы, вспомним, что:
Например, выражение 10(2 + 1,5) является числовым.
Выполнив действия этого числового выражения, соблюдая правильный порядок действий, получим число 35, которое называют значением данного числового выражения.
А теперь, чтобы разобраться, каким образом сравнивают значения выражений, решим следующую задачу.
Результат сравнения можно записать в виде следующего неравенства:
Таким образом, для любых двух числовых выражений можно установить, равны их значения или не равны. Если они не равны, то можем определить, какое из них больше и какое меньше.
Мы разобрались, как сравнить два числовых выражения. А как же быть с выражениями, содержащими переменные.
Давайте сравним значения выражений:
Видим, что для разных значений переменных результат сравнения выражений с переменными может оказаться различным.
Иногда перед нами может встать задача установить, между какими числами заключено значение выражения.